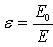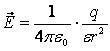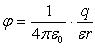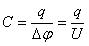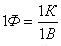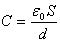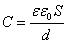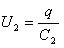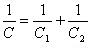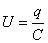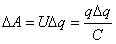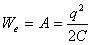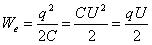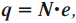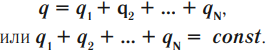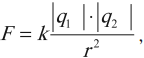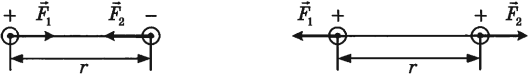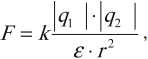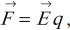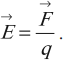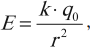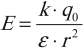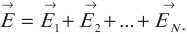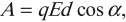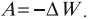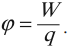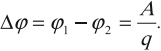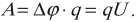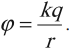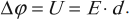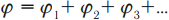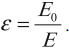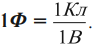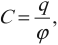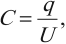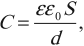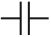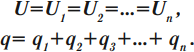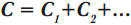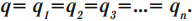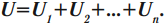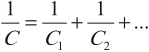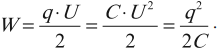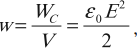внешнее электрическое поле это

2.3. Проводники во внешнем электрическом поле

При внесении незаряженного проводника во внешнее электрическое поле свободные заряды начинают двигаться и через небольшое время приходят в равновесие. Создается стационарное распределение зарядов, при котором на одной стороне проводника образуется избыток отрицательных зарядов, а на другой — избыток положительных. Это явление называется электростатической индукцией (рис. 2.5).

Рис. 2.5. Электростатическая индукция

Поле индуцированных (появившихся на поверхности проводника) зарядов полностью компенсирует внутри проводника внешнее поле. В противном случае внутри проводника происходило бы движение электри­ческих зарядов, и распределение не было бы стационарным. Итак, при равновесном состоянии суммарное поле (внешнее и индуцированных зарядов) внутри проводника равно нулю. Поэтому в отношении суммарного поля справедливы выводы, сделанные нами ранее для заряженных проводников в отсутствии внешнего поля.

В частности, электрическое поле будет отсутствовать во внутренней полости в материале проводника (рис. 2.6). На свойстве проводников экранировать внешние поля (не пропускать их внутрь области, окруженной проводником) основывается электростатическая защита от действия внешних электростатических полей (рис. 2.7).

Рис. 2.6. Появление индуцированных зарядов на поверхности проводника
при воздействии на него внешнего электрического поля

Рис. 2.7. Электростатическая защита. Поле в металлической полости равно нулю

Так, автомобиль является безопасным убежищем во время грозы, и не потому, что резина на колесах изолирует его от земли. Здесь мы должны быть благодарны теореме Остроградского — Гаусса. Однако следует подчеркнуть, что замкнутый полый проводник экранирует полость внутри себя только от внешних зарядов и полей. Если внести заряды внутрь полости, то там появится электрическое поле при том, что в самом проводнике поле, по-прежнему будет равно нулю.

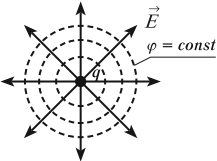
Далее, суммарное поле вблизи проводника перпендикулярно его поверхности и равно

где — плотность индуцированных зарядов (мы предполагаем, что про­водник в целом не заряжен).

На практике приходится решать следующую задачу. Дано некоторое внешнее поле. В него вносится проводник заданной формы. Надо найти распределение индуцированных на нем зарядов и те изменения суммарного поля вне проводника, к которым они приводят. Плотность зарядов при заданном потенциале проводника определяется кривизной поверхности: растет с увеличением положительной кривизны (выпуклости) и убывает с увеличением отрицательной кривизны (вогнутости) (рис. 2.8).

Рис. 2.8. Электрическое поле (силовые линии и эквипотенциальные поверхности)
незаряженной сферы вблизи точечного электрического заряда

Задача. Дана сферическая металлическая оболочка с внутренним и внешним радиусами и соответственно. В центр полости помещен заряд . Найти электрическое поле и потенциал системы, а также распределение зарядов на поверхности оболочки (рис. 2.9).

Рис. 2.9. Электрическое поле положительного заряда окруженного металлической оболочкой

Нам осталось найти потенциал поля в различных точках системы. Вне оболочки потенциал совпадает с потенциалом точечного заряда: На внешней поверхности оболочки потенциал ра­вен Поскольку внутри оболочки поля нет, потенциал сохраняет это значение во всех точках внутри металла. Вну­три полости потенциал опять совпадает с потенциалом точечного за­ряда. Поскольку последний определен с точностью до константы, имеем Значение этого потенциала на внутренней поверхности оболочки должно совпасть со значением потенциала на внешней оболочке. Отсюда можно найти постоянную

Графики зависимости напряженности поля и потенциала представлены на рис. 2.10.

Рис. 2.10. Напряженность и потенциал электрического поля заряда q,
окруженного металлической оболочкой с внутренним радиусом и внешним радиусом
Пунктирные линии соответствуют характеристикам поля одиночного заряда в отсутствие оболочки

Дополнительная информация

Источник

Как сказал.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Урок 26. Лекция 26. Проводники и диэлектрики в электрическом поле. Конденсаторы.

Мы знаем, что все вещества состоят из атомов, которые, в свою очередь, состоят из заряженных частиц. Если внешнее поле вокруг вещества отсутствует, то его частицы распределяются так, что суммарное электрическое поле внутри вещества равно нулю. Если вещество поместить во внешнее электрическое поле, то поле начет действовать на заряженные частицы и они перераспределяться так, что в веществе возникнет собственное электрическое поле. 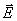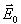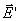Полное электрическое поле складывается из внешнего поля и внутреннего поля создаваемого заряженными частицами вещества.

Рассмотрим подробнее эти классы веществ.

Проводники в электрическом поле.

Проводниками называют вещества, проводящие электрический ток.

Типичными проводниками являются металлы.

Основная особенность проводников – наличие свободных зарядов ( в металлах это электроны), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.

В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды – индукционными зарядами.

Явление перераспределения зарядов внутри проводника под действием внешнего электрического поля называется электростатической индукцией.

Заряды, появляющиеся на поверхности проводника, называются индукционными зарядами.

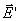
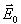
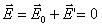
Индукционные заряды создают свое собственное поле , которое компенсирует внешнее поле во всем объеме проводника:

(внутри проводника).

Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника.

Диэлектрики в электрическом поле.

Диэлектриками (изоляторами) называют вещества, не проводящие электрического тока.

В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.

При внесении диэлектрика во внешнее электрическое поле 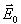в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.

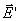
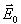
Связанные заряды создают электрическое поле , которое внутри диэлектрика направлено противоположно вектору напряженности внешнего поля . Этот процесс называется поляризацией диэлектрика.

Электрической поляризацией называют особое состояние вещества, при котором электрический момент некоторого объёма этого вещества не равен нулю.

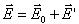
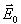
В результате полное электрическое поле внутри диэлектрика оказывается по модулю меньше внешнего поля .

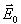
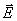
Физическая величина, равная отношению модуля напряженности внешнего электрического поля в вакууме к модулю напряженности полного поля в однородном диэлектрике , называется диэлектрической проницаемостью вещества.

Диэлектрическая проницаемость среды показывает, во сколько раз напряженность поля в вакууме больше, чем в диэлектрике. Это величина безразмерная (нет единиц измерения).

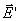
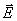
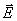
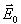
При поляризации неоднородного диэлектрика связанные заряды могут возникать не только на поверхностях, но и в объеме диэлектрика. В этом случае электрическое поле связанных зарядов и полное поле могут иметь сложную структуру, зависящую от геометрии диэлектрика. Утверждение о том, что электрическое поле в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем строго справедливо только в случае однородного диэлектрика, заполняющего все пространство, в котором создано внешнее поле. В частности:

Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд q, то напряженность поля 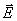, создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:

Если двум изолированным друг от друга проводникам сообщить заряды q₁ и q₂, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников.

Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U.

Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q₁ = – q₂ = q. В этом случае можно ввести понятие электрической емкости.

Электроемкостью (электрической емкостью) проводников называется физическая величина, характеризующая способность проводника или системы проводников накапливать электрический заряд.

Электроемкость находится как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

В системе СИ единица электроемкости называется фарад [Ф]:

Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – плоский конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния.

В целом ряде задач можно приближенно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.

Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:

Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы.

Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R₁ и R₂.

Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R₁ и R₂ и длины L.

Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:

— сферический конденсатор

— цилиндрический конденсатор

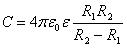
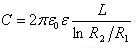
Для получения заданного значения емкости конденсаторы соединяются между собой, образуя батареи конденсаторов.

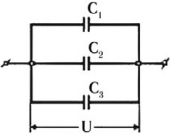
1) При параллельном соединении конденсаторов соединяются их одноименно заряженные обкладки.

Таким образом, при параллельном соединении электроемкости складываются.

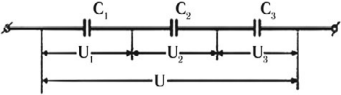
2) При последовательном соединении конденсаторов соединяют разноименно заряженные обкладки

Заряды обоих конденсаторов одинаковы q₁ = q₂ = q, напряжения на них равны 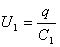и

Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U₁ + U₂.

Следовательно, 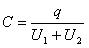или

При последовательном соединении конденсаторов складываются обратные величины емкостей.

Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.

Т.е. в случае n конденсаторов одинаковой емкости С емкость батареи

при параллельном соединении С_общ = nС

при последовательном соединении С_общ = С/n

Если обкладки заряженного конденсатора замкнуть металлическим проводником, то по цепи пойдет электрический ток, лампочка загорится и будет гореть до тех пор, пока конденсатор не разрядится. Значит, заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую.При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов

при переносе каждой порции Δq внешние силы должны совершить работу

Энергия W_e конденсатора емкости C, заряженного зарядом q, может быть найдена путем интегрирования этого выражения в пределах от 0 до q:

Электрическую энергию W_e следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля.

Источник

Электрическое поле и его характеристики

теория по физике 🧲 электростатика

Вокруг заряженных тел существует особая среда — электрическое поле. Именно это поле является посредником в передаче электрического взаимодействия.

Свойства электрического поля

Характеристики электрического поля

Напряженность численно равна электрической силе, действующей на единичный положительный заряд:

q 0 — пробный заряд.

Пример №1. Сила, действующая в поле на заряд в 20 мкКл, равна 4Н. Вычислить напряженность поля в этой точке.

20 мкКл = 20∙10 –6 Кл

Силовые линии — линии, касательные к которым совпадают с вектором напряженности.

Потенциальная энергия взаимодействия двух зарядов W (Дж) в вакууме:

Потенциальная энергия взаимодействия двух зарядов W (Дж) в среде:

Знак потенциальной энергии зависит от знаков заряженных тел:

Потенциал — энергетическая характеристика электрического поля. Обозначается как ϕ. Единица измерения — Вольт (В).

Численно потенциал равен отношению потенциальной энергии взаимодействия двух зарядов к единичному положительному заряду:

q 0 — пробный заряд.

Потенциал — скалярная физическая величина. Знак потенциала зависит от знака заряда, создающего поле. Отрицательный заряд создает отрицательный потенциал, и наоборот.

Значение потенциала зависит от выбора нулевого уровня для отсчета потенциальной энергии, а разность потенциалов — от выбора нулевого уровня не зависит.

Напряжение — разность потенциалов. Обозначается как U. Единица измерения — Вольт (В). Численно напряжение равно отношению работы электрических сил по перемещению заряда из точки 1 в точку 2:

Эквипотенциальные поверхности — поверхности, имеющие одинаковый потенциал. Они равноудалены от заряженных тел и обычно повторяют их форму. Эквипотенциальные поверхности перпендикулярны силовым линиям.

Пылинка, имеющая массу 10 −6 кг, влетела в однородное электрическое поле в направлении против его силовых линий с начальной скоростью 0,3 м/с и переместилась на расстояние 4 см. Каков заряд пылинки, если её скорость уменьшилась при этом на 0,2 м/с, а напряжённость поля 105 В/м?

Источник

Электрическое поле

Электродинамика – раздел физики, изучающий свойства и взаимодействия электрических зарядов, осуществляемые посредством электромагнитного поля.

Электростатикой называется раздел электродинамики, в котором рассматриваются свойства и взаимодействия неподвижных электрически заряженных тел или частиц.

Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макротелами.

Точечный заряд – заряженное тело, размер которого мал по сравнению с расстоянием, на котором оценивается его действие.

Электризация тел

Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.

Взаимодействие зарядов. Два вида зарядов

Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.

Обозначение – ​ \( q \) ​, единица измерения в СИ – кулон (Кл).

Величина заряда тела будет равна

Важно!
Частица может не иметь заряда, но заряд без частицы не существует.

Электрические заряды взаимодействуют:

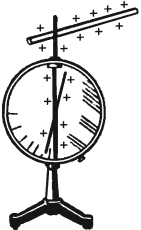
Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.

Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.

Закон сохранения электрического заряда

Систему называют замкнутой (электрически изолированной), если в ней не происходит обмена зарядами с окружающей средой.

В любой замкнутой (электрически изолированной) системе сумма электрических зарядов остается постоянной при любых взаимодействиях внутри нее.

Полный электрический заряд ​ \( (q) \) ​ системы равен алгебраической сумме ее положительных и отрицательных зарядов ​ \( (q_1, q_2 … q_N) \) ​:

Важно!
В природе не возникают и не исчезают заряды одного знака: положительный и отрицательный заряды могут взаимно нейтрализовать друг друга, если они равны по модулю.

Закон Кулона

Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.

Закон Кулона формулируется так:
сила взаимодействия ​ \( F \) ​ двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям ​ \( q_1 \) ​ и \( q_2 \) и обратно пропорциональна квадрату расстояния между ними ​ \( r \) ​:

где ​ \( k=\frac<1><4\pi\varepsilon_0>=9\cdot10^9 \) ​ (Н·м 2 )/Кл 2 – коэффициент пропорциональности,
​ \( \varepsilon_0=8.85\cdot10^ <-12>\) ​ Кл 2 /(Н·м 2 ) – электрическая постоянная.

Коэффициент ​ \( k \) ​ численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.

Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.

Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:

где ​ \( \varepsilon \) ​ – диэлектрическая проницаемость среды.

Закон Кулона применим к взаимодействию

В этом случае ​ \( r \) ​ – расстояние между центрами сферических поверхностей.

Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции).

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

где ​ \( \vec \) ​ – напряженность электрического поля, ​ \( q \) ​ – заряд.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

Напряженность электрического поля

Напряженность электрического поля ​ \( \vec \) ​ – векторная физическая величина, равная отношению силы ​ \( F \) ​, действующей на пробный точечный заряд, к величине этого заряда ​ \( q \) ​:

Напряженность поля точечного заряда в вакууме вычисляется по формуле:

Напряженность поля точечного заряда в среде вычисляется по формуле:

где ​ \( \varepsilon \) ​ – диэлектрическая проницаемость среды.

Важно!
Напряженность электрического поля не зависит от величины пробного заряда, она определяется величиной заряда, создающего поле.

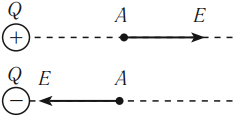
Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку.

Линией напряженности электрического поля называется линия, касательная к которой в каждой точке направлена вдоль вектора напряженности ​ \( \vec \) ​.

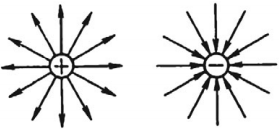
Линии напряженности электростатического поля начинаются на положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность от положительного заряда и приходят из бесконечности к отрицательному заряду.

Распределение линий напряженности вокруг положительного и отрицательного точечных зарядов показано на рисунке.

Определяя направление вектора ​ \( \vec \) ​ в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.

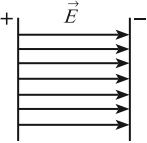
Поле, в котором напряженность одинакова по модулю и направлению в любой точке, называется однородным электрическим полем. Однородным можно считать электрическое поле между двумя разноименно заряженными металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу.

Принцип суперпозиции электрических полей

Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов.

Принцип суперпозиции электрических полей: напряженность электрического поля системы ​ \( N \) ​ зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности:

Электрические поля от разных источников существуют в одной точке пространства и действуют на заряд независимо друг от друга.

Потенциальность электростатического поля

Электрическое поле с напряженностью ​ \( \vec \) ​ при перемещении заряда ​ \( q \) ​ совершает работу. Работа ​ \( A \) ​ электростатического поля вычисляется по формуле:

где ​ \( d \) ​ – расстояние, на которое перемещается заряд,
​ \( \alpha \) ​ – угол между векторами напряженности электрического поля и перемещения заряда.

Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле.

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным.

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ​ \( W \) ​, так как буквой ​ \( E \) ​ обозначают напряженность поля:

Потенциальная энергия заряда ​ \( q \) ​, помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – ​ \( \varphi \) ​, единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – ​ \( \Delta\varphi \) ​, единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой ​ \( U \) ​ и называют напряжением.

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле.

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда ​ \( q \) ​ в точке, удаленной от него на расстояние ​ \( r \) ​, вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (​ \( r =R \) ​, где ​ \( R \) ​ – радиус шара). Напряженность поля внутри шара равна нулю.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

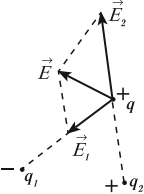
Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

Проводники в электрическом поле

Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.

Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.

Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.

Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.

Важно!
Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей. На этом основана электростатическая защита.

Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.

Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.

Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны).

Диэлектрики в электрическом поле

Диэлектриками называют вещества, не проводящие электрический ток. Диэлектриками являются стекло, фарфор, резина, дистиллированная вода, газы.

В диэлектриках нет свободных зарядов, все заряды связаны. В молекуле диэлектрика суммарный отрицательный заряд электронов равен положительному заряду ядра. Различают полярные и неполярные диэлектрики.

В молекулах полярных диэлектриков ядра и электроны расположены так, что центры масс положительных и отрицательных зарядов не совпадают и находятся на некотором расстоянии друг от друга. То есть молекулы представляют собой диполи независимо от наличия внешнего электрического поля. В отсутствие внешнего электрического поля из-за теплового движения молекул диполи расположены хаотично, поэтому суммарная напряженность поля всех диполей диэлектрика равна нулю.

Если в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов в молекуле диэлектрика совпадают, то он называется неполярным. Пример такого диэлектрика – молекула водорода. Если такой диэлектрик поместить во внешнее электрическое поле, то направления векторов сил, действующих на положительные и отрицательные заряды, будут противоположными. В результате молекула деформируется и превращается в диполь. При внесении диэлектрика в электрическое поле происходит его поляризация.

Поляризация диэлектрика – процесс смещения в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества в электрическом поле.

Если диэлектрик неполярный, то в его молекулах происходит смещение положительных и отрицательных зарядов. На поверхности диэлектрика появятся поверхностные связанные заряды. Связанными эти заряды называют потому, что они не могут свободно перемещаться отдельно друг от друга.

Внутри диэлектрика суммарный заряд равен нулю, а на поверхностях заряды не скомпенсированы и создают внутри диэлектрика поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Это значит, что внутри диэлектрика поле имеет меньшую напряженность, чем в вакууме.

Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:

В полярном диэлектрике во внешнем электрическом поле происходит поворот диполей, и они выстраиваются вдоль линий напряженности.

Если внесенный в электрическое поле диэлектрик разрезать, то его части будут электрически нейтральны.

Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – ​ \( C \) ​, единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

Формула для вычисления электроемкости:

где ​ \( q \) ​ – заряд проводника, ​ \( \varphi \) ​ – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

где ​ \( q \) ​ – модуль заряда одной из обкладок,
​ \( U \) ​ – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью ​ \( S \) ​, находящиеся на расстоянии ​ \( d \) ​ друг от друга.

Электроемкость плоского конденсатора:

где ​ \( \varepsilon \) ​ – диэлектрическая проницаемость вещества между обкладками,
\( \varepsilon_0 \) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

Величина, обратная общей емкости:

При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости.

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Энергия электрического поля конденсатора

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:

Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.

Плотность энергии электрического поля:

где ​ \( V \) ​ – объем пространства между обкладками конденсатора.

Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.

Источник