линия ската что такое

Линия ската что такое

Среди прямых линий, принадлежащих плоскости, особое значение имеют прямые, занимающие частное положение в пространстве:

а) модель		б) эпюр
Рисунок 55. Горизонталь

4. Прямые, принадлежащие плоскости и образующие с плоскостью проекций наибольший угол называются линиями наибольшего наклона данной плоскости к плоскости проекций. С помощью линий наибольшего наклона определяют двугранные углы между заданной плоскостью и соответствующей плоскостью проекций.

Прямые плоскости, перпендикулярные соответствующим линиям уровня являются линиями наибольшего наклона.

Линия наибольшего наклона к горизонтальной плоскости проекций называется линией ската . Такое название объясняется тем, что эта линия является траекторией, по которой шарик скатывается с данной плоскости. По отношению к плоскостям П ₂ и П₃ целесообразнее употреблять название линия наибольшего наклона.

Источник

Написать отчет по практике

Линия ската и углы наклона плоскости к плоскостям проекций

Линией наибольшего ската (уклона) называется прямая плоскости, перпендикулярная к горизонтальному следу или горизонталям этой плоскости. (рис. 6.7, а,б, а также см. тему 3). При помощи линий ската определяется угол наклона данной плоскости к плоскости H.

Аналогично могут быть определены углы наклона плоскости и к плоскостям V и W. Для этого используются прямые наибольшего уклона данной плоскости к соответствующим плоскостям проекций.

Прямые наибольшего уклона, перпендикулярные фронталям плоскости, образуют наибольший угол с фронтальной плоскостью;

прямые наибольшего уклона, перпендикулярные профильным прямым плоскости, образуют наибольший угол с профильной плоскостью проекций.

Угол, образованный между прямой наибольшего уклона и ее проекцией на выбранную плоскость проекций, определяют угол наклона плоскости общего положения к плоскостям проекций. На эпюре данный угол может быть определен из метода прямоугольного треугольника. Перечень обязательных элементов и предшествующих им разделительных знаков должен строго соответствовать приведенным ниже требованиям. Перечень факультативных элементов определяется автором текстового документа. В него можно включать и такие источники, с которыми автор рекомендует познакомиться для более глубокого изучения рассматриваемого в документе вопроса. При библиографических описаниях необходимо строго соблюдать установленные стандартом разделительные знаки.

Источник

Линия наибольшего наклона

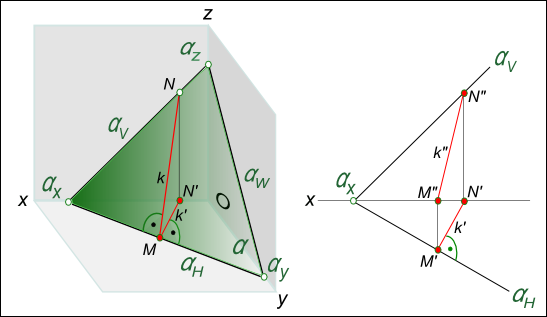
Отличительным признаком для проекции линии наибольшего ската является перпендикулярность ее горизонтальной проекции, горизонтальной проекции горизонтали и горизонтальному следу плоскости α_H см. рисунок. Следует иметь ввиду, что линия наибольшего наклона будет использоваться в дальнейшем для определения угла наклона плоскости к плоскостям проекции.

Действительно, линия наибольшего наклона k и ее горизонтальная проекция k` образуют линейный угол NMN` (NM⊥α_H и N`M⊥α_H), который служит мерой двугранного угла, составленного плоскостями α и H.

Для линии наибольшего наклона плоскости к V характерно, что ее фронтальная проекция, перпендикулярна к фронтальной проекции фронтали (или α_V) и, наконец, профильная проекция линии наибольшего наклона плоскости к W займет положение, перпендикулярное к профильной проекции профильной прямой (или α_W).

Линия наибольшего наклона k к плоскости H строится начиная с ее горизонтальной проекции k`.

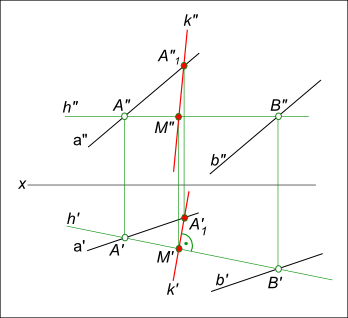
Линия наибольшего наклона должна быть построена дважды в задаче на определение углов наклона плоскости или грани a//b к горизонтальной и фронтальной плоскостям проекции

Построенные линия наибольшего наклона k и линия наибольшего наклона n представляют собой прямые общего положения, смотри:
Прямая общего положения;
Углы наклона прямой.

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

4.6. Линия наибольшего наклона (ската)

К группе главных линий плоскости относится прямая, принадлежащая плоскости и перпендикулярная линиям уровня этой плоскости – горизонтали, фронтали или профильной прямой и (или) соответствующим следам плоскости. Эта линия получила название линии наибольшего наклона заданной плоскости к плоскостям проекций П1, П2, П3. Иногда линию наибольшего наклона к плоскости называют линией ската.

Следует иметь ввиду, что линия наибольшего наклона может использоваться для определения угла наклона заданной плоскости к плоскостям проекций.

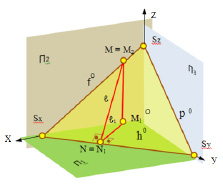
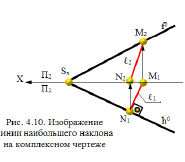
Если рассматривать такую линию ℓ в пространстве (рис. 4.9), то можно сделать вывод о том, что линия наибольшего наклона ℓ и ее горизонтальная проекция ℓ1 образуют линейный угол MNM1 (MN ⊥ h0 и M1N ⊥ h0), который служит мерой двугранного угла, составленного горизонтальной и заданной плоскостями.

Рис. 4.9. Изображение линии наибольшего наклона плоскости

На комплексном чертеже в двух плоскостях проекций (рис. 4.10) изображение линии наибольшего наклона изображается с учётом двух её проекций ℓ (ℓ1,ℓ2).

На комплексном чертеже для линии наибольшего наклона заданной плоскости к горизонтальной плоскости проекций характерно, что её горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали h этой плоскости.

При наклоне к фронтальной плоскости проекций, фронтальная проекция линии наибольшего наклона перпендикулярна к фронтальной проекции фронтали f этой плоскости и, наконец, профильная проекция линии наибольшего наклона плоскости к профильной плоскости проекций займет положение, перпендикулярное к профильной проекции профильной прямой p.

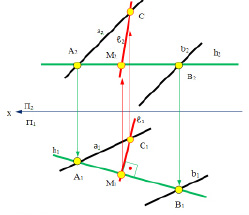
Рассмотрим (рис. 4.11) пример построения линии наибольшего наклона (ЛНН) ℓ плоскости α (a || b) к горизонтальной плоскости проекций П1.

Построение линии наибольшего наклона плоскости ℓ на комплексном чертеже начинается с построения её горизонтальной проекции ℓ1.

На рисунке показана линия наибольшего наклона плоскости α (a ║ b) к горизонтальной плоскости проекций П1 – прямая ℓ.

Рассмотрим алгоритм нахождения линии наибольшего наклона плоскости α(a ║ b) к одной из плоскостей проекций на комплексном чертеже.

Рис. 4.11. Изображение линии наибольшего наклона плоскости α (a ║ b)
к горизонтальной плоскости проекций П1

Прежде чем провести горизонтальную проекцию ℓ1, определяем направление горизонтальной проекции горизонтали h1:

— проводим произвольную фронтальную проекцию h2(h2║x);

— отмечаем точки A2=h2∩a2 и B2=h2∩b2;

— по A2 и B2 находим A1 и B1, которые определяют положение h1.

— через произвольную точку С1 плоскости α проводим ℓ1 (ℓ ⊥ h1);

— отмечаем M1 = ℓ1∩ h1;

— по С1 и M1 находим С2 и M2;

— соединив эти две точки, определим положение фронтальной проекции прямой ℓ2 – линии наибольшего наклона плоскости α (a ║ b) к горизонтальной плоскости проекций П1.

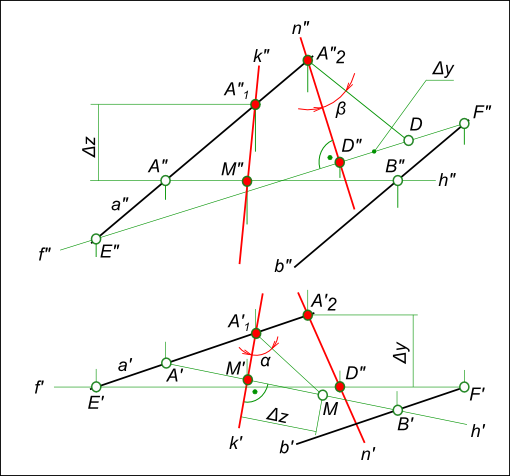
Обращаясь к рис. 4.9. можно сделать вывод, что для определения углов α° и β° наклона плоскости a ║ b к горизонтальной П1 и фронтальной П2 плоскостям проекции линия наибольшего наклона плоскости должна быть построена в этой плоскости дважды – к горизонтали этой плоскости h и фронтали f.

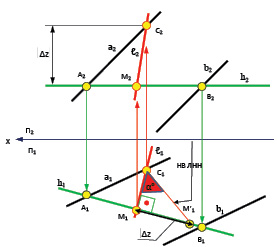
Из рисунка видно, что угол наклона α° определяется из прямоугольного треугольника МNM1, в котором гипотенуза MN является натуральной величиной линии наибольшего наклона плоскости, а угол α° является углом между натуральной величиной ℓ и её проекцией ℓ1 на горизонтальной плоскости проекций П1. Следовательно, при определении угла наклона плоскости α (a ║ b) на комплексном чертеже необходимо после построений (рис. 4.11), определивших направление линии наибольшего наклона к П1, определить натуральную величину известного отрезка М1С1 (рис. 4.12).

Рис. 4.12. Определение угла наклона плоскости
к горизонтальной плоскости проекций

Для этого необходимо воспользоваться правилом прямоугольного треугольника и построить прямоугольный треугольник на двух катетах, один из которых – это отрезок М1С1, а величину второго катета Δz определить во фронтальной плоскости проекций П2 как разницу начала и конца отрезка М2С2. Величину Δz отложить под прямым углом к М1С1 и получить точку М’1, которую соединить с точкой С1. Линия М’1С1 – натуральная величина отрезка М1С1 = ℓ1. Значит найдена натуральная величина линии наибольшего наклона заданной плоскости (НВ ЛНН) к горизонтальной плоскости проекций П1. Согласно правилу прямоугольного треугольника известно, что в построенном прямоугольном треугольнике угол между гипотенузой (натуральной величиной отрезка) и проекцией отрезка является углом наклона к плоскости проекций. Значит, в нашем случае (рис. 4.12) получена величина угла наклона (α°) заданной плоскости α (a ║ b) к горизонтальной плоскости проекций П1.

Для определения угла наклона β° заданной плоскости к фронтальной плоскости проекций П2 следует выполнить на комплексном чертеже действия аналогичные действиям при определении α°.

Разница в определении состоит в том, что построение начинается с определения фронтали f заданной плоскости.

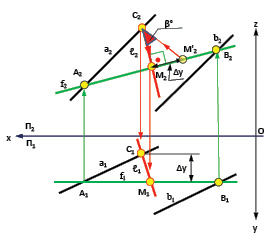
Рассмотрим (рис. 4.13) плоскость, заданную двумя параллельными прямыми α (a ║ b) и выполним построения линии наибольшего наклона в заданной плоскости для нахождения угла наклона этой плоскости к фронтальной плоскости проекций П2.

Рис. 4.13. Определение угла наклона плоскости к фронтальной плоскости проекций

Угол α° – это угол наклона прямой ℓ к горизонтальной плоскости проекций П1. Он соответствует углу наклона плоскости α (a ║ b) к той же плоскости проекций П1.

Угол β° – это угол наклона прямой ℓ к фронтальной плоскости проекций П2. Он соответствует углу наклона плоскости α (a ║ b) к той же плоскости проекций П2.

Вопросы для самоконтроля

1. Каковы условия перпендикулярности прямых линий на комплексном чертеже?

2. Каковы условия перпендикулярности прямой к плоскости на комплексном чертеже.

3. Какова сущность способа прямоугольного треугольника?

4. Какое свойство линии наибольшего наклона является основным?

5. Как можно определить действительную величину отрезка, находящегося в общем положении по отношению к плоскостям проекций?

6. Как определяется угол наклона плоскости к плоскостям проекцийс помощью линий наибольшего наклона?

Источник

Статьи о радиотехнике, технологиях, чертежах, 3D-моделировании

Публикации для людей, интересующихся наукой и техникой

ПЛОСКОСТЬ – является простейшей поверхностью, которую можно представить, например, как веер линий, полученных при движении прямой, закрепленный в некоторой (.), по другой прямой

В отличие от линии, плоскость не может быть задана на чертеже своими проекциями. Плоскость в пространстве безгранична, бесконечна, а потому проекции её (.) займут всё поле чертежа. Положение плоскости в пространстве определяется положением задающихся ее элементов, входящих в определитель плоскости, т.е. плоскость задается проекциями геометрических объектов, располагающихся на ее поверхности. Графически плоскость может быть задана одним из шести способов:

От любого из этих способов можно легко перейти к любому другому.

СЛЕДЫ ПЛОСКОСТИ (сп) – пл, по которой данная плоскость пересекается с горизонтальной, фронтальной или профильной пп. В зависимости от того, какую пп данная плоскость пересекает, различают: фронтальный, горизонтальный и профильный следы плоскости. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие – разноименные проекции – оказываются лежащими на осях координат. Проекции следов, совпадающие с осями координат, обозначать не принято. Любые два следа плоскости, как две пересекающиеся прямые, вполне определяют положение плоскости в пространстве. Третий след плоскости всегда можно построить по двум данным. След плоскости как линия в системе пп является линией нулевого уровня, т.к. принадлежит поверхности какой-либо плоскости проекций.

ТОЧКИ СХОДА СЛЕДОВ (тсс) – точки пересечения следов заданной плоскости с координатными осями X, Y и Z. Обозначаются, например, для плоскости α соответственно αx, αy, αz.

ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ (поп) – это плоскость, занимающая произвольное положение относительно плоскостей проекций, т.е. она не ⟂ и не ∥ ни одной основной плоскости проекций. Ни одна из ортогональных проекций геометрических объектов, задающих плоскость общего положения, не сливается в пл. Метрические характеристики такой плоскости на чертеже искажаются и не могут быть определены непосредственно с чертежа плоскости. Различают: восходящие и нисходящие плоскости общего положения.

ВОСХОДЯЩАЯ ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ (впоп) – плоскость произвольного положения, которая, удаляясь от наблюдателя, идет вверх (на подъем). Метрические характеристики данной плоскости на чертеже напрямую не определяются. Угол наклона такой плоскости можно получить с использованием линии ската.

НИСХОДЯЩАЯ ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ (нпоп) – плоскость произвольного положения, которая, удаляясь от наблюдателя, идет вниз (на спуск). Метрические характеристики данной плоскости на чертеже напрямую не определяются. Угол наклона такой плоскости можно получить с использованием линии ската.

ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ (пчп) – это плоскости, ⟂ либо ∥ пп. Различают: проецирующие плоскости и плоскости уровня. На ортогональном чертеже любой плоскости частного положения хотя бы одна проекция всегда вырождается в пл.

ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ (пп) – это плоскость, ⟂ к одной из пп и при этом не ⟂ и не ∥ двум другим. В зависимости от того к какой плоскости проекций ⟂ проецирующая плоскость, различают: горизонтально проецирующую, фронтально проецирующую и профильно проецирующую плоскости.

ГОРИЗОНТАЛЬНО ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ (гпп) – плоскость, ⟂ горизонтальной плоскости проекций П₁ и при этом не ⟂ и не ∥ фронтальной П₂ и профильной П₃ плоскостям проекций. Гпп представляет собой прямую линию, которая одновременно является гcп. Любой геометрический объект, расположенный в этой плоскости, проецируется на горизонтальной плоскости проекций П₁ в эту прямую. Угол, который составляет гсп с координатной осью Х, равен углу наклона этой плоскости к фронтальной плоскости проекций П₂, а с координатной осью Y– к профильной плоскости проекций П₃. Фронтальный след гпп ⟂ оси координат X.

ФРОНТАЛЬНО ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ (фпп) – плоскость, ⟂ фронтальной плоскости проекций П₂ и при этом не ⟂ и не ∥ горизонтальной П₁ и профильной П₃ плоскостям проекций. Фпп представляет собой прямую линию, которая одновременно является фсп. Любой геометрической объект, лежащий в этой плоскости, на чертеже совмещен с ее фронтальным следом. Угол, который составляет фсп с координатной осью Х, равен наклону данной плоскости к горизонтальной плоскости проекций П₁, а с координатной осью Z – к профильной плоскости проекций П₃. Горизонтальный след фронтально проецирующей плоскости перпендикулярен оси координат Х.

ПРОФИЛЬНО ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ (ппп) – плоскость, ⟂ профильной плоскости проекций П₃ и при этом не ⟂ и не ∥ горизонтальной П₁ и фронтальной П₂ плоскостям проекций. Ппп представляет собой прямую линию, которая одновременно является профильным следом плоскости. Любой геометрический объект, лежащий в этой плоскости, на чертеже совмещен с ее профильным следом. Угол, который составляет псп с координатной осью Y, равен наклону данной плоскости к горизонтальной плоскости проекций П₁, а с координатной осью Z – к фронтальной плоскости проекций П₂. Горизонтальный след такой плоскости перпендикулярен оси Y. В зависимости от удаления от наблюдателя различают: восходящую профильно проецирующую и нисходящую ппп.

ПЛОСКОСТЬ УРОВНЯ (пу) – это плоскость ∥ одной из плоскостей проекций, а значит ⟂ одновременно к двум другим плоскостям проекций. В зависимости от того какой плоскости проекций параллельна данная плоскость, различают: горизонтальную, фронтальную и профильную плоскости уровня. Любой геометрический объект, расположенный в плоскости уровня, в зависимости от параллельности проецирует на одну из плоскостей проекций в натуральную величину.

ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ (гпу) – плоскость, ∥ гпп П₁ и при этом ⟂ фронтальной П₂ и профильной П₃ плоскостям проекций. Фронтальная и профильная проекции такой плоскости – прямые линии, совпадающие с одноименными следами этой плоскости, и ∥ осям координат X и Y соответственно. Любой геометрический объект, расположенный в гпу, проецируется без искажения на гпп П₁.

ФРОНТАЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ (фпу) – плоскость, ∥ фронтальной плоскости проекций П₂ и при этом ⟂ горизонтальной П₁ и профильной П₃ плоскостям проекций. Горизонтальная и профильная проекции такой плоскости – прямые линии, совпадающие с одноименными следами этой плоскости и ∥ осям координат Х и Z соответственно. Любой геометрический объект, расположенный во фпу, проецируется без искажения на фронтальную плоскость проекций П₂.

ПРОФИЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ (ппу) – плоскость, ∥ профильной плоскости проекций П₃ и при этом ⟂ горизонтальной П₁ и фронтальной П₂ плоскостям проекций. Горизонтальная и фронтальная проекции такой плоскости – прямые линии, совпадающие с одноименными следами этой плоскости и ∥ осям координат Y и Z соответственно. Любой геометрический объект, расположенный в ппу, проецируется без искажения на ппп П₃.

ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ (глп) – это пл, расположенные в данной плоскости, выделяемые среди множества других линий, как занимающие особое положение. Это линии уровня плоскости: горизонталь h, фронталь f и ппп p, а также линии наибольшего наклона плоскости к плоскостям проекций П₁, П₂ и П₃.

ГОРИЗОНТАЛЬ ПЛОСКОСТИ (гп) – пл, принадлежащая этой плоскости и ∥ гпп П₁, т.е. это горизонтальная прямая линия уровня, лежащая на поверхности какой-либо плоскости. Фронтальная и профильная проекции горизонтали плоскости ∥ осям координат X и Y соответственно Все горизонтали плоскости ∥ друг другу и горизонтальному следу своей плоскости. Обозначается на чертеже буквой – h.

ФРОНТАЛЬ ПЛОСКОСТИ (фп) – пл, принадлежащая этой плоскости и ∥ фпп П₂, т.е. это фронтальная прямая линия уровня, лежащая на поверхности какой-либо плоскости. Горизонтальная и профильная проекции фронтали плоскости ∥ осям координат X и Z соответственно. Все фронтали плоскости параллельны друг другу и фронтальному следу своей плоскости. Обозначается на чертеже буквой – f.

ПРОФИЛЬНАЯ ПРЯМАЯ ЛИНИЯ ПЛОСКОСТИ (пплп) – пл, принадлежащая этой плоскости и параллельная профильной плоскости проекций П₃, т.е. это профильная прямая линия уровня, лежащая на поверхности какой-либо плоскости. Фронтальная и горизонтальная проекции профильной прямой плоскости параллельны осям координат Z и Y соответственно. Все профильные прямые линии плоскости параллельны друг другу и профильному следу своей плоскости. Обозначается на чертеже буквой – p.

ЛИНИИ НУЛЕВОГО УРОВНЯ ПЛОСКОСТИ (лнуп) – это пл, принадлежащие одновременно данной плоскости и какой-либо плоскости проекций, т.е. являются одновременно и главными линиями плоскости, и следами этой плоскости. Горизонтальный след плоскости – это горизонталь плоскости нулевого уровня, фронтальный след плоскости – фронталь плоскости нулевого уровня и профильный след плоскости – профильная прямая плоскости нулевого уровня. Обозначаются на чертеже – h_оά, f_оά, ρ_оά соответственно.

ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ (лннп) к плоскостям проекций П₁, П₂ и П₃ – пл, лежащие в ней и ⟂ или к горизонталям плоскости, или к ее фронталям, или к ее профильным прямым.

ЛИНИЯ СКАТА ПЛОСКОСТИ (лсп) – линия наибольшего наклона плоскости к гпп П₁, т.е. пл, проведенная по поверхности плоскости ⟂ любой горизонтали этой плоскости. Согласно теореме о проекции прямого угла, прямой угол между горизонталью плоскости и линией ската плоскости проецируется на гпп П₁ без искажения. Лсп и ее горизонтальная проекция образуют линейный угол, которым измеряется двугранный, составленный данной плоскостью и пп П₁.

ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ К ФРОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ П₂ (лннпкфпп) – пл, проведенная по поверхности какой-либо плоскости ⟂ любой фронтали этой плоскости. Согласно теореме о проекции прямого угла, прямой угол между лннпкфпп П₂ и фронталью этой плоскости проецируется на фронтальную плоскость проекций П₂ без искажения.

ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ К ПРОФИЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ П₃ (лннпкппп) – пл, проведенная по поверхности плоскости перпендикулярно профильной прямой линии уровня этой плоскости. Согласно теореме о проекции прямого угла, прямой угол между лннпкппп П₃ и профильной прямой линией этой плоскости проецируется на профильную плоскость проекций П₃ без искажения.

Если у вас остались вопросы или предложения по данной статье, направляйте ваш материал к нам на контакты.

Источник