Как построить распределение по данным
Группировка данных и построение ряда распределения
Виды статистических группировок
Принципы построения статистических группировок
При использовании персональных компьютеров для обработки статистических данных группировка единиц объекта производится с помощью стандартных процедур.
Одна из таких процедур основана на использовании формулы Стерджесса для определения оптимального числа групп:
Длину частичных интервалов вычисляют как h=(xmax-xmin)/k
Построить вариационный ряд. По найденному ряду построить полигон распределения, гистограмму, кумуляту. Определить моду и медиану.
Скачать решение
Пример. По результатам выборочного наблюдения (выборка А приложение):
а) составьте вариационный ряд;
б) вычислите относительные частоты и накопленные относительные частоты;
в) постройте полигон;
г) составьте эмпирическую функцию распределения;
д) постройте график эмпирической функции распределения;
е) вычислите числовые характеристики: среднее арифметическое, дисперсию, среднее квадратическое отклонение. Решение
Требуется: ранжировать ряд, построить интервальный ряд распределения, вычислить среднее значение, колеблемость среднего значения, моду и медиану для ранжированного и интервального рядов.
На основе исходных данных построить дискретный вариационный ряд; представить его в виде статистической таблицы и статистических графиков. 2). На основе исходных данных построить интервальный вариационный ряд с равными интервалами. Число интервалов выбрать самостоятельно и объяснить этот выбор. Представить полученный вариационный ряд в виде статистической таблицы и статистических графиков. Указать виды примененных таблиц и графиков.
С целью определения средней продолжительности обслуживания клиентов в пенсионном фонде, число клиентов которого очень велико, по схеме собственно-случайной бесповторной выборки проведено обследование 100 клиентов. Результаты обследования представлены в таблице. Найти:
а) границы, в которых с вероятностью 0.9946 заключено среднее время обслуживания всех клиентов пенсионного фонда;
б) вероятность того, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине);
в) объем повторной выборки, при котором с вероятностью 0.9907 можно утверждать, что доля всех клиентов фонда с продолжительностью обслуживания менее 6 минут отличается от доли таких клиентов в выборке не более чем на 10% (по абсолютной величине).
2. По данным задачи 1, используя X 2 критерий Пирсона, на уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х – время обслуживания клиентов – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
Скачать решение
Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб. По исходным данным:
Задание 13.1.
13.1.1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения.
13.1.2. Рассчитайте числовые характеристики ряда распределения предприятий по сумме прибыли: среднюю арифметическую, среднее квадратическое отклонение, дисперсию, коэффициент вариации V. Сделайте выводы.
Задание 13.2.
13.2.1. Определите границы, в которых с вероятностью 0.997 заключена сумма прибыли одного предприятия в генеральной совокупности.
13.2.2. Используя x2-критерий Пирсона, при уровне значимости α проверить гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.
Задание 13.3.
13.3.1. Определите коэффициенты выборочного уравнения регрессии.
13.3.2. Установите наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Постройте диаграмму рассеяния и линию регрессии.
13.3.3. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами X и Y, используя шкалу Чеддока.
Методические рекомендации. Задание 13.3 выполняется с помощью этого сервиса.
Скачать решение
Задача. Следующие данные представляют собой затраты времени клиентов на заключение договоров. Построить интервальный вариационный ряд представленных данных, гистограмму, найти несмещенную оценку математического ожидания, смещенную и несмещенную оценку дисперсии.
Решение:
Для построения группировка с равными интервалами воспользуемся сервисом Группировка статистических данных.
Диаграмма распределения осадков в Excel
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
Как построить диаграмму распределения в Excel
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
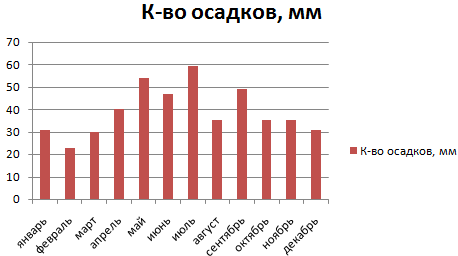
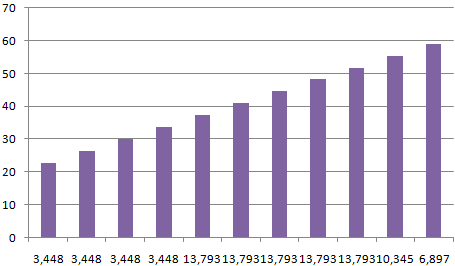
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
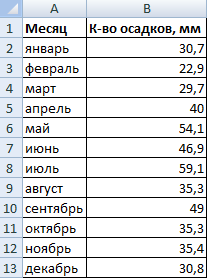
Имеются следующие данные о количестве выпавших осадков:
Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):
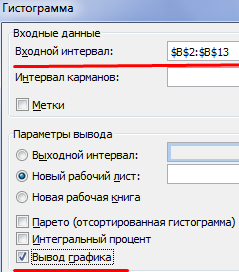
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:
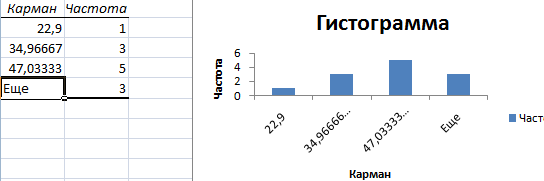
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
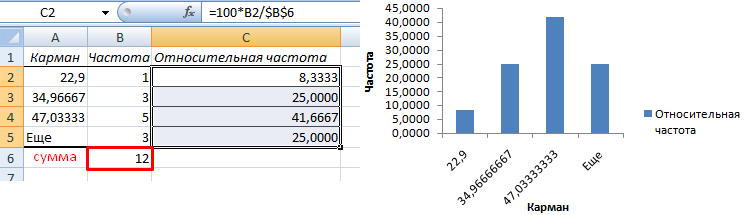
Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:
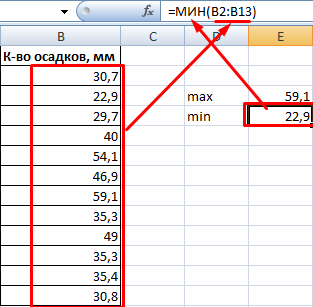
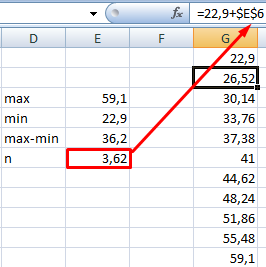
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
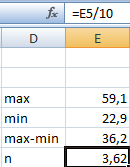
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
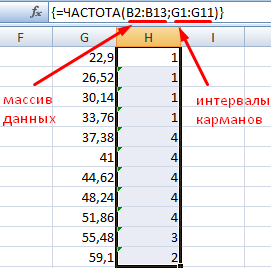
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
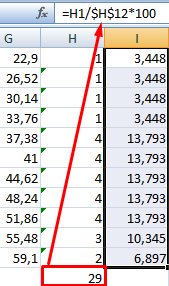
Вычислим относительные частоты (как в предыдущем способе).
Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
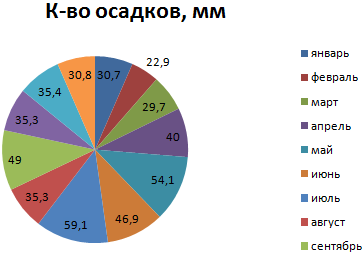
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
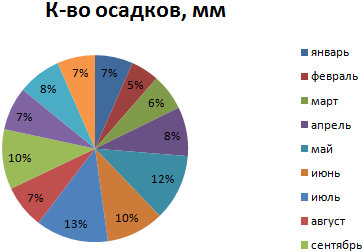
Доля «каждого месяца» в общем количестве осадков за год:
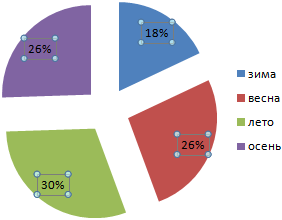
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
График нормального распределения в Excel
График нормального распределения в Excel используется для представления явления нормального распределения заданных данных, этот график создается после вычисления среднего и стандартного отклонения для данных, а затем вычисления нормального отклонения по ним, из версий Excel 2013 было легко Постройте график нормального распределения, поскольку он имеет встроенную функцию для расчета нормального распределения и стандартного отклонения, график очень похож на колоколообразную кривую.
График нормального распределения Excel (кривая колокола)
График нормального распределения — это непрерывная функция вероятности. Все мы знаем, что такое вероятность; это метод расчета возникновения явления или переменной. Распределение вероятностей — это функция, которая используется для вычисления появления переменной. Существует два типа вероятностных распределений: дискретное и непрерывное.
Основная идея того, что такое нормальное распределение, объясняется в обзоре выше. По определению, нормальное распределение означает, насколько равномерно распределяются данные. Непрерывное распределение вероятностей используется для расчета появления любого явления в реальном времени. В математике уравнение распределения вероятностей выглядит следующим образом:
Кажется таким сложным, правда? Но Excel упростил нам вычисление нормального распределения, поскольку он имеет встроенную функцию в excel нормального распределения. В ячейках любого типа следующая формула,
Для расчета нормального распределения в Excel используются три основных фактора:
График, который мы строим на основе этих данных, называется графиком нормального распределения. Это также известно как кривая колокола. Что такое колоколообразная кривая? Колоколообразная кривая — это обычное распределение для переменной, т. Е. Насколько равномерно распределяются данные. Есть некоторые. График, который мы строим, может быть линейным или точечной диаграммой со сглаженными линиями.
Как составить нормальный график распределения в Excel?
Ниже приведены примеры графиков нормального распределения в Excel (кривая Белла)
Пример графа нормального распределения # 1
Итак, взгляните на данные ниже.
Нажмите Enter, чтобы получить результат.
Нажмите Enter, чтобы получить результат.
Приведенная выше диаграмма представляет собой график нормального распределения для взятых нами случайных данных. Теперь нам нужно сначала кое-что понять, прежде чем мы перейдем к реальному примеру данных. Стандартное отклонение S означает выборку стандартного отклонения, потому что в реальном анализе данных у нас есть огромный кусок данных, и мы выбираем из него образец данных для анализа.
Пример графа нормального распределения # 2
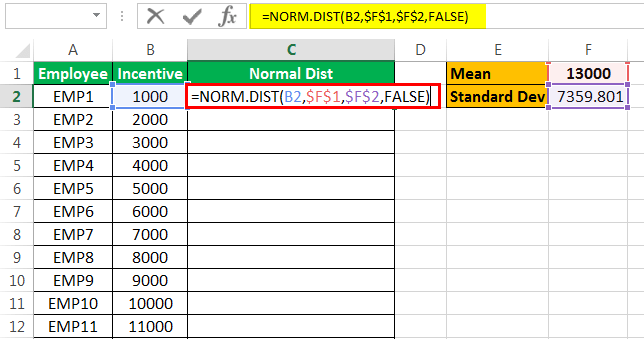
Переходим к примеру из жизни. Чем больше данных у нас есть, тем более гладкую линию мы получим для нашей колоколообразной кривой или графика нормального распределения Excel. Чтобы доказать это, я возьму пример сотрудников и их стимулы, достигнутые в текущем месяце. Возьмем пример для 25 сотрудников.
Обратите внимание на данные ниже.
Среднее значение данных составляет 13000.
Стандартное отклонение данных составляет 7359.801.
В качестве выборки данных мы взяли 25 сотрудников; мы можем видеть, что на горизонтальной оси кривая заканчивается на 25.
Приведенная выше диаграмма представляет собой график нормального распределения или кривую колокола для данных для сотрудников и стимулов, которых они достигли за текущий месяц.
Нормальное распределение Excel — это в основном процесс анализа данных, для которого требуется несколько функций, таких как среднее и стандартное отклонение данных. График полученного нормального распределения известен как график нормального распределения или колоколообразная кривая.
Как сделать график распределения в excel?
Очень давно не писал блог. Расслабился совсем. Ну ничего, исправляюсь.
Продолжаю новую рубрику блога, посвященную анализу данных с помощью всем известного Microsoft Excel.
В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: естественно, в первую очередь я скажу, что металлургии, а также в экономике, биологии, политике, социологии и… много где еще. Статья эта будет, как несложно догадаться по ее названию, про использование некоторых средств статистического анализа, а именно — гистограммам.
Ну, поехали.
Статистический анализ в Excel можно осуществлять двумя способами:
• С помощью функций
• С помощью средств надстройки «Пакет анализа». Ее, как правило, еще необходимо установить.
Чтобы установить пакет анализа в Excel, выберите вкладку «Файл» (а в Excel 2007 это круглая цветная кнопка слева сверху), далее — «Параметры», затем выберите раздел «Надстройки». Нажмите «Перейти» и поставьте галочку напротив «Пакет анализа».
А теперь — к построению гистограмм распределения по частоте и их анализу.
Речь пойдет именно о частотных гистограммах, где каждый столбец соответствует частоте появления* значения в пределах границ интервалов. Например, мы хотим посмотреть, как у нас выглядит распределение значения предела текучести стали S355J2 в прокате толщиной 20 мм за несколько месяцев. В общем, хотим посмотреть, похоже ли наше распределение на нормальное (а оно должно быть таким).
*Примечание: для металловедческих целей типа оценки размера зерна или оценки объемной доли частиц этот вид гистограмм не пойдет, т.к. там высота столбика соответствует не частоте появления частиц определенного размера, а доле объема (а в плоскости шлифа — площади), которую эти частицы занимают.
График нормального распределения выглядит следующим образом:
График функции Гаусса
Мы знаем, что реально такой график может быть получен только при бесконечно большом количестве измерений. Реально же для конечного числа измерений строят гистограмму, которая внешне похожа на график нормального распределения и при увеличении количества измерений приближается к графику нормального распределения (распределения Гаусса).
Построение гистограмм с помощью программ типа Excel является очень быстрым способом проверки стабильности работы оборудования и добросовестности коллектива: если получим «кривую» гистограмму, значит, либо прибор не исправен или мы данные неверно собрали, либо кто-то где-то преднамеренно мухлюет или же просто неверно использует оборудование.
А теперь — построение гистограмм!
Способ 1-ый. Халявный.
Способ 2-ой. Трудный, но интересный.
Будет полезен тому, кто по каким-либо причинам не смог установить Пакет анализа.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Поделиться ссылкой:
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
Как построить диаграмму распределения в Excel
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
Имеются следующие данные о количестве выпавших осадков:
Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
Вычислим относительные частоты (как в предыдущем способе).
Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
Доля «каждого месяца» в общем количестве осадков за год:
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.
Уровень сложности: продвинутый.
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:
Что такое гистограмма или график распределения частот?
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.
На какие вопросы отвечает гистограмма распределения?
Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.
«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:
Динамическая гистограмма
После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.
Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!
Как это работает?
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.
Формулы
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.
Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.
Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.
Динамический именованный диапазон
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).
Элемент управления «Полоса прокрутки»
Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).
На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.
Гистограмма
График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.
Есть вопросы?
Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.
Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Более простой вариант гистограммы можно создать, используя сводные таблицы.
Пишите в комментариях любые вопросы и предложения. Спасибо!
Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевел: Антон Андронов
Правила перепечаткиЕще больше уроков по Microsoft Excel
Оцените качество статьи. Нам важно ваше мнение: