Как построить отрезок равный данному
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
Построение отрезка, равного данному
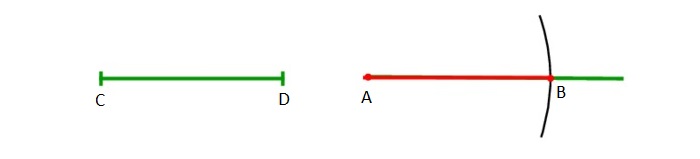
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
Имеется отрезок AB.
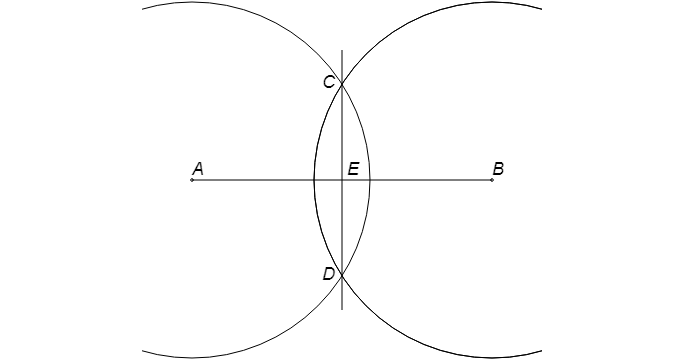
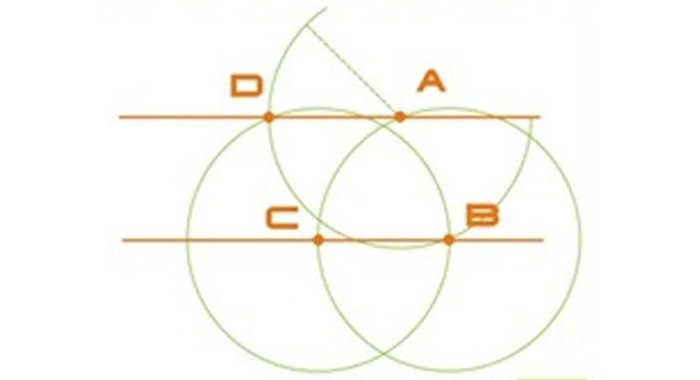
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
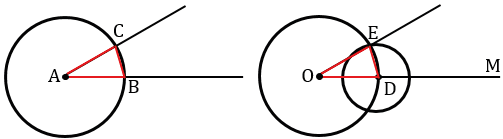
Построение угла, равного данному
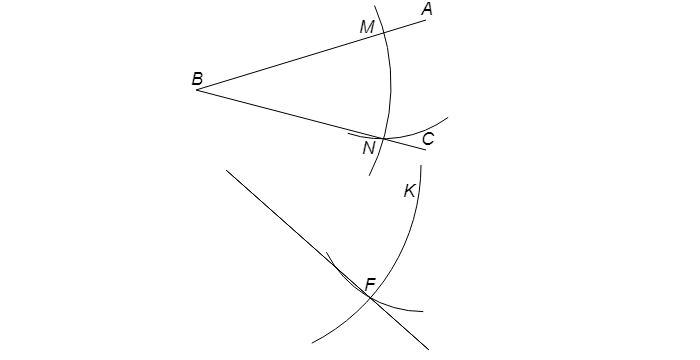
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
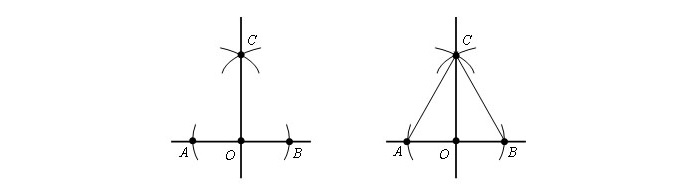
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
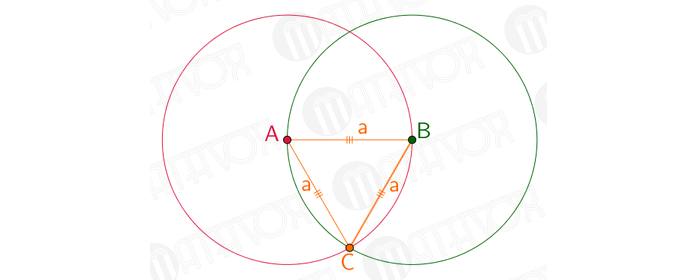
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Построение правильного четырехугольника вписанного в окружность
Вариант 1
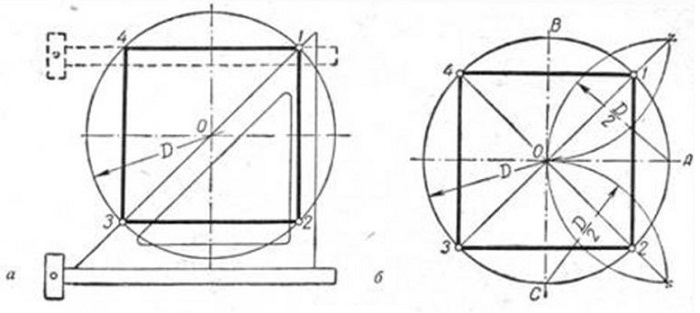
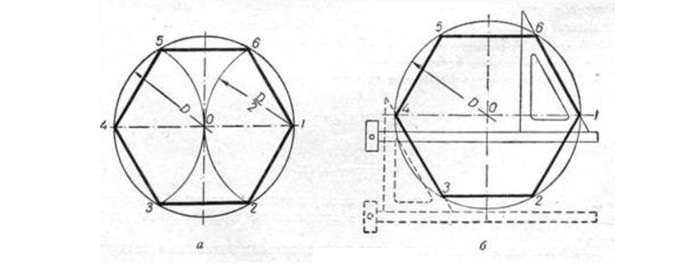
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Построение вписанного в окружность правильного пятиугольника
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.
Построение с помощью циркуля и линейки — описание, алгоритмы и задачи
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
Построение отрезка, равного данному
Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Построение угла, равного данному
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Построение правильного четырехугольника вписанного в окружность
Вариант 1
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Построение вписанного в окружность правильного пятиугольника
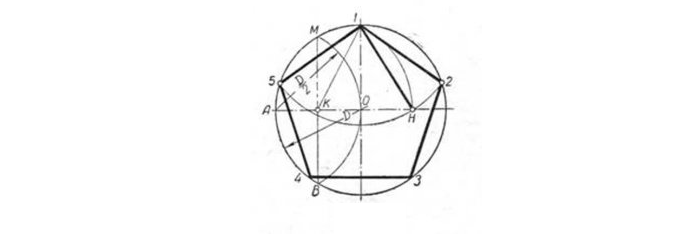
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.
3. Построить на данной прямой от данной точки в данном направлении отрезок, равный данному
Полагаем, что у нас построена прямая a, на которой отложен данный отрезок AB. Необходимо построить другой отрезок (например, CD) равный АВ. С помощью линейки постройте на листе бумаги случайную прямую b. Нанесите на ней точку C. Измерьте циркулем расстояние между крайними точками отрезка АВ. Для этого поместите одну ножку циркуля в точку A, а другую в точку B. Не изменяя раствора циркуля, переставьте иглу циркуля из точки A в точку C. Другой ножкой циркуля отметьте на прямой точку. Это и будет искомая точка D. Выделите получившийся отрезок CD более жирной линией.
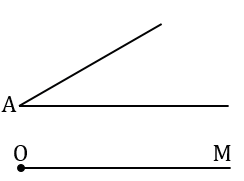
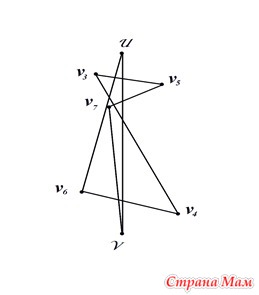
4. Построить угол с вершиной в данной точке с данной стороной угла по указанную сторону от нее и равный данному углу
Полагаем, что нам дан угол с вершиной В и дана точка А на прямой МР, выше которой нужно отложить данный угол В.
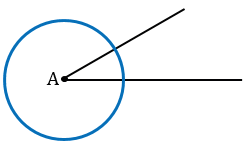
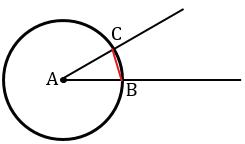
От вершины угла В отложите равные отрезки, используя один раствор циркуля. Не сдвигая ножек, опишите этим же радиусом из точки А дугу выше прямой МР до пересечения с ней – получили точку К. Не сдвигая ножек, опишите дугу тем же радиусом из точки К до пересечения с ранее построенной дугой. На пересечении двух дуг получили точку С. С помощью линейки строим прямую АС. Полученный угол САК равен данному углу В.
Построение отрезка равного данному
Построение отрезка равного данному
Просмотр содержимого документа
«Построение отрезка равного данному»
Конспект урока математики
по теме «Построение отрезка равного данному»
Тема: Построение отрезка равного данному
Перспективная цель: создание организационных и содержательных условий для углубления знаний об отрезке в ходе смены видов деятельности.
Актуальная цель: создание условий для формирования умения построения отрезка равного данному в ходе смены видов деятельности
Образовательная: учить строить отрезок равный данному в ходе выполнения практических заданий.
Развивающая: развивать логическое мышление при построении отрезков равных данным.
Воспитывающая: воспитывать сотрудничество в процессе групповой работы.
Предметные: знают алгоритм построения отрезка равного данному с помощью циркуля
Личностные: умеют адекватно оценивать собственную работу и работу в группе
Метапредметные: Регулятивные: умеют работать по алгоритму
Познавательные: умеют выдвигать гипотезы для решения проблемы
Коммуникативные: умеют планировать собственную деятельность при работе в группе
Оборудование: учебник, рабочая тетрадь
Вид урока: урок-практикум
Принципы: психологической комфортности, деятельности, непрерывности, целостности, минимакса, вариативности.
Методы: Объяснительно-иллюстративный, репродуктивный
Литература: Рудницкая. Математика. 4 кл. Учебник, рабочая тетрадь
(предметные, метапредметные, личностные)
— Добрый день! Запишите дату в тетрадях.
Ноги очень интересны
У таинственного друга:
Если первая на месте,
То другая ходит кругом!(циркуль)
Я люблю прямоту
и сама прямая.
Сделать ровную черту
Всем я помогаю.(линейка)
Он ограничен с двух сторон
И по линейке проведен.
Длину его измерить можно,
И сделать это так несложно! (Отрезок)
Как эти три слова могут быть связаны между собой
Здравствуйте! Дети слушают учителя. Подготавливаются к уроку.
С помощью циркуля и линейки можно разделить отрезок на равные части.
развитие произвольного внимания
2. Актуализация знаний.
1)У вас на партах лежат карточки с изображением отрезка. Найдите пару. Отрезок должен быть равный вашему. Измерительные инструменты использовать нельзя (2 минуты)
Назовите способы нахождения одинаковых отрезков.
Сегодня цель нашего урока научиться строить отрезки равные данным без измерений с помощью циркуля и линейки.
2) Как будем действовать? Предложите свои способы, проверяем их совместно. На партах у вас есть отрезки. (5 минут)
Ищут одинаковые отрезки
Наложение, посмотреть на свет…
Высказывают гипотезы построения отрезка равного данному
Умеют находить равные отрезки не используя измерительных материалов
Коммуникативные УУД
Развивают умение доносить свою позицию до других: оформлять свои мысли в устной и письменной речи (выражение решения учебной задачи в общепринятых формах) с учётом своих учебных речевых ситуаций; Личностные результаты
в созданных совместно с педагогом на уроке ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, как себя вести.
3. Открытие новых знаний и способов деятельности.
1)Проверим алгоритм по учебнику.
Измеряем с помощью циркуля данный отрезок
Отмеряем на луче циркулем дугу с центром в начале луча и радиусом равным отрезку
Находим точку пересечения дуги и луча.
2) Отработаем алгоритм на практике. Начертите произвольный отрезок. Постройте отрезок равный отрезку соседа по парте. Постройте каждый по два отрезка (7 минут)
Что получилось сразу?
Совместно в паре строят равные отрезки
Развитие умения добывать новые знания: извлекать информацию, представленную в форме иллюстраций
Коммуникативные УУД
Развивают умение доносить свою позицию до других: оформлять свои мысли в устной речи
перерабатывать полученную информацию: сравнивать и группировать математические факты и объекты;
делать выводы на основе обобщения умозаключений;
преобразовывать информацию из одной формы в другую;
Развивают умения составлять план решения отдельной учебной задачи;
4.Самостоятельное применение новых знаний
Сейчас поработаем в группах. Ваша задача построить точно такой же рисунок.
Вытягивают пример рисунка из отрезков, совместно строят рисунок равный данному
Развивают умения:
сверять свои действия с целью и при необходимости исправлять ошибки с помощью класса;
в диалоге с учителем и другими учащимися учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех, исходя из имеющихся критериев.
Построение угла, равного данному
Пример:
Отложить от данного луча угол, равный данному.
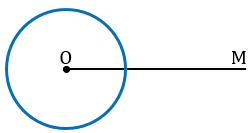
Дано: луч ОМ, 
Отложить: от луча ОМ угол, равный 
Решение:
Произвольно строим с помощью линейки 
Строим с помощью циркуля окружность произвольного радиуса с центром в вершине 
Точки пересечения окружности со сторонами 
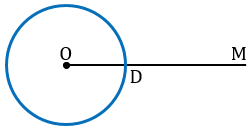
Построим с помощью циркуля окружность того же радиуса, как и окружность с центром в вершине 
Точку пересечения данной окружности с лучом ОМ обозначим D.
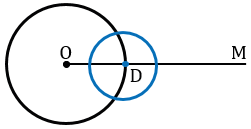
Теперь строим с помощью циркуля окружность радиуса ВС с центром в точке D.
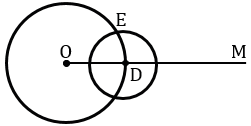
Получаем окружности с центрами в точках О и D пересекаются в двух точках, обозначим одну из этих точек Е.
С помощью линейки проведем луч ОЕ.
Рассмотрим треугольники АВС и ОDE.
Поделись с друзьями в социальных сетях: