Как построить касательную к параболе

Парабола

Парабола, её форма, фокус и директриса.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^<2>=2px\label
$$
при условии \(p > 0\).

Из уравнения \eqref вытекает, что для всех точек параболы \(x \geq 0\). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции \(y=ax^<2>\). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством \(2p=a^<-1>\).

Фокусом параболы называется точка \(F\) с координатами \((p/2, 0)\) в канонической системе координат.

Директрисой параболы называется прямая с уравнением \(x=-p/2\) в канонической системе координат (\(PQ\) на рис. 8.11).

Рис. 8.11. Парабола.

Свойства параболы.

Расстояние от точки \(M(x, y)\), лежащей на параболе, до фокуса равно
$$
r=x+\frac

<2>.\label
$$

Вычислим квадрат расстояния от точки \(M(x, y)\) до фокуса по координатам этих точек: \(r^<2>=(x-p/2)^<2>+y^<2>\) и подставим сюда \(y^<2>\) из канонического уравнения параболы. Мы получаем
$$
r^<2>=\left(x-\frac

<2>\right)^<2>+2px=\left(x+\frac

<2>\right)^<2>.\nonumber
$$
Отсюда в силу \(x \geq 0\) следует равенство \eqref.

Заметим, что расстояние от точки \(M\) до директрисы также равно
$$
d=x+\frac

<2>.\nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Для того чтобы точка \(M\) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.

Докажем достаточность. Пусть точка \(M(x, y)\) одинаково удалена от фокуса и от директрисы параболы:
$$
\sqrt<\left(x-\frac

<2>\right)^<2>+y^<2>>=x+\frac

<2>.\nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы \eqref. Это заканчивает доказательство.

Параболе приписывается эксцентриситет \(\varepsilon=1\). В силу этого соглашения формула
$$
\frac=\varepsilon\nonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке \(M_<0>(x_<0>, y_<0>)\), лежащей на ней. Пусть \(y_ <0>\neq 0\). Через точку \(M_<0>\) проходит график функции \(y=f(x)\), целиком лежащий на параболе. (Это \(y=\sqrt<2px>\) или же \(y=-\sqrt<2px>\), смотря по знаку \(y_<0>\).) Для функции \(f(x)\) выполнено тождество \((f(x))^<2>=2px\), дифференцируя которое имеем \(2f(x)f'(x)=2p\). Подставляя \(x=x_<0>\) и \(f(x_<0>)=y_<0>\), находим \(f'(x_<0>)=p/y_<0>\) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_<0>=\frac

>(x-x_<0>).\nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что \(y_<0>^<2>=2px_<0>\). Теперь уравнение касательной принимает окончательный вид
$$
yy_<0>=p(x+x_<0>).\label
$$

Заметим, что для вершины параболы, которую мы исключили, положив \(y_ <0>\neq 0\), уравнение \eqref превращается в уравнение \(x=0\), то есть в уравнение касательной в вершине. Поэтому уравнение \eqref справедливо для любой точки на параболе.

Касательная к параболе в точке \(M_<0>\) есть биссектриса угла, смежного с углом между отрезком, который соединяет \(M_<0>\) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Рассмотрим касательную в точке \(M_<0>(x_<0>, y_<0>)\). Из уравнения \eqref получаем ее направляющий вектор \(\boldsymbol(y_<0>, p)\). Значит, \((\boldsymbol, \boldsymbol_<1>)=y_<0>\) и \(\cos \varphi_<1>=y_<0>/\boldsymbol\). Вектор \(\overrightarrow>\) имеет компоненты \(x_<0>=p/2\) и \(y_<0>\), а потому
$$
(\overrightarrow>, \boldsymbol)=x_<0>y_<0>-\frac

<2>y_<0>+py_<0>=y_<0>(x_<0>+\frac

<2>).\nonumber
$$
Но \(|\overrightarrow>|=x_<0>+p/2\). Следовательно, \(\cos \varphi_<2>=y_<0>/|\boldsymbol|\). Утверждение доказано.

Заметим, что \(|FN|=|FM_<0>|\) (см. рис. 8.12).

Источник

Общая касательная к графикам функций. На примере 2х парабол

На примере двух парабол покажем, как составить уравнение общей касательной к графикам функций. Заметим, что общих касательных может быть несколько.

Для решения данной задачи потребуются знания о производной на уровне школьного курса.

В рамках подготовки к профильному ЕГЭ при изучении производной я предлагаю своим ученикам решать, в том числе, и подобные задачи, помимо стандартных 7 и 12 заданий.

Это необходимо для того, чтобы школьники учились применять свои знания при решении задач, а не просто решать стандартные задания по шаблону.

Составим уравнение общих касательных к графикам квадратичных функций (параболам):

Касательная представляет собой прямую. Запишем уравнение касательной в виде уравнения прямой с угловым коэффициентом:
y = kx + b, k – угловой коэффициент.
Обозначим точку, в которой она касается первой параболы, как A (a1, a2), второй параболы – B (b1, b2).

Рассмотрим функцию

1. Вычислим ее производную: y’ = 2(x – 1).

Таким образом, мы выразили координаты точки A через угловой коэффициент касательной:
A (k/2 + 1, k^2/4 + 1).

3. Угловой коэффициент прямой, проходящей через точки A (a1, a2) и B (b1, b2), равен (a2 – b2) / (a1 – b1). Значит
k = (a2 – b2) / (a1 – b1).

Подставим в это уравнение координаты точек A и B и получим уравнение относительно k:

Находим корни: k = 0 и k = 4.

5. Составляем уравнение касательной (прямой) по двум точкам. (Данная тема разобрана в предыдущем посте)
(x – a1) / (b1 – a1) = (y – a2) / (b2 – a2)
(x – 3) / (1 – 3) = (y – 5) / (-3 – 5)
(x – 3) / (–2) = (y – 5) / (-8) – каноническое уравнение прямой
Выражаем y:
y = 4x – 7 – уравнение прямой с угловым коэффициентом.

Аналогично находим уравнение еще одной касательной (при k = 0):
y = 1.

✔ Для того, чтобы задать вопрос или записаться на консультацию, пишите в whatsapp 8 968 814 30 80.

Источник

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

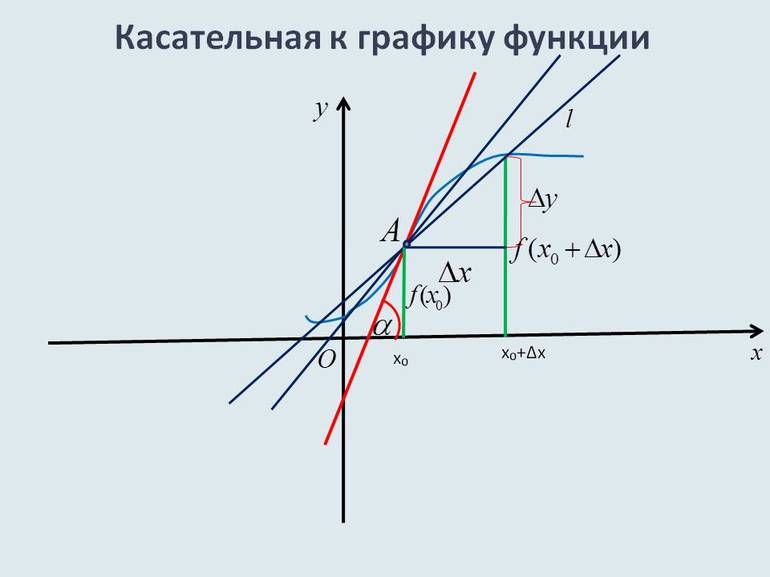
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Решение

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

Для наглядности изобразим графически.

Решение

Необходимо продифференцировать функцию. Имеем, что

Вычисляем соответствующие значения функции

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

Другое уравнение имеет два действительных корня, тогда

Перейдем к нахождению значений функции. Получаем, что

Возможно существование бесконечного количества касательных для заданных функций.

Решение

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

Ответ: необходимы уравнения запишутся как

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Данное равенство может быть записано как объединение двух функций:

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Касательная к эллипсу

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

Решение

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

Графически касательные обозначаются так:

Касательная к гиперболе

Гипербола может быть представлена в виде двух объединенных функций вида

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

Ответ: уравнение касательной можно представить как

Наглядно изображается так:

Касательная к параболе

Графически изобразим как:

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

Отсюда определим значение х для точек касания.

Первая функция запишется как

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

Ответ: уравнение касательной принимает вид

Источник

Однако следует разобраться в основных терминах и соотношениях.

Специалисты рекомендуют пользоваться специальным алгоритмом, позволяющим правильно находить точку касания прямой с какой-либо фигурой.

Общие сведения

Касательной называется прямая, имеющая с фигурой или графиком заданной функции одну общую точку. Однако иногда она проходит через 2 точки. В этом случае ее называют секущей. Прямая задается следующим уравнением: y = kx + b. Значение «k» — это угловой коэффициент.

Для решения задач следует разобрать основные понятия, определения, формулы и свойства касательной.

Кроме того, очень важно понять ее геометрический смысл, поскольку без него будет сложно разобраться в более сложных дисциплинах с физико-математическим уклоном.

Определения и понятия

У касательной есть определенный параметр — угол наклона (а).

Его необходимо отсчитывать от оси абсцисс (только положительное направление) к прямой, заданной графиком y = kx + b.

От него зависит ее расположение.

Коэффициент «к» равен значению тангенса угла наклона, т. е. tg(a).

Математики сделали некоторые выводы, которые основываются на значении углового коэффициента:

В первом, втором и третьем случаях коэффициент является положительным, а в последнем — отрицательным. Эти факты следует учитывать при решении задач. Касательная прямая может являться и секущей, т. е. соприкасаться с графиком функции сразу в двух и более точках. Следует отметить, что при параллельности прямой оси ОХ (y = b), она может пересекать функцию бесконечное число раз.

Геометрический смысл

Рисунок 1. Геометрический смысл.

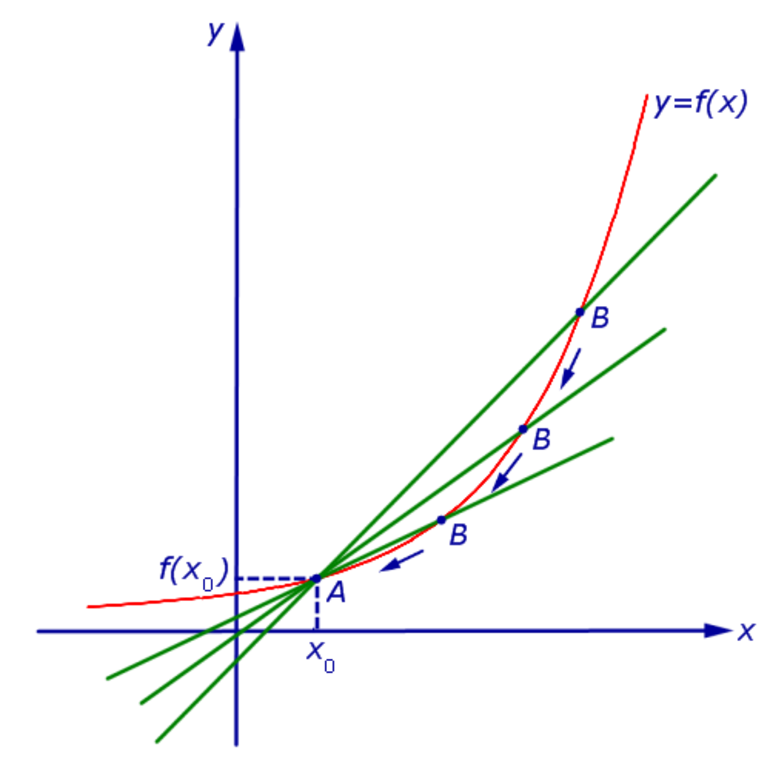
Соотношение, которое было получено выше, называется производной. Если к графику в точке проведена секущая или касательная, то тангенс угла будет равен самой производной заданной функции в точке с координатой х0.

Из этого определения можно сделать вывод о существовании производной. Если значение последней равно 0, то, следовательно, не существует общих точек с заданной фигурой.

Касательные к фигурам и графикам

При решении задач следует обратить внимание на частные случаи. Нужно произвести расчеты уравнения прямой или найти точки соприкосновения с окружностью, эллипсом, гиперболой или параболой. Очень распространенная задача встречается также в механике о ременной передаче.

Частные случаи позволят найти оптимальное решение и метод расчета, поскольку экономия времени является важным элементом при научных исследованиях, написании контрольных работ и сдаче экзаменов. Важный этап — идентификация типа задачи. Касательная к вышеперечисленным фигурам — основной тип заданий, но существуют и более сложные функции.

Например, сложно составить уравнение прямой, которая имеет точки касания с какой-либо сложной функцией.

В некоторых случаях необходимо перед выполнением расчетов ее упростить, т. е. привести подобные слагаемые, раскрыть скобки или воспользоваться другими приемами для упрощения выражения.

Одна и несколько окружностей

Формула окружности с центром в точке О (xc;yc) и радиусом R имеет следующий вид: sqr(х-хc) + sqr(y-yc) = R^2.

Для решения следует выразить значение у, но при этом нужно рассматривать 2 случая:

В случае для двух окружностей всего можно провести до 4 касательных (2 внешних и 2 внутренних). Это зависит от случая расположения фигур. Точкой пересечения внешних считается внешняя гомотетия (подобие), а внутренних — в центре внутреннего подобия. Внешними называются прямые, которые касаются внешних точек круга. Если касательные являются внутренними, то они пересекают линию, соединяющую центры окружностей.

Следует отметить, что внешний и внутренний центры гомотетии лежат на некоторой прямой. Она проходит через центры заданных окружностей. Это был рассмотрен случай, когда одна окружность меньше другой.

Однако при равенстве их диаметров появляются некоторые свойства: внешние касательные параллельны и внешнего центра гомотетии не существует.

Эллипс, гипербола и парабола

Пусть задан эллипс с полуосями a и b.

В зависимости от его значения находятся корни:

Источник

Уравнение касательной к графику функции

Статья опубликована при поддержке Гостиничного комплекса «ИТАКА+». Останавливаясь в городе судостроителей Северодвинске, вы не столкнетесь с проблемой поиска временного жилья. Тут, на сайте гостиничного комплекса «ИТАКА+» http://itakaplus.ru, вы сможете легко и быстро снять квартиру в городе, на любой срок, с посуточной оплатой.

На современном этапе развития образования в качестве одной из основных его задач выступает формирование творчески мыслящей личности. Способность же к творчеству у учащихся может быть развита лишь при условии систематического привлечения их к основам исследовательской деятельности. Фундаментом для применения учащимися своих творческих сил, способностей и дарований являются сформированные полноценные знания и умения. В связи с этим проблема формирования системы базовых знаний и умений по каждой теме школьного курса математики имеет немаловажное значение. При этом полноценные умения должны являться дидактической целью не отдельных задач, а тщательно продуманной их системы. В самом широком смысле под системой понимается совокупность взаимосвязанных взаимодействующих элементов, обладающая целостностью и устойчивой структурой.

Рассмотрим методику обучения учащихся составлению уравнения касательной к графику функции. По существу, все задачи на отыскание уравнения касательной сводятся к необходимости отбора из множества (пучка, семейства) прямых тех из них, которые удовлетворяют определенному требованию – являются касательными к графику некоторой функции. При этом множество прямых, из которого осуществляется отбор, может быть задано двумя способами:

а) точкой, лежащей на плоскости xOy (центральный пучок прямых);
б) угловым коэффициентом (параллельный пучок прямых).

В связи с этим при изучении темы «Касательная к графику функции» с целью вычленения элементов системы нами были выделены два типа задач:

1) задачи на касательную, заданную точкой, через которую она проходит;
2) задачи на касательную, заданную ее угловым коэффициентом.

Обучение решению задач на касательную осуществлялось при помощи алгоритма, предложенного А.Г. Мордковичем [2]. Его принципиальное отличие от уже известных заключается в том, что абсцисса точки касания обозначается буквой a (вместо x0), в связи с чем уравнение касательной приобретает вид

(сравните с y = f(x₀) + f ‘(x₀)(x – x₀)). Этот методический прием, на наш взгляд, позволяет учащимся быстрее и легче осознать, где в общем уравнении касательной записаны координаты текущей точки, а где – точки касания.

Алгоритм составления уравнения касательной к графику функции y = f(x)

1. Обозначить буквой a абсциссу точки касания.
2. Найти f(a).
3. Найти f ‘(x) и f ‘(a).
4. Подставить найденные числа a, f(a), f ‘(a) в общее уравнение касательной y = f(a) = f ‘(a)(x – a).

Этот алгоритм может быть составлен на основе самостоятельного выделения учащимися операций и последовательности их выполнения.

Практика показала, что последовательное решение каждой из ключевых задач при помощи алгоритма позволяет формировать умения написания уравнения касательной к графику функции поэтапно, а шаги алгоритма служат опорными пунктами действий. Данный подход соответствует теории поэтапного формирования умственных действий, разработанной П.Я. Гальпериным и Н.Ф. Талызиной [3].

Задача 1. Составьте уравнение касательной к графику функции в точке M(3; – 2).

Решение. Точка M(3; – 2) является точкой касания, так как

1. a = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f ‘(x) = x 2 – 4, f ‘(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.

Задача 2. Напишите уравнения всех касательных к графику функции y = – x 2 – 4x + 2, проходящих через точку M(– 3; 6).

Решение. Точка M(– 3; 6) не является точкой касания, так как f(– 3) ­ 6 (рис. 2).

1. a – абсцисса точки касания.
2. f(a) = – a 2 – 4a + 2.
3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.

Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a₁ = – 4, a₂ = – 2.

Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.

Если a = – 2, то уравнение касательной имеет вид y = 6.

Задача 3. Напишите уравнения всех касательных к графику функции y = x 3 – 3x 2 + 3, параллельных прямой y = 9x + 1.

1. a – абсцисса точки касания.
2. f(a) = a 3 – 3a 2 + 3.
3. f ‘(x) = 3x 2 – 6x, f ‘(a) = 3a 2 – 6a.

Но, с другой стороны, f ‘(a) = 9 (условие параллельности). Значит, надо решить уравнение 3a 2 – 6a = 9. Его корни a = – 1, a = 3 (рис. 3).

y = 9x + 8 – уравнение касательной;

y = 9x – 24 – уравнение касательной.

Задача 4. Напишите уравнение касательной к графику функции y = 0,5x 2 – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. 4).

Решение. Из условия f ‘(a) = tg 45° найдем a: a – 3 = 1 ^ a = 4.

1. a = 4 – абсцисса точки касания.
2. f(4) = 8 – 12 + 1 = – 3.
3. f ‘(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – уравнение касательной.

Несложно показать, что решение любой другой задачи сводится к решению одной или нескольких ключевых задач. Рассмотрим в качестве примера следующие две задачи.

1. Напишите уравнения касательных к параболе y = 2x 2 – 5x – 2, если касательные пересекаются под прямым углом и одна из них касается параболы в точке с абсциссой 3 (рис. 5).

Решение. Поскольку дана абсцисса точки касания, то первая часть решения сводится к ключевой задаче 1.

1. a = 3 – абсцисса точки касания одной из сторон прямого угла.
2. f(3) = 1.
3. f ‘(x) = 4x – 5, f ‘(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой касательной.

Пусть a – угол наклона первой касательной. Так как касательные перпендикулярны, то – угол наклона второй касательной. Из уравнения y = 7x – 20 первой касательной имеем tg a = 7. Найдем

Это значит, что угловой коэффициент второй касательной равен .

Дальнейшее решение сводится к ключевой задаче 3.

Пусть B(c; f(c)) есть точка касания второй прямой, тогда

1. – абсцисса второй точки касания.
2.
3.
4.
– уравнение второй касательной.

Примечание. Угловой коэффициент касательной может быть найден проще, если учащимся известно соотношение коэффициентов перпендикулярных прямых k₁•k₂ = – 1.

2. Напишите уравнения всех общих касательных к графикам функций

Решение. Задача сводится к отысканию абсцисс точек касания общих касательных, то есть к решению ключевой задачи 1 в общем виде, составлению системы уравнений и последующему ее решению (рис. 6).

1. Пусть c – абсцисса точки касания, лежащей на графике функции
2.
3. f ‘(c) = c.
4.

Так как касательные общие, то

Итак, y = x + 1 и y = – 3x – 3 – общие касательные.

Основная цель рассмотренных задач – подготовить учащихся к самостоятельному распознаванию типа ключевой задачи при решении более сложных задач, требующих определенных исследовательских умений (умения анализировать, сравнивать, обобщать, выдвигать гипотезу и т. д.). К числу таких задач можно отнести любую задачу, в которую ключевая задача входит как составляющая. Рассмотрим в качестве примера задачу (обратную задаче 1) на нахождение функции по семейству ее касательных.

3. При каких b и c прямые y = x и y = – 2x являются касательными к графику функции y = x 2 + bx + c?

Составим и решим систему уравнений

Ответ:

Задачи для самостоятельного решения

1. Напишите уравнения касательных, проведенных к графику функции y = 2x 2 – 4x + 3 в точках пересечения графика с прямой y = x + 3.

Ответ: y = – 4x + 3, y = 6x – 9,5.

2. При каких значениях a касательная, проведенная к графику функции y = x 2 – ax в точке графика с абсциссой x₀ = 1, проходит через точку M(2; 3)?

3. При каких значениях p прямая y = px – 5 касается кривой y = 3x 2 – 4x – 2?

4. Найдите все общие точки графика функции y = 3x – x 3 и касательной, проведенной к этому графику через точку P(0; 16).

Ответ: A(2; – 2), B(– 4; 52).

5. Найдите кратчайшее расстояние между параболой y = x 2 + 6x + 10 и прямой

Ответ:

6. На кривой y = x 2 – x + 1 найдите точку, в которой касательная к графику параллельна прямой y – 3x + 1 = 0.

7. Напишите уравнение касательной к графику функции y = x 2 + 2x – | 4x |, которая касается его в двух точках. Сделайте чертеж.

8. Докажите, что прямая y = 2x – 1 не пересекает кривую y = x 4 + 3x 2 + 2x. Найдите расстояние между их ближайшими точками.

Ответ:

9. На параболе y = x 2 взяты две точки с абсциссами x₁ = 1, x₂ = 3. Через эти точки проведена секущая. В какой точке параболы касательная к ней будет параллельна проведенной секущей? Напишите уравнения секущей и касательной.

Ответ: y = 4x – 3 – уравнение секущей; y = 4x – 4 – уравнение касательной.

10. Найдите угол q между касательными к графику функции y = x 3 – 4x 2 + 3x + 1, проведенными в точках с абсциссами 0 и 1.

11. В каких точках касательная к графику функции образует с осью Ox угол в 135°?

12. В точке A(1; 8) к кривой проведена касательная. Найдите длину отрезка касательной, заключенного между осями координат.

Ответ:

13. Напишите уравнение всех общих касательных к графикам функций y = x 2 – x + 1 и y = 2x 2 – x + 0,5.

Ответ: y = – 3x и y = x.

14. Найдите расстояние между касательными к графику функции параллельными оси абсцисс.

Ответ:

15. Определите, под какими углами парабола y = x 2 + 2x – 8 пересекает ось абсцисс.

Ответ: q ₁ = arctg 6, q ₂ = arctg (– 6).

16. На графике функции найдите все точки, касательная в каждой из которых к этому графику пересекает положительные полуоси координат, отсекая от них равные отрезки.

17. Прямая y = 2x + 7 и парабола y = x 2 – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N.

18. При каких значениях b прямая y = 9x + b является касательной к графику функции y = x 3 – 3x + 15?

19. При каких значениях k прямая y = kx – 10 имеет только одну общую точку с графиком функции y = 2x 2 + 3x – 2? Для найденных значений k определите координаты точки.

20. При каких значениях b касательная, проведенная к графику функции y = bx 3 – 2x 2 – 4 в точке с абсциссой x₀ = 2, проходит через точку M(1; 8)?

21. Парабола с вершиной на оси Ox касается прямой, проходящей через точки A(1; 2) и B(2; 4), в точке B. Найдите уравнение параболы.

Ответ:

22. При каком значении коэффициента k парабола y = x 2 + kx + 1 касается оси Ox?

23. Найдите углы между прямой y = x + 2 и кривой y = 2x 2 + 4x – 3.

Ответ:

24. Определите, под какими углами пересекаются графики функций y = 2x 2 + 3x – 3 и y = x 2 + 2x + 3.

Ответ:

25. При каком значении k угол между кривыми y = x 2 + 2x + k и y = x 2 + 4x + 4 будет равен 45°?

26. Найдите все значения x0, при каждом из которых касательные к графикам функции y = 5cos 3x + 2 и y = 3cos 5x в точках в абсциссой x₀ параллельны.

Ответ:

27. Под каким углом видна окружность x 2 + y 2 = 16 из точки (8; 0)?

Ответ:

28. Найдите геометрическое место точек, из которых парабола y = x 2 видна под прямым углом?

Ответ: прямая

29. Найдите расстояние между касательными к графику функции образующими с положительным направлением оси Ox угол 45°.

Ответ:

30. Найдите геометрическое место вершин всех парабол вида y = x 2 + ax + b, касающихся прямой y = 4x – 1.

Ответ: прямая y = 4x + 3.

Литература

1. Звавич Л.И., Шляпочник Л.Я., Чинкина М.В. Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы. – М., Дрофа, 1999.
2. Мордкович А. Семинар четвертый для молодых учителей. Тема «Приложения производной». – М., «Математика», № 21/94.
3. Формирование знаний и умений на основе теории поэтапного усвоения умственных действий. / Под ред. П.Я. Гальперина, Н.Ф. Талызиной. – М., МГУ, 1968.

Источник