векторное поле в математике

Скалярное поле. Векторное поле. Основные понятия и задачи

Понятие поля в математике

В задачах физики чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные.

Скалярное поле: определение, поверхности уровня и линии уровня

Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику тепла, температура выше, чем в точках, расположенных дальше от источника тепла. Можно привести и такие примеры, как поле освещённости, поле плотности массы и тому подобные.

Определение. Поверхностью уровня скалярного поля называется множество всех тех точек пространства, в которых скалярное поле постоянно.

Уравнение поверхности уровня скалярного поля u(x,y,z) :

При постоянном изменении значения C поверхности уровня заполняют всю область пространства. Если поверхности уровня размещены плотно, скалярное поле изменяется быстро. Если же поверхности уровня расположены редко, скалярное поле изменяется медленно.

Определение. Линией уровня скалярного поля называется множество всех тех точек на плоскости, в которых скалярное поле постоянно.

Уравнение линии уровня скалярного поля u(x,y) :

Пример 1. Определить поверхности уровня скалярного поля и их вид.

Решение. Уравнением поверхностей уровня данного скалярного поля является

.

Пример 2. Определить линии уровня скалярного поля и их вид.

Решение. Уравнением линий уровня данного скалярного поля является

.

Из этого уравнения выразим «игрек»:

.

Векторное поле: определение, векторные линии

Понятие векторного поля во многом аналогично понятию скалярного поля.

Определение векторного поля. Если в некоторой области пространства каждой точке M по определённому закону ставится в соответствие вектор , то векторная функция называется полем вектора или векторным полем.

Таким образом, векторным полем является векторная функция точки пространства

Примерами векторного поля являются поля скорости и ускорения в текущей жидкости или газе, поле силы гравитации, поле интенсивности электростатического поля и тому подобные. Вообще, примером векторного поля может служить поле сил любой природы.

Мы будем рассматривать только стационарные векторные поля, то есть поля, не зависящие от времени.

.

Определение. Векторной линией называется линия, направление которой в каждой точке касательной совпадает с направлением вектора поля в этой точке (рисунок ниже).

Уравнения векторных линий можно найти, решив систему дифференциальных уравнений

.

Пример 3. Найти линии вектора поля .

Решение. Так как , , , получаем систему дифференциальных уравнений

.

Из первого равенства получаем

где . Из последнего равенства следует . Таким образом, получаем

И получаем уравнения векторных линий данного векторного поля:

Источник

Векторное поле

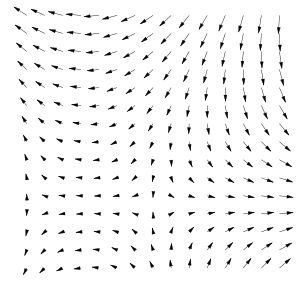
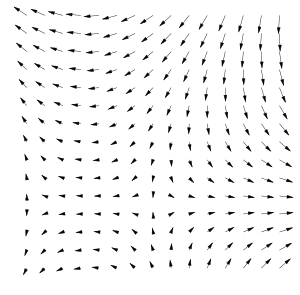
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени изменяется от точки к точке и может быть описан векторным полем.

Содержание

Определение и вариации

Евклидово пространство

Векторное поле на евклидовом (или псевдоевклидовом) пространстве [1] определяется как вектор-функция точки пространства, отображающая это пространство в (на) себя [2] :

Многообразие

В более общем случае, когда исходное пространство является многообразием, векторное поле определяется как сечение касательного расслоения к данному многообразию, то есть отображение, которое каждой точке ставит в соответствие вектор из касательного пространства в .

В физике

В физике термин векторное поле, кроме общего значения, описанного выше, имеет специальное значение, в основном в отношении фундаментальных полей (см. ниже). Смысл этого употребления сводится к тому, что фундаментальные физические поля классифицируются по природе их потенциала, и один из таких типов — векторные поля (как электромагнитное или глюонное поля).

Обозначения

Обозначается векторное поле обычно просто в соответствии с соглашениями, принятыми для векторов

где — символическое обозначение точки пространства,

где — радиус-вектор, характеризующий точку пространства.

Достаточно обычно задание векторного поля как функции координат в пространстве, на котором поле задано, например:

или (для поля, зависящего от времени):

История термина

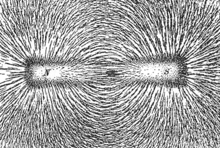
Термин поле (вместе с понятием силовых линий поля) (англ. field, lines of force ) ввёл в физику Майкл Фарадей около 1830 г. при исследовании электромагнитных явлений.

Основы аналитической теории силовых полей разработали Максвелл, Гиббс и Хевисайд во второй половине XIX века.

Частные случаи векторных полей

Векторные поля на прямой

Любую вещественнозначную функцию вещественного переменного можно интерпретировать как одномерное векторное поле.

Векторные поля на плоскости

Если — радиус-вектор, который в заданной системе координат имеет вид , то векторное поле описывается вектор-функцией вида:

Векторные поля в трёхмерном пространстве

Если — радиус-вектор, который в заданной системе координат имеет вид , то векторное поле описывается вектор-функцией вида:

В трёхмерном пространстве имеют смысл следующие характеристики векторного поля

Криволинейный интеграл

где точка означает скалярное произведение, — векторный элемент криволинейного пути, вдоль которого происходит интегрирование, — проекция на (положительную) касательную к криволинейному пути, — скалярный элемент пути (элемент длины), C — конкретная кривая — путь интегрирования (обычно полагаемая достаточно гладкой). Пожалуй, простейшим физическим прообразом такого интеграла является работа силы , действующей на точку при перемещении точки по заданному пути.

Циркуляция

— интеграл по замкнутому контуру:

где подынтегральное выражение совпадает с описанным чуть выше, а отличие состоит в пути интегрирования C, который в данном случае по определению замкнут, что обозначается кружком на знаке интеграла.

Поток векторного поля

через поверхность S определяется как интеграл по S:

,

где — проекция вектора поля на нормаль к поверхности, — «векторный элемент поверхности», определяемый, как вектор единичной нормали, умноженный на . Простейшим примером этой конструкции является объём жидкости, проходящий через поверхность S, при её течении со скоростью F.

Производная

Аналогом производной для векторного поля выступает тензор частных производных (якобиан), который в декартовых координатах имеет вид:

Дивергенция

— след такого тензора производных. Она не зависит от системы координат (является инвариантом преобразований координат, скаляром), а в прямоугольных декартовых координатах вычисляется по формуле:

Это же выражение можно записать с использованием символического оператора набла

Теорема Остроградского-Гаусса позволяет вычислить поток векторного поля с помощью объёмного интеграла от дивергенции поля.

Ротор

— векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами:

,

где i, j и k — единичные орты для осей x, y и z соответственно.

Для удобства запоминания можно условно представлять ротор как векторное произведение:

Градиент

— важнейшая и простейшая операция, позволяющая получить векторное поле из скалярного поля. Полученное применением такой операции к скалярному полю f векторное поле называется градиентом f:

или, записывая с помощью наблы:

Векторное поле, дивергенция которого всюду равна нулю, называется соленоидальным; оно может быть представлено как ротор некоторого другого векторного поля.

Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым); оно может быть представлено как градиент некоторого скалярного поля (потенциала).

Имеет место теорема Гельмгольца: если всюду в области D у векторного поля определены дивергенция и ротор, то это поле может быть представлено в виде суммы потенциального и соленоидального поля.

Векторное поле, у которого и дивергенция, и ротор всюду равны нулю, называется гармоническим; его потенциал представляет собой гармоническую функцию.

Интегральные кривые (силовые линии)

Для силовых полей силовые линии наглядно показывают направление воздействия полевых сил.

Если в достаточно малой области пространства поле нигде не обращается в нуль, то через каждую точку этой области проходит одна и только одна силовая линия. Точки, где вектор поля нулевой — особые, в них направление поля не определено, и поведение силовых линий в окрестности этих точек может быть различным: возможно, через особую точку проходит бесконечно много силовых линий, но возможно, что не проходит ни одна.

Векторное поле называется полным, если его интегральные кривые определены на всём многообразии.

Векторные поля в n-мерном пространстве

Все перечисленные для векторных полей в трёхмерном пространстве конструкции и свойства непосредственно обобщаются на любую конечную размерность пространства n.

При этом большинство таких обобщений вполне тривиальны, за исключением определения ротора, для корректного построения которого в произвольном n-мерном случае, в отличие от трёхмерного, приходится воспользоваться внешним, а не векторным (которое определено лишь для трёхмерного случая) произведением. При n=2 соответствующая операция принимает вид псевдоскалярного произведения.

Кроме того, в случае произвольного n нужна определенная аккуратность c определением потока. Основные определения оказываются полностью аналогичными для потока через гиперповерхность размерности (n — 1).

Физические примеры

В физике типичными примероми векторного поля являются силовые поля (силовое поле — поле некоторой силы (зависящей от положения в пространстве тела, на которое эта сила действует) или тесно связанной с силой напряжённости поля).

Исторически гидродинамика оказала огромное влияние на формирование основных конструкций векторного анализа и самой его терминологии. Так, гидродинамическое происхождение имеют такие понятия, как

а также, в той или иной мере, и многие другие (практически каждое из них имеет если не гидродинамическое происхождение, то гидродинамическую интерпретацию).

Особенности употребления термина в физике

В целом в физике термин векторное поле имеет то же значение, что и в математике, описанное выше. В этом смысле, векторным полем можно назвать любую векторнозначную физическую величину, являющуюся функцией точки пространства, зачастую зависящую также и от времени.

Однако существует и специфический случай применения этого термина, встречающийся главным образом в классификации фундаментальных физических полей. В этом случае слова «векторное поле» подразумевают, что векторным полем (4-векторное или более высокой размерности, если мы имеем дело с абстрактными многомерными теоретическими моделями) является наиболее фундаментальная величина — потенциал, а не её производные (напряженность поля и т. п.). Так, например, к векторным полям относят электромагнитное поле, потенциал которого является 4-векторным полем, в то время как его напряженность с современной точки зрения есть тензор. Гравитационное поле называют в этом смысле тензорным, поскольку его потенциал есть тензорное поле.

Практическим синонимом слова «векторное поле» в этом смысле является в современной физике термин векторная частица (также, разводя эти близкие понятия, о векторной частице говорят как о возбуждении векторного поля, или, выражаясь несколько более традиционно — векторная частица есть квант векторного поля). Ещё один практический синоним — частица спина 1 или поле спина 1.

Из фундаментальных полей к векторным (в указанном смысле) относятся электромагнитное (фотонное), глюонное (поле сильных взаимодействий), а также поле массивных векторных бозонов — переносчиков слабого взаимодействия. Гравитационное же поле, в отличие от перечисленных, является полем тензорным.

С рассмотренной классификацией (классификацией по спину фундаментального бозонного поля) непосредственно связаны некоторые свойства соответствующего поля, например, притягиваются или отталкиваются при взаимодействии посредством этого поля частицы одинакового заряда (относящегося к данному типу взаимодействия), одинаков или противоположен такой заряд у частиц и античастиц. Частицы, взаимодействующие посредством векторного поля отталкиваются при одинаковом заряде, а притягиваются при противоположном, а пара частица — античастица имеет противоположный друг другу заряд (как, в частности, в случае электромагнитного поля) — в противоположность свойствам гравитационного поля и гравитационных зарядов.

Источник

Определение векторного поля, его характеристики, понятия, формулы и примеры (Таблица)

Основные понятия и характеристики

Формулы и поясняющие рисунки

Поле линейных скоростей вращающегося тела имеет вид:

А) векторные линии поля;

Б) дивергенцию поля;

В) циркуляцию вектора поля;

А) Имеем плоское векторное поле:

В) Будем считать, что направление нормали к плоскости совпадает с направлением оси OZ.

площадь поверхности, ограниченной кривой L.

Заметим, что если нормаль к поверхности S образует угол γ с осью OZ, то циркуляция

Ротор поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости. С точностью до числового множителя ротор поля скоростей представляет собой угловую скорость вращения твердого тела

Поток вектора через поверх­ность σ

Диверген­ция векторного поля

Связь между характерис­тиками

Циркуляция векторного поля

— радиус-вектор точки М на контуре L.

— работа силы F(M) поля при перемещении материальной точки вдоль замкнутого контура L

Ротор векторного поля

Ротор поля rot α — вектор, проекция которого на любое направление n равна поверхностной плотности циркуляции по контуру площадки, перпендикулярной к этому направлению.

Источник

Векторное поле

Ве́кторное по́ле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени различен в разных точках и может быть описан векторным полем.

Содержание

Определение и вариации [ править | править код ]

Евклидово пространство [ править | править код ]

Векторное поле на евклидовом (или псевдоевклидовом) пространстве [1] E <\displaystyle <\mathcal >> определяется как вектор-функция точки пространства, отображающая это пространство в (на) себя [2] :

Многообразие [ править | править код ]

Как сечения [ править | править код ]

Как оператор [ править | править код ]

В физике [ править | править код ]

В физике термин векторное поле, кроме общего значения, описанного выше, имеет специальное значение, в основном в отношении фундаментальных полей (см. ниже). Смысл этого употребления сводится к тому, что фундаментальные физические поля классифицируются по природе их потенциала, и один из таких типов — векторные поля (как электромагнитное или глюонное поля).

Обозначения [ править | править код ]

Обозначается векторное поле обычно просто в соответствии с соглашениями, принятыми для векторов

Достаточно обычно задание векторного поля как функции координат в пространстве, на котором поле задано, например:

или (для поля, зависящего от времени):

История термина [ править | править код ]

Термин поле (вместе с понятием силовых линий поля) (англ. field, lines of force ) ввёл в физику Майкл Фарадей около 1830 г. при исследовании электромагнитных явлений.

Основы аналитической теории силовых полей разработали Максвелл, Гиббс и Хевисайд во второй половине XIX века.

Частные случаи векторных полей [ править | править код ]

Векторные поля на прямой [ править | править код ]

Любую вещественнозначную функцию вещественного переменного можно интерпретировать как одномерное векторное поле.

Векторные поля на плоскости [ править | править код ]

Векторные поля в трёхмерном пространстве [ править | править код ]

В трёхмерном пространстве имеют смысл следующие характеристики векторного поля

Криволинейный интеграл [ править | править код ]

Циркуляция [ править | править код ]

— интеграл по замкнутому контуру:

где подынтегральное выражение совпадает с описанным чуть выше, а отличие состоит в пути интегрирования C, который в данном случае по определению замкнут, что обозначается кружком на знаке интеграла.

Поток векторного поля [ править | править код ]

Производная [ править | править код ]

Аналогом производной для векторного поля выступает тензор частных производных (якобиан), который в декартовых координатах имеет вид

Дивергенция [ править | править код ]

— след такого тензора производных. Она не зависит от системы координат (является инвариантом преобразований координат, скаляром), а в прямоугольных декартовых координатах вычисляется по формуле

Это же выражение можно записать с использованием символического оператора набла:

Теорема Остроградского — Гаусса позволяет вычислить поток векторного поля с помощью объёмного интеграла от дивергенции поля.

Ротор [ править | править код ]

— векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами

где i, j и k — единичные орты для осей x, y и z соответственно.

Для удобства запоминания можно условно представлять ротор как векторное произведение:

Градиент [ править | править код ]

— важнейшая и простейшая операция, позволяющая получить векторное поле из скалярного поля. Полученное применением такой операции к скалярному полю f векторное поле называется градиентом f:

или, записывая с помощью наблы:

Векторное поле, дивергенция которого всюду равна нулю, называется соленоидальным; оно может быть представлено как ротор некоторого другого векторного поля.

Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым); оно может быть представлено как градиент некоторого скалярного поля (потенциала).

Имеет место теорема Гельмгольца: если всюду в области D у векторного поля определены дивергенция и ротор, то это поле может быть представлено в виде суммы потенциального и соленоидального поля.

Векторное поле, у которого и дивергенция, и ротор всюду равны нулю, называется гармоническим; его потенциал представляет собой гармоническую функцию.

Векторные линии [ править | править код ]

Для силовых полей силовые линии наглядно показывают направление воздействия полевых сил.

Если в достаточно малой области пространства поле нигде не обращается в нуль, то через каждую точку этой области проходит одна и только одна силовая линия. Точки, где вектор поля нулевой — особые, в них направление поля не определено, и поведение силовых линий в окрестности этих точек может быть различным: возможно, через особую точку проходит бесконечно много силовых линий, но возможно, что не проходит ни одна.

Векторное поле называется полным, если его интегральные кривые определены на всём многообразии.

Векторные поля в n-мерном пространстве [ править | править код ]

Все перечисленные для векторных полей в трёхмерном пространстве конструкции и свойства непосредственно обобщаются на любую конечную размерность пространства n.

При этом большинство таких обобщений вполне тривиальны, за исключением определения ротора, для корректного построения которого в произвольном n-мерном случае, в отличие от трёхмерного, приходится воспользоваться внешним, а не векторным (которое определено лишь для трёхмерного случая) произведением. При n = 2 соответствующая операция принимает вид псевдоскалярного произведения.

Кроме того, в случае произвольного n нужна определённая аккуратность c определением потока. Основные определения оказываются полностью аналогичными для потока через гиперповерхность размерности (n − 1).

Физические примеры [ править | править код ]

В физике типичными примерами векторного поля являются силовые поля (силовое поле — поле некоторой силы (зависящей от положения в пространстве тела, на которое эта сила действует) или тесно связанной с силой напряжённости поля).

Исторически гидродинамика оказала огромное влияние на формирование основных конструкций векторного анализа и самой его терминологии. Так, гидродинамическое происхождение имеют такие понятия, как

а также, в той или иной мере, и многие другие (практически каждое из них имеет если не гидродинамическое происхождение, то гидродинамическую интерпретацию).

Особенности употребления термина в физике [ править | править код ]

В целом в физике термин векторное поле имеет то же значение, что и в математике, описанное выше. В этом смысле, векторным полем можно назвать любую векторнозначную физическую величину, являющуюся функцией точки пространства, зачастую зависящую также и от времени.

Однако существует и специфический случай применения этого термина, встречающийся главным образом в классификации фундаментальных физических полей. В этом случае слова «векторное поле» подразумевают, что векторным полем (4-векторное или более высокой размерности, если мы имеем дело с абстрактными многомерными теоретическими моделями) является наиболее фундаментальная величина — потенциал, а не её производные (напряженность поля и тому подобное). Так, например, к векторным полям относят электромагнитное поле, потенциал которого является 4-векторным полем, в то время как его напряженность с современной точки зрения есть тензор. Гравитационное поле называют в этом смысле тензорным, поскольку его потенциал есть тензорное поле.

Практическим синонимом слова «векторное поле» в этом смысле является в современной физике термин векторная частица (также, разводя эти близкие понятия, о векторной частице говорят как о возбуждении векторного поля, или, выражаясь несколько более традиционно — векторная частица есть квант векторного поля). Ещё один практический синоним — частица спина 1 или поле спина 1.

Из фундаментальных полей к векторным (в указанном смысле) относятся электромагнитное (фотонное), глюонное (поле сильных взаимодействий), а также поле массивных векторных бозонов — переносчиков слабого взаимодействия. Гравитационное же поле, в отличие от перечисленных, является полем тензорным.

С рассмотренной классификацией (классификацией по спину фундаментального бозонного поля) непосредственно связаны некоторые свойства соответствующего поля, например, притягиваются или отталкиваются при взаимодействии посредством этого поля частицы одинакового заряда (относящегося к данному типу взаимодействия), одинаков или противоположен такой заряд у частиц и античастиц. Частицы, взаимодействующие посредством векторного поля отталкиваются при одинаковом заряде, а притягиваются при противоположном, а пара частица — античастица имеет противоположный друг другу заряд (как, в частности, в случае электромагнитного поля) — в противоположность свойствам гравитационного поля и гравитационных зарядов.

Источник