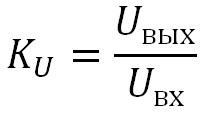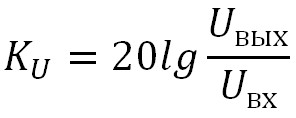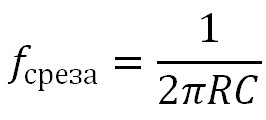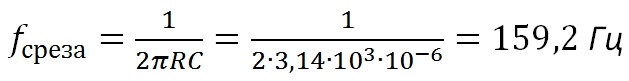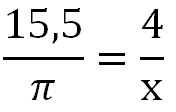максимально плоская ачх что это

Аудиофилия. И это все о ней. АЧХ.

Почему мы до сих пор спорим о качестве звука? Казалось бы все очень просто! Все свойства звука, как звуковой волны, давно изучены. Звуковоспроизводящая аппаратура все совершеннее. Но одни меломаны упорно не верят в прогресс и предпочитают проверенные временем форматы и технику. Другие уповая на технические характеристики — убеждены что нашли формулу идеального звука.

Причины, как мне кажется лежат не совсем в плоскости науки и техники. Хотя многое можно описать цифрами и формулами, кроме одной важной составляющей аудиосистемы — человека. И несмотря на то, что наука дает ответ на взаимодействие органов чувств на ощущения звука, мы все равно слышим одно и тоже по разному. В силу субъективных причин (то есть присущих определенному субъекту и не обязательно — другому) обрабатываем звуковую информацию по разному. А уж интерпретируем, вообще, «кто во что горазд»!

Глава первая: Что же такое АЧХ?

Попытаюсь внести ясность в вопрос влияния одной из самых известных и важный характеристик аудиоаппартуры — Ампилитудно частотной характеристики (далее АЧХ) на воприятие звука.

Неофиты аудиофилы или меломаны, не желающие развивать свои знания в области звука уверены, что именно АЧХ способна описать звук! И мало того, ее ширина и равномерность залог правильного звука.

Что же представляет из себя эта почитаемая аудиофилами характеристика?

Если коротко, то она описывает зависимость уровня звукового давления (то есть амплитуды) от частоты. А если совсем просто, то громкость звука определенной частоты при подачи сигнала одного уровня.

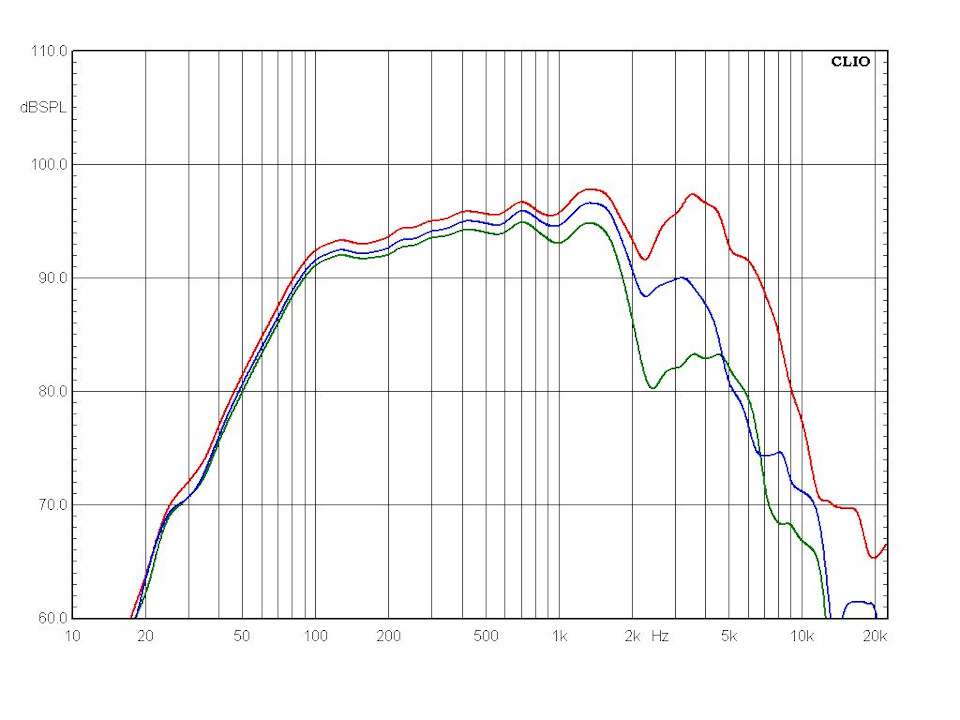
И все бы ничего если бы в реальной технике встречалась плоская и неискаженная АЧХ. Но в жизни мы видим не это:

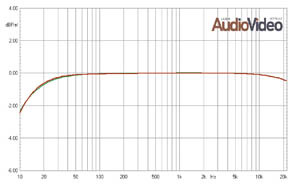
Но это АЧХ, акустических систем, воскликнет «продвинутый» читатель и будет прав! АЧХ же усилителя обычно выглядит так:

Но тем не менее даже твердолобые знают, что разные и имеющие близкие к идеальной АЧХ усилители, звучат по-разному!

Об этом в другой раз. Сейчас же о том, почему АЧХ не в состоянии до конца описать звучание.

Конечно, взаимосвязь АЧХ — звук существует, но не совсем прямая. Точнее, даже не так. Взаимосвязь «АЧХ — тональный баланс» почти линейная. Но все равно с некоторыми оговорками.

Для понимание, что ровная АЧХ и достоверное воспроизведение тембра не одно и тоже мои рассказ.

Многие ошибаясь, предполагают, что тембр это звучание сигнала определенной частоты. Нет, дорогие мои, высота звука — вот звучание сигнала определенной частоты, иначе говоря тон! А тембр это набор определенных частот (тонов и обертонов) характерных для определенного инструмента, звука.

Казалось бы, логично предположить достоверно воспроизведем весь спектр звука — достоверно воспроизведем любой тембр.

Но даже в этом есть свои сложности!

Глава вторая: Музыка не синусоида!

Основная проблема — тембр любого музыкального инструмента (мы ведь музыку будем слушать?) ни нечто статическое, а он имеет характерные только ему изменения во времени. То есть нарастания (атака) и затухания сигнала.

А это уже АЧХ не описывает! А вот аппаратура, ой как по-разному способна передавать атаку и затухание звука.

Второй важный момент — Тембр это не только основной тон, в его состав входят обертоны. То есть незначительные по уровню (по сравнению с основным тоном) тоны, характерные только для этого инструмента или голоса.

Опять же вроде ничего сложного нет, если ровно воспроизвести все частоты, то тоны и обертоны не пострадают. Но! Дело в том, что обертоны имеют отличный (более низкий) уровень по сравнению с основным. И аппаратура уже не так линейно воспроизводит сигнал меньших уровней. И чем уровень ниже, тем кривее АЧХ мы имеем.

Обычной АЧХ это тоже не описать.

Глава третья: Психоакустика — лженаука? Или обмануть меня не сложно, я сам обманываться рад!

«Технари от звука» не верят во влияние восприятия звука нашим мозгом от определенных условий. Они априори считают, что мозг это спектроанализатор и мы слышим звуки, так же как их фиксирует измерительная техника.

Но слух можно, а иногда и нужно обмануть! Например плавный и равномерный спад на краях АЧХ, то есть на высоких и низких частотах слух переносит легче и воспринимает АЧХ, как более широкую. А при резких скачках и спадах «обрезает» воспринимаемую АЧХ.

Тихие звуки маскируются более громкими. Если громкость звука резко падает, то человек на мгновение «глохнет».

Искажения на средних частотах более заметны ухом.

Так что зная эти законы (а поверьте производители их знают) можно сделать звучание компонента с более узким АЧХ не только благозвучней, но и субъективно шире, чем при прослушивании аппарата имеющего более широкую, но резко обрезанную АЧХ.

Заключение: АЧХ от Лукавого.

Получается, что АЧХ вообще не нужна? И она ничего не описывает? Если пытаться заменить «чтением» АЧХ прослушивание — несомненно! Если использовать, как инструмент дополняющий прослушивание, то почему бы и нет. Но полностью строить выводы на ее основе, как мы видим, не точнее чем предсказывать погоду. Вроде и взаимосвязь есть и опыт подсказывает, что май — не месяц снегопадов, однако реальная жизнь преподносит сюрпризы, а слух говорит о том, что криво на графиках, не всегда плохо на слух.

Источник

Аналоговые электронные устройства (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8

. (2.46)

Из (2.46) следует, что отношение токов можно варьировать в широких пределах (до двух порядков) независимо от температуры с ошибкой до 10%.

Схема имеет более высокое выходное сопротивление, чем схема на рис. 2.13, а, так как за счет резистора в транзисторе VT2 возникает ООС по току.

Если требуется получить низкое значение тока ГСТ при больших значениях опорного тока, то надо в схеме с резисторным смещением исключить резистор (=0). В этом случае и если геометрии VT1 и VT2 идентичны, то VT2 работает при более низком токе, чем VT1, т. е. >Rк. АЧХ и ПХ каскада зависят от коэффициента коррекции (рис. 3.17). При k=0.414 имеет место максимально плоская АЧХ, максимум образующейся при k>0.414, может быть использован для уменьшения частотных искажений, возникающих в других каскадах, т. е. для осуществления взаимной коррекции. При k=0.414 выигрыш по площади усиления составляет 1.72.

При L=0 ёмкость СН заряжается по экспоненциальному закону (рис. 3.18), т. к. по мере заряда ёмкости уменьшается зарядный ток за счёт ответвления части тока в сопротивление RК (и в сопротивление RН, если бы оно было соизмеримо с RК).

Индуктивность L, препятствуя возрастанию тока в цепи RK, стремится сохранить ток заряда ёмкости СН постоянным, что способствует более быстрому нарастанию на­пряжения на паразитной ёмкости.

При Q>0.5, т. е. k>0.25 переходной процесс в контуре становится колебательным, и возникают выбросы (кривая 3). Если k=0.25 выигрыш по составляет 1.36 и d=0, если k=0.35 ― 1.68 и d=1% (критический выброс), а при k=0.414 ― 1.82, d=3%.

В заключении напомню, что критическим выбросом – называется выброс, который не возрастает при увеличении числа каскадов.

3.3.4. Схема низкочастотной коррекции

АЧХ для разных значений СФ изображены на рис. 3.20. При СФ=¥ (кривая 1) резистор Rф закорочен по переменному току и мы получаем АЧХ обычного некорректированного каскада.

При СФ=0 сопротивление между точками 1-1¢ возрастает до величины Rк + Rф, что приводит к возрастанию коэффициента усиления. При Сф=const на средних частотах АЧХ каскада совпадает с кривой 1, а при низких частотах с кривой 2. Причём, при увеличении Cф средняя часть АЧХ, соединяющая линии 1 и 2, смещается влево, максимум снижается и при некотором значении Сф – исчезает.

Максимально плоская оптимальная АЧХ (кривая 4) получается при

. (3.28)

Выигрыш по уменьшению частоты среза при СP=const примерно равен

. (3.29)

Если сравнить некорректированный каскад (Сф=¥) с каскадом с оп­тимальной коррекцией (кривая 4) при одинаковой частоте среза fНС, то во втором каскаде ёмкость СР будет меньше практически в раз.

Зависимости ПХ от величины корректирующей ёмкости СФ приведены на рис.3.21. При СФ=¥ переходной процесс протекает также, как у некорректированного каскада. При СФ=0 возрастает постоянная времени и уменьшается величина спада. При СФ=const и при скачке входного напряжения заряд ёмкости СФ приводит к возрастанию напряжения на ёмкости СФ и в узле 1, что частично компенсирует спад выходного напряжения за счёт заряда СР.

Источник

Что такое АЧХ и ФЧХ

Амплитудно-частотная характеристика

Аббревиатура АЧХ расшифровывается как амплитудно-частотная характеристика. На английском этот термин звучит как «frequency response», что в дословном переводе означает «частотный отклик». Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов. АЧХ устройства определяется по зависимости коэффициента передачи (или коэффициента усиления) от частоты.

Коэффициент передачи

Что такое коэффициент передачи? Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Или формулой:

U_вых — напряжение на выходе цепи

U_вх — напряжение на входе цепи

В усилительных устройствах коэффициент передачи больше единицы. Если устройство вносит ослабление передаваемого сигнала, то коэффициент передачи меньше единицы.

Коэффициент передачи может быть выражен через децибелы:

Строим АЧХ RC-цепи в программе Proteus

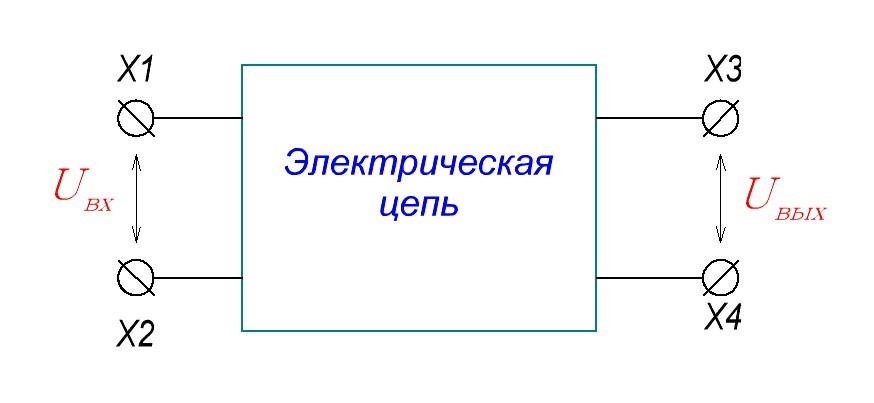
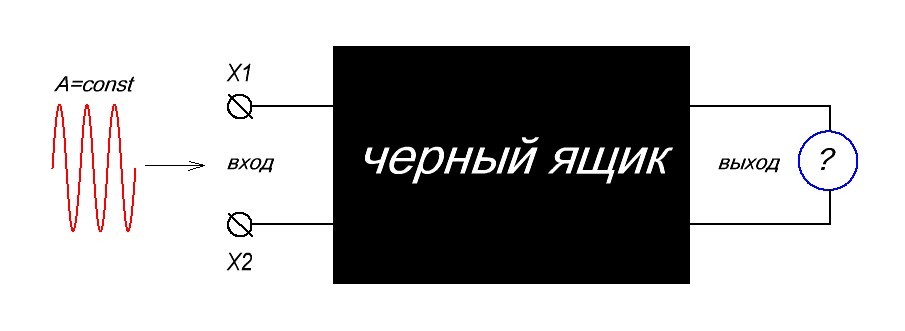
Для того, чтобы досконально разобраться, что такое АЧХ, давайте рассмотрим рисунок ниже.

Итак, имеем «черный ящик», на вход которого мы будем подавать синусоидальный сигнал, а на выходе черного ящика мы будем снимать сигнал. Должно соблюдаться условие: нужно менять частоту входного синусоидального сигнала, но его амплитуда должна быть постоянной.

Что нам делать дальше? Надо измерить амплитуду сигнала на выходе после черного ящика при интересующих нас значениях частоты входного сигнала. То есть мы должны изменять частоту входного сигнала от 0 Герц (постоянный ток) и до какого-либо конечного значения, которое будет удовлетворять нашим целям, и смотреть, какая амплитуда сигнала будет на выходе при соответствующих значениях на входе.

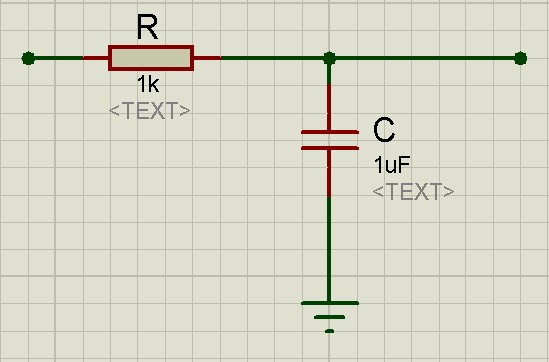
Давайте разберем все это дело на примере. Пусть в черном ящике у нас будет самая простая RC-цепь с уже известными номиналами радиоэлементов.

Как я уже говорил, АЧХ может быть построено экспериментально, а также с помощью программ-симуляторов. На мой взгляд, самый простой и мощный симулятор для новичков — это Proteus. С него и начнем.

Собираем данную схему в рабочем поле программы Proteus

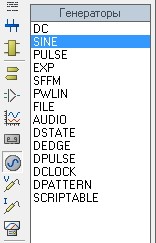
Для того, чтобы подать на вход схемы синусоидальный сигнал, мы кликаем на кнопочку «Генераторы», выбираем SINE, а потом соединяем его со входом нашей схемы.

Для измерения выходного сигнала достаточно кликнуть на значок с буквой «V» и соединить выплывающий значок с выходом нашей схемы:

Для эстетики, я уже поменял название входа и выхода на sin и out. Должно получиться как-то вот так:

Ну вот, пол дела уже сделано.

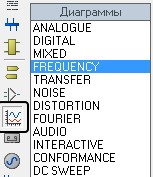
Теперь осталось добавить важный инструмент. Он называется «frequency response», как я уже говорил, в дословном переводе с английского — «частотный отклик». Для этого нажимаем кнопочку «Диаграмма» и в списке выбираем «frequency»

На экране появится что-то типа этого:

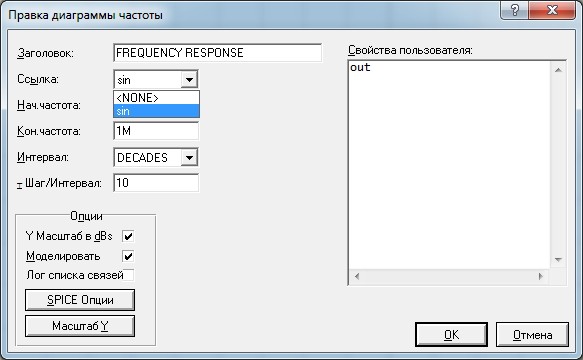
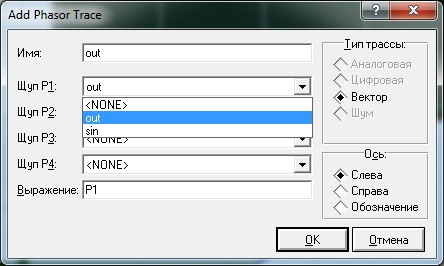
Кликаем ЛКМ два раза и открывается вот такое окошко, где в качестве входного сигнала мы выбираем наш генератор синуса (sin), который у нас сейчас задает частоту на входе.

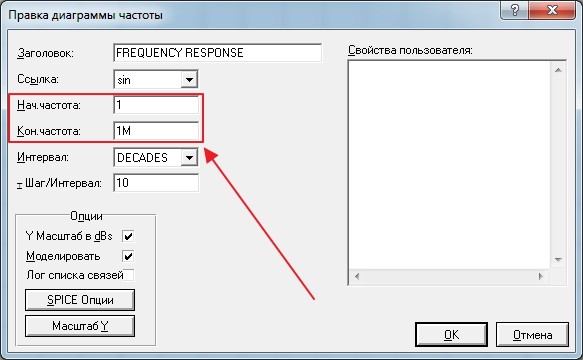
Здесь же выбираем диапазон частоты, который будем «загонять» на вход нашей цепи. В данном случае это диапазон от 1 Гц и до 1 МГц. При установке начальной частоты в 0 Герц Proteus выдает ошибку. Поэтому, ставьте начальную частоту близкую к нулю.

Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

Долго не думая, выбираем в первом же окошке наш выход out

и в результате должно появится окошко с нашим выходом

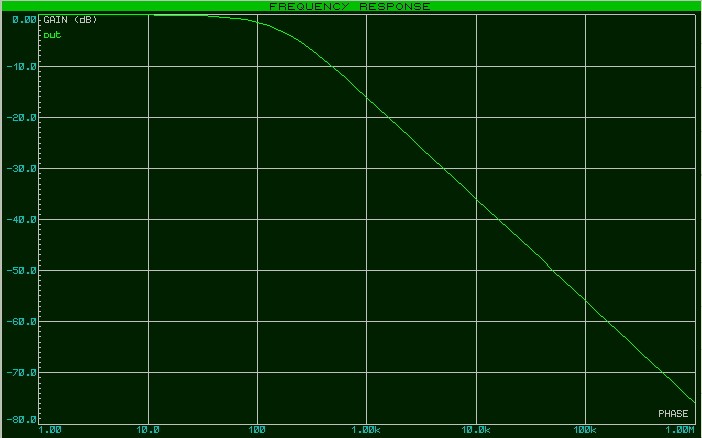
Нажимаем пробел и радуемся результату

Итак, что интересного можно обнаружить, если взглянуть на нашу АЧХ? Как вы могли заметить, амплитуда на выходе цепи падает с увеличением частоты. Это означает, что наша RC-цепь является своеобразным частотным фильтром. Такой фильтр пропускает низкие частоты, в нашем случае до 100 Герц, а потом с ростом частоты начинает их «давить». И чем больше частота, тем больше он ослабляет амплитуду выходного сигнала. Поэтому, в данном случае, наша RC-цепь является самым простейшим фильтром низкой частоты (ФНЧ).

Полоса пропускания

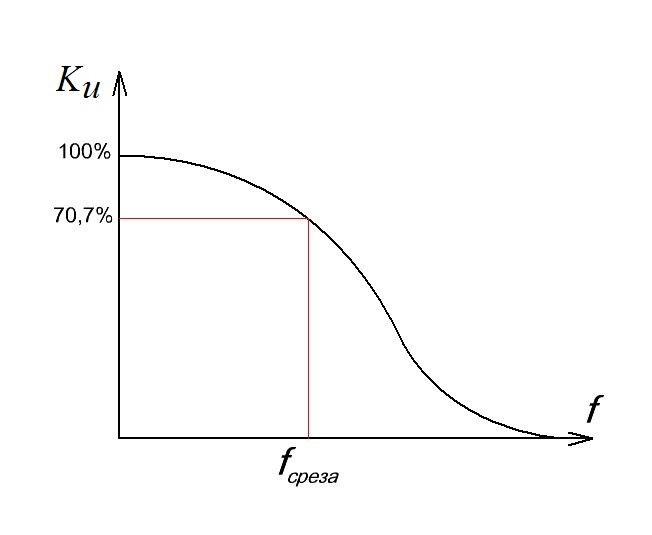
В среде радиолюбителей и не только встречается также такой термин, как полоса пропускания. Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы.

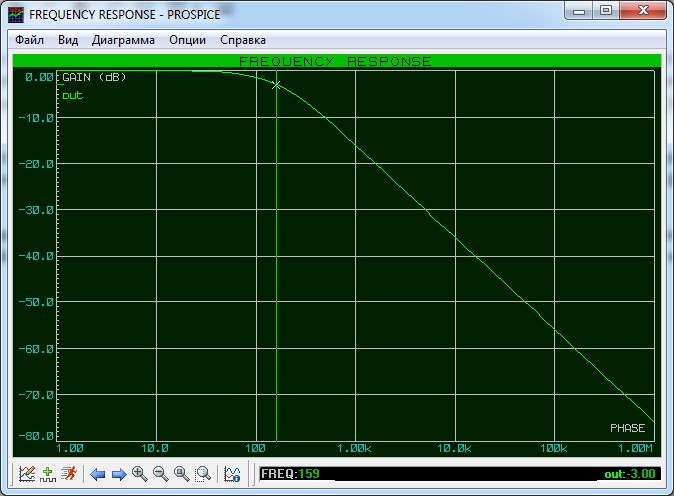
Для нашего случая расчетная частота получилась 159,2 Гц, что подтверждает и Proteus.

Кто не желает связываться с децибелами, то можно провести линию на уровне 0,707 от максимальной амплитуды выходного сигнала и смотреть пересечение с графиком. В данном примере, для наглядности, я взял максимальную амплитуду за уровень в 100%.

Как построить АЧХ на практике?

Как построить АЧХ на практике, имея в своем арсенале генератор частоты и осциллограф?

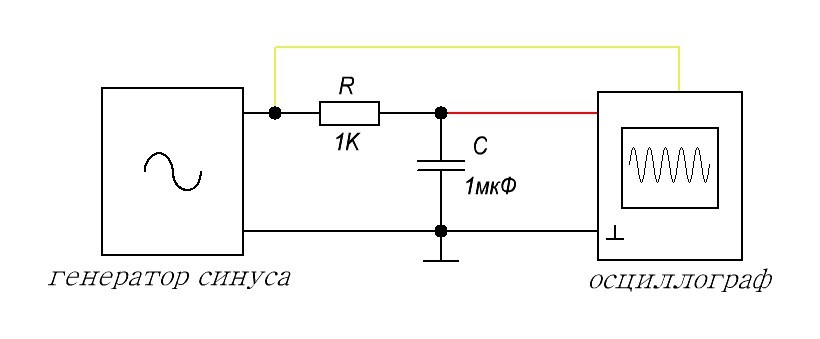
Итак, поехали. Собираем нашу цепь в реале:

Ну а теперь цепляем ко входу схемы генератор частоты, а с помощью осциллографа следим за амплитудой выходного сигнала, а также будем следить за амплитудой входного сигнала, чтобы мы были точно уверены, что на вход RC-цепи подается синус с постоянной амплитудой.

Для экспериментального изучения АЧХ нам потребуется собрать простенькую схемку:

Наша задача состоит в том, чтобы менять частоту генератора и уже наблюдать, что покажет осциллограф на выходе цепи. Мы будем прогонять нашу цепь по частотам, начиная от самой малой. Как я уже сказал, желтый канал предназначен для визуального контроля, что мы честно проводим опыт.

Постоянный ток, проходящий через эту цепь, на выходе будет давать амплитудное значение входного сигнала, поэтому первая точка будет иметь координаты (0;4), так как амплитуда нашего входного сигнала 4 Вольта.

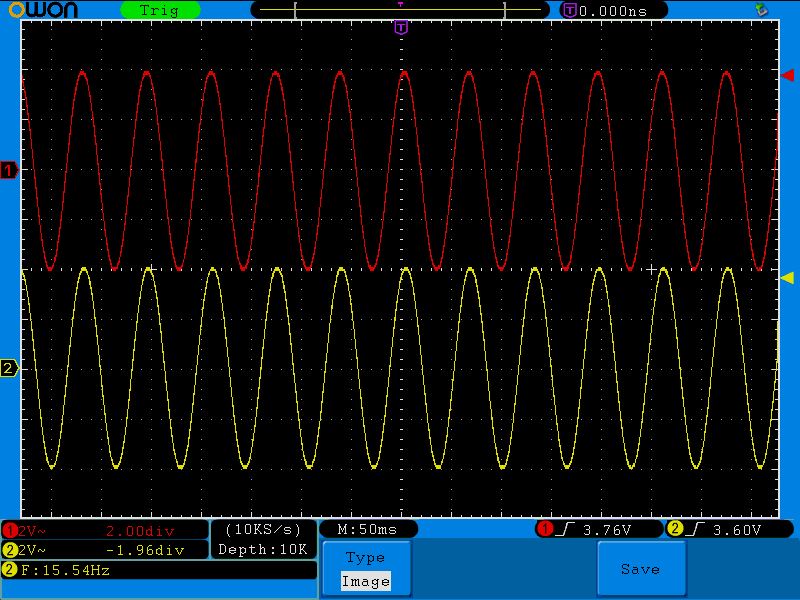
Следующее значение смотрим на осциллограмме:

Частота 15 Герц, амплитуда на выходе 4 Вольта. Итак, вторая точка (15;4)

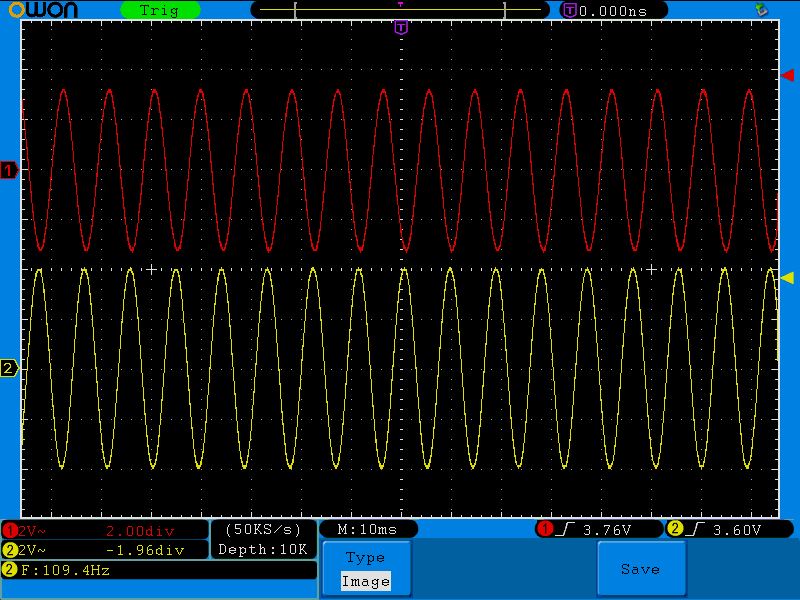
Третья точка (72;3.6). Обратите внимание на амплитуду выходного красного сигнала. Она начинает проседать.

Четвертая точка (109;3.2)

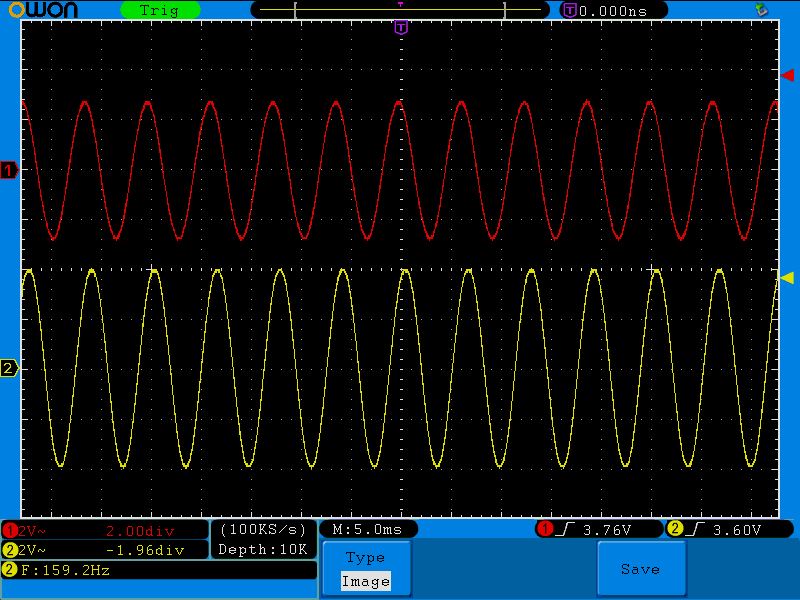
Шестая точка (201;2.4)

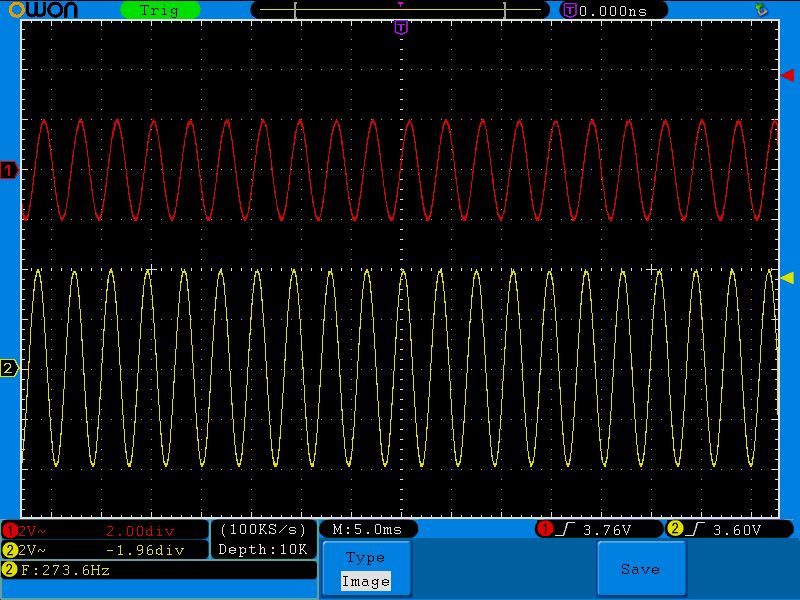
Седьмая точка (273;2)

Восьмая точка (361;1.6)

Девятая точка (542;1.2)

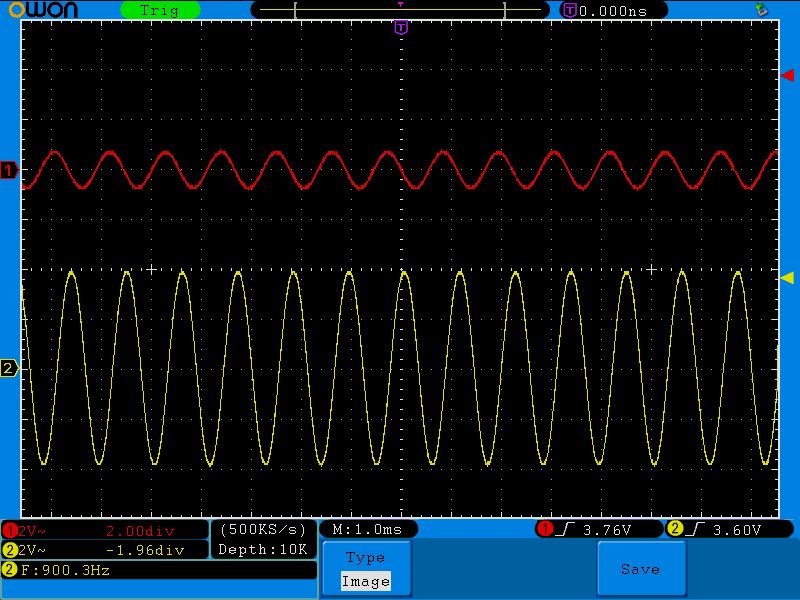
Десятая точка (900;0.8)

Ну и последняя одиннадцатая точка (1907;0.4)

В результате измерений у нас получилась табличка:

Строим график по полученным значениям и получаем нашу экспериментальную АЧХ 😉

Получилось не так, как в технической литературе. Оно и понятно, так как по Х берут логарифмический масштаб, а не линейный, как у меня на графике. Как вы видите, амплитуда выходного сигнала будет и дальше понижаться с увеличением частоты. Для того, чтобы еще более точно построить нашу АЧХ, требуется взять как можно больше точек.

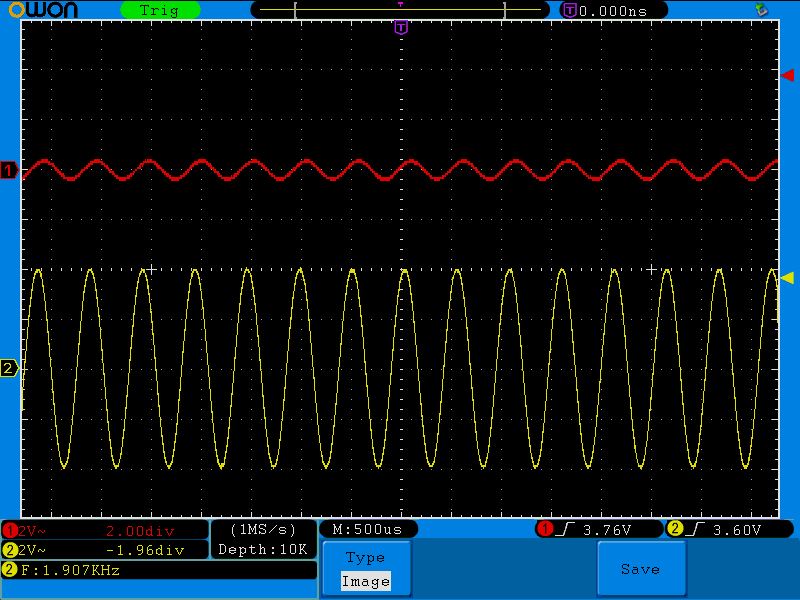
Давайте вернемся к этой осциллограмме:

Здесь на частоте среза амплитуда выходного сигнала получилась ровно 2,8 Вольт, которые как раз и находятся на уровне в 0,707. В нашем случае 100% это 4 Вольта. 4х0,707=2,82 Вольта.

АЧХ полосового фильтра

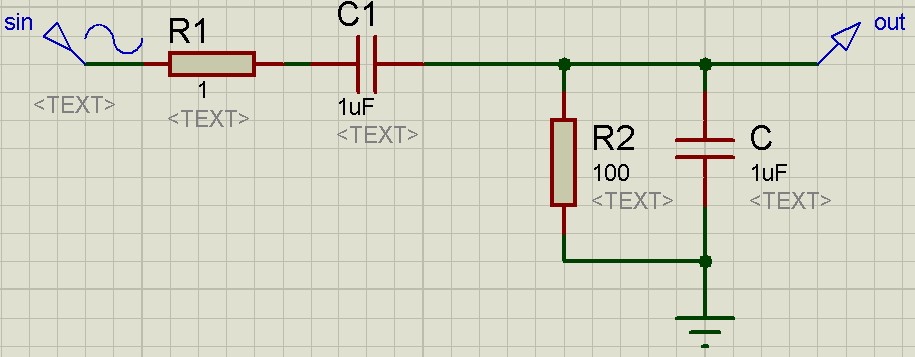
Существуют также схемы, АЧХ которых имеет вид холма или ямы. Давайте рассмотрим один из примеров. Мы будем рассматривать так называемый полосовой фильтр, АЧХ которого имеет вид холма.

Собственно сама схема:

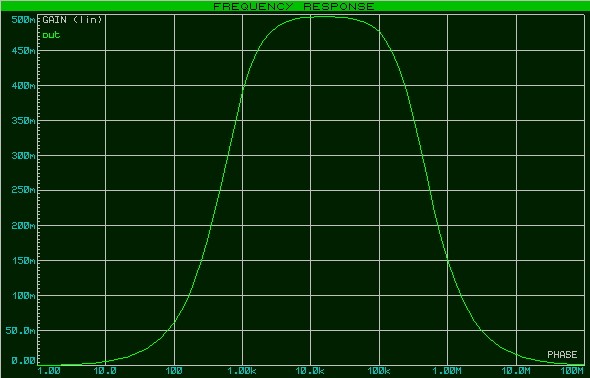
Так как в дБ смотреть график неудобно, поэтому я переведу его в линейный режим по оси Y, убирая маркер

В результате перестроения получилась такая АЧХ:

Максимальное значение на выходе составило 498 мВ при амплитуде входного сигнала в 10 Вольт. Мдя, неплохой «усилитель») Итак, находим значение частот на уровне в 0,707х498=352мВ. В результате получились две частоты среза — это частота в 786 Гц и в 320 КГц. Следовательно, полоса пропускания данного фильтра от 786Гц и до 320 КГц.

На практике для получения АЧХ используются приборы, называемые характериографами для исследования АЧХ. Вот так выглядит один из образцов Советского Союза

Фазо-частотная характеристика

ФЧХ расшифровывается как фазо-частотная характеристика, phase response — фазовый отклик. Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

Разность фаз

Думаю, вы не раз слышали такое выражение, как » у него произошел сдвиг по фазе». Это выражение не так давно пришло в наш лексикон и обозначает оно то, что человек слегка двинулся умом. То есть было все нормально, а потом раз! И все :-). И в электронике такое тоже часто бывает) Разницу между фазами сигналов в электронике называют разностью фаз. Вроде бы «загоняем» на вход какой-либо сигнал, а выходной сигнал ни с того ни с сего взял и сдвинулся по времени, относительно входного сигнала.

Для того, чтобы определить разность фаз, должно выполняться условие: частоты сигналов должны быть равны. Пусть даже один сигнал будет с амплитудой в Киловольт, а другой в милливольт. Неважно! Лишь бы соблюдалось равенство частот. Если бы условие равенства не соблюдалось, то сдвиг фаз между сигналами все время бы изменялся.

Для определения сдвига фаз используют двухканальный осциллограф. Разность фаз чаще всего обозначается буквой φ и на осциллограмме это выглядит примерно так:

Строим ФЧХ RC-цепи в Proteus

Для нашей исследуемой цепи

Для того, чтобы отобразить ее в Proteus мы снова открываем функцию «frequency response»

Все также выбираем наш генератор

Не забываем проставлять испытуемый диапазон частот:

Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»

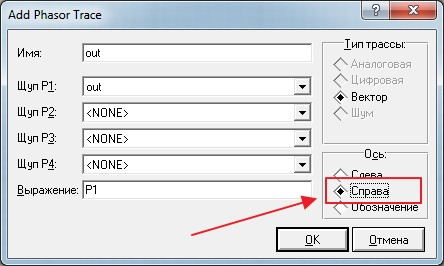
Долго не думая, выбираем в первом же окошке наш выход out

И теперь главное отличие: в колонке «Ось» ставим маркер на «Справа»

Нажимаем пробел и вуаля!

Можно его развернуть на весь экран

При большом желании эти две характеристики можно объединить на одном графике

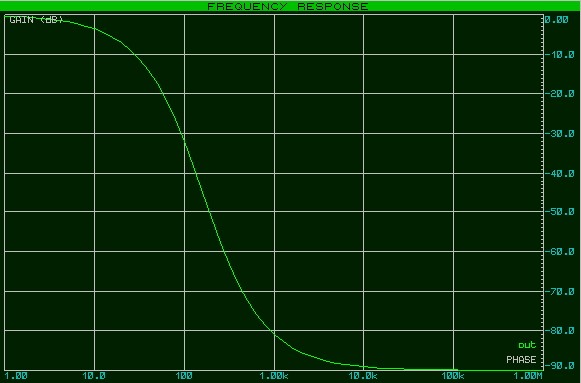
Обратите внимание, что на частоте среза сдвиг фаз между входным и выходным сигналом составляет 45 градусов или в радианах п/4 (кликните для увеличения)

В данном опыте при частоте более 100 КГц разность фаз достигает значения в 90 градусов (в радианах π/2) и уже не меняется.

Строим ФЧХ на практике

ФЧХ на практике можно измерить также, как и АЧХ, просто наблюдая разность фаз и записывая показания в табличку. В этом опыте мы просто убедимся, что на частоте среза у нас действительно разность фаз между входным и выходным сигналом будет 45 градусов или π/4 в радианах.

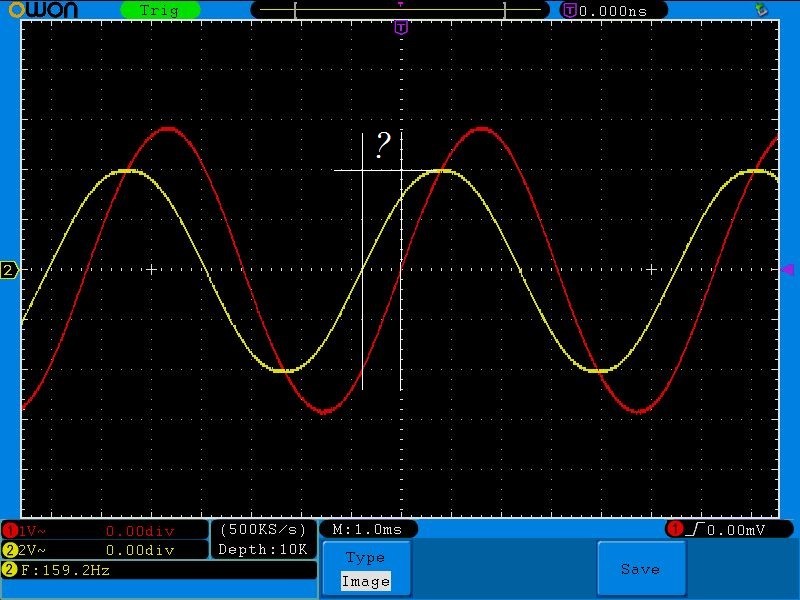
Итак, у меня получилась вот такая осциллограмма на частоте среза в 159,2 Гц

Нам надо узнать разность фаз между этими двумя сигналами

Весь период — это 2п, значит половина периода — это π. На полупериод у нас приходится где-то 15,5 делений. Между двумя сигналами разность в 4 деления. Составляем пропорцию:

Отсюда х=0,258п или можно сказать почти что 1/4п. Следовательно, разница фаз между двумя этими сигналами равняется п/4, что почти в точности совпало с расчетными значениями в Proteus.

Если Вы лучше воспринимаете информацию через видео, то к Вашему вниманию:

Резюме

Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства.

Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Если коэффициент передачи больше единицы, то электрическая цепь усиливает входной ссигнал, если же меньше единицы, то ослабляет.

Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы. Определяется по уровню 0,707 от максимального значения АЧХ.

Источник