Как построить жорданову форму матрицы
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Жорданова нормальная форма
Жорданова нормальная форма над полем комплексных чисел
Общая схема
Аннулирующий полином
Теорема 5. Минимальный аннулирующий полином оператора является делителем его характеристического полинома. Два минимальных аннулирующих полинома оператора различаются, разве лишь, постоянным множителем.
Следствиями теорем 4 и 5 является следующий результат.
Корневое подпространство
Рассмотрим теперь пример, разобранный в ☞ ПУНКТЕ.
Пример 3. Найти корневые векторы матрицы
Доказательство. Следствие теоремы 2. ♦
Алгоритм построения базиса корневого подпространства
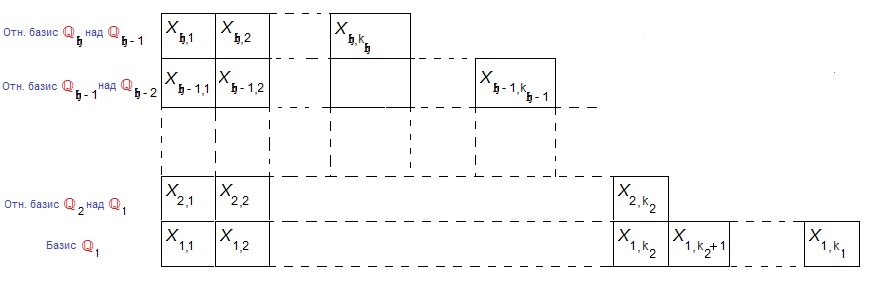
Для визуализации последующего алгоритма построения канонического базиса удобно представить результаты этого этапа в виде схемы:
Мы наблюдаем разноэтажное здание, число квартир на каждом этаже которого не превосходит числа квартир на предыдущем. В ходе дальнейшего алгоритма, часть «жильцов» останется на месте, а часть может быть замещена другими.
4. Продолжаем процесс…
Структура соответствующего канонического базиса
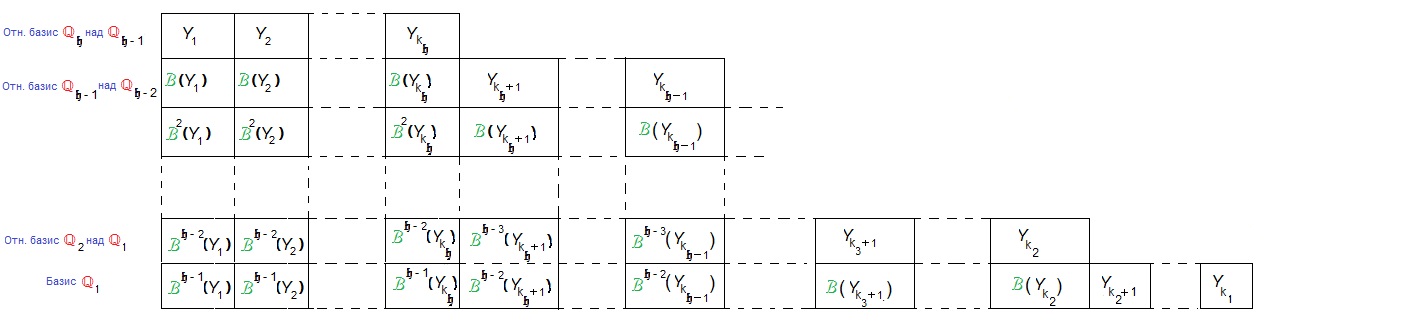
В каноническом базисе корневые векторы, соответствующие указанной последовательности клеток, следует упорядочить по следующему правилу:
Объяснение необходимости перестановки векторов канонического базиса — почему они нумеруются по правилу «сверху вниз», а не поэтажно — дается в следующем ПУНКТЕ.
Пример 3 (окончание). Построить ЖНФ и канонический базис пространства для оператора из примера 3.
Циклическое подпространство
Теорема 11. Пусть система
Построить ЖНФ и канонический базис для оператора из примера 2.
Жорданова нормальная форма над полем вещественных чисел
Жорданова форма
Жорданова форма матрицы определена не однозначно, а с точностью до порядка жордановых клеток. Точнее, две жордановы матрицы подобны над k в том и только в том случае, когда они составлены из одних и тех же жордановых клеток и отличаются друг от друга лишь расположением этих клеток на главной диагонали.
Помимо жордановой нормальной формы, рассматривают ряд других типов нормальных форм матрицы. К их рассмотрению прибегают, например, когда основное поле не содержит всех корней минимального многочлена матрицы.
Свойства
История
Такая форма матрицы рассматривалась одним из первых Жорданом.
Полезное
Смотреть что такое «Жорданова форма» в других словарях:
Нормальная (жорданова) форма матриц — Нормальная (жорданова) форма матриц. С каждой квадратной матрицей связан целый класс матриц, подобных матрице А. В этом классе всегда существует матрица, имеющая специальную нормальную (или каноническую) жорданову форму [термин «Н. (ж.) ф. м.»… … Большая советская энциклопедия
Жорданова нормальная форма — Жорданова матрица квадратная блочно диагональная матрица над полем k, с блоками вида … Википедия
ЖОРДАНОВА МАТРИЦА — квадратная блочно диагональная матрица J над полем к, имеющая вид где Jm(l) квадратная матрица порядка твида Матрица J т(l)называется жордановой клеткой порядка m с собственным числом к. Каждая клетка определяется элементарным делителем (см. [5]) … Математическая энциклопедия
жорданова нормальная форма — Jordano norminė forma statusas T sritis automatika atitikmenys: angl. Jordan canonical form; Jordan normal form vok. Jordansche Normalform, f; Kanonische Jordanform, f rus. жорданова нормальная форма, f; каноническая форма Жордана, f pranc. forme … Automatikos terminų žodynas
ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА — матрицы см. Жорданова матрица … Математическая энциклопедия
Нормальная форма матриц — (жорданова) С каждой квадратной матрицей (См. Матрица) А. В этом классе всегда существует матрица, имеющая специальную нормальную (или каноническую) жорданову форму [термин «Н. (ж.) ф. м.» связан с именем К. Жордана]. На схеме показана… … Большая советская энциклопедия
Нормальная форма (математика) — У этого термина существуют и другие значения, см. Нормальная форма (значения). Нормальная форма в математике простейший либо канонический вид, к которому объект приводится эквивалентными преобразованиями[1]. Содержание 1 Жорданова… … Википедия
Нормальная форма (значения) — Нормальная форма: Нормальная форма в базах данных свойство отношения в реляционной модели данных. Нормальная форма в математике в каком либо смысле простейший либо канонический вид, к которому объект приводится преобразованиями,… … Википедия
Жорданова нормальная форма
Жорданова форма матрицы определена не однозначно, а с точностью до порядка жордановых клеток. Точнее, две жордановы матрицы подобны над k в том и только в том случае, когда они составлены из одних и тех же жордановых клеток и отличаются друг от друга лишь расположением этих клеток на главной диагонали.
Помимо жордановой нормальной формы, рассматривают ряд других типов нормальных форм матрицы. К их рассмотрению прибегают, например, когда основное поле не содержит всех корней минимального многочлена матрицы.
Свойства
История
Такая форма матрицы рассматривалась одним из первых Жорданом.
Полезное
Смотреть что такое «Жорданова нормальная форма» в других словарях:
жорданова нормальная форма — Jordano norminė forma statusas T sritis automatika atitikmenys: angl. Jordan canonical form; Jordan normal form vok. Jordansche Normalform, f; Kanonische Jordanform, f rus. жорданова нормальная форма, f; каноническая форма Жордана, f pranc. forme … Automatikos terminų žodynas
ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА — матрицы см. Жорданова матрица … Математическая энциклопедия
Нормальная форма (математика) — У этого термина существуют и другие значения, см. Нормальная форма (значения). Нормальная форма в математике простейший либо канонический вид, к которому объект приводится эквивалентными преобразованиями[1]. Содержание 1 Жорданова… … Википедия
Нормальная форма (значения) — Нормальная форма: Нормальная форма в базах данных свойство отношения в реляционной модели данных. Нормальная форма в математике в каком либо смысле простейший либо канонический вид, к которому объект приводится преобразованиями,… … Википедия
Нормальная форма матриц — (жорданова) С каждой квадратной матрицей (См. Матрица) А. В этом классе всегда существует матрица, имеющая специальную нормальную (или каноническую) жорданову форму [термин «Н. (ж.) ф. м.» связан с именем К. Жордана]. На схеме показана… … Большая советская энциклопедия
ЖОРДАНОВА МАТРИЦА — квадратная блочно диагональная матрица J над полем к, имеющая вид где Jm(l) квадратная матрица порядка твида Матрица J т(l)называется жордановой клеткой порядка m с собственным числом к. Каждая клетка определяется элементарным делителем (см. [5]) … Математическая энциклопедия
Нормальная (жорданова) форма матриц — Нормальная (жорданова) форма матриц. С каждой квадратной матрицей связан целый класс матриц, подобных матрице А. В этом классе всегда существует матрица, имеющая специальную нормальную (или каноническую) жорданову форму [термин «Н. (ж.) ф. м.»… … Большая советская энциклопедия
каноническая форма Жордана — Jordano norminė forma statusas T sritis automatika atitikmenys: angl. Jordan canonical form; Jordan normal form vok. Jordansche Normalform, f; Kanonische Jordanform, f rus. жорданова нормальная форма, f; каноническая форма Жордана, f pranc. forme … Automatikos terminų žodynas
СОДЕРЖАНИЕ
Обзор
Обозначение
В некоторых учебниках есть поддиагональ ; то есть непосредственно под главной диагональю, а не на наддиагонали. Собственные значения по-прежнему находятся на главной диагонали.
Мотивация
Комплексные матрицы
где каждый блок J i представляет собой квадратную матрицу вида
Предполагая этот результат, мы можем вывести следующие свойства:
Пример
Пример: получение нормальной формы
В этом примере показано, как вычислить нормальную форму Жордана данной матрицы.
о котором упоминается в начале статьи.
Вычисление показывает, что уравнение P −1 AP = J действительно выполняется.
Обобщенные собственные векторы
Доказательство
В противном случае, если
Уникальность
Можно показать, что жорданова нормальная форма данной матрицы A единственна с точностью до порядка жордановых клеток.
равно удвоенному количеству жордановых блоков размера k 1 плюс количество жордановых блоков размера k 1 −1. Общий случай аналогичен.
Реальные матрицы
и описать умножение на в комплексной плоскости. Наддиагональные блоки представляют собой единичные матрицы 2 × 2 и, следовательно, в этом представлении размерности матрицы больше, чем у комплексной жордановой формы. Полный реальный блок Джордана дается формулой λ я <\ displaystyle \ lambda _ >
Эта вещественная жорданова форма является следствием комплексной жордановой формы. Для действительной матрицы невещественные собственные векторы и обобщенные собственные векторы всегда можно выбрать для образования комплексно сопряженных пар. Взяв действительную и мнимую части (линейную комбинацию вектора и сопряженного с ним), матрица имеет такой вид относительно нового базиса.
Матрицы с записями в поле
Последствия
Можно видеть, что нормальная форма Жордана является, по сути, результатом классификации квадратных матриц, и поэтому несколько важных результатов линейной алгебры можно рассматривать как ее следствия.
Теорема о спектральном отображении
Характеристический полином
Теорема Кэли – Гамильтона
Минимальный многочлен
Инвариантные разложения подпространств
Можно также получить несколько иное разложение с помощью жордановой формы. Для заданного собственного значения λ i размер его наибольшего соответствующего жорданова блока s i называется индексом λ i и обозначается ν (λ i ). (Следовательно, степень минимального многочлена равна сумме всех индексов.) Определим подпространство Y i следующим образом:
Это дает разложение
Здесь может быть интересно отметить некоторые свойства индекса ν ( λ ). В более общем смысле, для комплексного числа λ его индекс может быть определен как наименьшее неотрицательное целое число ν (λ) такое, что
Плоская (плоская) нормальная форма
Жорданова форма используется для нахождения нормальной формы матриц с точностью до сопряжения, такой что нормальные матрицы составляют алгебраическое многообразие низкой фиксированной степени в пространстве объемлющих матриц.
Множества представителей классов матричной сопряженности для жордановой нормальной формы или рациональных канонических форм в общем случае не составляют линейных или аффинных подпространств в объемных матричных пространствах.
Для алгебраически замкнутых полей она была решена Петерисом Даугулисом. Построение однозначно определенной плоской нормальной формы матрицы начинается с рассмотрения ее жордановой нормальной формы.
Матричные функции
Итерация цепочки Джордана мотивирует различные расширения к более абстрактным параметрам. Для конечных матриц получаются матричные функции; это может быть распространено на компактные операторы и голоморфное функциональное исчисление, как описано ниже.
В следующем примере показано приложение к степенной функции f ( z ) = z n :
Компактные операторы
Голоморфное функциональное исчисление
Нам потребуются следующие свойства этого функционального исчисления:
Конечномерный случай
Теорема о спектральном отображении говорит нам
имеет спектр <0>. По свойству 1 f ( T ) может быть непосредственно вычислено в жордановой форме, и, проверив, мы видим, что оператор f ( T ) e i ( T ) является нулевой матрицей.
Поляки оператора
Точка λ называется полюсом оператора T порядка ν, если резольвентная функция R T, определенная равенством
имеет полюс порядка ν в точке λ.
Мы покажем, что в конечномерном случае порядок собственного значения совпадает с его индексом. Результат верен и для компактных операторов.
Согласно предыдущему обсуждению функционального исчисления,
Но мы показали, что наименьшее натуральное число m такое, что
в точности индекс λ, ν (λ). Другими словами, функция R T имеет полюс порядка ν (λ) в точке λ.
Числовой анализ
Если матрица A имеет несколько собственных значений или близка к матрице с несколькими собственными значениями, то ее жорданова нормальная форма очень чувствительна к возмущениям. Рассмотрим, например, матрицу
Если ε = 0, то нормальная форма Жордана просто
Однако при ε ≠ 0 жорданова нормальная форма имеет вид