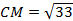Как построить угол зная косинус
Уроки математики и физики для школьников и родителей
понедельник, 27 сентября 2021 г.
Урок 10. Построение угла по данному значению его тригонометрической функции
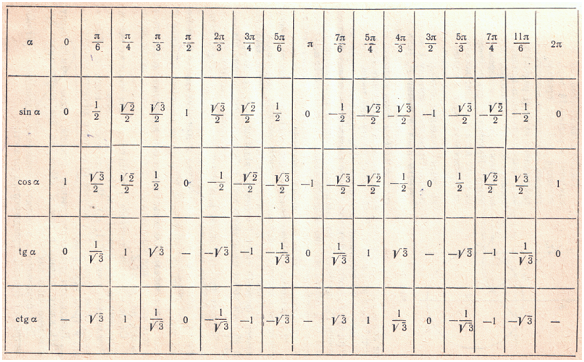
Изменение тригонометрических функций с изменением угла от 0 ° до 90 ° .
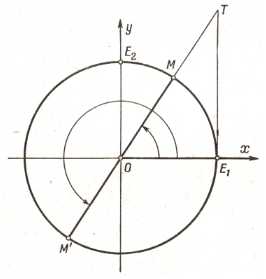
Рассмотрим окружность произвольного радиуса с центром в точке А.
Построим соответствующие этим положениям радиуса прямоугольные треугольники:
Чтобы проследить за изменением тангенса острого угла, возьмём прямоугольный треугольник АВС
следовательно, возрастает и tg α так как катет АС остаётся без изменения.
Построение угла по данному значению его тригонометрической функции с помощью острого угла.
Из определения sin α и cos α следует, что синус и косинус острого угла α – положительные числа, меньшие единицы.
где α – острый угол.
Каково бы ни было положительное число у , меньшее единицы, существует, и притом только один, острый угол α , синус которого равен у :
Каково бы ни было положительное число р , существует, и притом только один, острый угол α , тангенс которого равен р :
На одной стороне прямого угла МО N,
Каково бы ни было положительное число q , существует, и притом только один, острый угол α , котангенс которого равен q :
Построить угол α , котангенс которого равен 3 .
На сторонах прямого угла LKM,
Выражение тригонометрических функций через одну из них с помощью острого угла.
Найдём значение синуса, косинуса, тангенса и котангенса угла
Таким же путём можно найти приближённые значения синуса, косинуса, тангенса и котангенса любого острого угла.
При этом степень приближения будет зависеть только от точности наших измерений.
Построение углов по данному значению его тригонометрической функции с помощью единичной окружности.
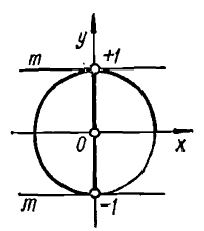
Построить угол (дугу) α , синус которого равен m .
Рассмотрим три случая.
На положительной оси Ох откладываем от точки О отрезок, равный 3 / 4 радиуса единичной окружности.
Введём на плоскости прямоугольную систему координат.
Построить углы α , для которых tg α = 1,5 .
Геометрический вывод значений тригонометрических функций.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
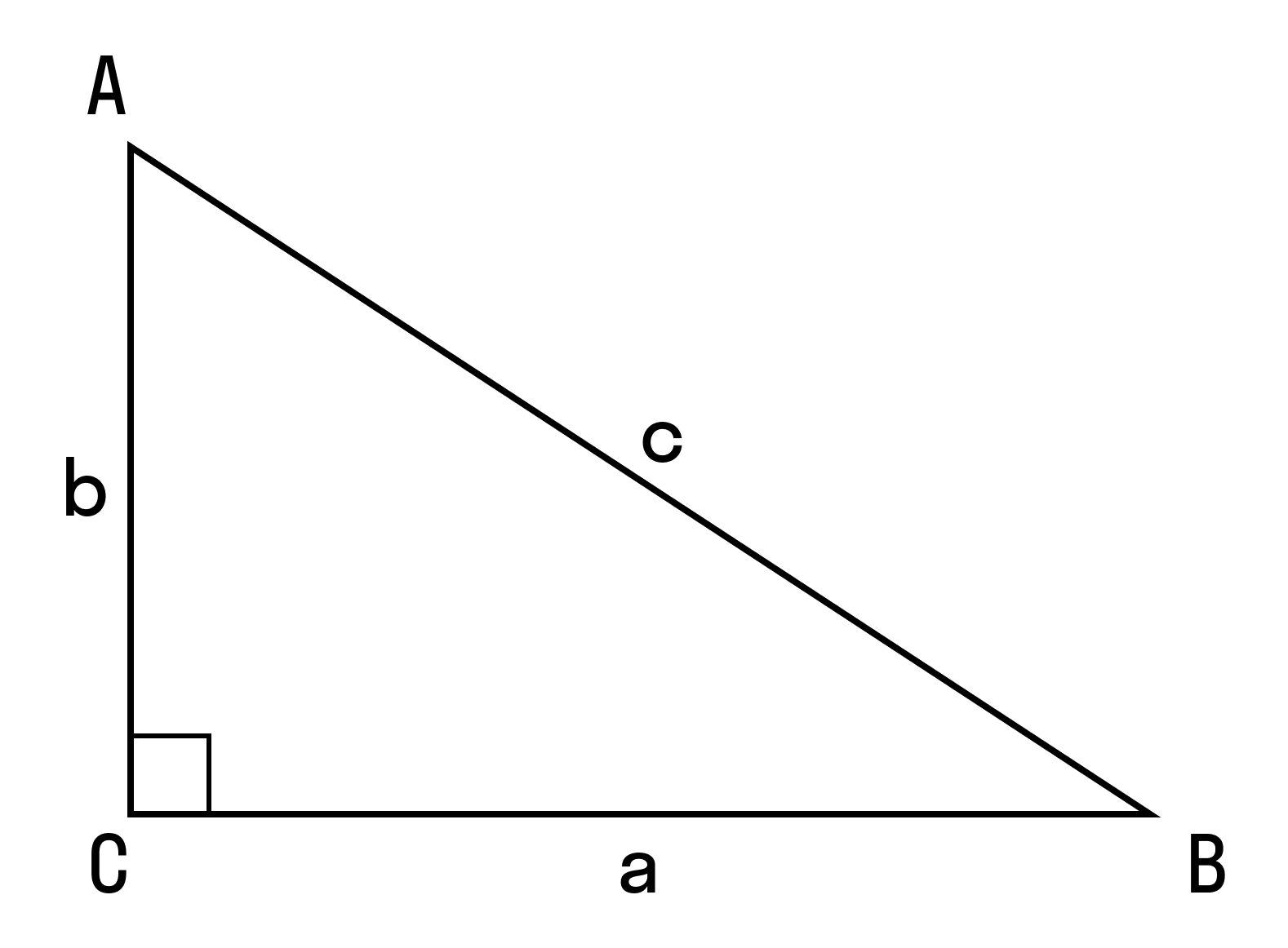
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Теорема косинусов и синусов
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений:
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
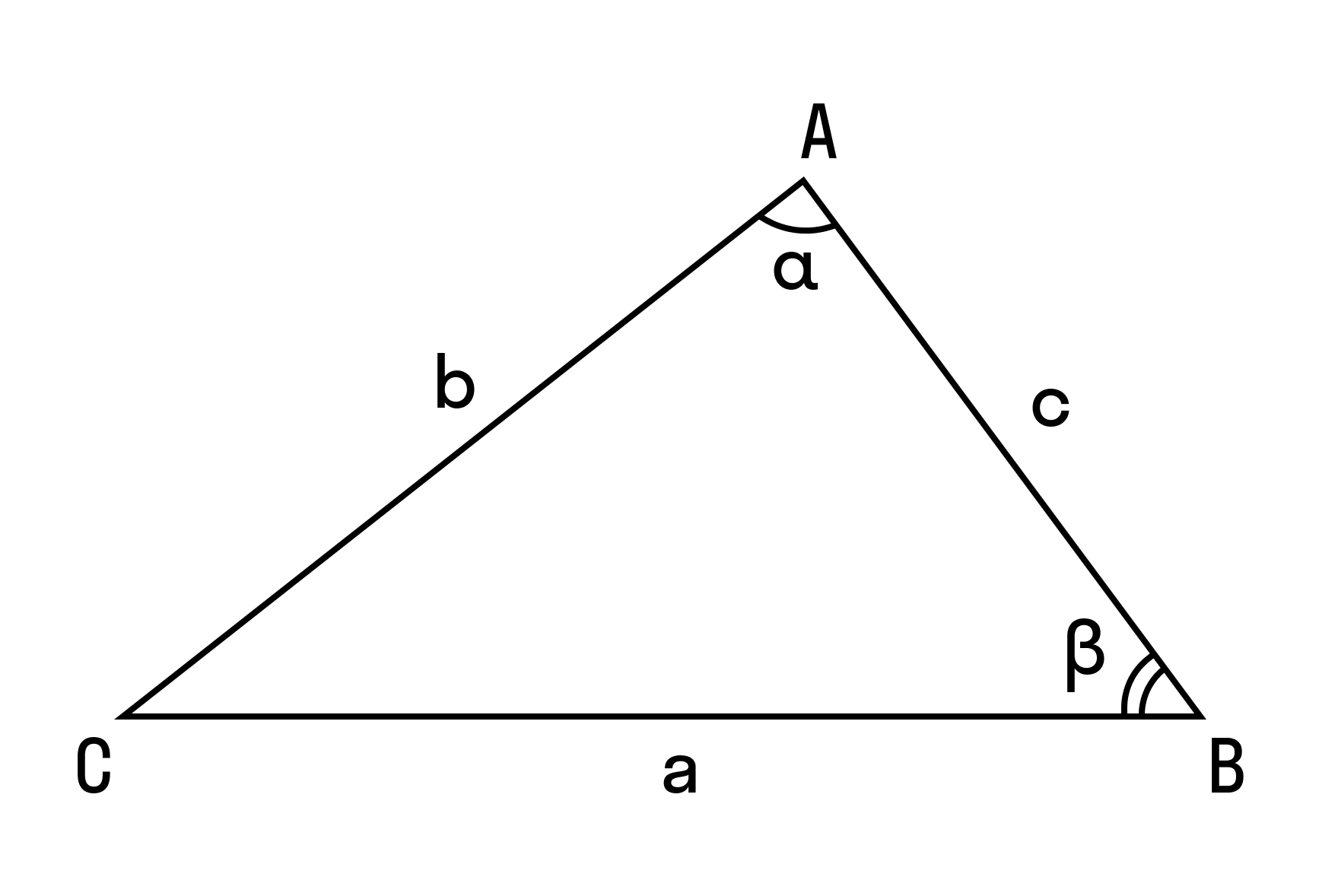
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Синус и косинус угла на единичной окружности
Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:
С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что
ВС = АВ•sinα = 5•0,8 = 4
Если известно, что cosα = 0,6, то мы сможем найти и второй катет:
АС = АВ•cosα = 5•0,6 = 3
Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:
tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)
Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты хА и уА:
Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:
Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле
Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда
АВ = sinα•ОА = sinα•1 = sinα
С другой стороны, видно, что величина отрезка АВ равна координате уА. Получается, что уА = АВ = sinα, или
Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:
Учитывая, что ОА = 1, а длина ОВ равна координате хА, мы получим следующее:
хА = ОВ = cosα•ОА = cosα•1 = cosα
то есть координата хА равна cos α:
Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.
Таким образом, нам удалось дать новое определение синусу и косинусу угла:
Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть
Презентация была опубликована 8 лет назад пользователемДарья Наточиева
Похожие презентации
Презентация на тему: » Синус, косинус и тангенс угла Подготовила: учитель математики МОУ сош 30 имени А.И.Колдунова Кутоманова Е.М. 2010-2011 учебный год.» — Транскрипт:
1 Синус, косинус и тангенс угла Подготовила: учитель математики МОУ сош 30 имени А.И.Колдунова Кутоманова Е.М учебный год
2 1.Определение тригонометрических функций Синусом угла называется отношение противолежащего катета к гипотенузе: sin = ВС:АВ Косинусом угла называется отношение прилежащего катета к гипотенузе: cos = АС:АВ Тангенсом угла называется отношение противолежащего катета к прилежащему: tg = ВС:АС Котангенсом угла называется отношение прилежащего катета к противолежащему: ctg = АС:ВС Пример. Дано:а = 5, b = 12, c = 13. Найти: sinA, cosA, tgA, ctgA Решение: sinA = а:с, sinA = 5:13, cosA = в:с, cosA = 12:13, tgA = а:в, tgA = 5:12, ctgA = в:а, ctgA = 12:5. AC B
3 2.Синус, косинус, тангенс Введём прямоугольную систему координат Оху. Построим полуокружность с центром в начале координат и радиусом, равным 1. Эту полуокружность назовём единичной полуокружностью. α-угол между лучом h и положительной полуосью Ох. Из ΔОМD-прямоугольного имеем: sinα=МD:ОМ, соsα=ОD:ОМ. Т.к. ОМ=1, МD=у, ОD=х, то sinα=у, соsα=х. Выполним у С (0;1) h М(х,у)М(х,у) В (-1;0) 0 α D А (1;0) х
5 Тангенсом угла α называется отношение sinα к соsα, т.е.tgα=sinα:соsα. При α=90° tgα не определён, т.к. соs90°=0. Т.к. sin0°=0 и соs0°=1, то tg 0°=0. Т.к. sin180°=0 и соs180°=1, то tg 180°=0
6 Котангенсом угла α называется отношение соsα к sinα, т.е.сtgα=соsα :sinα. При α=0° сtgα не определён, т.к. sin0°=0. При α=180° сtgα не определён, т.к. sin180°=0.
7 3.Основное тригонометрическое тождество Единичная полуокружность АСВ с центром О является дугой окружности, уравнение которой имеет вид х²+у²=1. Выполним 1012 (для точек М и М). Т.к. sinα=у, соsα=х, то sin ² α+ соs ² α=1. Данное равенство выполняется для любого α, 0°α180°. sin ² α+ соs ² α=1 – основное тригонометрическое тождество Выполним 1013а, 1014а, 1015а.
9 Построение угла, если известно значение тригонометрической функции этого угла. 1.Построим угол α, если sin α =0,25. Построение: 1)В системе координат Оху построим единичную полуокружность с центром в начале координат. 2)Проведём прямую у=0,25. 3)Прямая пересекла полуокружность в точках М и Р. 4)Проведём лучи ОР и ОМ. Углы АОР и АОМ – искомые. Задача имеет два решения. у у МР ОАх
10 2.Построим угол α, если соs α =0,25. Построение: 1)В системе координат Оху построим единичную полуокружность с центром в начале координат. 2)Проведём прямую х=0,25. 3)Прямая пересекла в точке М полуокружность. 4)Проведём луч ОМ. Угол АОМ – искомый. Задача имеет одно решение. уМ ОАх
11 2.Построим угол α, если соs α =-0,5. Построение: 1)В системе координат Оху построим единичную полуокружность с центром в начале координат. 2)Проведём прямую х=-0,5. 3)Прямая пересекла в точке М полуокружность. 4)Проведём луч ОМ. Угол АОМ – искомый. Задача имеет одно решение. у М ОАх
13 Самостоятельная работа 1 вариант2 вариант Постройте угол А, если 1) sinА=3/51) sinА=2/5 2) соsА=3/42) соsА=-3/4 3) соsА=-2/33) соsА=2/3 1018(а)1018(б) Домашнее задание §1, п.95, 1017, 1018(в), 1019(б)