Как построить спектр в матлабе
Спектральный анализ в пакете программ MATLAB
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Томский политехнический университет
«_____» ____________ 2010 г.
СПЕКТРАЛЬНЫЙ АНАЛИЗ В ПАКЕТЕ ПРОГРАММ MATLAB
по курсу “Цифровая обработка сигналов”
Лабораторная работа №4
Спектральный анализ в пакете программ MATLAB
1.1. изучение функций MATLAB Simulink для анализа спектра сигналов;
1.2. исследование преобразования спектра сигналов при прохождении через аналоговые фильтры.
2. КРАТКИЕ ПОЯСНЕНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ
2.1. Анализ спектра сигналов методом ДПФ (БПФ)
2.1.1. Дискретное преобразование Фурье
Дискретное преобразование Фурье (ДПФ), иллюстрируемое рис. 1, соответствует выборкам непрерывного преобразования Фурье (или спектра) 
где ∆ω=ωд/N – шаг дискретизации по частоте; N – число вычисляемых частотных выборок ДПФ в полосе частот <0 − ωд>, в общем случае не равное N1; k = 0, 1. N–1 – номер частотной выборки.
Рис. 1. Дискретизация сигнала в частотной области
Выбор шага дискретизации по частоте определяется возможностью восстановления сигнала x(n) и его непрерывного спектра 
Восстановление сигнала по дискретизированному по частоте спектру осуществляется с помощью обратного ДПФ (ОДПФ):
Преобразования ДПФ − ОДПФ (1), (2) представляют как в виде функции дискретной частоты ωk, так и номера частотной выборки k:


Вычисление ОДПФ и ДПФ требует N2 операций умножения и N×(N−1) операций сложения комплексных чисел.
Оба преобразования используют единый вычислительный алгоритм, основанный на их достаточно простой взаимосвязи:

где * − операция комплексного сопряжения.
При N ≥ N1 xp(n) = x(n), n = 0, 1.. N – 1, т. е. сигнал xp(n) на интервале 0…N–1 точно совпадает с исходным сигналом x(n), дополненным (N – N1) нулевыми отсчетами и является периодическим его продолжением за пределами этого интервала (рис. 2). ОДПФ, вычисляемое на интервале 0…N–1, обеспечивает в данном случае точное восстановление сигнала x(n) по его ДПФ.
При N ωд /N1) имеет место перекрытие периодизированных с периодом N последовательностей x(n) (явление наложения во временной области), так что xp(n) ≠ x(n) при n = 0.. N1−1 (рис. 3). Это исключает возможность точного восстановления сигнала по его дискретизированному спектру.
Рис. 2. Сигнал, соответствующий ОДПФ при N ≥ N1
Как правильно построить спектр сигнала
Здравствуйте! Вопрос прост, но в тоже время плаваю в нём. Имеется сигнал с фазовой манипуляцией, период сигнала и частота несущей. Необходимо построить спектр сигнала. Если известна его несущая частота 3 ГГц и длительность сигнала 30 мкс.
За основу получения сигнала с фазовой манипуляцией воспользовался этой темой: Формирование Фмн сигнала,выручайте
Построения выполнял следующим образом:
Построить амплитудный спектр сигнала
Доброго времени суток товарищи форумчане.Сейчас крайняя сессия перед дипломом(заочная форма.
Построить спектр сигнала одиночного радиоимпульса
Здравствуйте, как построить спектр сигнала одиночного радиоимпульса. помогите плиз
Построить спектр сигнала, разложив в ряд Фурье
Салют! Друзья, помогите найти ошибку. Имеем ЛЧМ сигнал, нужно разложить его в ряд Фурье и.
Как получить спектр сигнала?
Здравствуйте! Очень нужна помощь. Пытался: снять значение яркости каждого пикселя исходного.
Решение
То есть чем больше точек на дискретизацию я возьму, тем меньше по амплитуде получается спектр? Или я что-то не так понял? В обоих случаях я делю на количество точек дискретизации по частоте.
Видимо, я не корректно выбираю шаг дискретизации по частоте.
Constanti, Если следовать хелпу https://www.mathworks.com/help/matlab/ref/fft.html, то нормирование следует осуществлять делением на количество отсчетов сигнала, а не на длину преобразования Фурье.
Попробуйте делать так
Добавлено через 12 минут
Хотя, нет. Это я погорячился. Нормируют именно на параметр n функции fft.

Здравствуйте! Помогите, пожалуйста, построить спектр сигнала. Имеются записанные данные в виде.
Спектр сигнала
Здравствуйте, построил спектр сигнала по Фурье. Подскажите, что можно определить из данного графика?
Спектр сигнала
Уважаемые форумчане, доброго времени суток! Имеется два кода. Первый очень понятен, я понимаю.
Спектр сигнала
Написал программу, рассчитывающую спектр сигнала: f=50; t=0:1/1024:0.1; y=sin(2*pi*f*t);.
Документация
Быстрое преобразование Фурье
Синтаксис
Описание
Y = fft( X ) вычисляет дискретное преобразование Фурье (ДПФ) X использование алгоритма быстрого преобразования Фурье (FFT).
Если X вектор, затем fft(X) возвращает преобразование Фурье вектора.
Если X матрица, затем fft(X) обрабатывает столбцы X как векторы и возвращает преобразование Фурье каждого столбца.
Если X многомерный массив, затем fft(X) обрабатывает значения вдоль первого измерения массива, размер которого не равняется 1 как векторы и возвращает преобразование Фурье каждого вектора.
Если X матрица, затем каждый столбец обработан как в векторном случае.
Если X многомерный массив, затем первое измерение массива, размер которого не равняется 1, обработано как в векторном случае.
Примеры
Сигнал с шумом
Использование преобразования Фурье, для нахождения частотных составляющих сигнала, содержащего шум.
Задайте параметры сигнала с частотой дискретизации 1 кГц и длительностью сигнала 1,5 секунд.
Сформируйте сигнал, содержащий синусоиду на 50 Гц амплитуды 0.7 и синусоиду на 120 Гц амплитуды 1.
Повредите сигнал с нулевым средним белым шумом с отклонением 4.
Вычислите преобразование Фурье сигнала.
Теперь возьмите преобразование Фурье исходного, неповрежденного сигнала и получите точные амплитуды, 0.7 и 1.0.
Гауссов импульс
Преобразуйте Гауссов импульс от временного интервала до частотного диапазона.
Постройте импульс во временном интервале.
Преобразуйте Гауссов импульс в частотный диапазон.
Задайте частотный диапазон и постройте уникальные частоты.
Волны косинуса
Сравните волны косинуса во временном интервале и частотном диапазоне.
Задайте параметры сигнала с частотой дискретизации 1 кГц и длительностью сигнала 1 секунды.
Постройте первые 100 записей из каждой строки X на одной фигуре в порядке и сравнивают их частоты.
В целях эффективности алгоритма, fft позволяет вам заполнять вход конечными нулями. В этом случае заполните каждую строку X с нулями так, чтобы длина каждой строки была следующей более высокой степенью 2 от текущей длины. Задайте новую длину с помощью nextpow2 функция.
Вычислите преобразование Фурье сигналов.
Вычислите двусторонний спектр и односторонний спектр каждого сигнала.
В частотном диапазоне постройте односторонний амплитудный спектр для каждой строки на одной фигуре.
Входные параметры
X — Входной массив
вектор | матрица | многомерный массив
Входной массив, заданный как векторный, матричный или многомерный массив.
Если X пустая матрица 0 на 0, затем fft(X) возвращает пустую матрицу 0 на 0.
Типы данных: double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical
Поддержка комплексного числа: Да
n — Преобразуйте длину
[] (значение по умолчанию) | неотрицательный целочисленный скаляр
Пример: n = 2^nextpow2(size(X,1))
Типы данных: double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical
dim — Размерность, которая задает направление расчета
положительный целочисленный скаляр
Величина для работы, заданная как положительный целый скаляр. Если значение не задано, то по умолчанию это первый размер массива, не равный 1.
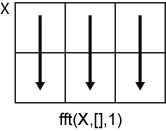
fft(X,[],1) действует вдоль столбцов X и возвращает преобразование Фурье каждого столбца.
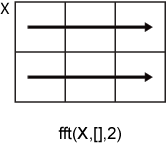
fft(X,[],2) действует вдоль строк X и возвращает преобразование Фурье каждой строки.
Типы данных: double | single | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical
Выходные аргументы
Y — Представление частотного диапазона
вектор | матрица | многомерный массив
Представление частотного диапазона, возвращенное как вектор, матрица или многомерный массив.
Размер Y следующие:
Типы данных: double | single
Больше о
Дискретное преобразование Фурье вектора
W n = e ( − 2 π i ) / n
один из корней из единицы n.
Советы
Время выполнения для fft зависит от длины преобразования. Преобразуйте длины, которые имеют только малые простые множители, значительно быстрее, чем те, которые являются главными или имеют большие простые множители.
Алгоритмы
Ссылки
[2] Frigo, M. и С. Г. Джонсон. fftw: Адаптивная Программная архитектура для БПФ”. Продолжения Международной конференции по вопросам Акустики, Речи и Обработки сигналов. Издание 3, 1998, стр 1381-1384.
Расширенные возможности
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Указания и ограничения по применению:
Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.
Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
Выход Y является всегда комплексным, даже если все мнимые части являются нулем.
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
Для распределенных массивов, вместо того, чтобы использовать параллельный Алгоритм бпф, fft собирает векторы на одном рабочем, чтобы выполнить главные БПФ длины. Для больших БПФ вектора главной длины могут закончиться ошибки из памяти.
Спектральный анализ осциллограмм в MATLAB
С полученными от осциллографа данными можно выполнять любые операции, которые предусмотрены в системе MATLAB и в десятках пакетов расширения этой мощной системы компьютерной математики. Покажем это на весьма важных примерах проведения спектрального анализа полученной осциллограммы различными методами, которые не реализованы в самом приборе и позволяют расширить его возможности.
К примеру, осциллографы TDS1000B/2000B не предусматривают возможность проведения спектрального анализа в линейном масштабе (задан только логарифмический). Ниже представлена программа (М-файл) spec_l, выполняющая вычисление и построение графика спектра с линейным масштабом для сигнала, отсчеты которого хранятся в векторе ydata:
%Вычисление и построение спектра в линейном масштабе Y = fft(ydata,NFFT)/L; %3адание БПФ
f = Fs/2.*linspace(0,1,NFFT/2); ^Создание вектора
plot(f,2*abs(Y(1:NFFT/2))) Построение графика
title(‘Single-Sided Amplitude Spectrum of y(t)’) xlabel(‘Frequency (Hz ) ‘ ) ylabel(‘Y(f)I’)
Для проведения спектрального анализа сигнала, осциллограмма которого имеется на экране осциллографа, необходимо вначале выполнить команду OSC (данные от осциллографа вводятся в MATLAB) и, после просмотра графика сигнала, команду scec_l. График будет заменен спектрограммой.
На рис. 4.53 показан пример импорта осциллограммы прямоугольного импульса — сигнала от генератора AFG3101 корпорации Teknronix. Масштаб по горизонтали выбран так, чтобы с одной стороны было представлено большое число периодов сигнала, а с другой стороны была видна форма импульсов.
На рис. 4.54 показан спектр прямоугольных импульсов с коэффициентом заполнения 10% и амплитудой 1 В. Он четко представляет гармоники спектра. В частности, отчетливо видно, что спектр имеет только нечетные гармоники, амплитуда которых убывает как 1 /к, где к — номер гармоники. Это полностью соответствует теоретическим представлениям о спектре меандра. Спектр характеризуется очень малым уровнем шума.
Рис. 4.53. Пример импорта прямоугольного импульса и построения его графика
На рис. 4.55 показана осциллограмма синусоидального сигнала с частотой 1 МГц, засоренная шумом (сигнал получен также от генератора AFG3101). Масштаб по горизонтали выбран так, что осциллограмма выглядит просто как шумовая дорожка — никаких признаков наличия синусоидального сигнала не наблюдается.
На рис. 4.56 показан спектр сигнала, изображенного на рис. 4.55. Весьма отчетливо видна единственная спектральная линия с пиком на частоте 1 МГц. Таким образом, в данном случае отчетливо выделен сигнал синусоидальной формы. О его синусоидальности говорит практически полное отсутствие других гармоник.
После того как данные сигнала осциллографа помещены в рабочее пространство (память) системы MATLAB командой OSC, над ними можно проводить операции как с помощью программных модулей (см. примеры выше), так и командами, вводимыми в командном окне. Например, следующие команды обеспечивают получение спектрограммы (периодограммы) с окном Блэкмана-Харриса:
Рис. 4.54. Спектр прямоугольного импульса (рис. 6.44)
Рис. 4.55. Осциллограмма зашумленной синусоиды при большой длительности развертки
Рис. 4.56. Спектр сигнала, показанного на рис. 4.55
Для прямоугольного импульса с частотой 1 МГц и коэффициентом заполнения 5% периодограмма показана на рис. 4.57. В данном случае вычисляется спектр мощности сигнала в логарифмическом масштабе, что дает очень широкий динамический диапазон периодограммы, в который входят и шумовые компоненты. Окно Блэкмана-Хар- риса эффективно выделяет гармоники спектра и подавляет шумовые компоненты. Уровень собственных боковых лепестков у этого окна ослаблен более чем на 100 дБ.
Источник: Дьяконов В. П. Генерация и генераторы сигналов / В. П. Дьяконов. — М. : ДМК Пресс, 2009. — 384 е., ил.
Построение спектрограмм осциллограмм в MATLAB
К сожалению, временное положение компонент сигнала обычный спектральный Фурье-анализ не выявляет. Для наглядной иллюстрации этого зададим (с помощью генератора AFG3101) сигнал в виде пачки из 10 периодов синусоидального зашумленного сигнала. После исполнения команды OSC получим данные осциллограммы в рабочем пространстве MATLAB. Для получения осциллограммы и спектра в данном случае воспользуемся мощным средством пакета расширения Signal Processing Toolbox — инструментом анализа сигналов, фильтров и спектров SPTool. Запустив его командой sptool, можно из его окна загрузить массив ydata и наблюдать как сам сигнал, так и его спектр (см. рис. 4.58) при разных установках и разных видах спектрального анализа.
Рис. 4.57. MATLAB-периодограмма прямоугольного импульса
Рис. 4.58. Пример просмотра радиоимпульса и построения его спектра
Высокая спектральная линия на спектрограмме отчетливо видна и говорит о наличии синусоидального сигнала с частотой 1 МГц. Однако о местоположении сигнала во времени и о его длительности спектрограмма не дает никаких намеков, хотя в этом средстве можно проводить спектральный анализ многими методами.
Функция specgram обеспечивает выполнение скользящего оконного БПФм построение спектрограммы в плоскости частота-время с разбивкой времени на ряд участков, размер которой задается размером скользящего окна и длительностью сигнала. Интенсивность спектральных составляющих определяется цветом прямоугольников, из которых состоит спектрограмма. Например, для сигнала на рис. 4.58, выполнение команды
создает спектрограмму, показанную на рис. 4.59. На ней среди шумовых компонент (хаотично разбросанные прямоугольники разного цвета) отчетливо выделяется область времени, в которой расположена компонента сигнала в виде пачки синусоид. Хорошо видно, что эта область занимает отрезок времени от 7,5 до 17,5 мкс, т. е. местоположение основной компоненты сигнала и ее длительность четко определяются и совпадают с положением пачки синусоид на рис. 4.59. В указанной области снизу отчетливо видна сплошная темно-коричневая линия синусоидальной составляющей с частотой 1 МГц. На синусоидальность ее указывает отсутствие высших гармоник.
Рис. 4.59. Спектрограмма радиоимпульса
Поскольку ширина данной области равна 10 мкс, то из спектрограммы ясно, что компонента сигнала является пачкой из 10 синусоид! Спектрограммы со скользящим временным окном, таким образом, отчетливо выделяют особенности сигнала во временной области и позволяют оценивать параметры сигнала (начало появление его компонент, их длительность, временное положение), которые невозможно оценить обычным преобразованием Фурье. В некоторых случаях, как в приведенном примере, возможно даже выявление формы сигнала.
Приведенные примеры из области спектрального анализа демонстрируют лишь малую часть весьма обширных средств системы MATLAB, расширяющих возможности осциллографов. Так, для проведения спектрального анализа MATLAB имеет целый ряд функций, например оконного спектрального анализа с почти 20 видами окон. Для сравнения отметим, что спектральный анализ с помощью осциллографов TDS1000В/ 2000В возможен только при трех окнах. Есть даже функции спектрального анализа на основе новейших вейвлет-преобразований [5] и проектирования фильтров. Возможности математической обработки сигналов и осциллограмм практически не ограничены.
Впрочем, нельзя не отметить и серьезное ограничение описанного подхода — обрабатываются только отдельные фрагменты сигналов, которые задаются осциллограммой, представляющей сигнал в определенном промежутке времени. Это значит, что работа в реальном масштабе времени не обеспечивается.
В последнее время большой интерес представляет вейвлет-анализ и синтез сигналов по новому математическому базису вейвлетов (коротких «волночек»). Он пригоден для нестационарных сигналов. Однако рассмотрение теории и практики применения вейвлет-анализа и синтеза сигналов далеко выходит за рамки тематики данной книги. Заинтересованный читатель может ознакомиться с ним в книге автора [108]. В ней впервые описаны пакеты расширения по вейвлетам систем компьютерной математики Mathcad, Mathematica и MATLAB.
Источник: Дьяконов В. П. Генерация и генераторы сигналов / В. П. Дьяконов. — М. : ДМК Пресс, 2009. — 384 е., ил.