Как построить равносторонний треугольник без циркуля
Как начертить равносторонний треугольник
Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.
На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.
Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.
При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.
Отметьте точки пересечения окружностей.
Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.
Далее, через центры обеих окружностей нужно провести прямую линию.
Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.
Соедините все три точки между собой.
Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.
Как построить высоту треугольника — основные способы
Для решения многих геометрических задач учащемуся нужно уметь быстро построить высоту треугольника. Сделать это можно несколькими простыми для восприятия способами, которые подходят для фигуры разной формы и размера. Весь процесс состоит из определённой последовательности действий, правильно выполнить которые сможет каждый школьник.
С применением циркуля
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.
Способ начертить искомый отрезок:
Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.
С помощью линейки
Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.
В остроугольном треугольнике
Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.
Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.
Правильная последовательность действий:
В тупоугольной фигуре
Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.
Порядок действий:
В прямоугольном и равнобедренном
В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.
Пошаговая инструкция:
Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.
Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:
Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.
Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.
Построение при помощи циркуля и линейки, только… без циркуля
Все мы знакомы из школьной программы с построениями при помощи циркуля и линейки. А что будет, если вдруг циркуль затеряется? Можно ли при помощи одной линейки строить ещё что-то нетривиальное? Предлагаю вашему вниманию задачу, решение которой принесло мне немало приятных часов. Задача со звёздочкой, поэтому не расстраивайтесь, если сходу решение не найдёте. Хотя один мой знакомый справился за пять минут, думаю, что это скорее исключение из правил.
Итак, на плоскости есть отрезок, который мы бы хотели продолжить. Казалось бы, выбрать две точки на отрезке, приложить линейку и прочертить прямую. Но вот незадача: как раз на пути этой прямой посажено жирное пятно кетчупа, а мы линейку пачкать не хотим. Нужно продолжить изначальную прямую за пятном, не прикасаясь к нему линейкой.
Напоминаю, циркуля нет, остаётся только неградуированная линейка, с помощью которой можно только проводить прямую через выбранные две точки, больше ничего. Это настоящая задача без подколок. Складывать листочки, использовать вторую сторону линейки для откладывания параллельных линий, а также хитрить другими подобными способами не требуется.
Update: Поскольку в комментариях задачу расщёлкали как орех, публикую два моих решения. Подглядывать в ответы, не попытавшись решить задачу самостоятельно, неспортивно 🙂
Отвлечёмся для начала от кетчупа, и попробуем нарисовать просто тетраэдр с основанием ABC и вершиной S. А затем проведём плоскость, порождённую треугольником A’B’C’, пересекающую рёбра тетраэдра:
Прямые AB и A’B’ пересекаются в точке P1, поскольку лежат в одной и той же плоскости (грань тетраэдра ABS). Аналогично P2 — точка пересечения прямых BC и B’C’, и P3 — пересечение прямых AC и A’C’.
При этом P1, P2 и P3 лежат на одной прямой, поскольку принадлежат одновременно плоскости ABC и плоскости A’B’C’, а пересечение двух плоскостей — это прямая.
То есть, произвольно взяв две точки P1 и P2 на нашем отрезке, мы можем построить P3, лежащую на той же прямой, но с другой стороны пятна. Повторив построение ещё раз, получим вторую точку, и задача решена. На всякий случай, это применение теоремы Дезарга
Лично я про проективную геометрию даже и не думал, и честно рисовал эти самые тетраэдры. Мой коллега (который решил за пять минут) предложил элегантное решение, основанное на теореме Паппа. Это решение должно быть очевидно всем, кто занимался компьютерной графикой.
Наша прямая — синяя, эллипс — пятно кетчупа. Основная идея — нарисовать проекцию 3д плоскости, замощённой одинаковыми квадратиками кафеля. Точки A и B — это так называемые точки схода, то есть, точки, в которых пересекаются параллельные (в 3д) прямые, образующие границы кафельных плиток.
1. Проведём две произвольных фиолетовых прямых таким образом, чтобы точка их пересечения лежала на нашей синей прямой.
2. Выберем произвольную точку A на нашей синей прямой, и произвольно же проведём две голубых прямых.
3. Пересечение фиолетовых и голубых прямых даст четыре точки P, Q, R и S, которые являются углами главной кафельной плитки, от которой мы и будем плясать.
4. Нарисуем красные прямые QP и RS, и обозначим точку их пересечения как B, это будет вторая точка схода.
5. Ну а дальше дело техники: произвольно чертим три розовые прямые, получим ещё две плитки кафеля. Ищем их центры, начертив два жёлтых креста, и дело сделано.
Узнать ещё
Знание — сила. Познавательная информация
Как нарисовать равносторонний треугольник
Как нарисовать равносторонний треугольник, используя только линейку и карандаш? Этот способ позволяет быстро сделать рисунок правильного или равнобедренного треугольника.
Как нарисовать равнобедренный треугольник
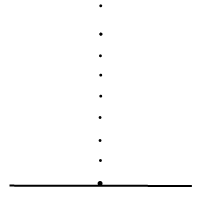
Рисунок начинаем с основания. Длину основания подбираем такой, чтобы ее удобно было делить пополам (берем четное количество клеточек). Вершину треугольника отмечаем ровно над серединой основания:
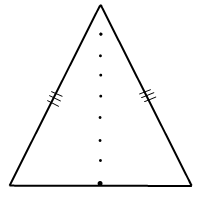
Если нужен равнобедренный треугольник, у которого боковая сторона больше основания, вершину ставим повыше:
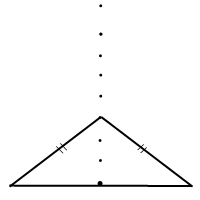
Если требуется треугольник, основание которого больше боковой стороны, то вершину отмечаем ниже:
Как нарисовать равносторонний треугольник
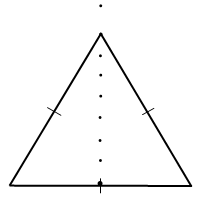
От конца основания откладываем отрезок равной ему длины так, чтобы второй конец этого отрезка расположился ровно над серединой основания. Соединяем вершину треугольника с другим концом основания:
Если в задаче о равнобедренном треугольнике речь идет о высоте, биссектрисе и медиане, проведенным к основанию, достаточно соединить вершину треугольника с отмеченной серединой основания:
Построение с помощью циркуля и линейки — описание, алгоритмы и задачи
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
Построение отрезка, равного данному
Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Построение угла, равного данному
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Построение правильного четырехугольника вписанного в окружность
Вариант 1
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Построение вписанного в окружность правильного пятиугольника
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.