Как построить прямую пересечения плоскостей
Построение линии пересечения плоскостей, заданных различными способами
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L1 и L2, принадлежащих линии пересечения.
Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.
Пересечение плоскостей, заданных следами
Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П1 и П2.
Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.
Пересечение плоскостей треугольников
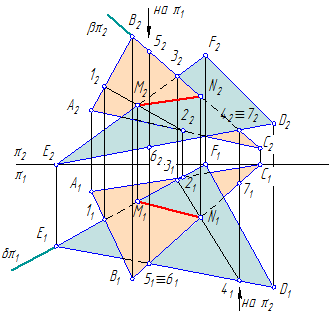
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.
Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.
Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π2. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π2. С противоположной стороны от линии N»K» видимость треугольников меняется.
Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π1. Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Задание 2. Построение линии пересечения плоскостей
2.1. Условие задания
По заданным координатам точек А, В, С, D, E, F (Таблица 2) построить горизонтальную и фронтальную проекции треугольников ∆АBC и ∆DEF, найти линию их пересечения и определить видимость элементов треугольников.
2.2. Пример выполнения задания № 2
Второе задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам шести точек А, В, С, D, E, Fпостроить горизонтальную и фронтальную проекции 2-х плоскостей, заданных ∆АBC и ∆DEF;
2. Плоскости общего и частного положения, пересечение прямой и плоскости, пересечение плоскостей, конкурирующие точки: построить линию пересечения заданных плоскостей и определить видимость их элементов.
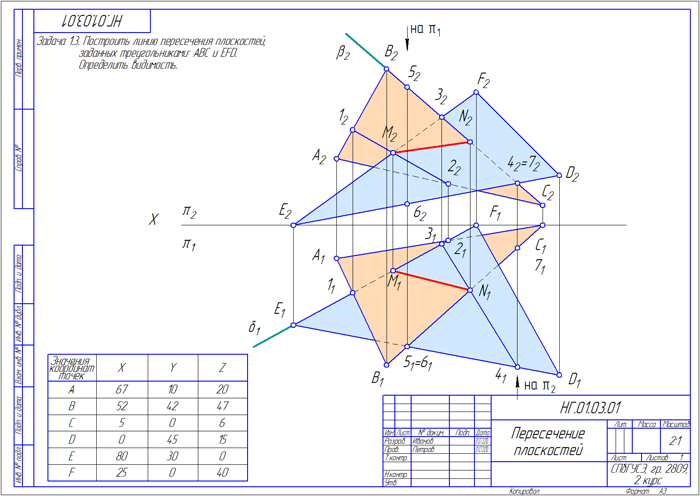
Построить горизонтальные и фронтальные проекции заданных плоскостей ∆АBC и ∆DEF (Рисунок 2.1).
Для построения искомой линии пересечения заданных плоскостей необходимо:
1. Выбрать одну из сторон треугольника и построить точку пересечения этой стороны с плоскостью другого треугольника: на Рисунке 2.1 построена точка М пересечения прямой EF c плоскостью ∆АBC; для этого прямую EF заключают во вспомогательную горизонтально-проецирующую плоскость δ;
2. Построить фронтальную проекцию 1222 линии пересечения плоскости δ с плоскостью ∆АBC;
3. Найти фронтальную проекцию М2 искомой точки М на пересечении фронтальную проекцию 1222 с фронтальной проекцией E2 F2прямой EF;
4. Найти горизонтальную проекцию М1 точки М с помощью линии проекционной связи;
5. Аналогично построить вторую точку N, принадлежащую искомой линии пересечения заданных плоскостей: заключить во фронтально-проецирующую плоскость β прямую ВС; найти линию пересечения 34 плоскости с плоскостью ∆DEF; на пересечении линии 34 и прямой ВС найти точку N;
6. Определить с помощью конкурирующих точек, для каждой плоскости отдельно, видимые участки треугольников.
Рисунок 2.1 – Построение линии пересечения двух плоскостей, заданных треугольниками
Рисунок 2.2 – Пример оформления задания 2
Как построить прямую пересечения плоскостей

Построение линии пересечения двух плоскостей.
Одной из основополагающих задач начертательной геометрии является задача на на построение линии пересечения двух плоскостей общего положения. Случаи задания плоскостей бывают разные, но в любом случае вам встретится задача, в которой будет необходимо построить линию пересечения двух плоскостей заданных треугольниками (или другими плоскими геометрическими фигурами). Алгоритм решения такой задачи я и предлагаю рассмотреть сейчас.
(Если же ваши плоскости заданы не треугольниками, а, например, параллельными прямыми, то приглашаю вас прочитать еще один урок, посвященный тому, как найти линию пересечения двух плоскостей.)
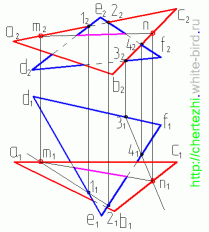
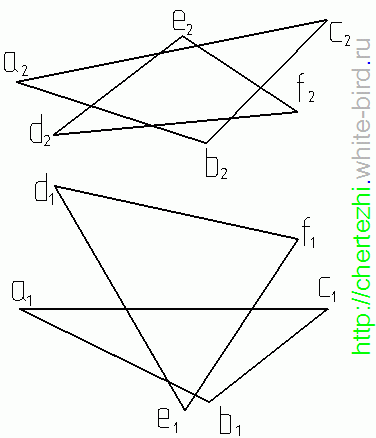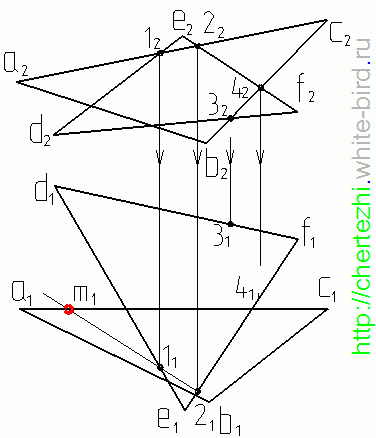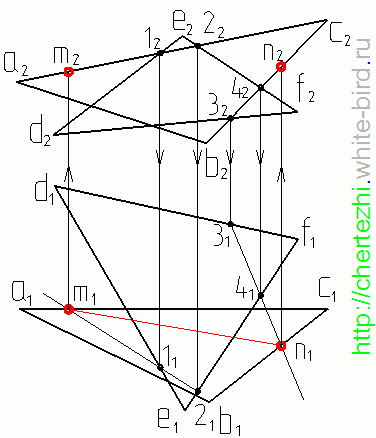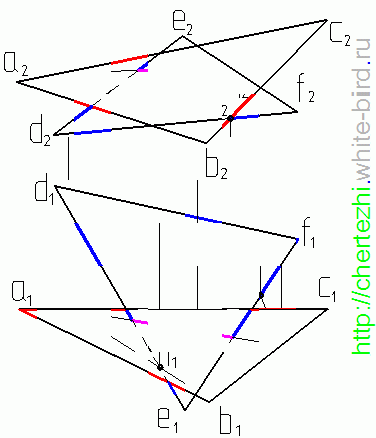
Итак, даны две плоскости, заданные треугольниками АВС и DEF. Метод сводится к тому, что бы поочередно найти две точки пересечения двух ребер одного треугольника с плоскостью другого. Соединив эти точки мы получим линию пересечения двух плоскостей. Построение точки пересечения прямой с плоскостью более подробно было рассмотрено в предыдущем уроке, напомню только механические действия:
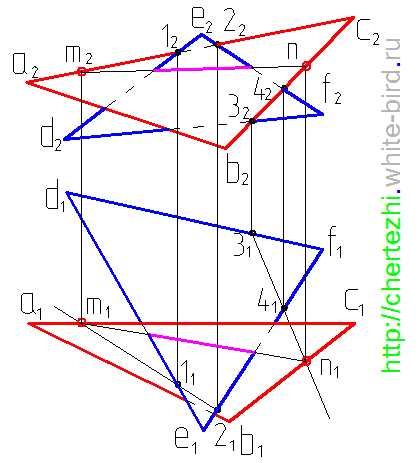
При помощи наиболее внимательных посетителей сайта удалось найти неточность при определении видимости плоскостей. Ниже приведен чертеж, на котором исправлена видимость линий, ограничивающих плоскости на горизонтальной плоскости проекций:
Вы можете сказать «спасибо!» автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»
Автор комментария: Сир_Иван
Дата: 2010-12-19
а я понять не мог никак, спасибо.
Автор комментария: надежда
Дата: 2011-12-13
Автор комментария: Дебердеева
Дата: 2012-01-20
Автор комментария: макс
Дата: 2012-01-23
Автор комментария: Леха
Дата: 2012-03-20
Автор комментария: степан
Дата: 2012-03-30
Автор комментария: Хадыжа
Дата: 2012-03-31
Автор комментария: Саня
Дата: 2012-10-02
Большое спасибо, очень доходчиво написано!
Автор комментария: Алька
Дата: 2012-10-07
Автор комментария: инна
Дата: 2012-10-12
ААААААААААААААААААААААААА. вы спасли меня.
Автор комментария: Степан
Дата: 2012-10-13
Автор комментария: Сан
Дата: 2012-10-17
Автор комментария: Владислав
Дата: 2012-11-05
Вот спасибо, товарищи!)) Отличная статья!
Автор комментария: Всеволод
Дата: 2012-11-07
Хух спасибо выручили и руп в ближайшее время кину
Автор комментария: Дмитрий
Дата: 2012-11-10
Неправильно определена видимость треугольников в плоскости XY. Легко проверить методом конкурирующих точек. [URL=http://www.radikal.ru][IMG]http://s017.radikal.ru/i401/1211/50/b3aba0648f63.jpg[/IMG][/URL]
Автор комментария: Дмитрий
Дата: 2012-11-10
Хотел вставить картинку с пояснениями, а тут тег [IMG] [/IMG] не работает. Пояснения здесь http://s017.radikal.ru/i401/1211/50/b3aba0648f63.jpg
Автор комментария: Александр
Дата: 2012-11-12
To Дмитрий: Согласен, что ошибка в видимости, но только не в XY, а в XZ. Сделал подобный чертез в простеньком 3D редакторе: http://s59.radikal.ru/i163/1211/8b/bc5f07b225d9.jpg Так должно быть. =)
Автор комментария: Александр
Дата: 2012-11-12
Автор комментария: Дмитрий
Дата: 2012-11-12
Александр, возможно, я ошибся. Но давайте проверим видимость в плоскости XZ с помощью конкурирующих точек. В моем примере это G и H см. рис. http://s47.radikal.ru/i118/1211/b9/d29b24b27c65.jpg Кажется все правильно. Поправьте меня если это не так.
Автор комментария: Александр
Дата: 2012-11-12
Да, Дмитрий, сейчас немного подумал и понял, что просто перепутал фронтальный и горизонтальный виды, поэтому все с точьностью наоборот получилось. Вы правы. =)
Автор комментария: Черт
Дата: 2012-11-14
Бред.
Да, согласен. Бред. Так говорят все, это нормально. См. рубрику Юмор
Автор комментария: рома
Дата: 2012-12-07
спасибо большое! мне эта стаття очень помогла. очень доходчиво был показан алгоритм на анимации. спасибо, еще раз:)))
Автор комментария: Антон
Дата: 2012-12-08
А если у меня не получается одна из точек,т.е точка м не лежит на ас,что делать?
Антон, доброго дня. Если вы имеете ввиду, что линия проведенная через 12 проходит мимо АС- просто продлите отрезок АС таким образом, чтоб все же найти точку пересечения этих ПРЯМЫХ. Их отрезки- лишь обозначенная их часть. Так что смелее. Это часто встречается.
Автор комментария: Людмила
Дата: 2012-12-13
Автор комментария: Арман
Дата: 2013-01-14
Автор комментария: Александр
Дата: 2013-01-24
Спасибо огромное! ГИФка просто супер, все понятно)
А ведь есть и те, кому не нравится 🙂 Но я не в силах отказаться от этого «спорта»! Жаль только, что никак не найду времени исправить ошибку.
Автор комментария: Варя
Дата: 2013-01-31
Огроменное Вам спасибо.
Автор комментария: Андрей
Дата: 2013-02-07
Автор комментария: игорь
Дата: 2013-04-18
мне нужно построить пересечение двух непрозрачных фигур треугольника ABC и параллелограмма DEFG. координаты а(185.140.115)b(0.30.45)c(105.0.15)d(165.115.0)e(215.55.30) f(65.25.115) вот вопрос почему один из треугольников не пересекается с параллелограммом и можно ли решить эту задачу!
Автор комментария: Юра
Дата: 2013-09-21
Автор комментария: Сергей
Дата: 2013-12-22
Автор комментария: бес
Дата: 2014-11-16
Автор комментария: Лера
Дата: 2015-10-17
Спасибо огромное! Мучаюсь уже около часа, методичка не помощник, а Ваша гифка все расставила на свои места!
Лера, вы молодец! А ведь что интересно: многие ругают мою псевдонимацию 🙂 Успехов вам!
Автор комментария: Иван
Дата: 2015-11-23
Полностью присоединяюсь к Лере) Ваша гафа просто четкая. Наглядно видно что да как делать. Все супер. Спасибо)
Автор комментария: гость
Дата: 2015-12-28
Автор комментария: Василий
Дата: 2016-10-13
Спасибо! Всё понятно. Чётко и без мути
Добавьте свой комментарий:
Наша страница в ВК:
Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
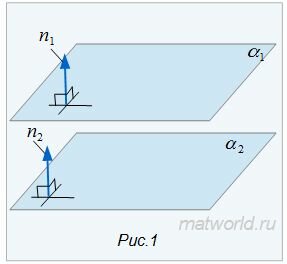 |
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
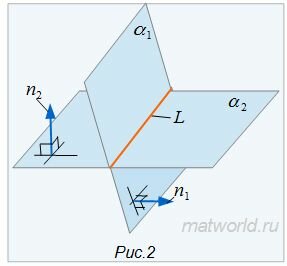 |
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=<A1, B1, C1> и n2=<A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
Равенство (5) можно записать в следующем виде:
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
Пример 1. Найти линию пересечения плоскостей α1 и α2:
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
где t− произвольное действительное число.
Запишем (11) в следующем виде:
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
Из равентсв выше получим каноническое уравнение прямой:
 |
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
 |
Пример 2. Найти линию пересечения плоскостей α1 и α2:
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Презентация по геометрии на тему «Построение точки пересечения прямой и плоскости и линии пересечения плоскостей»
Описание презентации по отдельным слайдам:
Математический диктант. Вариант 1. Вариант 2. 1. Назовите основные фигуры в пространстве. 2. Сформулируйте А2. 3. Сформулируйте А3. 4. Могут ли прямая и плоскость иметь две общие точки? 5. Сколько плоскостей можно провести через три точки? 1. Назовите основные фигуры на плоскости. 2. Сформулируйте аксиому А1. 3. Сколько плоскостей можно провести через прямую и не лежащую на ней точку? 4. Сколько может быть общих точек у прямой и плоскости? 5. Могут ли прямая и плоскость иметь только одну общую точку?
Проверка. Вариант 1. Вариант 2. 1. Точки, прямые и плоскости. 1. Точки, прямые и отрезки. 2.Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. 3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. 4. Могут. 5. если три точки лежат на одной прямой, то через них можно провести бесконечно много плоскостей; если три точки не лежат на одной прямой, то через них можно провести единственную плоскость 2.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 3. Одну 4. Если прямая пересекает плоскость, то одна; если лежит в плоскости, то бесконечно много; если параллельна плоскости, то ни одной; 5. Да
Чтобы построить точку пересечения прямой с данной плоскостью, нужно: Поместить прямую в плоскость. 2. Найти линию пересечения этой плоскости и данной. 3. Построить точку пресечения полученной прямой и данной.
Задача 2. Постройте точку пересечения прямой MN с плоскостью грани BCD тетраэдра ABCD, где M принадлежит AB, N принадлежит ADC. M N Построение: 1.Достроим AN до пересечения с CD, получим точку P. Р 2.Поместим MN в плоскость APB. 3.PB- линия пересечения плоскостей APB и BCD. 4.Достроим MN до пересечения с PB, полученная точка S –искомая точка пересечения прямой MN и плоскости BCD. S
Чтобы построить точку пересечения прямой с данной плоскостью, нужно: Поместить прямую в плоскость. 2. Построить (найти) линию пересечения этой плоскости и данной. 3. Построить точку пресечения полученной прямой и данной.
3. Достроим MN до пересечения с прямой PQ, получим точку S – точка пересечения прямой MN с плоскостью грани BCD. 2. Построим линию пересечения плоскостей APQ и BCD. Так как P и Q являются общими точками этих плоскостей, то проводя прямую через эти точки, получим линию пересечения плоскостей APQ и BCD. Задача 3. Постройте точку пересечения прямой MN с плоскостью грани BCD, где M принадлежит ABC, N принадлежит ADC. M N Построение: 1. Поместим прямую MN в плоскость, для этого достроим AM и AN до пересечения с рёбрами CB и DC. Получим точки Q и P. Р Q S
Чтобы построить линию пересечения двух плоскостей, нужно: 1. Выбрать в заданной плоскости 2 прямые. 2. Найти точки пересечения выбранных прямых с плоскостью, которую пересекает заданная плоскость. 3.Полученные точки задают прямую, которая является следом секущей плоскости.
М К N Р 2.4 Поместим прямую MN в плоскость, для этого достроим AN до пересечения с ВD, получим точку Q. Плоскость АQD- есть та плоскость, которой принадлежит MN. Q 2.5 Построим линию пересечения плоскостей АQC и BCD. Для этого необходимо найти две общие точки этих плоскостей. Так как точка C является вершиной тетраэдра, то она принадлежит АQC и BCD, так как точка Q принадлежит АQC и BCD (так как Q принадлежит DB, а DB лежит в BCD), то CQ–линия пересечения плоскостей АQC и BCD. 2.6 Построим точку пересечения прямой MN и CQ. S S –точка пересечения прямой MN и плоскости BCD. 3. PS- искомая линия пересечения плоскости заданной точками M, N и K и плоскости грани BCD тетраэдра ABCD.
Задача 6. Построить линию пересечения плоскостей заданной точками M, N и K и плоскостью грани BCD тетраэдра ABCD, где M принадлежит AB, N принадлежит ABC, K принадлежит ADC. M N K X Y P S
Чтобы построить точку пересечения прямой с данной плоскостью, нужно: Поместить прямую в плоскость. 2. Построить (найти) линию пересечения этой плоскости и данной. 3. Построить точку пресечения полученной прямой и данной.
Чтобы построить линию пересечения двух плоскостей, нужно: 1. Выбрать в заданной плоскости 2 прямые. 2. Найти точки пересечения выбранных прямых с плоскостью, которую пересекает заданная плоскость. 3.Полученные точки задают прямую, которая является следом секущей плоскости.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-674379
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Москве новогодние каникулы в школах могут начаться с 27 декабря
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Большинство родителей в России удовлетворены качеством образования в детсадах
Время чтения: 2 минуты
Петербургский Политех перевел студентов на дистанционку
Время чтения: 1 минута
НИУ ВШЭ откроет первую в России магистратуру по управлению низкоуглеродным развитием
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.