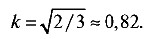Как построить призму в изометрии

Изометрическая проекция

В изометрической проекции все коэффициенты равны между собой:

Следовательно, при построении изометрической проекции размеры предмета, откладываемые по аксонометрическим осям, умножают на 0,82. Такой перерасчет размеров неудобен. Поэтому изометрическую проекцию для упрощения, как правило, выполняют без уменьшения размеров (искажения) по осям х, y, z, т.е. принимают приведенный коэффициент искажения равным единице. Получаемое при этом изображение предмета в изометрической проекции имеет несколько большие размеры, чем в действительности. Увеличение в этом случае составляет 22% (выражается числом 1,22 = 1 : 0,82).

Каждый отрезок, направленный по осям х, у, z или параллельно им, сохраняет свою величину.

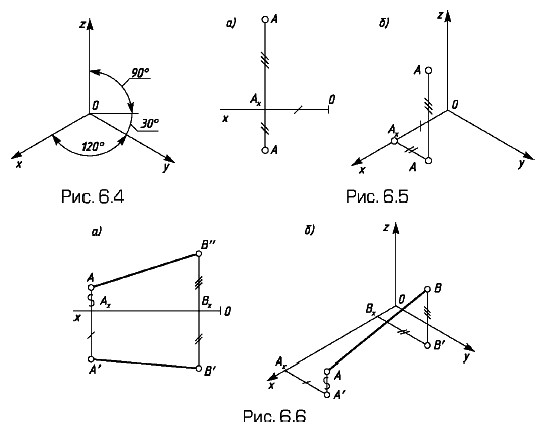
Расположение осей изометрической проекции показано на рис. 6.4. На рис. 6.5 и 6.6 показаны ортогональные (а) и изометрические (б) проекции точки A и отрезка АВ.

Шестигранная призма в изометрии

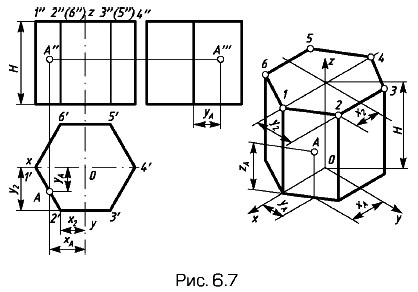
Построение шестигранной призмы по данному чертежу в системе ортогональных проекций (слева на рис. 6.7) приведено на рис. 6.7. На изометрической оси z откладывают высоту H, проводят линии, параллельные осям х и у. Отмечают на линии, параллельной оси х, положение точек 1 и 4.

Для построения точки 2 определяют координаты этой точки на чертеже — х₂ и у₂ и, откладывая эти координаты на аксонометрическом изображении, строят точку 2. Таким же образом строят точки 3, 5 и 6.

Построенные точки верхнего основания соединяют между собой, проводят ребро из точки 1 до пересечения с осью х, затем — ребра из точек 2, 3, 6. Ребра нижнего основания проводят параллельно ребрам верхнего. Построение точки А, расположенной на боковой грани, по координатам х_А (или у_А) и z_A очевидно из рис. 6.7.

Источник

Пример выполнения многоугольника (призмы) в изометрии

Построение многоугольника в изометрии

Построение окружности в диметрии

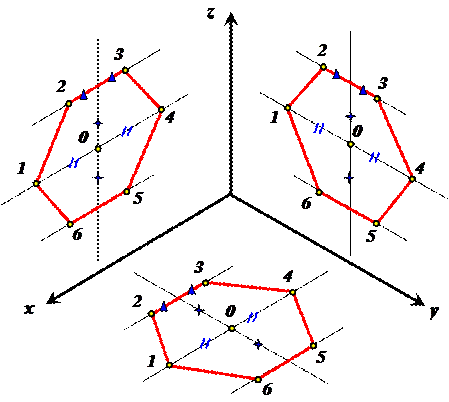Последовательность построения:

1. Построить оси диметрии;

2. Построить малую ось эллипса, параллельно отсутствующей оси;

3. Построить большую ось эллипса, перпендикулярно малой;

4. Провести исходную окружность (R=20);

Профильная и горизонтальная проекции:

6. Отметить точки 1, 2

7. Провести дугу окружности из центра О1 радиусом О1 1;

8. Провести дугу окружности из центра О2 радиусом О2 2;

9.Отметить точки О3, О4;

10. Провести дугу окружности из центра О3 радиусом О3 1;

11.Провести дугу окружности из центра О4 радиусом О4 2;

Фронтальная проекция:

12. Отметить точки 1,2 и провести через них горизонтальные линии;

14. Провести дуги окружностей радиусами О₁1, О₃2, О₂1, О₄2.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Комплексный чертеж призмы

Разделы: Технология

2.1. Многогранники
2.2. Сечение многогранников

2.3. Построение 6-угольной призмы с сечением фронтально-проецирующей плоскостью.
2.4. Построение развертки усеченной призмы.

Ход занятия

1. Вопросы для повторения:

Какие бывают прямые и плоскости?

— Общего и частного положения.

Как располагаются в пространстве проецирующие прямые и проецирующие плоскости?

— Они перпендикулярны плоскостям проекций.

Назовите способы преобразования чертежа.

— Способ вращения, способ перемены плоскостей проекций.

Когда применяется способ перемены плоскостей проекций?

— Когда требуется определить натуральную величину наклонного сечения для построения развертки геометрического тела.

2. Записываем новую тему “Многогранники”.

Форма многих технических деталей представляет собой сочетание простых геометрических тел. Поэтому для выполнения чертежей изделий необходимо знать, как правильно изображаются различные геометрические тела. Рассмотрим построение на комплексном чертеже основных геометрических тел: призмы, пирамиды, цилиндра, конуса, сферы, тора.

Призма.

Рассмотрим 3 проекции 6-угольной призмы. На главном виде – это прямоугольники, боковые ребра – это горизонтально проецирующие прямые, 6-угольник на виде сверху представляет собой проекцию обоих оснований.

Сечение призмы выполнено фронтально-проецирующей плоскостью.

Сечение поверхности геометрических тел плоскостью называется плоская фигура, точки которой принадлежат и поверхности тела, и секущей плоскости. Сечение широко применяется в техническом черчении для выявления формы и внутреннего устройства предметов. В сечении многогранника плоскостью образуется многоугольник. Вершины многоугольника – это точки пересечения ребер многогранника с секущей плоскостью, стороны – это линии пересечения секущей плоскости с гранями многогранника.

Рассмотрим все поставленные задачи.

Разверткой (выкройкой) поверхности тела называется плоская фигура, полученная путем совмещения всех точек данной поверхности с плоскостью без разрывов и складок.

Построение разверток выполняется обычно графическими приемами, с применением способов, предлагаемых начертательной геометрией. Построение развертки поверхности многогранника сводится к определению истинной величины каждой его грани по чертежу многогранника (см. Рис. 1). После этого грани многогранника стыкуются (соединяются) по ребрам и вершинам.

Для решения задачи 3 выполняем следующие операции:

Проводим горизонтальную прямую, на которой от произвольно выбранной точки А, откладываем отрезки AB, BC, CD, DE, EF, FA, равные длине стороны основания а = 30.

Из точек A, B, C, D, E, F, A восстанавливаем перпендикуляры и на них откладываем величины ребер усеченной призмы. Величины данных отрезков A1, B2, C3, D4, E5, F6, A1 берем с фронтальной проекции усеченной призмы. Полученные точки соединяем и получаем развертку боковой поверхности призмы.

К одному из отрезков основания, например к BC, пристраиваем 6-угольник ABCDEF.

К одному из звеньев ломаной, например, к отрезку 2-3, пристраиваем 6-угольник 123456 (сечение призмы), который переносим, используя метод засечек, с рисунка 1.

Рис 1

Строим усеченную 6-и угольную призму в изометрии. Сторона основания призмы, а = 30. Для выполнения задачи учащимся раздаются трафареты 6-и угольника в изометрии. Высоты A1, B2, C3, D4, E5, F6 – берем с фронтальной проекции усеченной призмы.

Источник

Урок 16. Построение аксонометрических проекций призмы, пирамиды

Графическая работа на компьютере №6
Лист 1. Тема урока Построение аксонометрических проекций призмы, пирамиды.
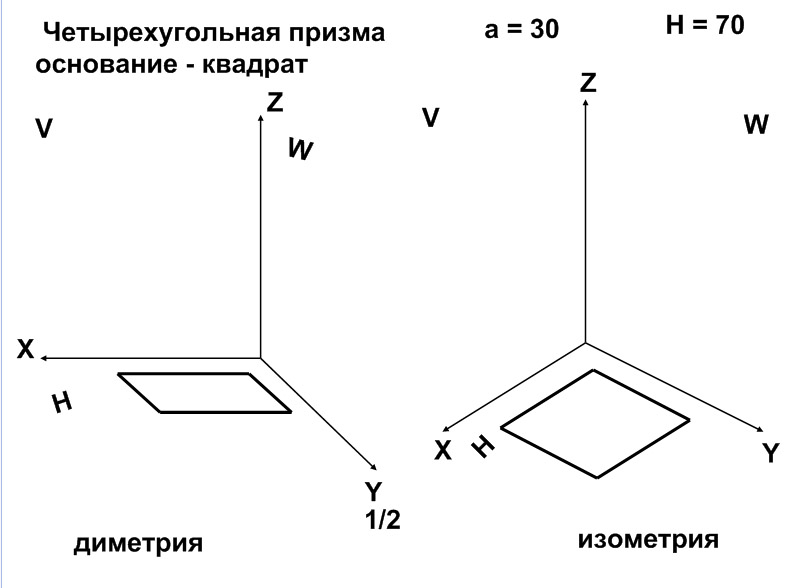
Лист 2. Построение четырехугольной призмы в основании квадрат (сторона квадрата = 30 мм, высота призмы = 70 мм).

Рис. 16.1 Рис. 16.2
Лист 3. Из каждой вершины основания восстанавливаем перпендикуляры (параллельные оси Z), равные высоте 70 мм (см. рис. 16.3).
Лист 4. Соединяем концы отрезков – получаем верхнее основание призмы.

Рис. 16.3 Рис. 16.4
Лист 5. Обводим толстой линией видимые контуры призмы (см. рис. 16.4).
Лист 6. Построение треугольной призмы, в основании равнобедренный треугольник с размерами: основание треугольника равна 30 мм, высота треугольника равна 35, высота призмы 70 мм. Откладываем размер высоты (35 мм) основания равнобедренного треугольника по оси Y (в диметрии в два раза меньше), по оси Х размер основания (30 мм) треугольника (см. рис. 16.5).

Рис. 16.5 Рис. 16.6
Лист 7. Построение основания треугольной призмы. Соединяем точки основания и высоты – получаем основание призмы (см. рис. 16.6).
Лист 8. Из вершин основания восстанавливаем перпендикуляры (параллельно оси Z), равные высоте призмы 70 мм (см. рис. 16.7).

Рис. 16.7 Рис.16.8
Лист 9. Соединяем концы отрезков – получаем верхнее основание призмы (см. рис. 16.8).
Лист 10. Обводим толстой линией видимые контуры призмы (см. рис. 16.9).

Рис. 16.9 Рис. 16.10
Лист 11. Построение шестиугольной призмы. Диаметр основания 40 мм, высота призмы 70 мм (см. рис. 16.10).
Лист 12. Из вершин основания восстанавливаем перпендикуляры (параллельно оси Z), равные высоте призмы 70 мм (см. рис. 16.11).

Рис. 16.11 Рис. 16.12
Лист 13. Соединяем концы отрезков – получаем верхнее основание призмы (см. рис. 16.12).
Лист 14. Обводим толстой линией видимые контуры призмы (см. рис. 16. 13).

Рис. 16.13
Лист 15. Построение четырех угольной пирамиды. Основание пирамиды квадрат со стороной 30 мм, а высота пирамиды 70 мм. Строим основание, стороны квадрата параллельны осям (см. рис. 16.14).

Рис. 16.14 Рис. 16.15
Лист 16. Находим центр основания будущей пирамиды. Для этого проводим диагонали (см. рис. 16.15).
Лист 17. Из центра основания откладываем высоту пирамиды 70 мм параллельно оси Z. Получаем вершину пирамиды (см. рис. 16.16).

Рис.16.16 Рис. 16.17
Лист 18. Соединяем вершину пирамиды с вершинами основания пирамиды (см. рис. 16.17).
Лист 19. Обводим видимые контуры пирамиды толстыми линиями (см. рис. 16.18).

Рис. 16.18 Рис. 16.19
Лист 20. Построение шестиугольной пирамиды. Диаметр основания 40 мм, высота пирамиды 70 мм (см. рис. 16.19).

Рис. 16.20 Рис. 16.21
Лист 21. Из центра основания откладываем высоту пирамиды 70 мм параллельно оси Z. Получаем вершину пирамиды (см. рис.16.20).
Лист 22. Соединяем вершину пирамиды с вершинами основания пирамиды (см. рис. 16.21).

Рис. 16.22 Рис. 16.23
Лист 23. Обводим видимые контуры пирамиды толстыми линиями (см. рис. 16.22).
Лист 24. Домашнее задание (см. рис.16.23).

Файл проекта урока для интерактивной доски MIMIO Скачать

Источник

Линейно-конструктивный рисунок шестигранной призмы

ЦЕЛЬ ЗАДАНИЯ. Научиться изображать шести­гранную призму в различных положениях.

ПОСТАНОВКА ЗАДАНИЯ. Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольни­ков постройте шестигранные призмы.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основа­нии шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — оди­наковые прямоугольники. Для того, чтобы правиль­но изобразить шестигранник в перспективе, необ­ходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифра­ми от одного до шести.

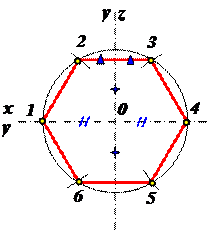
Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности де­лят диаметр 5— 2 на четыре равных отрезка (эти от­резки обозначены дугами). Противоположные сто­роны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяю­щей две вершины (например, стороны 6— 1 и 4— 3 параллельны прямой 5— 2). Эти наблюдения помо­гут вам построить шестиугольник в перспективе, а также проверить правильность этого построения.
Построить правильный шестиугольник по представ­лению можно двумя способами: на основе описан­ной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольни­ка принадлежат описанной окружности, радиус ко­торой равен стороне шестиугольника.

Горизонтальный шестиугольник

Изобразите го­ризонтальный эллипс произвольного раскрытия, т.е. описанную окружность в перспективе. Теперь необ­ходимо найти на ней шесть точек, являющихся вер­шинами шестиугольника. Проведите любой диа­метр данной окружности через ее центр (рис. 3.57).
Крайние точки диаметра — 5 и 2, лежащие на эллип­се, являются вершинами шестиугольника. Для на­хождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диа­метр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус попо­лам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины ради­усов — точки А и В — прямые, перпендикулярные пря­мой 5— 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5— 2, а прямые, проведенные через точки А и В парал­лельно этим касательным, будут также перпендику­лярны прямой 5— 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямы­ми линиями (рис. 3.61).

Проверьте правильность вашего построения разными способами. Если построение верно, то ли­нии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шести­угольника параллельны соответствующим диамет­рам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.

Вертикальный шестиугольник

В таком шести­угольнике прямые, соединяющие точки 1 и 3, 6 и 4, а также касательные к описанной окружности в точ­ках 5 и 2, имеют вертикальное направление и сохра­няют его на перспективном рисунке. Таким обра­зом, проведя две вертикальные касательные к эл­липсу, найдем точки 5 и 2 (точки касания). Соедини­те их прямой линией, а затем разделите полученный диаметр 5— 2 на 4 равных отрезка, учитывая их пер­спективные сокращения (рис. 3.65). Проведите вер­тикальные прямые через точки А и В, а на их пере­сечении с эллипсом найдите точки 7, 3, 6 и 4. Затем последовательно соедините точки 1— 6 прямыми (рис. 3.66). Правильность построения шестиуголь­ника проверьте аналогично предыдущему примеру.

Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружно­сти, изобразить которую в перспективе проще, чем
квадрат заданных пропорций. Поэтому данный спо­соб построения шестиугольника представляется наиболее точным и универсальным. Способ постро
ения на основе квадрата позволяет легко изобра­зить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизон­тальному направлению 5— 2 равен стороне квадра­та, а по вертикали — меньше ее длины.

Вертикальный шестиугольник

Нарисуйте вер­тикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5— 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68).
Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изоб­разите их на некотором расстоянии (1/14 а) от гори­зонтальных сторон квадрата и параллельно им. Со­единив найденные таким образом точки 1 и 3 с точ­кой 2, а точки 6 и 4 — с точкой 5, получим шести­угольник (рис. 3.69).

Гэризонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).

Этот способ построения уместен только для ше­стиугольников с достаточным раскрытием. В слу­чае, если раскрытие шестиугольника незначитель­но, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиуголь­ника, построенного через квадрат, можно использо­вать уже известные вам методы.

Кроме того существует еще один — описать вок­руг полученного шестиугольника окружность (на ва­шем рисунке — эллипс). Все вершины шестиуголь­ника должны принадлежать этому эллипсу.

Овладев навыками изображения шестиугольни­ка, вы свободно перейдете к изображению шести­гранной призмы. Внимательно рассмотрите схему
на рис. 3.72, а также схемы построения шестигран­ных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78).

Изобразите вертикальные и горизон­тальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник
основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке гори­зонтального шестигранника длинные стороны боко­вых граней будут сходиться в точке схода на гори­зонте, а раскрытие шестиугольника основания бу­дет тем больше, чем дальше от зрителя он находит­ся. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходи­лись в перспективе (рис. 3.79; 3.80).

Источник