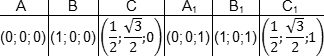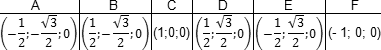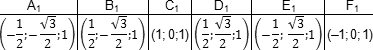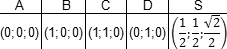Как построить призму по координатам
Введение системы координат
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Координаты куба
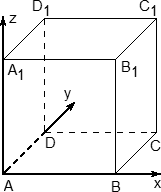
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
Координаты трехгранной призмы
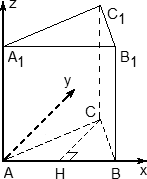
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:
Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
Получаем следующие координаты точек:
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
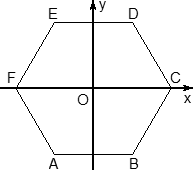
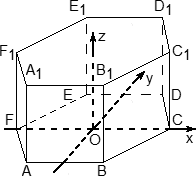
Координаты шестигранной призмы
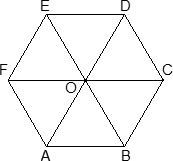
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
Координаты верхнего основания сдвинуты на единицу по оси z:
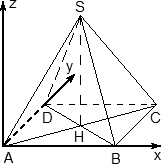
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
Комплексный чертеж призмы
Разделы: Технология
2.1. Многогранники
2.2. Сечение многогранников
2.3. Построение 6-угольной призмы с сечением фронтально-проецирующей плоскостью.
2.4. Построение развертки усеченной призмы.
Ход занятия
1. Вопросы для повторения:
Какие бывают прямые и плоскости?
— Общего и частного положения.
Как располагаются в пространстве проецирующие прямые и проецирующие плоскости?
— Они перпендикулярны плоскостям проекций.
Назовите способы преобразования чертежа.
— Способ вращения, способ перемены плоскостей проекций.
Когда применяется способ перемены плоскостей проекций?
— Когда требуется определить натуральную величину наклонного сечения для построения развертки геометрического тела.
2. Записываем новую тему “Многогранники”.
Форма многих технических деталей представляет собой сочетание простых геометрических тел. Поэтому для выполнения чертежей изделий необходимо знать, как правильно изображаются различные геометрические тела. Рассмотрим построение на комплексном чертеже основных геометрических тел: призмы, пирамиды, цилиндра, конуса, сферы, тора.
Призма.
Рассмотрим 3 проекции 6-угольной призмы. На главном виде – это прямоугольники, боковые ребра – это горизонтально проецирующие прямые, 6-угольник на виде сверху представляет собой проекцию обоих оснований.
Сечение призмы выполнено фронтально-проецирующей плоскостью.
Сечение поверхности геометрических тел плоскостью называется плоская фигура, точки которой принадлежат и поверхности тела, и секущей плоскости. Сечение широко применяется в техническом черчении для выявления формы и внутреннего устройства предметов. В сечении многогранника плоскостью образуется многоугольник. Вершины многоугольника – это точки пересечения ребер многогранника с секущей плоскостью, стороны – это линии пересечения секущей плоскости с гранями многогранника.
Рассмотрим все поставленные задачи.
Разверткой (выкройкой) поверхности тела называется плоская фигура, полученная путем совмещения всех точек данной поверхности с плоскостью без разрывов и складок.
Построение разверток выполняется обычно графическими приемами, с применением способов, предлагаемых начертательной геометрией. Построение развертки поверхности многогранника сводится к определению истинной величины каждой его грани по чертежу многогранника (см. Рис. 1). После этого грани многогранника стыкуются (соединяются) по ребрам и вершинам.
Для решения задачи 3 выполняем следующие операции:
Проводим горизонтальную прямую, на которой от произвольно выбранной точки А, откладываем отрезки AB, BC, CD, DE, EF, FA, равные длине стороны основания а = 30.
Из точек A, B, C, D, E, F, A восстанавливаем перпендикуляры и на них откладываем величины ребер усеченной призмы. Величины данных отрезков A1, B2, C3, D4, E5, F6, A1 берем с фронтальной проекции усеченной призмы. Полученные точки соединяем и получаем развертку боковой поверхности призмы.
К одному из отрезков основания, например к BC, пристраиваем 6-угольник ABCDEF.
К одному из звеньев ломаной, например, к отрезку 2-3, пристраиваем 6-угольник 123456 (сечение призмы), который переносим, используя метод засечек, с рисунка 1.
 |
Рис 1

Строим усеченную 6-и угольную призму в изометрии. Сторона основания призмы, а = 30. Для выполнения задачи учащимся раздаются трафареты 6-и угольника в изометрии. Высоты A1, B2, C3, D4, E5, F6 – берем с фронтальной проекции усеченной призмы.
Построение проекций прямой правильной призмы
Построение проекций прямой правильной призмы
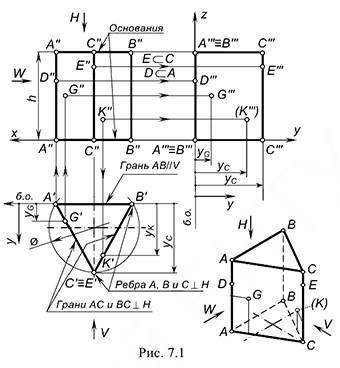
На рис. 7.1 показан пример построения проекций (очерков) прямой правильной призмы высотой 
Для построения проекций призмы требуется выполнить графоаналитические действия в следующем порядке:
1-е действие. Построить горизонтальную проекцию призмы по заданному основанию, которая представляет собой треугольник с обозначенными вершинами 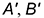
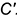
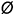
2-е действие. Выполнить графический анализ построенной горизонтальной проекции призмы:
2.1. Плоскость треугольника 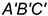
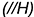
2.2. Боковые стороны 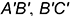
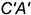

2.3. Вершины 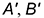
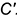
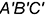
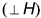
3-е действие. Построить фронтальную проекцию (очерк) призмы, которая представляет собой прямоугольник, ограниченный:
-по заданной высоте 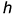
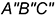
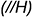
4-е действие. Выполнить графический анализ построенной фронтальной проекции призмы:
4.1. Прямоугольники 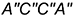
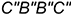
4.2. Прямоугольник 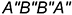
5-е действие. Построить профильную проекцию (очерк) призмы:
5.1. Задать на горизонтальной проекции призмы положение базовой линии, проходящей через заднюю грань 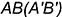
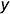
5.2. На поле чертежа справа от фронтальной проекции выбрать положение базовой оси 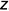
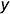
5.3. Профильная проекция призмы представляет собой прямоугольник, ограниченный:
6-е действие. Выполнить графический анализ построенной профильной проекции призмы.
6.1. Совпадающие прямоугольники 

6.2. Отрезок 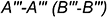
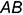
Построение горизонтальных и профильных проекций точек, лежащих на поверхности призмы
Принадлежность точек поверхности призмы определяется их принадлежностью ребрам и граням этой призмы.
На рис. 7.1 показан пример построения горизонтальных и профильных проекций точек 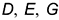
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Как построить призму по координатам

Пошаговое решение метрической задачи по начертательной геометрии МГТУ им. Баумана
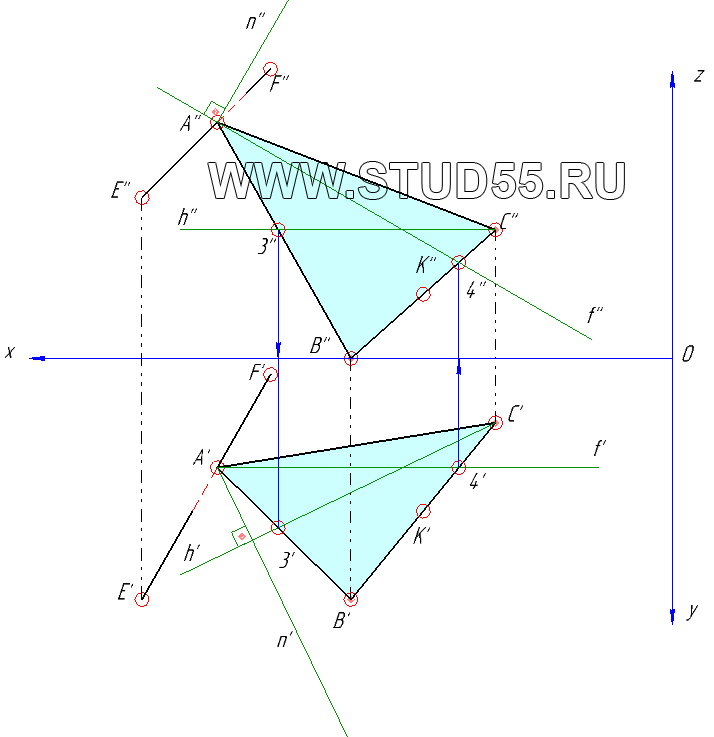
Задача 2 (вариант 19)
ПОСТРОИТЬ ПРОЕКЦИИ ПРЯМОЙ ПРИЗМЫ АВСА1В1С1,
при условии, что её высота равна 70 мм., а в основании лежит равнобедренный треугольник ABC (АВ=АС) с вершиной А на прямой EF.
Решить без преобразования чертежа.
Решение задачи по начертательной геометрии:
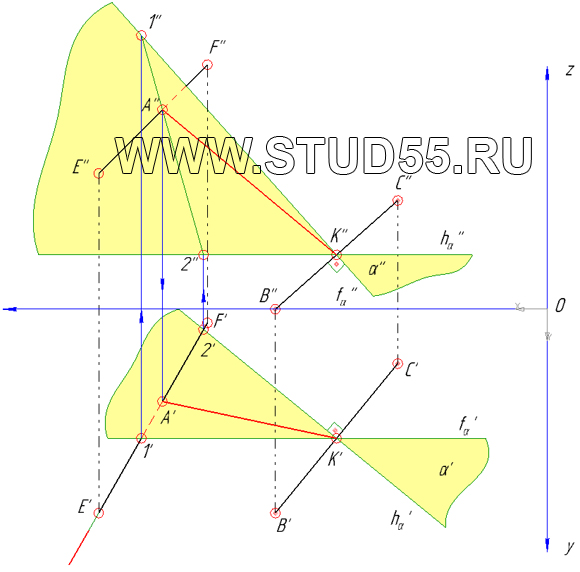
1) Проекции точки К получаем просто разделив СВ на 2 равные части: СК=КВ
2) Далее нам необходимо построить плоскость a (альфа) перпендикулярную отрезку СВ в точке К,
СВ занимает общее положение в пространстве, поэтому начать ее построение можно в горизонтальной плоскости проекций,
для этого проводим через точку К — фронтальный луч f ‘ параллельно х и горизонтальный h ‘ перпенд. С’K’
Следовательно, во фронтальной плоскости проекций искомая плоскость альфа будет задана лучами f » перпенд. С»K» и
горизонтальным h ‘» параллельным оси х.
3) Теперь мы можем определить точку А пересечения построенной плоскости альфа с отрезком EF. Для этого через EF (E’F’)
проводим горизонтально проецирующую плоскость перпендикулярную горизонт. плоскости проекций, отмечаем на лучах
проекции f ‘ точку — 1′ и на h ‘ — 2′. По линиям связи переносим на фронтальную плоскость и получаем фронтальную проекцию
отрезка 1-2 (1»2»).
4) В точке пересечения 1»2» и E»F» — находим проекцию точки пересечения плоскости альфа и EF — A», по линии связи находим
горизонтальную проекцию точки А (A’).
5) Если соединить точки А и К, то получим отрезок АК, который будет принадлежать плоскости альфа, Т.к. он принадлежит
плоскости альфа и альфа перпендикулярна СВ, следовательно,
и отрезок АК будет перпендикулярен СВ. Следовательно отрезки АС и СВ будут равноудалены от точки А и мы находим
основание нашей призмы в основании которой будет равнобедренный треугольник АВС с АС=АВ.
6) Т.к. призма прямая, следовательно, ребра призмы должны быть перпедикулярны основанию АВС. Построим перпендикуляр n к АВС из точки А, для
этого проведем фронталь f и горизонталь h плоскости АВС. Далее строим n’ перпенд. h’ и n» перпенд. f».
7) Далее нам необходимо на перпендикуляре n отложить ребро АА10=70 мм. Для этого на n возьмем произвольную точку H — H» и H’, и определим натуральную величину отрезка АН способом прямоугольного треугольника, для этого из проекции H’ под прямым углом к n’ отложим разницу высот точек А и Н. На A’H0 — будет натуральной величиной отрезка АН.
8) На A’H откладываем отрезок равный 70 мм от А’ и по линии связи находим вершину призмы A1‘, получаем проекцию ребра A’A’1, и по линии связи на n» получаем A1‘’ — и ребро A»A1»
9) Достраиваем ребра, получаем 2 проекции нашей искомой призмы. С помощью 2-ух пар конкурирующих точек 5 6 и 7 8, определяем видимость всех ребер призмы.
Лекция 6. Многогранники
6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды
Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.
Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.
Упражнение
Дана пирамида, основание которой параллельно π1. Основание представляет собой некоторый треугольник.
S – вершина пирамиды (Рисунок 6.1). 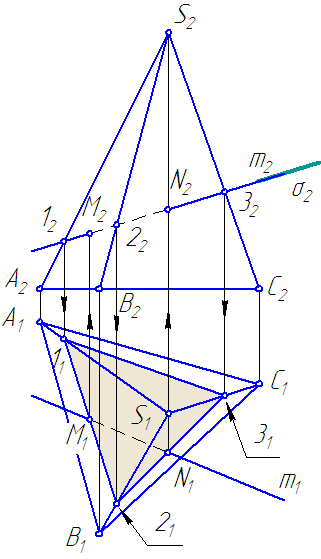
Рисунок 6.1 – Пересечение поверхности пирамиды прямой
Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.
Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).
Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.
Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.
Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.
Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.
Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).
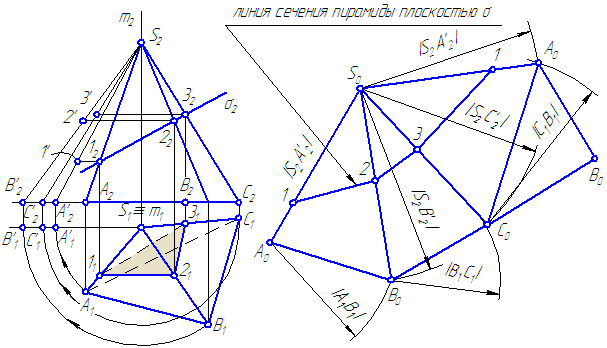
Рисунок 6.2 – Построение развёртки пирамиды
В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки \overline<1>,\overline<2>,\overline <3>, проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.
6.2. Призма. Развертка призмы
Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.
Упражнение
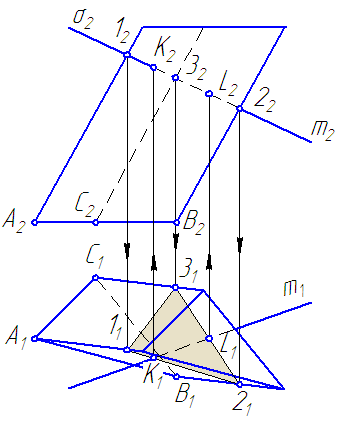
Дана призма, основания которой параллельны плоскости проекций π1.
Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).
Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы
Рассмотрим наклонную призму. Пусть основание призмы параллельно π1, а ребра параллельны π2.
Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).
Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.
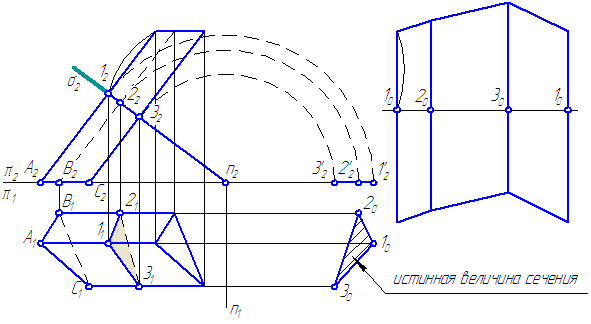
Рисунок 6.4 – Построение развёртки призмы
Порядок построения :
6.3. Взаимное пересечение многогранников
В результате пересечения многогранников получим ломаную линию.
Возможны два случая пересечения многогранников (Рисунок 6.5):
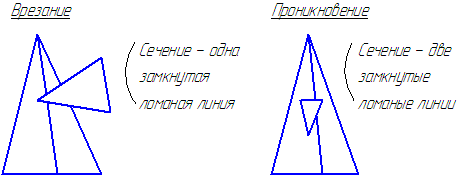
Рисунок 6.5 – Варианты пересечения многогранников
Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.
Звенья ломаной – линии пересечения граней.
Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.
Построенные точки соединить.
Упражнение
Построить линии пересечения призмы с пирамидой (Рисунок 6.6). 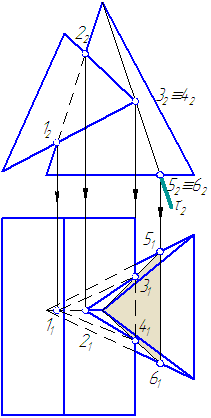
Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение
Упражнение
остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).
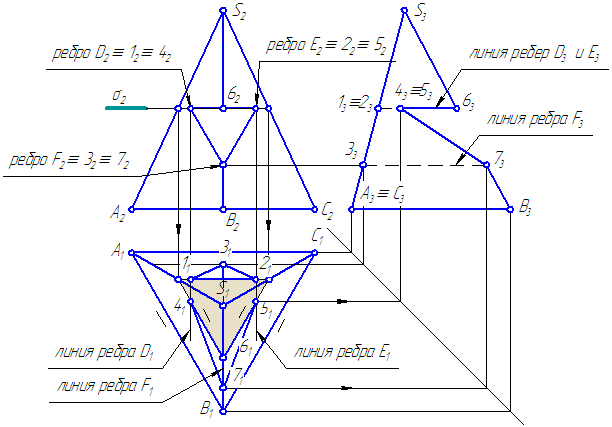
Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение :
Это сечение пересекается:
— с ребром D в двух точках 1 и 4;
— с ребром Е в двух точках 2 и 5.
Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.
Построение развертки рассмотрено ранее.
6.4. Задачи для самостоятельной работы
1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).
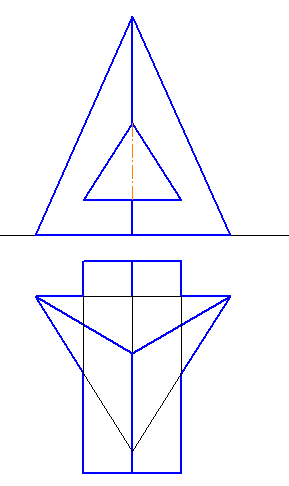
Рисунок 6.8 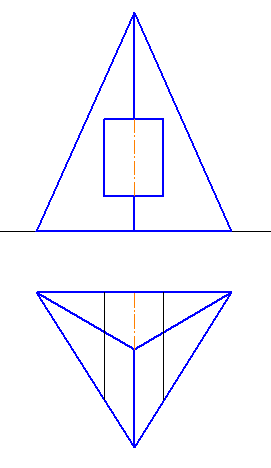
Рисунок 6.9 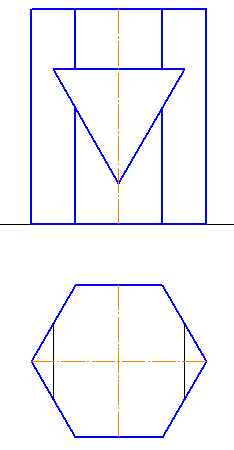
Рисунок 6.10 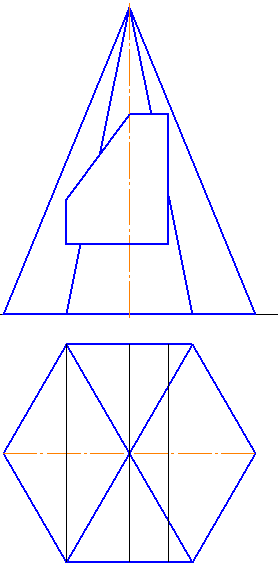
Рисунок 6.11