Как построить ось симметрии луча

Осевая и центральная симметрия

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

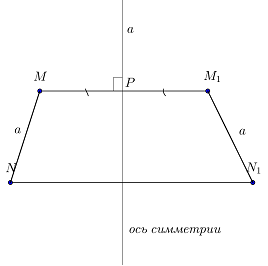
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник

Что называется осевой симметрией

Что такое осевая симметрия в геометрии

Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.

Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – S_n, таким образом симметрия точек A и B обозначается так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.

Свойства осевой симметрии

Теорема и доказательство

Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.

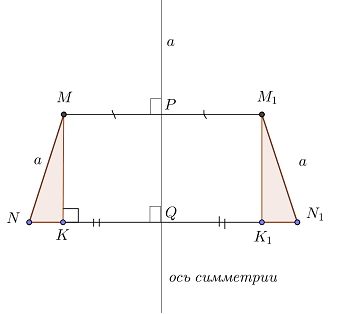
Если отрезок MN симметричен отрезку M₁N₁ относительно прямой a, то MN = M₁N₁.

Чтобы доказать, что MN = M₁N₁, сделаем дополнительные построения:

Докажем, что прямоугольные треугольники MNK и M₁N₁K₁ равны. Стороны MN и M₁N₁ являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.

Точка N отобразилась в точку N₁, значит:

Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M₁N₁, что и требовалось доказать.

Фигуры, обладающие симметрией

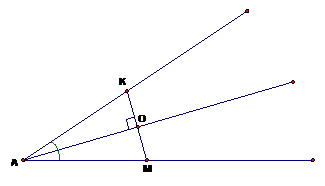
Осевой симметрией обладает угол, а биссектриса является осью симметрии.

Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:

Рассмотрим Δ KAO и Δ MAO:

Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.

Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.

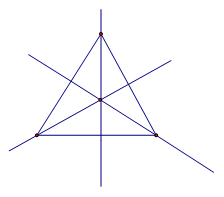
Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:

У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.

Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.

Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.

У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.

Источник

Как построить ось симметрии луча

На этом уроке мы рассмотрим ещё одну характеристику некоторых фигур – осевую и центральную симметрию. С осевой симметрией мы сталкиваемся каждый день, глядя в зеркало. Центральная симметрия очень часто встречается в живой природе. Вместе с тем, фигуры, которые обладают симметрией, имеют целый ряд свойств. Кроме того, впоследствии мы узнаем, что осевая и центральная симметрии являются видами движений, с помощью которых решается целый класс задач.

Данный урок посвящён осевой и центральной симметрии.

Определение

Две точки и называются симметричными относительно прямой , если:

1. прямая проходит через середину отрезка ;

2. прямая перпендикулярна отрезку.

На Рис. 1 изображены примеры симметричных относительно прямой точек и , и .

Отметим также тот факт, что любая точка прямой симметрична сама себе относительно этой прямой.

Симметричными относительно прямой могут быть и фигуры.

Сформулируем строгое определение.

Определение

Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей относительно этой прямой точка также принадлежит фигуре. В этом случае прямая называется осью симметрии. Фигура при этом обладает осевой симметрией.

Рассмотрим несколько примеров фигур, обладающих осевой симметрией, и их оси симметрии.

Пример 1

Угол обладает осевой симметрией. Осью симметрии угла является биссектриса. Действительно: опустим из любой точки угла перпендикуляр к биссектрисе и продлим его до пересечения с другой стороной угла (см. Рис. 2).

(так как – общая сторона, (свойство биссектрисы), а треугольники – прямоугольные). Значит, . Поэтому точки и симметричны относительно биссектрисы угла.

Из этого следует, что и равнобедренный треугольник обладает осевой симметрии относительно биссектрисы (высоты, медианы), проведённой к снованию.

Пример 2

Равносторонний треугольник обладает тремя осями симметрии (биссектрисы/медианы/высоты каждого из трёх углов (см. Рис. 3).

Пример 3

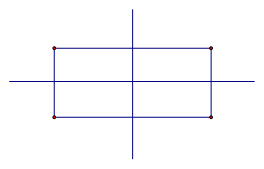
Прямоугольник обладает двумя осями симметрии, каждая из которых проходит через середины двух его противоположных сторон (см. Рис. 4).

Пример 4

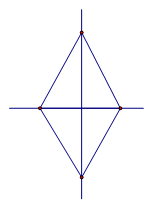
Ромб также обладает двумя осями симметрии: прямые, которые содержат его диагонали (см. Рис. 5).

Пример 5

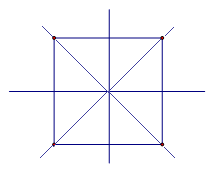
Квадрат, являющийся одновременно ромбом и прямоугольником, обладает 4 осями симметрии (см. Рис. 6).

Пример 6

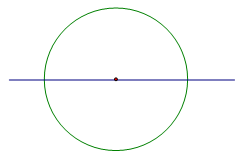
У окружности осью симметрии является любая прямая, проходящая через её центр (то есть содержащая диаметр окружности). Поэтому окружность имеет бесконечно много осей симметрии (см. Рис. 7).

Рассмотрим теперь понятие центральной симметрии.

Определение

Точки и называются симметричными относительно точки , если: – середина отрезка .

Рассмотрим несколько примеров: на Рис. 8 изображены точки и , а также и , которые являются симметричными относительно точки , а точки и не являются симметричными относительно этой точки.

Некоторые фигуры являются симметричными относительно некоторой точки. Сформулируем строгое определение.

Определение

Фигура называется симметричной относительно точки , если для любой точки фигуры точка, симметричная ей, также принадлежит данной фигуре. Точка называется центром симметрии, а фигура обладает центральной симметрией.

Рассмотрим примеры фигур, обладающих центральной симметрией.

Пример 7

У окружности центром симметрии является центр окружности (это легко доказать, вспомнив свойства диаметра и радиуса окружности) (см. Рис. 9).

Пример 8

У параллелограмма центром симметрии является точка пересечения диагоналей (см. Рис. 10).

Решим несколько задач на осевую и центральную симметрию.

Задача 1.

Сколько осей симметрии имеет отрезок ?

Отрезок имеет две оси симметрии. Первая из них – это прямая, содержащая отрезок (так как любая точка прямой симметрична сама себе относительно этой прямой). Вторая – серединный перпендикуляр к отрезку, то есть прямая, перпендикулярная отрезку и проходящая через его середину.

Ответ: 2 оси симметрии.

Задача 2.

Сколько осей симметрии имеет прямая ?

Прямая имеет бесконечно много осей симметрии. Одна из них – это сама прямая (так как любая точка прямой симметрична сама себе относительно этой прямой). А также осями симметрии являются любые прямые, перпендикулярные данной прямой.

Ответ: бесконечно много осей симметрии.

Задача 3.

Сколько осей симметрии имеет луч ?

Луч имеет одну ось симметрии, которая совпадает с прямой, содержащей луч (так как любая точка прямой симметрична сама себе относительно этой прямой).

Ответ: одна ось симметрии.

Задача 4.

Доказать, что прямые, содержащие диагонали ромба, являются его осями симметрии.

Рассмотрим ромб . Докажем, к примеру, что прямая является его осью симметрии. Очевидно, что точки и являются симметричными сами себе, так как лежат на этой прямой. Кроме того, точки и симметричны относительно этой прямой, так как . Выберем теперь произвольную точку и докажем, что симметричная ей относительно точка также принадлежит ромбу (см. Рис. 11).

Проведём через точку перпендикуляр к прямой и продлим его до пересечения с . Рассмотрим треугольники и . Эти треугольники прямоугольные (по построению), кроме того, в них: – общий катет, а (так как диагонали ромба являются его биссектрисами). Значит, эти треугольники равны: . Значит, равны и все их соответствующие элементы, поэтому: . Из равенства этих отрезков следует то, что точки и являются симметричными относительно прямой . Это означает, что является осью симметрии ромба. Аналогично можно доказать этот факт и для второй диагонали.

Задача 5.

Доказать, что точка пересечения диагоналей параллелограмма является его центром симметрии.

Рассмотрим параллелограмм . Докажем, что точка является его центром симметрии. Очевидно, что точки и , и являются попарно симметричными относительно точки , так как диагонали параллелограмма точкой пересечения делятся пополам. Выберем теперь произвольную точку и докажем, что симметричная ей относительно точка также принадлежит параллелограмму (см. Рис. 12).

Соединим точку с точкой и продлим линию до пересечения с противоположной стороной. Рассмотрим треугольники и . Эти треугольники равны по второму признаку равенства треугольников (сторона и два угла). Действительно: (так как диагонали параллелограмма точкой пересечения делятся пополам), (как внутренние накрест лежащие при параллельных прямых), (как вертикальные углы). Значит, эти треугольники равны: . Значит, равны и все их соответствующие элементы, поэтому: . Из равенства этих отрезков следует то, что точки и являются симметричными относительно точки . Это означает, что является центром симметрии параллелограмма.

На этом уроке мы заканчиваем изучение темы «виды четырёхугольников» (параллелограмм, трапеция, прямоугольник, ромб, квадрат). Мы рассмотрели осевую и центральную симметрию и её примеры для различных геометрических фигур. Кроме того, были решены несколько задач на эту тему.

На следующих уроках мы перейдём к изучению новой темы: «Площадь».

Список литературы

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Источник