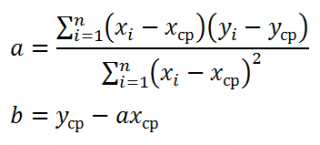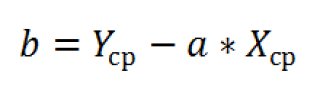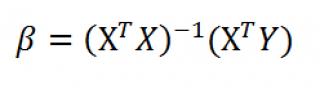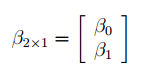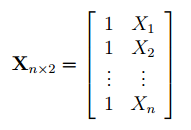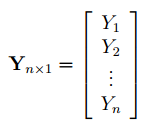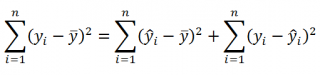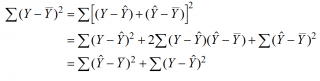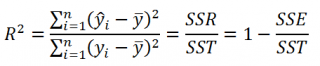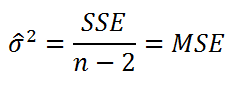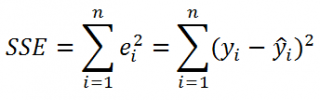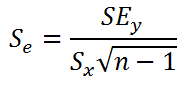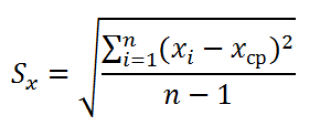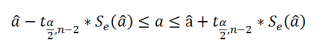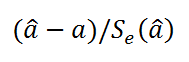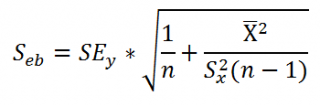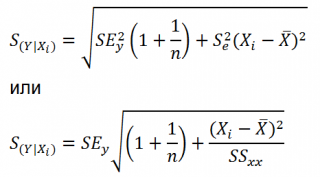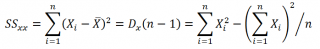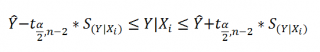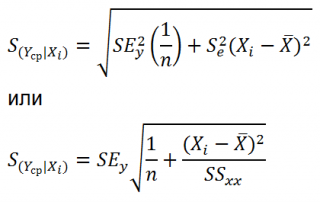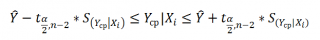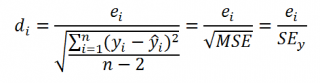Как построить модель в excel
Создание модели данных в Excel
Модель данных позволяет интегрировать данные из нескольких таблиц, эффективно построение источника реляционных данных Excel книге. В Excel данных модели данных применяются прозрачно, что обеспечивает табличные данные, используемые в сводных таблицах и на сводных таблицах. Модель данных визуализируются как набор таблиц в списке полей, и в большинстве моментов вы даже не узнаете, что она там.
Прежде чем приступить к работе с моделью данных, необходимо получить некоторые данные. Для этого мы используем power query & Transform ( Get & Transform), чтобы вы могли захотеть вернуться на шаг назад и посмотреть видео или воспользоваться учебным руководством по & Преобразование и Power Pivot.
Excel 2016 & Excel для Microsoft 365 — На ленте есть Power Pivot.
Excel 2013 — Power Pivot входит в выпуск Office профессиональный плюс версии Excel 2013, но по умолчанию не включен. Подробнее о запуске надстройки Power Pivot для Excel 2013.
Excel 2010 — скачайте надстройку Power Pivot, а затем установите надстройку Power Pivot,
Excel 2016 & Excel для Microsoft 365 — & Power Query интегрирован с Excel на вкладке Данные.
Excel 2010— скачивание и установка надстройки Power Query.. После активации на ленту будет добавлена вкладка Power Query.
Начало работы
Во-первых, вам нужно получить некоторые данные.
В Excel 2016 и Excel для Microsoft 365 используйте data > Get & Transform Data > Get Data (Получить данные), чтобы импортировать данные из любого числа внешних источников данных, таких как текстовый файл, книга Excel, веб-сайт, Microsoft Access, SQL Server или другая реляционная база данных, которая содержит несколько связанных таблиц.
В Excel 2013 и 2010 перейдите в Power Query > Получитьвнешние данные и выберите источник данных.
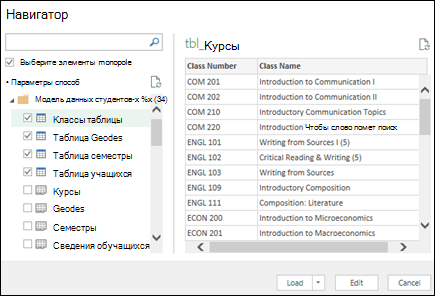
Excel предложит выбрать таблицу. Если вы хотите получить несколько таблиц из одного источника данных, проверьте параметр Включить выбор нескольких таблиц. При выборе нескольких таблиц Excel автоматически создает модель данных.
Примечание: В этих примерах мы используем книгу Excel с вымышленными сведениями об учащихся в классах и оценках. Вы можете скачать образец книги модели данныхдля учащихся и следуйте этим командам. Вы также можете скачать версию с завершенной моделью данных..
Выберите одну или несколько таблиц и нажмите кнопку Загрузить.
Если вам нужно изменить исходные данные, можно выбрать параметр Изменить. Дополнительные сведения см. в обзоре редактора запросов (Power Query).
Теперь у вас есть модель данных, которая содержит все импортируемые таблицы, и они будут отображаться в списке полей таблицы.
Модели создаются неявно, когда вы импортируете в Excel несколько таблиц одновременно.
Модели создаются явно, если вы импортируете данные с помощью надстройки Power Pivot. В надстройке модель представлена в макете со вкладками так же, как Excel, где каждая вкладка содержит табличные данные. Сведения о том,как импортировать данные с помощью базы данных, см. в этой SQL Server Power Pivot.
Модель может содержать одну таблицу. Чтобы создать модель на основе только одной таблицы, выберите таблицу и нажмите кнопку Добавить в модель данных в Power Pivot. Это может понадобиться в том случае, если вы хотите использовать функции Power Pivot, например отфильтрованные наборы данных, вычисляемые столбцы, вычисляемые поля, ключевые показатели эффективности и иерархии.
Связи между таблицами могут создаваться автоматически при импорте связанных таблиц, у которых есть связи по первичному и внешнему ключу. Excel обычно может использовать импортированные данные о связях в качестве основы для связей между таблицами в модели данных.
Советы по уменьшению размера модели данных см. в Excel и Power Pivot.
Дополнительные сведения см. в учебнике Импорт данных в Excel и Создание модели данных.
Совет: Как узнать, есть ли в книге модель данных? Перейдите в Power Pivot > Управление. Если вы видите данные, похожие на таблицу, то модель существует. Дополнительные сведения см. в этой теме.
Создание связей между таблицами
Далее нужно создать связи между таблицами, чтобы можно было извлекть данные из любой из них. Каждая таблица должна иметь первичный ключ или уникальный идентификатор поля, например Код учащегося или номер класса. Проще всего перетащить эти поля, чтобы соединить их в представлении диаграммы Power Pivot.
На вкладке Главная выберите представление диаграммы.
Будут показаны все импортируемые таблицы, и вам может потребоваться некоторое время, чтобы их можно было отобразить в зависимости от их количество.
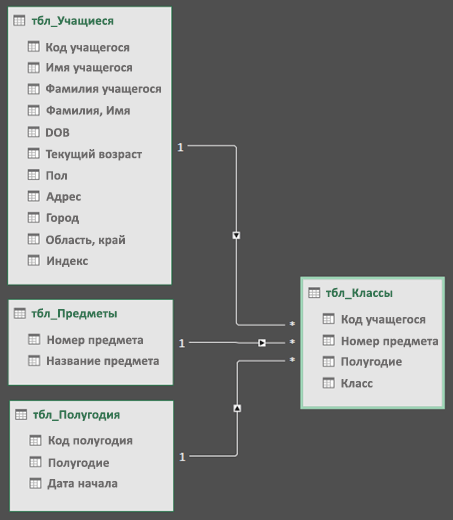
Затем перетащите поле первичного ключа из одной таблицы в следующую. Ниже приведен пример представления диаграммы таблиц наших учащихся:
Мы создали следующие ссылки:
tbl_Students | ИД учащегося > tbl_Grades | ИД учащегося
Другими словами, перетащите поле «ИД учащегося» из таблицы «Учащиеся» в поле «ИД учащегося» в таблице «Оценки».
tbl_Semesters | ИД семестра > tbl_Grades | Семестр
tbl_Classes | Номер > tbl_Grades | Номер класса
Имена полей не должны быть одинаковыми для создания связи, но они должны быть одного типа данных.
Соединители в представлении диаграммы имеют 1 с одной стороны, а «*» — на другой. Это означает, что между таблицами существует связь «один-к-многим», которая определяет способ использования данных в таблицах. Дополнительные сведения см. в этой теме: Связи между таблицами в модели данных.
Соединитетели указывают только на связь между таблицами. Они не будут показывать, какие поля связаны друг с другом. Чтобы увидеть ссылки, перейдите в Power Pivot > Управление > конструктором > связи > Управление связями. В Excel вы можете перейти к data > Relationships (Отношения > данных).
Создание и создание с помощью модели данных для создания сводная диаграмма
Книга Excel может содержать только одну модель данных, но она содержит несколько таблиц, которые можно многократно использовать во всей книге. Вы можете добавить дополнительные таблицы в существующую модель данных в любое время.
На вкладке Главная выберите вкладку «PivotTable».
Выберите место для размещения таблицы: новый или текущий.
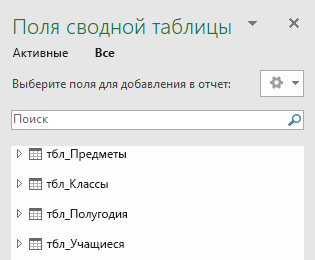
Нажмите кнопкуОК, Excel и справа отобразит пустую с помощью области Список полей пустую.
Затем создайте или создайтесетовую диаграмму. Если вы уже создали связи между таблицами, вы можете использовать любое из их полей в таблице. Мы уже создали связи в образце книги модели данных для учащихся.
Добавление имеющихся несвязанных данных в модель данных
Предположим, вы импортировали или скопировали много данных, которые вы хотите использовать в модели, но не добавили их в модель данных. Принудительно отправить новые данные в модель очень просто.
Сначала выберите любую ячейку в данных, которые вы хотите добавить в модель. Это может быть любой диапазон данных, но лучше всего отформатированные как Excel таблицы.
Добавьте данные одним из следующих способов.
Щелкните Power Pivot > Добавить в модель данных.
Выберите Вставка > Сводная таблица и установите флажок Добавить эти данные в модель данных в диалоговом окне «Создание сводной таблицы».
Диапазон или таблица будут добавлены в модель как связанная таблица. Дополнительные сведения о работе со связанными таблицами в модели см. в статье Добавление данных с помощью связанных таблиц Excel в Power Pivot.
Добавление данных в Power Pivot таблицу
В Power Pivot невозможно добавить строку в таблицу, введя текст непосредственно в новой строке, как это можно сделать на листе Excel. Но вы можете добавить строки, скопируяи впав их или обновив исходные данные и обновив модель Power Pivot.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Пример построения финансовой модели предприятия в Excel
Любой бизнес-план нуждается в финансовых расчетах. А наиболее удобный инструмент для этого – табличный процессор Excel. Популярность программы объясняется простотой использования и многофункциональностью. Рассмотрим возможности редактора, которые будут полезны при составлении бизнес-модели.
Основы построение финансовой модели в Excel
Модель можно поместить на один лист или на разные листы. В любом случае, порядок расчетных таблиц должен соответствовать логике описания проекта:
Инвестиционный план
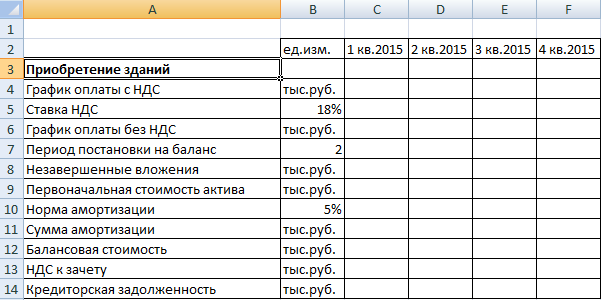
Исходные данные для расчета затрат на покупку или строительство зданий:
Затраты на приобретение оборудования и элементы расходов будущих периодов в инвестиционном плане составляются аналогично. Особенности затрат будущих периодов:
Прогнозирование доходов
Чтобы построить план продаж, нужно определить объем в натуральном выражении (для каждого вида продукции) и цену реализации (каждого вида продукции). Выручка определяется по каждому виду товара (работ и услуг) как произведение объема и цены.
В Excel составляются таблицы для каждого периода планирования и для каждого вида продукции с планируемым объемом выпуска (в натуральных единицах).
Из цены реализации нужно вычленять сумму налога на добавленную стоимость. Эти деньги не входят в состав выручки – они перечисляются в бюджет.
Расчетная таблица может выглядеть следующим образом:
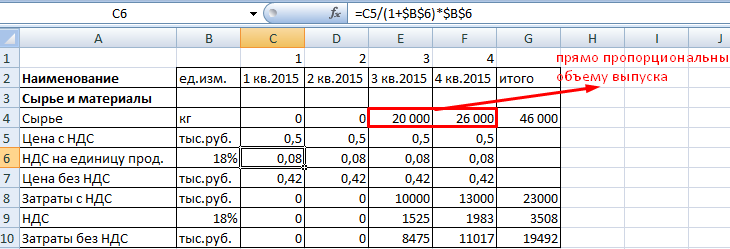
План текущих расходов
При учете затрат на материалы выделяем налог добавленной стоимости. Это необходимо для учета подлежащих возврату сумм (задолженность перед бюджетом уменьшится).
Затраты на сырье и материалы увеличиваются прямо пропорционально объему выпуска. Если, к примеру, на пошив одной сорочки требуется полтора метра ткани, то на две единицы продукции – 3 метра и т.д. Расход считается по формуле:
Количество материалов = удельный вес * объем производства.
Пример таблицы учета текущих затрат на сырье и материалы:
Формула для расчета налога на добавленную стоимость – в строке формул.
Формула вычисления цены без НДС: =C5/(1+$B$6).
Расчет затрат с НДС: =C4*C5.
Затраты без НДС: =C4*C7.
При составлении финансовой модели предприятия в Excel учитывается каждая статья расходов.
Финансовая модель предприятия в Excel
Когда спланированы продажи и затраты, можно приступать к формированию баланса, плана доходов и расходов, движения денежных средств. Чтобы модель пересчитывала значения в автоматическом режиме, данные в сводных отчетах рассчитываются с помощью формул или напрямую извлекаются из операционных планов (с помощью ссылок).
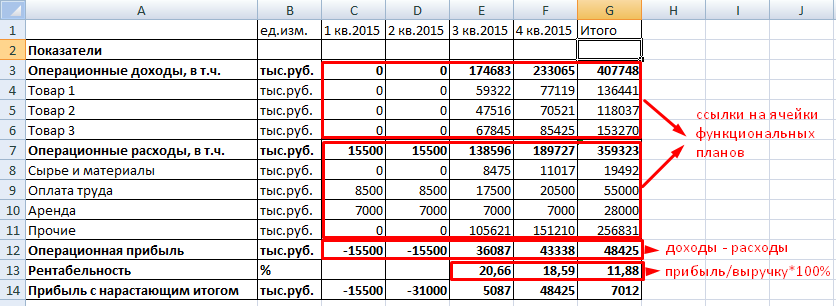
План доходов и расходов финансовой модели:
Доходы и расходы расписаны по статьям. Если планируется выпуск десятков наименований продукции, то лучше определить их в группы. Чтобы не перегружать отчет. В сводную таблицу добавлены аналитические показатели: рентабельность и прибыль с нарастающим итогом. Когда нужно больше аналитики, формируют отдельные таблицы.
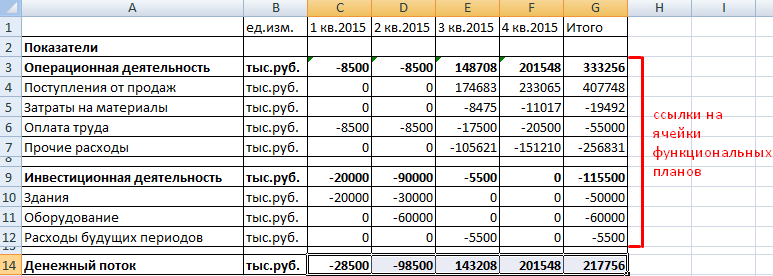
План движения денежных средств:
Предполагается, что предприятие не будет привлекать заемные средства. Поэтому раздел «Финансовая деятельность» отсутствует.
Как в офисе.
Моделирование в электронных таблицах
Разделы: Информатика
Урок № 1. Задача о попадании точки в заданную фигуру. 2 часа.
Цель урока: построить в Excel компьютерную модель заданной на плоскости фигуры, исследовать ее, вводя координаты различных точек.
Учащиеся должны уметь: строить чертеж в Word, строить математическую модель фигуры, строить компьютерную модель в Excel.
Решение задачи о попадании точки в фигуру на примерах с использованием логических функций Excel. 40 мин.
Практическая работа: решить задачу для заданной фигуры в Excel, построить чертеж фигуры в Word, построить математическую модель, построить компьютерную модель, вставить решение из Excel в Word как объект с целью дальнейшего тестирования и проверки задачи. 40 мин.
Домашнее задание: построить математическую и компьютерную модель (программа на Паскале) для заданной фигуры.
Математическая модель: рис. 2
Компьютерная модель:
Рассмотрим еще один пример: рис 3. Разделим фигуру на две части.
Математическая модель: 1 часть: рис. 4 2 часть: рис. 5
=ЕСЛИ(ИЛИ(И(A2>=-2; А2 =0;B2 =0;B2>=0));»попадает»;»не попадает«)
Для вставки объекта Excel в документ Word необходимо:
сохранить решение задачи в Excel;
в документе Word установить курсор на место вставки;
Вставка — Объект — создать из файла — Обзор — Найти файл с решением задачи — Вставить.
Учащимся выдаются заранее подготовленные карточки с различными фигурами.
Цель урока: построить имитационную модель игры.
Учащиеся должны знать: понятие модели, случайного процесса, формализации, информационной модели, компьютерной модели, основные приемы работы в Excel, логические функции Excel, функцию случайных чисел.
Учащиеся должны уметь: работать с электронной таблицей, проводить формализацию задачи, строить информационную и компьютерную модель задачи.
Разбор задачи «Кубики» и задачи о проверке знания таблицы умножения — объяснение у доски (40 мин).
Самостоятельная работа: задача «Домино» — работа за компьютером (40 мин).
Задача «Кубики».
Смоделируйте игру «Кубики»: двое игроков бросают игральный кубик. Определить результат игры.
Выходные параметры : результат — кто победил.
Связь: если х>у, то победил первый игрок, иначе если х=у, то — ничья, иначе — победил второй игрок. Можно связь представить в виде блок-схемы.
Очки, выпавшие у первого и второго игрока, выводятся только после введения имен игроков. Очистка таблицы производится клавишей F9.
В ячейке первого игрока формула:
В ячейке второго игрока формула:
В ячейке результата формула:
=ЕСЛИ(ИЛИ(ЕПУСТО(B2);ЕПУСТО(B4));»»;ЕСЛИ(B3>B5;»выиграл первый»;ЕСЛИ(B3 Постановка задачи.
Смоделируйте работу программы проверки знания таблицы умножения.
Входные параметры: х,у — сомножители, р — ответ, вводимый учеником.
Связь: если р=х*у, то результат — сообщение: ответ правильный, иначе — результат: сообщение об ошибке. Связь также можно представить в виде блок-схемы.
Для вычисления сомножителей применяются формулы:
Для проверки результата используется формула:
Выходные параметры: ответ: можно приставить кости одну к другой или нет.
Связь: если х1=х2 или х1=у2 или у1=х2 или у1=у2, то ответ: можно, иначе — ответ: нельзя. Связь можно представить в виде блок-схемы.
Для получения значений «костей» домино используются формулы:
Для определения результата используется формула:
Урок № 3. Моделирование биоритмов. 2 часа.
Цель урока: составить модель биоритмов для каждого учащегося от указанной текущей даты на месяц вперед для дальнейшего анализа модели, построить суммарные биоритмы для определения совместимости двух человек.
Учащиеся должны знать: понятие модели, биоритмов.
Постановка задачи. 5 мин.
Математическая модель. 5 мин.
Построение компьютерной модели в среде Excel. 20 мин.
Анализ результатов моделирования. 10 мин.
Построение суммарных биоритмов. 20 мин.
Оформление работы. 20 мин.
Домашнее задание: построить биоритмы на текущий месяц членам своей семьи.
Постановка задачи.
За точку отсчета всех биоритмов берется день рождения человека. В этот момент все три биоритма пересекают ось абсцисс, т.к. процесс появления на свет очень труден для человека, ведь происходит смена водной среды на воздушную. Происходит глобальная перестройка всего организма.
Физический биоритм характеризует жизненные силы человека. Периодичность ритма составляет 23 дня.
Эмоциональный биоритм характеризует внутренний настрой человека, его возбудимость, способность эмоционального восприятия окружающего. Продолжительность периода эмоционального цикла равна 28 дням.
Третий биоритм характеризует мыслительные способности, интеллектуальное состояние человека. Его цикличность — 33 дня.
Физический цикл F(x)=sin
Эмоциональный цикл F(x)=sin
Интеллектуальный цикл F(x)=sin, где х — возраст человека в днях.
Компьютерная модель.
Формулы для расчета кривых:
В ячейке А3 находится дата рождения, в ячейке В3 — первое число расчетного периода.
Физическое состояние Эмоциональное состояние Интеллект. состояние
Проанализировав диаграмму, выбрать неблагоприятные дни для сдачи зачета по физкультуре.
Выбрать день для похода в цирк.
Выбрать дни, когда ответы на уроках будут наиболее (наименее) удачными.
Как вы думаете, что будет показывать график, если сложить все три биоритма? Можно ли будет по нему что-либо определить?
Построить модель физической, эмоциональной и интеллектуальной совместимости двух друзей.
Что показывают суммарные графики одноименных биоритмов? Что можно по ним определить?
Какая из трех кривых показывает наилучшую (наихудшую) совместимость с другом?
Выбрать наиболее благоприятные дни для совместного участия с другом в командной игре, например в футбольном матче. Можно ли вообще вам с другом выступать в соревнованиях единой командой? Ответ обоснуйте.
Определите дни, когда вам не следует общаться. Что можно ожидать в эти дни?
Спрогнозировать результат совместного с другом разгадывания кроссворда в указанные дни месяца, например, 10-го, 15-го и 21-го.
В какой области совместной деятельности вы с другом могли бы преуспеть?
Не закрывая Excel, открыть документ Word. Скопировать в него обе диаграммы (собственных и суммарных биоритмов). Ответы на вопросы оформить в виде списка с ответами по собственным и суммарным биоритмам. Сохранить текстовый файл на учительском компьютере (файл — сохранить как — мое сетевое окружение — соседние компьютеры — Teacher — Мои документы).
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Теперь стали видны и данные регрессионного анализа.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
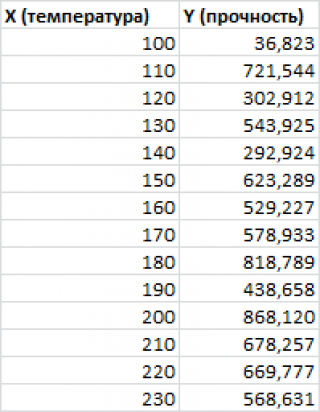
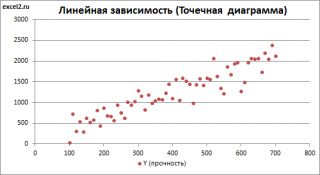
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
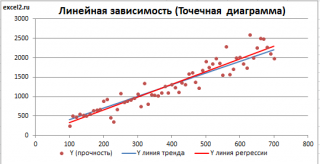
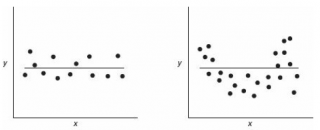
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Подобные рассуждения можно привести для любого значения Хi.
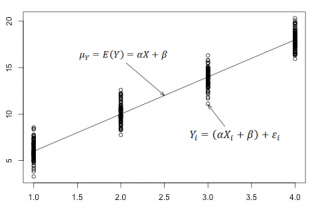
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Задачи регрессионного анализа
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Оценку параметров в MS EXCEL можно выполнить различными способами:
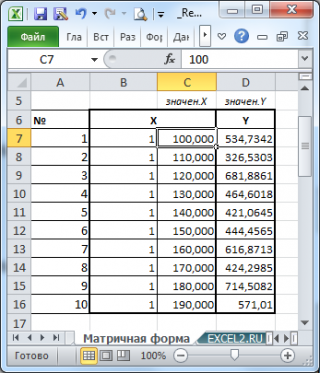
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Чтобы вывести сразу обе оценки:
Оценка неизвестных параметров линейной модели (через статистики выборок)
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
В формуле символом Y обозначен столбец значений переменной Y.
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Построение линии регрессии
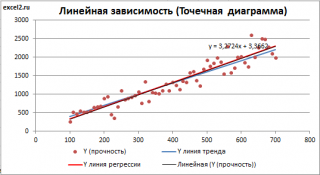
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Коэффициент детерминации R 2
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
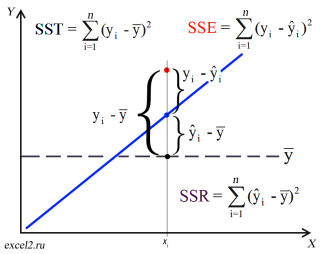
Очевидно, что все три ошибки связаны выражением:
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Для оценки дисперсии σ 2 используют следующую формулу:
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
или с помощью функции ЛИНЕЙН() :
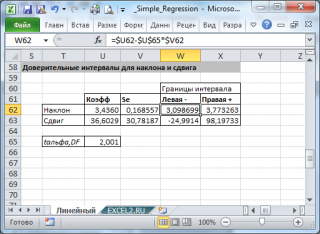
Стандартные ошибки и доверительные интервалы для наклона и сдвига
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
или с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
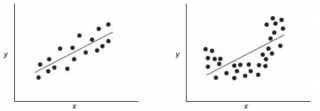
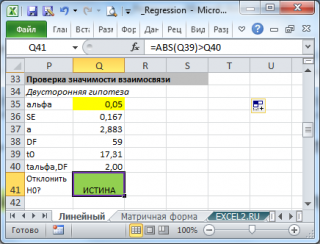
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
Для проверки гипотезы нам потребуется:
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
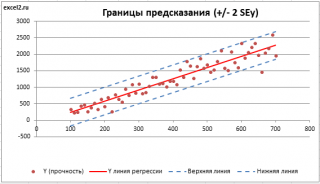
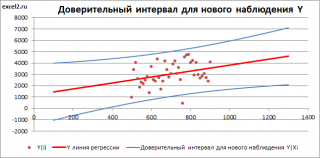
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
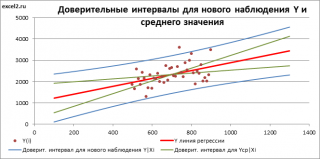
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
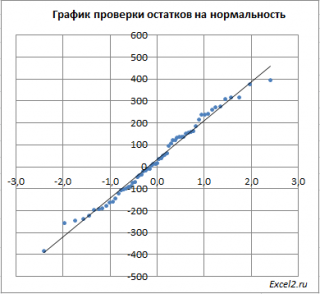
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
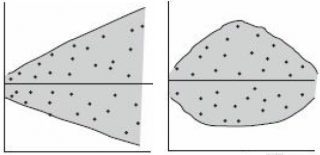
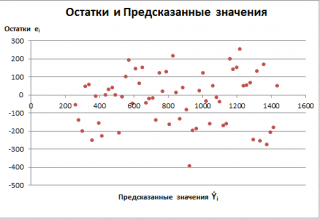
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.