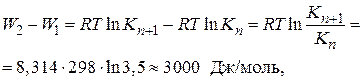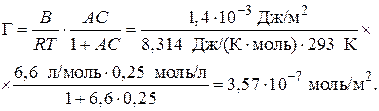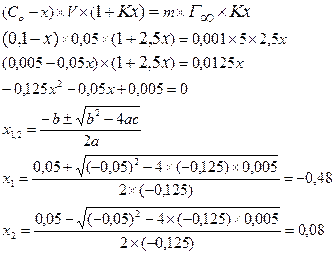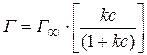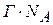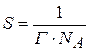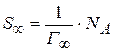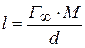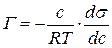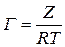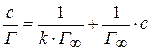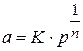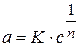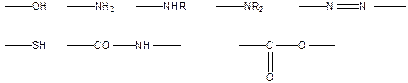Как построить изотерму поверхностного натяжения
Работа адсорбции



Наряду с поверхностной активностью для характеристики ПАВ используют еще один термодинамический параметр – работу адсорбции.
Работа адсорбции ( 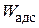
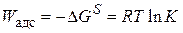
где 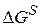
Рассчитаем разность работ адсорбции для двух соседних членов гомологического ряда:
Таким образом, для перевода каждой –СН2-группы из поверхностного слоя в объемную фазу надо затратить около 3 кДж/моль. Это работа раздвижения дипольных молекул воды (на величину –СН2-группы). Так как размер группы –СН2– один и тот же, то работа адсорбции одна и та же. Следовательно, носителем поверхностной активности ПАВ является углеводородный радикал.
3.3.6. Расчет гиббсовской адсорбции из изотермы
поверхностного натяжения методом графического
дифференцирования
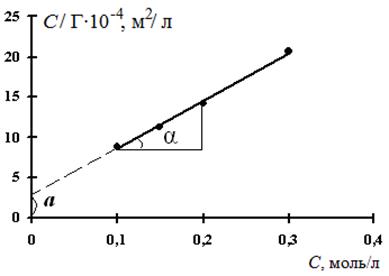
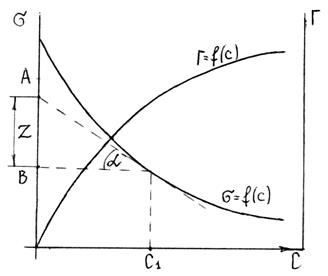
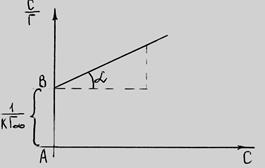
Зная зависимость поверхностного натяжения раствора от концентрации растворенного вещества, можно рассчитать изотерму адсорбции ПАВ методом графического дифференцирования экспериментальной кривой σ = f(C). Для этого в нескольких точках кривой σ = f(C) проводят касательные и определяют тангенсы угла их наклона, которые соответствуют значениям производных dσ / dС в этих точках (рис. 3.28). Зная значения этих производных, по уравнению адсорбции Гиббса рассчитывают величины Г, что позволяет построить изотерму адсорбции Г = f(C).
Из рис. 3.28 видно, что:
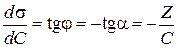
Подставим полученное значение в уравнение Гиббса (3.39):
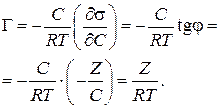
Таким способом рассчитывают величины адсорбции Г для ряда точек на кривой и по рассчитанным данным строят изотерму адсорбции в координатах Г = f(C), (рис. 3.29).
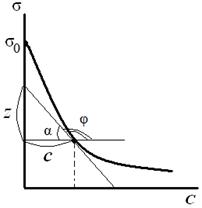 | 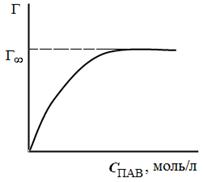 |
| Рис. 3.28. Графическое дифференцирование изотермы поверхностного натяжения | Рис. 3.29. Изотерма адсорбции в координатах Г = f(C) |
3.3.7. Применение уравнения изотермы Лэнгмюра
к адсорбции на границе жидкость–газ.
Расчет молекулярных характеристик исследуемого ПАВ
Уравнение изотермы мономолекулярной адсорбции Лэнгмюра для адсорбции на границе жидкость – газ (3.34) позволяет определить молекулярные характеристики ПАВ в поверхностном слое. Для этого:
1. Уравнение Лэнгмюра приводят к линейному виду:
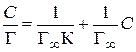
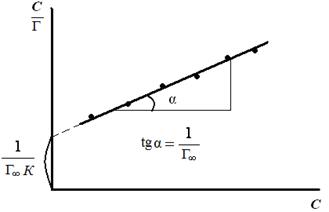
2. Строят изотерму адсорбции в координатах линейной формы уравнения Лэнгмюра (рис. 3.30).
Рис. 3.30. Изотерма адсорбции
в координатах линейной формы уравнения Лэнгмюра
3. Определяют емкость адсорбционного монослоя как котангенс угла наклона прямой линии:
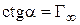
4. Зная значение 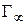
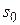
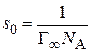
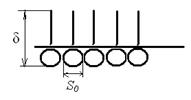
а также длину молекулы ПАВ (δ):
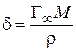
где 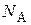
ρ– плотность ПАВ.
Рис. 3.31. Молекулярные характеристики ПАВ
Пример 3.5.При исследовании поверхностной активности растворов уксусной кислоты при 20 °С были получены следующие данные:
Найдите площадь, занимаемую одной молекулой кислоты и толщину адсорбционного слоя (длину молекулы).
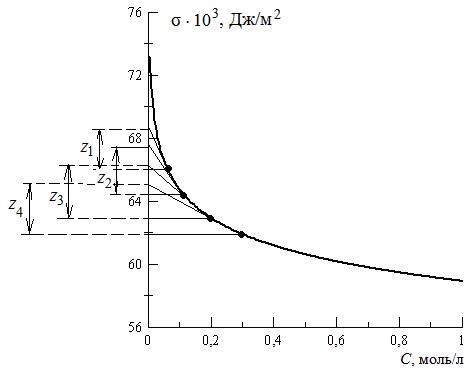
1. По экспериментальным данным строим изотерму поверхностного натяжения и проводим ее графическое дифференцирование. Для этого из нескольких точек кривой σ = f(C) проводим касательные до пересечения их с осью ординат и прямые, параллельные оси абсцисс. Получим отрезок Z, отсекаемый на оси ординат проведенными линиями.
2. Полученные значения Z при различных значениях С занесем в таблицу. Заполнение таблицы продолжим после проведения дальнейших расчетов.
Рис. 3.32. Графическое дифференцирование
изотермы поверхностного натяжения
3. Вычислим значение величины адсорбции Г по уравнению (3.39) для С = 0,1 моль/л:
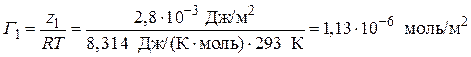
Аналогичный расчет проведем для других концентраций. Полученные результаты занесем в таблицу.
4. По полученным результатам расчетов, приведенных в таблице, строим изотерму адсорбции Лэнгмюра в координатахГ = f(C).
5. Рассчитываем значения 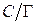
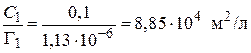
Аналогичный расчет проведем для других значений С. Полученные результаты занесем в таблицу.
6. Для нахождения величины предельной адсорбции Г∞ строим изотерму адсорбции в координатах линейной формы уравнении Лэнгмюра 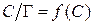
7. Экстраполяция прямой до оси ординат дает отрезок, равный 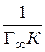
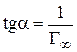
Рис. 3.33. Изотерма адсорбции
в координатах линейной формы уравнения Лэнгмюра
8. Рассчитываем константы уравнения Лэнгмюра:
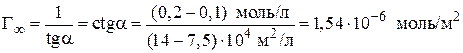
9. Зная величину 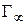
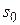
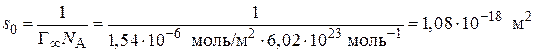
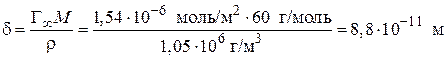
Пример 3.6.При 293 К зависимость поверхностного натяжения от концентрации водного раствора пропилового спирта выражается уравнением Шишковского: 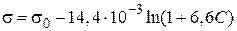
Подставим константы уравнения Шишковского в уравнение (3.42):
1. Вычислим величину предельной адсорбции:
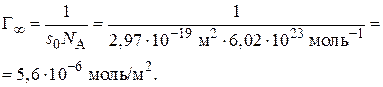
2. Вычислим величину постоянной В в уравнении Шишковского:
Построение изотермы поверхностного натяжения и адсорбции олеата натрия.
Цель работы:измерить поверхностное натяжение серии растворов ПАВ методом наибольшего давления газового пузырька; рассчитать поверхностное натяжение растворов, построить изотерму поверхностного натяжения, рассчитать площадь поперечного сечения S0 и длину молекулы ПАВ – ℓ.
Методика проведения эксперимента:
Измерение поверхностного натяжения проводят по методу наибольшего давления газового пузырька, разработанного П.А. Ребиндером.
Из полученного у преподавателя раствора поверхностно-активного вещества готовят методом разбавления серию растворов известной концентрации.
Измерение поверхностного натяжения приготовленных растворов начинают с установки капилляра прибора. Для этого в сосуд с отростком (предварительно тщательно вымытый хромовой смесью) наливают дистиллированную воду и плотно с помощью резиновой пробки вставляют капилляр таким образом, чтобы его нижний конец едва касался поверхности воды. Открывая кран аспиратора, создают разряжение в измерительном сосуде за счёт вытекания из аспиратора воды. Замечают появление у конца капилляра пробулькивающих пузырьков воздуха и регулируют скорость вытекания воды таким образом, чтобы время между проскоками отдельных пузырьков лежало в пределах 5-10 сек.
После этого замеряют ряд максимальных положений столба окрашенной жидкости в одном колене манометра и ряд минимальных положений в другом. Разница между средними значениями этих отсчётов даёт величину максимального перепада давлений. По найденной разнице h2 – h1 находят постоянную капилляра по формуле:

Аналогичным образом производится измерение D h для каждого из пяти приготовленных растворов ПАВ. Измерение начинают с самого разбавленного раствора и заканчивают исходным раствором, чтобы избежать излишнего загрязнения ячейки и облегчить её отмывку после каждого измерения.
Необходимо обратить внимание на «чистоту» проведения эксперимента, так как попадание посторонних примесей может исказить результаты.
По найденным значениям Dh для каждого из пяти растворов ПАВ вычисляется поверхностное натяжение по формуле: s = К´Dh.


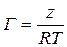
По рассчитанным значениям адсорбции (Г) строят изотерму адсорбции и, экстраполируя полученную кривую, находят значение Гмах. (участок изотермы, параллельный оси абсцисс).
Зная значение Гмах., рассчитывают площадь поперечного сечения S0 и длину 1 молекул ПАВ.
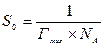
2. Молекулы, каких веществ могут обладать поверхностной активностью?
3. Изобразите схематично ориентацию молекул олеата натрия на границе раздела вода/воздух.
4. Какими еще методами можно определить величину поверхностного натяжения олеата натри,я кроме использованного?
ЗАНЯТИЕ 2.1.2.
ТЕМА:Адсорбция на границе раздела: твёрдое тело-газ, твёрдое тело-жидкость.
ЦЕЛЬ ЗАНЯТИЯ:изучив теоретические закономерности адсорбции веществ на твёрдых адсорбентах, научиться экспериментально определять величину адсорбции на твёрдом адсорбенте.
ЗНАЧЕНИЕ ИЗУЧАЕМОЙ ТЕМЫ:адсорбция лекарственных веществ является одной из стадий их метаболизма. В результате адсорбции концентрация лекарственных веществ может быть увеличена на порядок и более, что в соответствии с законами кинетики увеличивает скорость биохимических реакций, особенно ферментативных.
Адсорбенты часто используются в рецептуре аптек. Адсорбционные явления могут служить причиной несовместимости в лекарственных формах, чаще всего в порошках, микстурах, взвесях.
Адсорбентами, как правило, являются высокодисперсные вещества, нерастворимые и не всасывающиеся в организме человека (уголь, гидроксид алюминия, белая глина, растительные порошки), которые значительно снижают терапевтическую активность лекарств при одновременном их применении с алкалоидами, гликозидами и др. веществами.
1. Измерение величины адсорбции на границах раздела: твёрдое тело-газ и твёрдое тело-раствор.
2. Факторы, влияющие на величину адсорбции газов и растворённых веществ.
3. Уравнение изотермы адсорбции Лэнгмюра. Основные положения теории мономолекулярной адсорбции Лэнгмюра. Изотерма мономолекулярной адсорбции.
4. Уравнение адсорбции Фрейндлиха. Изотерма адсорбции Фрейндлиха. Применимость уравнения Фрейндлиха.
5. Капиллярная конденсация.
6. Применение адсорбции на границе твёрдое тело-газ, твёрдое тело-раствор для очистки лекарственных веществ, для извлечения действующих веществ из лекарственного сырья.
Лабораторная работа:
«Построение изотермы адсорбции йода на активированном угле».
(для построения графика необходима миллиметровая бумага).
Обучающие задачи.
Задача 1.Полистирольный сульфокатионит в Н + форме в количестве 1г внесли в раствор КС1 с концентрацией 100 моль/м 3 объёмом 50 мл и смесь выдержали до равновесного состояния. Константа адсорбционного равновесия К = 2,5. Полная обменная ёмкость катионита 5 моль/кг. Определить равновесную концентрацию ионов калия в ионите.
Решение: Количество адсорбируемого вещества (К + ) можно определить из уравнения Лэнгмюра и из уравнения Фрейндлиха:
Обозначим равновесную концентрацию ионов калия в растворе через x и составим уравнение:
(корень не действителен) Сравн.=0,08 моль/л.
Задача 2.Определить константы в уравнении изотермы адсорбции Лэнгмюра для растворов гексанола на основании следующих экспериментальных данных:
Решение: для нахождения констант преобразуем уравнение Лэнгмюра в уравнение прямой:
Задача 3:На основании экспериментальных данных, полученных при изучении адсорбции бензойной кислоты углем из её раствора в бензоле при 25 0 С, определить графически константы b и n в уравнении Фрейндлиха.
| С, моль/л | 0,006 | 0,025 | 0,053 | 0,118 |
| х /m, ммоль/г | 0,44 | 0,78 | 1,04 | 1,44 |
Решение: для определения коэффициентов в уравнении Фрейндлиха преобразуем его в уравнение прямой линии: 1g х /m = 1g b + 1/n 1g С; Для построения прямой находим 1g С и 1g х/m:
Отрезок, отсекаемый прямой на оси ординат равен 1g b, а тангенс угла наклона – 1/n.
1g b = 0,5; b = 3,16; tg a = 0,31; 1/n = 0,31; n = 3,2.
Задачи для самостоятельного решения.
Задача 1. При изучении адсорбции ацетона древесным активированным углем при 20 0 С были получены следующие результаты:
| концентрация ацетона в растворе, ммоль/л | 2,34 | 14,65 | 88,62 | 177,69 | 268,97 |
| количество адсорбированного ацетона 1 г угля, ммоль/г | 0,208 | 0,618 | 1,50 | 2,08 | 2,88 |
Определить графически постоянные b и n в уравнении изотермы адсорбции Фрейдлиха и рассчитать количество ацетона, адсорбируемое 1г угля при равновесной концентрации ацетона 125 ммоль/л.
Определить равновесную концентрацию хлорид-ионов в ионите и величину адсорбции.
Задача 3.Вычислить равновесную концентрацию уксусного альдегида, если 10 г активированного древесного угля адсорбирует 25,7 ммоль уксусного альдегида. Константы в уравнении Фрейдлиха: b = 14,2; n = 1,75.
Лабораторная работа №2.
Построение изотермы адсорбции йода на активированном угле.
Цель работы:определить значения адсорбции йода из растворов различной концентрации на активированном угле, построить изотерму адсорбции и графически определить константы уравнения Фрейндлиха.
Построение изотермы адсорбции и нахождение величин
Изотерма адсорбции описывается уравнением Ленгмюра:
где 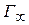
ванного на 1 м 2 поверхности, кмоль/м 2 ;
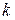
Зная Г можно рассчитать площадь S, приходящуюся на 1 молекулу.
Число адсорбированных молекул на 1 м 2 составляет:
С увеличением Г величина S уменьшается и при 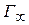
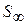
Пользуясь 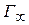
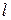
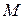
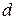
Строят изотерму ПН (зависимость 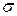
По изотерме ПН рассчитывают Г по уравнению Гиббса.
Для этого к кривой 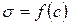
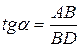
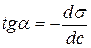
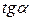
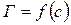
Рис. 6.5. Построение изотермы адсорбции по изотерме
Каждой концентрации С соответствует отрезок Z на оси ординат.
Длина отрезка, выраженная в единицах ПН равна: 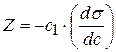
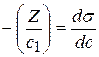
Подставив полученные значения Z в уравнение:
Используя Z для ряда концентраций, рассчитывают адсорбцию Г.
Строят изотерму адсорбции, откладывая по оси абсцисс С, а по оси ординат Г.
Где сложно провести касательную (в интервале концентраций 0,2-0,15 моль/л) рассчитывают изменение: 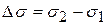
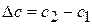
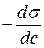
Данные заносят в таблицу:
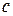 | 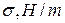 | 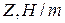 | 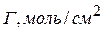 | 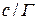 |
Значение 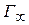
Рис. 6.6. График уравнения Ленгмюра в прямолинейных координатах.
Угол 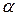
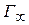
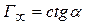
Отрезок 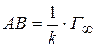
Из этого уравнения определяем 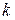
Из уравнения 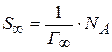
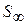

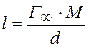
Лекция 7.Поверхностные явления. Адсорбция
Изотерма адсорбции. Причины адсорбции.
Частные случаи адсорбции.
Одним из основных поверхностных явлений в коллоидных системах, обладающих поверхностью, является адсорбция. С адсорбцией связаны коагуляция, пептизация, изменение знака заряда частиц и другие явления.
Адсорбцией называется концентрирование газообразного или растворенного вещества на поверхности раздела фаз.
Различают понятия: сорбция, адсорбция, абсорбция.
Вещество, которое адсорбируется, называется адсорбтивом или адсорбатом.
Для определения адсорбции необходимо найти экспериментально давление газа или количество адсорбтива в объеме, в котором происходит адсорбция, до и после адсорбции. Чаще всего адсорбцию определяют по привесу адсорбента.
Общую термодинамическую теорию адсорбции разработал в конце XIX века Гиббс. В XX веке адсорбцию исследовали: Лэнгмюр, Поляни, Брунауэр, Гурович, Шилов, Дубинин и др.
Различают адсорбцию физическую и химическую.
Физическая адсорбция обеспечивается силами Ван-дер-Ваальса, протекает самопроизвольно, молекулы адсорбтива могут перемещаться по поверхности (нелокализованная адсорбция), характеризуется обратимостью, отсутствием стехиометрических соотношений, уменьшением адсорбции при повышении температуры, сопровождается десорбцией. Процессы адсорбции и десорбции находятся в равновесии: адсорбция « десорбция.
Химическая адсорбция или хемосорбция обусловлена химическим взаимодействием адсорбента с адсорбтивом. Молекулы адсорбтива не могут перемещаться по поверхности адсорбента. Необратима. Тепловой эффект близок к энергии образования химических соединений. Повышение температуры способствует хемосорбции.
Адсорбцию чаще всего характеризуют зависимостью количества адсорбируемого вещества а от концентрации или давления 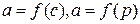
На изотерме можно выделить три участка:
Изотерма адсорбции по виду напоминает параболу.
|  |
Рис. 7.1. Изотермы адсорбции.
Для аналитического выражения изотермы, Фрейндлих предложил эмпирическое уравнение вида:
где 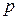
Для сорбции твердого вещества из раствора:
Физический смысл константы К становится ясным, если принять с=1. Тогда К представляет собой величину адсорбции при равновесной концентрации адсорбтива, равной 1 моль/л.
Адсорбция обусловлена разными причинами.
Физическая сорбция осуществляется за счет сил Ван-дер-Ваальса между электронейтральными молекулами (1-10 кДж/моль).
Различают полярные и неполярные силы Ван-дер-Ваальса, проявление которых зависит от полярности молекул. Полярные силы делят на электростатические и индукционные.
К электростатическим относят силы, возникающие между молекулами, имеющими постоянный дипольный момент.
Индукционные силы также имеют электростатическую природу, но возникают между молекулой, имеющей постоянный дипольный момент, и неполярной молекулой, в которой индуцируется дипольный момент под действием первой полярной молекулы.
Неполярные (дисперсионные) силы возникают между неполярными молекулами и имеют сложную квантовомеханическую природу. Происхождение этих сил следующее: в неполярной молекуле можно выделить один электрон и рассмотреть его движение относительно ядер. Вследствие того, что электрон движется на некотором расстоянии от ядер, в молекуле в каждый момент времени возникает диполь, индуцирующий диполь в соседней молекуле.
Все виды Ван-дер-Ваальсового взаимодействия убывают пропорционально расстоянию между молекулами в шестой степени, т.е. для них характерен закон » 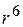
Чаще всего возникают все виды Ван-дер-Ваальсового взаимодействия одновременно, но с разной долей участия каждого вида. Вклад каждого из взаимодействий оценить сложно. Но качественно можно оценить виды сорбционного взаимодействия, зная строение адсорбента и адсорбтива.
Причиной адсорбции, близкой к физической, может быть также образование водородной связи. Атом водорода имеет значительно меньшие размеры, чем другие атомы и поэтому его ядро может подходить особенно близко к неподеленным парам электронов других атомов.
С этим связаны два важных свойства атома водорода.
Первое свойство заключается в большой подвижности водорода связанного с электроотрицательными атомами, имеющими неподеленную пару электронов (группа азота, кислорода, фтора). Связанный с этими атомами водород очень мало экранирован и к нему близко может подойти другой электроотрицательный атом, имеющий активную неподеленную пару электронов. Энергия электростатического притяжения между ними оказывается соизмеримой с энергией прежней связи.
Второе свойство заключается в том, что при сближении двух молекул до расстояния, допускающего переход протона, последний притягивается к обеим атомам и удерживает один ковалентной, а другой водородной связью, причем, между ними может происходить перемещение по схеме:
Вследствие этого, водородную связь рассматривают как донорно-акцепторную или как промежуточный тип связи между химической и физической связями.
Водородную связь обеспечивают группы:
В качестве донора электронов может выступать p-электронное облако двойных алифатических связей >С=С
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет