Как построить график sinx cosx

Урок по алгебре и началам анализа в 10-м классе с применением информационных технологий на тему «Тригонометрические функции. Функции y=sin x*y=cosx»

Разделы: Математика

1. Новый материал

Рассмотрим единичную окружность. Углы поворота существуют положительные и отрицательные.

Напомним, что поворотом плоскости вокруг точки О на угол называют такое геометрическое преобразование, при котором:

а) точка О отображается на себя;

б) каждый луч OX отображается на луч OX, такой, что угол XOX₁=и OX=OX₁.

Пусть точка Р₂ единичной окружности получена при повороте точки Р₀(1;0) на угол в радиан. Нетрудно понять, что ордината точки Р₂ – это синус угла , а абсцисса этой точки – косинус угла .

Т.к. повороты Р₂ и Р совпадают, то точка Р₂ будет соответствовать не только числу , но и всем числам вида , где nZ.

Пример: Дана точка Р₀(1;0). На единичной окружности постройте образцы точки Р₀ при поворотах плоскости вокруг начала координат на углы величиной

И запишите их координаты.

График функции y=sinx.

Вспомним изученные свойства функции y=sinx.

Вариант 1.

1. Найти градусную меру угла, выраженного в радианах:

,

2. Найти координаты точки, полученной поворотом точки Р(1;0) на угол:

а) Z

б) Z

3. Найти все углы (в радианах), на которые нужно повернуть точку Р(1;0), чтобы получить точку с координатами:

а) cos

б) 2sin(-

5. Упростить выражение:

а)

б)

Вариант 2.

1. Найти градусную меру угла, выраженного в радианах:

2. Найти координаты точки, полученной поворотом точки Р(1;0) на угол:

а) Z

б) kZ

3. Найти все углы (в радианах), на которые нужно повернуть точку Р(1;0), чтобы получить точку с координатами:

а) sin

б) cos(-)*3tg(-

5. Упростить выражение:

а)

б)

Подведение итогов урока:

На доска интерактивная таблица с результатами урока.

Подготовить компьютерную презентацию на тему: “Движения графиков тригонометрических функций”

Источник

14. Свойства функций синуса, косинуса, тангенса

и котангенса и их графики

14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК

График функции y = sin x (синусоида)

Свойства функции y = sin x

Объяснение и обоснование

Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:

1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями

координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее

З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох

(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.

Напомним, что значение синуса — это ордина-

та соответствующей точки единичной окружности

(рис. 79). Поскольку ординату можно найти для

любой точки единичной окружности (в силу того,

что через любую точку окружности всегда можно

провести единственную прямую, перпендикуляр-

ную оси ординат), то область определения функции

y = sin x — все действительные числа. Это можно за-

писать так: D (sin x) = R.

Для точек единичной окружности ординаты нахо-

дятся в промежутке [–1; 1] и принимают все значения

от –1 до 1, поскольку через любую точку отрезка [–1; 1]

оси ординат (который является диаметром единичной

окружности) всегда можно провести прямую, перпендикулярную оси орди-

нат, и получить точку окружности, которая имеет рассматриваемую орди-

нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].

Это можно записать так: E (sin x) = [–1; 1].

Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окружности является точка A, то есть при

Наименьшее значение функции sin x равно минус единице. Это значение

достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть

при

поэтому ее график симметричен относительно начала координат.

В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом

k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых sin x, то есть ордината соответствующей точки единичной окруж­

ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-

ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).

функции синус положительны (то есть ордината соответствующей точки

единичной окружности положительна) в I и II четвертях (рис. 80). Таким

образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех

x ∈ (2πk; π + 2πk), k ∈ Z.

Значения функции синус отрицательны (то есть ордината соответствую-

щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-

Промежутки возрастания и убывания

Учитывая периодичность функции sin x с периодом T = 2π, достаточно

исследовать ее на возрастание и убывание на любом промежутке длиной

2π, например на промежутке

то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной окружности увеличивается (то есть

sin x ₂ > sin x ₁ ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,

делаем вывод, что она такж е возрастает на каждом из промежутков

Если x ∈ (рис. 81, б), то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной

окружности уменьшается (то есть sin x _{2 1} ), таким образом, на этом промежутке функция sin x убывает. Учитывая

периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой

функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на

промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината

соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на

промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для

построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат

Поскольку мы построили график на

промежутке длиной 2π, то, учитывая

периодичность синуса (с периодом 2π),

повторяем вид графика на каждом про-

межутке длиной 2π (то есть переносим па-

раллельно график вдоль оси Ох на 2πk,

где k — целое число).

Получаем график, который называется

З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,

множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,

описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими

колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль

координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией

времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная

фаза,

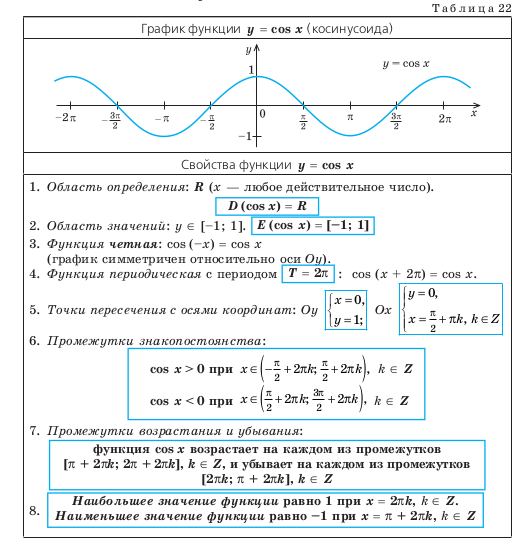
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК

Объяснение и обоснование

Напомним, что значение косинуса — это абсцис-

са соответствующей точки единичной окружности

(рис. 85). Поскольку абсциссу можно найти для лю-

бой точки единичной окружности (в силу того, что

через любую точку окружности, всегда можно про-

вести единственную прямую, перпендикулярную оси

абсцисс), то область определения функции y = cos x —

все действительные числа. Это можно записать так:

D (cos x) = R.

Для точек единичной окружности абсциссы нахо-

дятся в промежутке [–1; 1] и принимают все значе-

ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной

всегда можно провести прямую, перпендикулярную оси абсцисс, и получить

точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:

y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это

зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при

x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.

Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси

Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом

T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.

соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только

тогда, когда на единичной окружности будут выбраны точки C или D, то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции косинус положительны (то есть абсцисса соответствующей точки

единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-

тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех

Значения функции косинус отрицательны (то есть абсцисса соответству-

ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,

поэтому cos x

Промежутки возрастания и убывания

Учитывая периодичность функции cos x (T = 2π), достаточно исследовать

ее на возрастание и убывание на любом промежутке длиной 2π, например

на промежутке [0; 2π].

Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x ₂ > x ₁ ) абсцисса соответствующей точки единичной

окружности уменьшается (то есть cos x _{2 1} ), следовательно, на этом промежутке функция cos x убывает. Учитывая

периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.

Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x ₂ > x ₁ ) аб-

сцисса соответствующей точки единичной окружности увеличивается (то

есть cos x ₂ >cos x ₁ ), таким образом, на этом промежутке функция cos x

возрастает. Учитывая периодичность функции cos x, делаем вывод, что

она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.

Проведенное исследование позволяет построить график функции y = cos x

аналогично тому, как был построен график функ-

ции y = sin x. Но график функции у = cos x можно

также получить с помощью геометрических преоб-

разований графика функции у = sin х, используя

Эту формулу можно обосновать, например, так.

Рассмотрим единичную окружность (рис. 88), отметим на ней точки

Источник

Презентация по математике на тему: «Тригонометрические функции вида y=sinx, y=cosx».

Описание презентации по отдельным слайдам:

Тригонометрические функции вида: y=cosx и y=sinx, и их свойства ГБПОУ КДПИ им. К Фаберже Преподаватель математики Костенкова С.С. 2016 2016 г.

Основные свойства 1. область определения, 2. область значения, 3. периодичность функции. 4. четность или нечетность, 5. монотонность, 6. ограниченность, 7. непрерывность, 8. наибольшее и наименьшее значение.

7. Функция определена и непрерывна на всем множестве действительных чисел. 8.Принимает наибольшее значение равное 1, в точке x= π/2 +2πk, kϵZ Принимает наименьшее значение равное −1, в точке x= 3π/2 +2πk, kϵZ

4. Функция у = cosx является четной т.к. выполняется равенство cos(- x) = cos(x) (график функции симметричен относительно оси ординат). 5. Монотонность. На отрезке [ −π +2πn; 2πn] функция y = cosx возрастает, а убывает на отрезке [2πn ; π +2πn ], nϵZ 6. Функция у = cosx является ограниченной, т.к. для любого x верно неравенство – 1 ≤ cos x ≤ 1.

Построение графиков y=cosx, y=sinx

Алгоритм построения графиков функций Алгоритм построения графика функции y = cos2x: 1. Построить график y = cosx 2. Сжать в 2 раза по оси ОХ Алгоритм построения графика функции y = cos1/2x: 1. Построить график y = cosx 2. Растянуть в 2 раза по оси ОХ

Пример 1. Построить график функции у = sin 2x. Решение. k = 2; График функции у = f (kx) получается из графика функции у = f (x) с помощью сжатия к оси у с коэффициентом k.

Алгоритм построения графиков функций Алгоритм построения графика функции y = 2cosx: 1. Построить график y = cosx 2. Увеличить ординату в 2 раза Алгоритм построения графика функции y = 1/2cosx: 1. Построить график y = cosx 2. Уменьшить ординату в 2 раза.

Алгоритм построения графиков функций Алгоритм построения графика функции y = sin(x + 2): 1. Построить график y = sinx. 2. Сдвинуть график на 2 единицы влево по оси ОХ. Алгоритм построения графика функции y = sin(x – 2): 1. Построить график y = sinx. 2. Сдвинуть график на 2 единицы вправо по оси ОХ.

Алгоритм построения графиков функций Алгоритм построения графика функции y = sinx + 2: 1. Построить график y = sinx. 2. Сдвинуть график на 2 единицы вверх по оси Оy Алгоритм построения графика функции y = sinx – 2: 1. Построить график y = sinx. 2. Сдвинуть график на 2 единицы вниз по оси Оy

Алгоритм построения графиков функций Построить график y = – cosx: 1. Построить график y = cosx 2. Выполнить зеркальное отображение относительно оси ОХ.

Домашнее задание Построить графики функций y = cos(x + 2) y = sinx + 2 y = 1/3sinx y = 4 – cosx y = sin(x – 5) y = – 3cosx

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-351906

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минздрав включил вакцинацию подростков от ковида в календарь прививок

Время чтения: 1 минута

В российских школах могут появиться «службы примирения»

Время чтения: 1 минута

Костромская область разработала программу привлечения педагогических кадров

Время чтения: 2 минуты

Чем заняться с детьми в новогодние праздники в Москве

Время чтения: 4 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Немного теории.

Тригонометрические уравнения

Уравнение cos(х) = а

Уравнение cos x = а, где \( |a| \leqslant 1 \), имеет на отрезке \( 0 \leqslant x \leqslant \pi \) только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если a

Уравнение sin(х) = а

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Уравнения, сводящиеся к квадратным

Уравнение вида a sin(x) + b cos(x) = c

Используя формулы \( \sin(x) = 2\sin\frac <2>\cos\frac<2>, \; \cos(x) = \cos^2 \frac <2>-\sin^2 \frac <2>\) и записывая правую часть уравпения в виде \( 2 = 2 \cdot 1 = 2 \left( \sin^2 \frac <2>+ \cos^2 \frac <2>\right) \) получаем

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях \( a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 \) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на \( \sqrt \):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, \( \sqrt = 5 \). Поделим обе части уравнения на 5:

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Источник