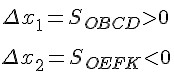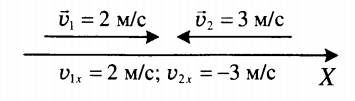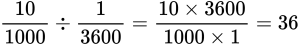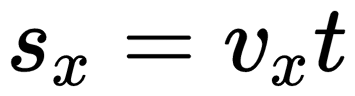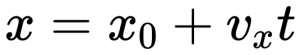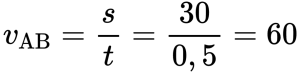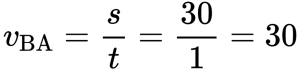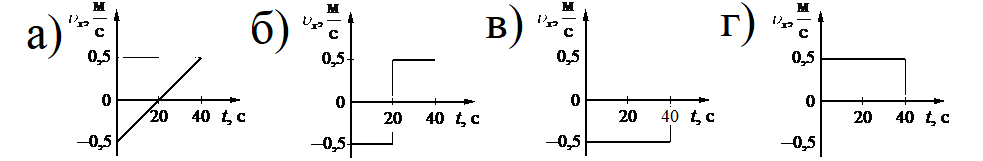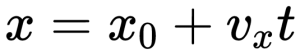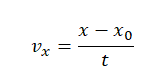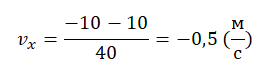Как построить график модуля скорости

Как построить график модуля скорости

§ 15. Графики зависимости модуля и проекции скорости равномерного прямолинейного движения от времени

1. График модуля скорости.

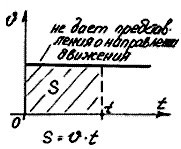
Зная график модуля скорости, можно найти не только модуль скорости, но и путь S, пройденный точкой. Он численно равен площади прямоугольника, расположенного под графиком модуля скорости.

2. Графики проекции скорости.

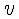
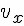
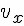
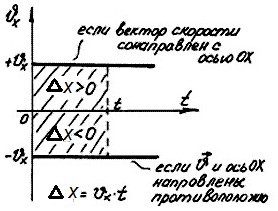
Так как = const, то и = const. Поэтому графиками также будут прямые линии, параллельные оси времени. Но в отличие от модуля проекции могут быть как положительными, так и отрицательными. Поэтому графиком = f (t) является прямая, параллельная оси времени, которая может быть расположена как выше, так и ниже оси t.

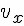
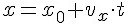
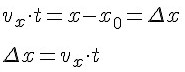
По графикам можно найти проекцию и модуль скорости. По знаку проекции скорости можно судить о направлении движения точки относительно оси OX. Если > 0, то вектор скорости точки сонаправлен с осью OX, и точка движется в положительном направлении оси. Если же

.

.

Изменение координаты движущейся точки численно равно площади прямоугольника между графиком проекции скорости и осью времени. Площади приписывают знак «плюс» или «минус». Если график расположен выше оси времени, то площадь считают положительной, и изменение координаты движущейся точки больше нуля. Если график расположен ниже оси времени, то площадь считают отрицательной, и изменение координаты движущейся точки меньше нуля.

Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.

Источник

§ 1.6. График скорости равномерного прямолинейного движения. График пути. график координаты

Познакомимся подробнее с самым наглядным способом описания движения — графическим — на примере равномерного прямолинейного движения.

График модуля скорости

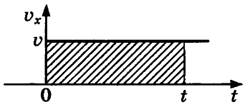
При равномерном прямолинейном движении скорость v_x = const. Следовательно, и ее модуль v = const, т. е. не изменяется с течением времени. Графиком зависимости модуля скорости от времени 1 является прямая АВ, параллельная оси времени и расположенная выше этой оси, так как v > О (рис. 1.9).

Площадь прямоугольника ОАВС, заштрихованного на рисунке, численно равна пути, пройденному телом за время t. Ведь сторона ОА в определенном масштабе есть модуль скорости v, а сторона ОС — время движения t, поэтому s = vt.

График скорости

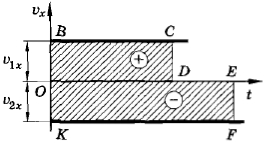
В отличие от модуля скорости скорость, определяемая выражением (1.4.1), может быть положительной или отрицательной. Поэтому графиком зависимости скорости v_x от времени t может быть либо прямая ВС, либо прямая KF (рис. 1.10).

Обе прямые параллельны оси времени. Прямая ВС соответствует положительному значению скорости (v_1x > 0), а прямая KF — отрицательному значению (v_2x О, то изменение координаты первого тела Аx₁ = v_1xt₁ положительно. Поэтому и площади прямоугольника OBCD приписывается положительный знак. Скорость движения второго тела отрицательна: v_2x 0; прямая 2 — случаю, когда х₀₂ 0; а прямая 3 — случаю, когда х₀₃ > 0, v_3x

Обратите внимание на то, что по графику зависимости x(t) можно судить о «прошлом» в движении тела, т. е. можно находить положения тела до начала отсчета времени при условии, что и до этого момента тело двигалось равномерно и прямолинейно с той же скоростью. Моменты времени до начала отсчета считаются отрицательными. Согласно рисунку 1.13 за 3 с до начала отсчета времени тело имело координату 4,5 м.

Все графики равномерного прямолинейного движения представляют собой прямые линии. Для их построения достаточно указать значения x(t) или s(t) для двух моментов времени.

1 В дальнейшем для краткости мы будем часто говорить: «график модуля скорости», «график проекции скорости» и т. д.

Источник

График зависимости модуля скорости от времени

при прямолинейном равноускоренном движении график зависимости модуля скорости от времени — отрезок прямой.

Чтобы построить такой график, достаточно найти две принадлежащие ему точки и провести через них отрезок прямой.

Рассмотрим на примерах, как построить график зависимости модуля скорости от времени и какую информацию о движении тела можно получить, изучая такой график.

1. Построим график зависимости от времени модуля скорости свободно падающего тела, если: а) начальная скорость тела равна нулю; б) начальная скорость тела направлена вниз и

Решение. Найдем по две точки для каждого графика — соответствующую начальному моменту времени и соответствующую моменту времени t = 1с.

В случае а) зависимость модуля скорости от времени выражается формулой υ = gt, поэтому при t = 0 с скорость тела равна нулю, а при t = 1с скорость тела равна (Соответствующие точки графика обозначены красным на рис. 3.4.)

В случае б) зависимость модуля скорости от времени выражается формулой υ = υ₀ + gt, где Поэтому при t = 0 с скорость тела равна а при t = 1с скорость тела ответствующие точки графика обозначены зеленым на рис. 3.4.)

Рис. 3.4. Графики зависимости модуля скорости от времени для прямолинейного равноускоренного движения: а — без начальной скорости; б — с начальной скоростью

Проводя через найденные точки отрезки прямых, получаем искомые графики (см. рис. 3.4).

Построенные графики оказались параллельными отрезками. Обусловлено это тем, что тела́ двигались с одинаковым ускорением.

Источник

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

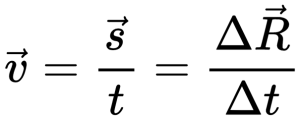
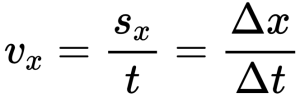
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Спидометр — прибор для измерения модули скорости тела.

График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

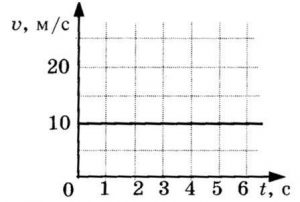
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

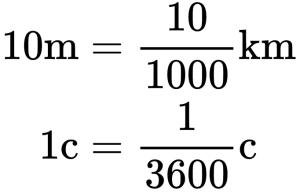
Перемещение и координаты тела при равномерном прямолинейном движении

Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

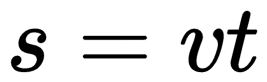
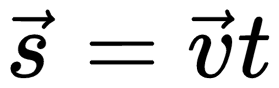
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

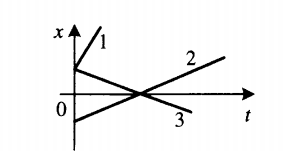
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид:

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

Пример №2. График зависимости координаты тела от времени имеет вид:

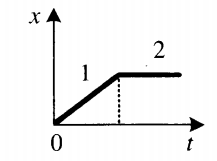
Изучите график и на его основании выберите два верных утверждения:

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

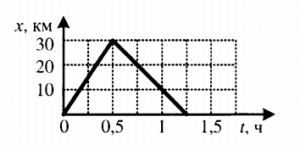
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Алгоритм решения

Уравнение координаты при равномерном прямолинейном движении имеет вид:

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Графики прямолинейного движения

Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.

Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.

Будем отдельно рассматривать:

1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: \(\vec =0\).

2). Неравномерное движение — скорость меняется и появляется ускорение.

Пусть ускорение есть и, оно не изменяется: \(\vec =const\). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:

Примечание: Когда изменяется скорость, всегда появляется ускорение!

Движение будем изображать графически, используя две перпендикулярные оси.

На графиках будем откладывать:

Для каждого вида движения получим три графика. Графики будем называть так:

Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.

Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют

Пусть тело покоится на оси Ox – (рис 1а).
Точкой \(x_<0>\) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
\[x=x_<0>\]

Скорость и ускорение неподвижного тела равны нулю:

Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.

Скорость не меняется — движение равномерное

Разберём равномерное движение в направлении оси (рис. 2а).

Начальная координата тела – это точка \(x_<0>\), а конечная координата — точка \(x\) на оси Ox. В точку «x» тело переместится к конечному времени «t».

Красной стрелкой обозначено направление, в котором тело движется.

Примечание: Тело движется туда, куда направлен вектор его скорости.

Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).

Уравнение, описывающее изменение координаты выглядят так:

Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:

Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:

Равномерное движение в направлении противоположном оси

Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).

Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.

Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.

Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.

А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.

Равноускоренное движение в направлении оси, скорость увеличивается

Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.

Уравнение, которое описывает квадратичное изменение координаты, выглядит так:

Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:

Ускорение есть (рис. 4г) и оно не меняется:

Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.

Примечания:

1). Координата «x» будет изменяться:

2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.

3). Квадратичный закон – это уравнение второй степени, на графике — парабола.

4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.

Равноускоренное движение против оси

Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).

Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).

Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов \(\vec\) и \(\vec\) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.

Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.

Скорость уменьшается — движение равнозамедленное

Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).

Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).

Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).

А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).

Равнозамедленное движение против оси

Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).

Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).

Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).

Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.

Выводы

2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).

3). Если скорость не меняется, ускорения нет.

4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.

5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.

Источник