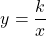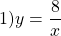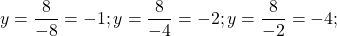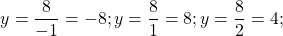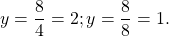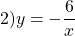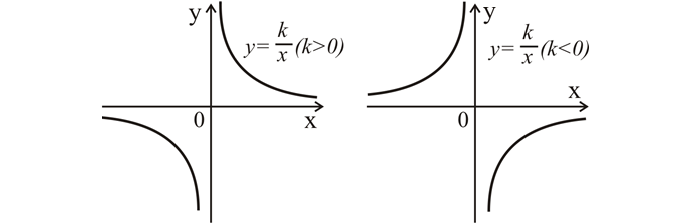Как построить график функции обратной пропорциональности
Обратная пропорциональность и её график
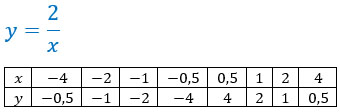
Рассмотрим функцию, которая задается формулой
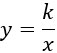
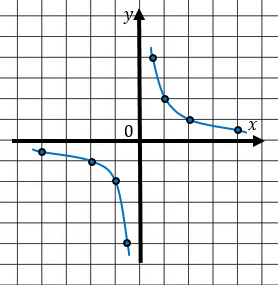
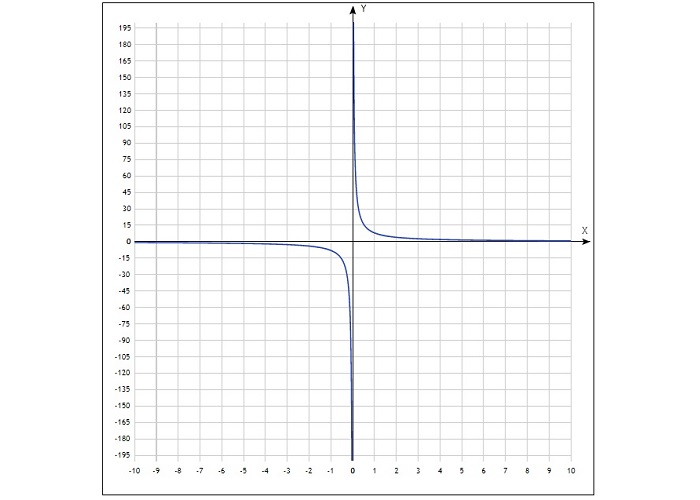
Такая функция называется обратной пропорциональностью, причем x ≠ 0 (т.к. на 0 делить нельзя). Число k также отлично от 0 (в противном случае функция перестанет являться обратной пропорциональностью). Её графиком является гипербола, состоящая из двух ветвей. Ты сможешь увидеть ее ниже.
Перед разбором тренировочных экзаменационных заданий очень хочется вспомнить, что конкретно влияет на расположение и вид графика.
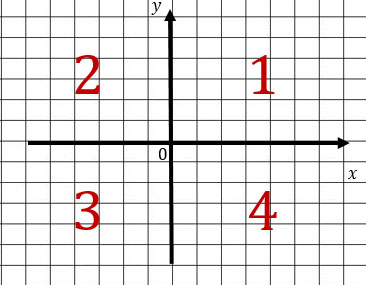
Напомню, что координатная плоскость делится на 4 координатных четверти. У каждой четверти есть свой порядковый номер (см. рисунок).
Так вот к чему я это?
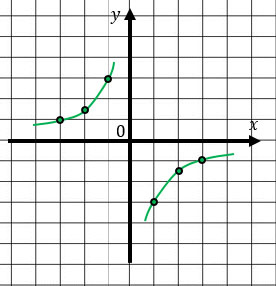
Если k > 0, то ветви гиперболы располагаются в 1 и 3 четвертях.
Если k < 0, то ветви гиперболы располагаются во 2 и 4 четвертях.
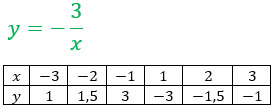
Убедимся в этом) Построим два графика.
Чем больше точек ты запишешь, тем точнее получится график.
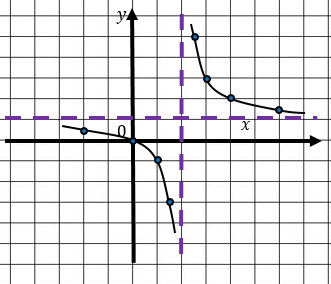
Но не всегда оси будут асимптотами.
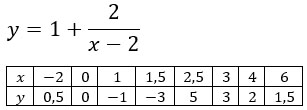
Например, в следующей функции асимптотами будут являться прямые х = 2 и у = 1.
Практикум по гиперболам.
Оказывается, что на сайте ФИПИ все задания чисто с гиперболами однотипные, поэтому разберу только два задания, похожих друг на друга (почему они оси не прорисовывают не пойму).
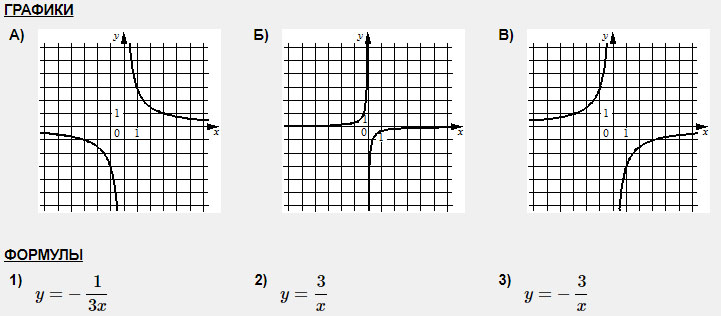
Задание 1. Установите соответствие между графиками и их функциями.
Из общей массы выделяется график Б, т.к. ветви этой гиперболы находятся очень близко к началу координат. А из формул выделяется формула 1, т.к. в ее знаменателе икс умножен на 3. Вывод: график Б и формула 1 созданы друг для друга!
Далее, ветви графика А расположены в 1 и 3 четвертях плоскости, значит коэффициент k положительный. К А подходит формула 2.
И остались график В и формула 3.
Задание 2. Установите соответствие между функциями и их графиками.
График обратной пропорциональности
График обратной пропорциональности — функции
— гипербола. При k>0 ветви гиперболы расположены в I и III координатных четвертях, при k
Рассмотрим построение графика обратной пропорциональности на конкретных примерах.
Таким образом, нашли 8 точек с координатами
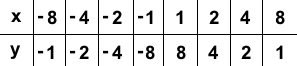
На практике эти вычисления оформляют в виде таблицы — в верхнюю строчку записывают выбранные значения x, в нижнюю — y, полученные при подстановке соответствующего значения x в формулу функции. Для функции y=8/x таблица выглядит так:

Полученные точки отмечаем на координатной плоскости:
Затем через эти точки проводим две ветви гиперболы:
Важно!
Оси Ox и Oy для гиперболы являются асимптотами. Это означает, что ветви гиперболы на бесконечности приближаются к осям, но никогда их не пересекут.
Для построения гиперболы можно брать только положительные значения x. Вторая ветвь гиперболы симметрична первой относительно точки O.
Эта функция — обратная пропорциональность. Её график — гипербола, ветви которой расположены во II и IV-й координатных четвертях. Для построения гиперболы составим таблицу:
Полученные точки отмечаем на координатной плоскости:
Обратная пропорциональность. Гипербола
Сейчас мы будем говорить об обратной пропорциональности, или другими словами об обратной зависимости, как о функции.
Мы закрепим понятие функции и научимся работать с коэффициентами и графиками.
А еще мы разберем несколько примеров построения графика функции — гиперболы.
Обратная пропорциональность — коротко о главном
Определение:
Функция, описывающая обратную пропорциональность, – это функция вида \( \displaystyle y=\frac
+b \), где \( k\ne 0\), \( x\ne 0\) и \( x\ne а\)
По-другому эту функцию называют обратной зависимостью.
Область определения и область значений функции:
График обратной пропорциональности (зависимости) – гипербола.
Коэффициент \( \displaystyle k\)
\( \displaystyle k\) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента \( \displaystyle k\) влияет на то, в каких четвертях расположен график:
если \( \displaystyle k>0\), то ветви гиперболы расположены в \( \displaystyle I\) и \( \displaystyle III\) четвертях;
если \( \displaystyle k
Коэффициент \( \displaystyle a\)
Если внимательно посмотреть на знаменатель, видим, что \( \displaystyle a\) – это такое число, которому не может равняться \( \displaystyle x\).
То есть \( x=a\) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции
Коэффициент \( b\)
Число \( b\) отвечает за смещение графика функции вверх на величину \( b\), если \( b>0\), и смещение вниз, если \( b
Пример 2
Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).
Напомню, что для этого надо найти корни соответствующего квадратного уравнения: \( \displaystyle <
Я найду их устно с помощью теоремы Виета: \( \displaystyle <
Итак, получаем: \( \displaystyle <
Пример 3
Ты уже попробовал решить сам? В чем загвоздка?
Наверняка в том, что в числителе у нас \( \displaystyle 2x\), а в знаменателе – просто \( \displaystyle x\).
Это не беда. Нам нужно будет сократить на \( \displaystyle \left( x+2 \right)\), поэтому в числителе следует вынести \( \displaystyle 2\) за скобки (чтобы в скобках \( \displaystyle x\) получился уже без коэффициента):
Ответ: \( \displaystyle y=2-\frac<5>
График обратной пропорциональности
Как всегда, начнем с самого простого случая: \( \displaystyle y=\frac<1>
Таблица обратной пропорциональности (зависимости)
Нарисуем точки на координатной плоскости:
Теперь их надо плавно соединить, но как?
Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.
Это график гиперболы и выглядит он так:
Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.
Каждая из них стремится своими концами приблизиться к осям \( \displaystyle Ox\) и \( \displaystyle Oy\), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:
Оно и понятно: так как \( \displaystyle x\ne 0\), график не может пересекать ось \( \displaystyle Oy\). Но и \( \displaystyle y\ne 0\), так что график никогда не коснется и оси \( \displaystyle Ox\).
Ну что же, теперь посмотрим на что влияют коэффициенты.
На что влияют коэффициенты
Рассмотрим такие функции:
Ух ты, какая красота!
Все графики построены разными цветами, чтобы легче было их друг от друга отличать.
Итак, на что обратим внимание в первую очередь?
Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси \( \displaystyle Ox\).
Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.
А что, если функция выглядит сложнее, например, \( \displaystyle y=\frac<1>
В этом случае гипербола будет точно такой же, как обычная \( \displaystyle y=\frac<1>
Чему теперь не может быть равен \( x\)? Правильно, \( x\ne 1\). Значит, график никогда не достигнет прямой \( x=1\).
А чему не может быть равен \( y\)? Теперь \( y\ne 2\). Значит, теперь график будет стремиться к прямой \( y=2\), но никогда ее не пересечет.
Итак, теперь прямые \( x=1\) и \( y=2\) выполняют ту же роль, которую выполняют координатные оси для функции \( \displaystyle y=\frac<1>
Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):
Более подробно о том, как строятся такие графики, мы выучим чуть позже.
А теперь попробуй решить несколько примеров для закрепления.
Примеры
1. На рисунке изображен график функции \( \displaystyle y=\frac
2. На рисунке изображен график функции \( \displaystyle y=\frac
3. На рисунке изображен график функции \( \displaystyle y=\frac<1>
4. На рисунке изображен график функции \( \displaystyle y=\frac<1>
5. На рисунке приведены графики функций \( \displaystyle y=\frac
Функция обратной пропорциональности
Какая функция называется обратной пропорциональностью
Обратная пропорциональность представляет собой зависимость функции, при которой изменение независимой величины (аргумента) влечет пропорциональное изменение зависимой величины (функции).
Исходя из данного описания, во сколько раз увеличивается аргумент, во столько же раз уменьшается функция, и, наоборот, во сколько раз уменьшается аргумент, во столько же раз увеличивается функция.
Вы намерены приобрести в магазине апельсины. Фрукты на прилавке и сумма, которой вы располагаете, находятся в обратной пропорциональности. Это означает, что чем больше количество купленных вами апельсинов, тем меньше остаток денежных средств в вашем кошельке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Функцию обратной пропорциональности можно записать на математическом языке так:
В данной формуле переменные x и k — не равно нулю.
Свойства обратно пропорциональной функции
Гипербола — в математике это понятие обозначает плоскую кривую второго порядка, состоящую из двух частей.
Ветви гиперболы лежат в разных четвертях системы координат симметрично по отношению к началу координат (0; 0). Если коэффициент k принимает значения, больше нуля, то компоненты диаграммы располагаются в первой и третьей четвертях, если k меньше нуля — во второй и четвертой.
Особенности построения, пример
Пусть, функция задана формулой:
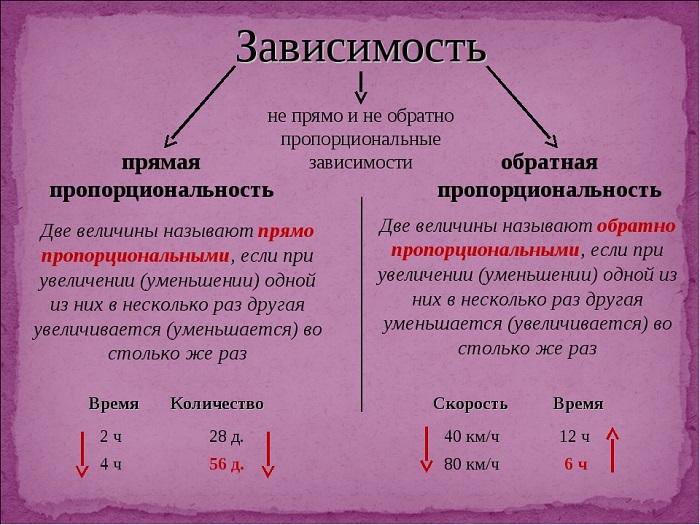
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график
Эта зависимость описывается следующей формулой:
Здесь k и называется коэффициентом пропорциональности.
Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k 0;
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Свойства функции обратной пропорциональности
области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.