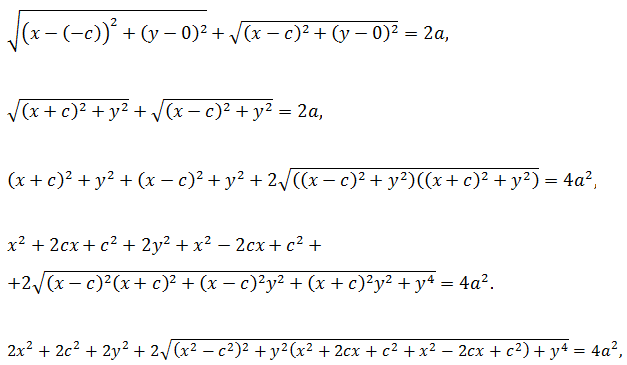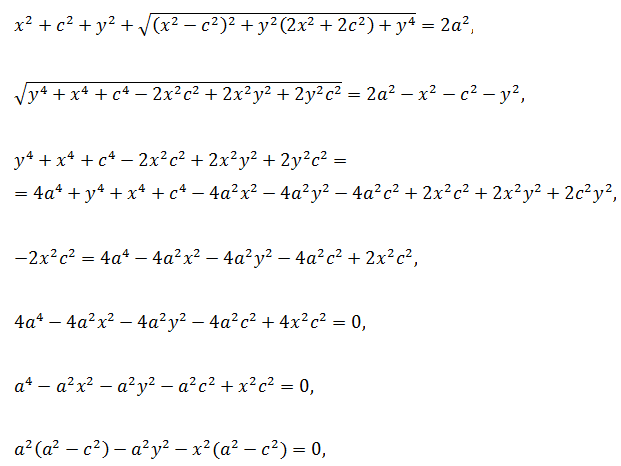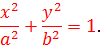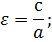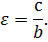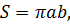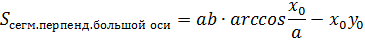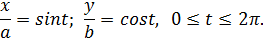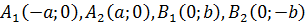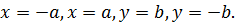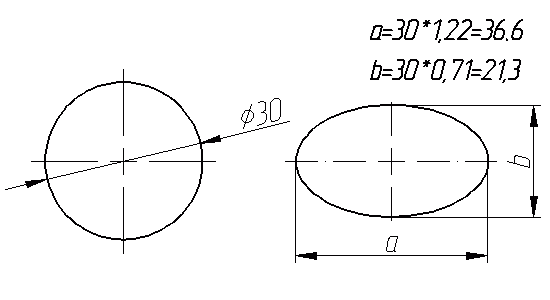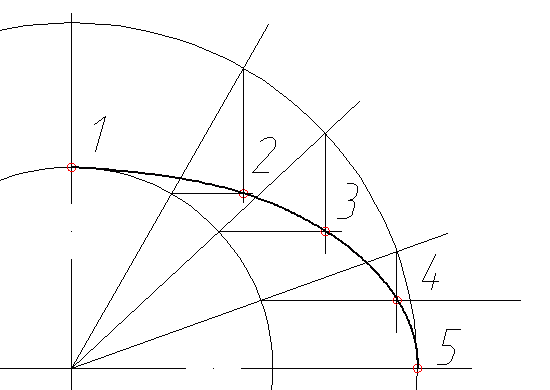Как построить эллипс по точкам
Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.
Определение и элементы эллипса
Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.
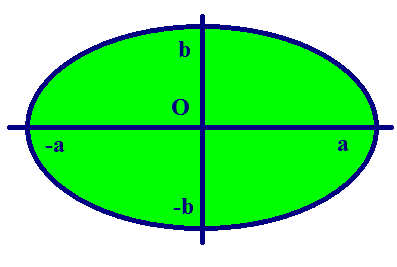
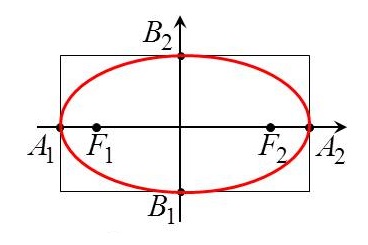
По форме график эллипса представляет замкнутую овальную кривую:
Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.
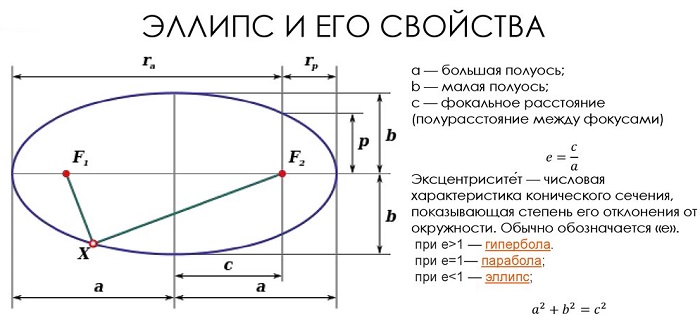
Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.
Точки эллипса, являющиеся концами осей, называются вершинами.
Расстояния от точки на линии до фокусов получили название фокальных радиусов.
Расстояние между фокусами есть фокальное расстояние.
Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.
Основные свойства эллипса
имеются две оси и один центр симметрии;
при равенстве полуосей линия превращается в окружность;
все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.
Уравнение эллипса
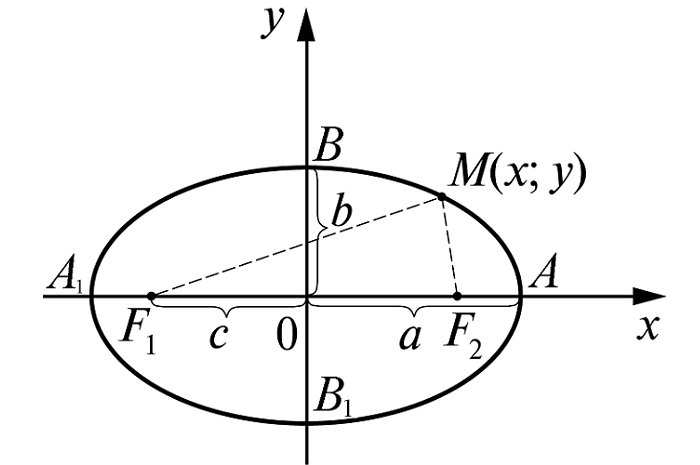
Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.
Для составления уравнения достаточно воспользоваться определением, введя обозначение:
а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);
c – половина фокального расстояния;
M(x;y) – произвольная точка линии.
В этом случае фокусы находятся в точках F1(-c;0); F2(c;0)
После ввода ещё одного обозначения
получается наиболее простой вид уравнения:
Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).
В случае (b b) формула эксцентриситета (ε) принимает вид:
Чем меньше эксцентриситет, тем более сжатым будет эллипс.
Площадь эллипса
Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:
a – большая полуось, b – малая.
Площадь сегмента эллипса
Часть эллипса, отсекаемая прямой, называется его сегментом.
Длина дуги эллипса
Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:
Радиус круга, вписанного в эллипс
В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:
Радиус круга, описанного вокруг эллипса
Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:
Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.
Как построить эллипс
Построение линии удобно выполнять в декартовых координатах в каноническом виде.
Строится прямоугольник. Для этого проводятся прямые:
Сглаживая углы, проводится линия по сторонам прямоугольника.
Полученная фигура есть эллипс. По координатам отмечается каждый фокус.
При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.
Как построить эллипс по точкам
Построение эллипса как аксонометрической проекции окружности начинается с определения положения центра и направления большой и малой осей эллипса. Размеры большой и малой осей рассчитывают или определяют графически и откладывают на чертеже A’B’ большая ось, C’D’ – малая. Затем через центр эллипса проводят вспомогательные прямые в направлении аксонометрических осей. В изометрии в направлении осей откладывается натуральный диаметр окружности 1-2 и 3-4. Полученные восемь точек соединяют плавной лекальной кривой. Построение изометрического эллипса по восьми точкам показано на рис. 171.
При построении диметрических эллипсов учитывается коэффициент искажения 0,5 направлении оси y. Построение диметрических эллипсов по восьми точкам показано на рис. 172.
Если восьми точек недостаточно, эллипс можно построить по двум осям (рис. 173). Этот способ можно применять и для построения эллипсов с произвольными размерами осей, например, для построения проекций окружности, лежащей в проецирующей плоскости.
Строят две окружности с диаметрами, равными большой и малой оси эллипса, и делят их радиальными отрезками на n частей. Затем из каждой точки пересечения большой окружности проводят вертикальные отрезки в сторону большой оси, а из точек пересечения с малой окружностью – горизонтальные отрезки в сторону от малой оси. Точки пересечения отрезков и являются точками эллипса. Полученные точки соединяют плавной лекальной кривой.
Эллипс — свойства, уравнение и построение фигуры
Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.
Определение и элементы эллипса
Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.
По форме график эллипса представляет замкнутую овальную кривую:
Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.
Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.
Точки эллипса, являющиеся концами осей, называются вершинами.
Расстояния от точки на линии до фокусов получили название фокальных радиусов.
Расстояние между фокусами есть фокальное расстояние.
Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.
Основные свойства эллипса
имеются две оси и один центр симметрии;
при равенстве полуосей линия превращается в окружность;
все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.
Уравнение эллипса
Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.
Для составления уравнения достаточно воспользоваться определением, введя обозначение:
а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);
c – половина фокального расстояния;
M(x;y) – произвольная точка линии.
В этом случае фокусы находятся в точках F1(-c;0); F2(c;0)
После ввода ещё одного обозначения
получается наиболее простой вид уравнения:
a 2 b 2 — a 2 y 2 — x 2 b 2 = 0,
Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).
В случае (b b) формула эксцентриситета (ε) принимает вид:
Чем меньше эксцентриситет, тем более сжатым будет эллипс.
Площадь эллипса
Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:
a – большая полуось, b – малая.
Площадь сегмента эллипса
Часть эллипса, отсекаемая прямой, называется его сегментом.
, где
(xo;y0) – крайняя точка сегмента.
Длина дуги эллипса
Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:
Радиус круга, вписанного в эллипс
В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:
Радиус круга, описанного вокруг эллипса
Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:
Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.
Как построить эллипс
Построение линии удобно выполнять в декартовых координатах в каноническом виде.
Строится прямоугольник. Для этого проводятся прямые:
Сглаживая углы, проводится линия по сторонам прямоугольника.
Полученная фигура есть эллипс. По координатам отмечается каждый фокус.
При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.
Как построить эллипс по точкам
Построение эллипса с помощью циркуля. Как начертить эллипс?
Чтобы не быть совсем абстрактным, я предлагаю начертить эллипс, являющийся отображением окружности в изометрии. Заодно вспомним коэффициенты искажения. Итак, возьмем окружность диаметром 30мм. Такая окружность в изометрии будет иметь вид эллипса с осями 36,6мм и 21,3 мм.
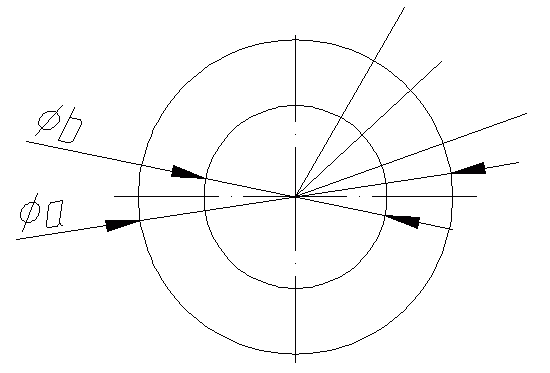
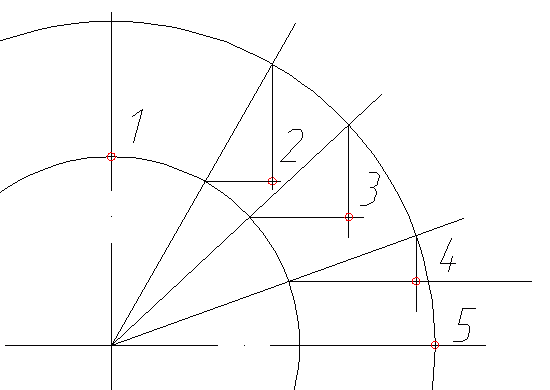
Начнем построение эллипса. На первом этапе необходимо из центра эллипса провести две вспомогательные окружности, диаметры которых будут равны большой и малой оси эллипса. Затем, из центра проведем несколько лучей, так чтоб они пересекали обе окружности. Для удобства отображения я буду рассматривать одну четверть. Количество вспомогательных лучей зависит исключительно от желаемой точности построений и размеров эллипса, в нашем случае это будут 3 луча (рекомендую такое количество лучей для эллипсов с большой осью от 60 и где-то до 120 мм)
На следующем шаге мы получим дополнительные точки эллипса. Для этого, мы поочередно сделаем с каждым лучем следующее: из точки пересечения луча с малой окружностью проведем горизонтальную линию в сторону большой окружности, а из точки пересечения луча с большой окружостью проведем линию до пересечения с только что начерченной горизонталью. Таким образом мы получим точки 2, 3 и 4. Точки 1 и 5 так же принадлежат эллипсу.
Теперь, имея пять точек мы без труда проведем через них кривую. Обратите внимание, что в точке пересечения с осями кривая эллипса строго перпендикулярна им.
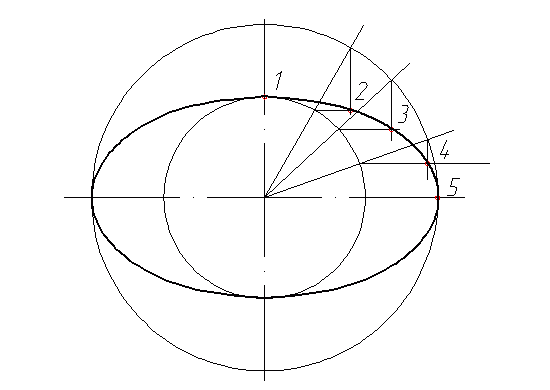
Нам осталось лишь достроить оставшиеся три четверти фигуры. Я рекомендую вам не производить аналогичные построения, а аккуратно перенести\отразить точки 2, 3, 4 через оси. Но конечно же, можно и повторить предыдущие шаги для закрепления навыка.
Вы можете сказать «спасибо!» автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»
Автор комментария: Рустам
Дата: 2011-03-22
Автор комментария: закир
Дата: 2011-05-19
огромное спасибо оч выручили.
Автор комментария: Вова
Дата: 2011-12-15
Автор комментария: Богдан Тарасюк
Дата: 2012-01-13
Автор комментария: ваня
Дата: 2012-01-24
Автор комментария: Виталий
Дата: 2012-05-13
Автор комментария: Леон
Дата: 2012-05-25
Благодарю! Все очень понятно обьяснили.
Автор комментария: антон
Дата: 2012-05-31
спасибо черчу через компас по вашим примерам вроде получается
Автор комментария: Влад
Дата: 2012-10-08
спасибо большое! все понятно. очень помогло
Автор комментария: Илья
Дата: 2012-10-09
но есть же способ проще. просто я его призабыл за пол года поэтому и зашел сюда
Точно, вы правы! Именно поэтому по тексту написано, что есть несколько способов, и мы рассмотрим один из них. Отмечу, что приведенный здесь способ (при достаточном количестве точек) дает максимальную точность построения.
Автор комментария: Женя
Дата: 2012-10-14
Спасибо. Очень помогло!
Автор комментария: Витя
Дата: 2012-10-22
Автор комментария: Нкитка
Дата: 2012-10-26
тупой способ циркулем намного проще и быстрей
Автор комментария: Татьяна
Дата: 2012-11-04
Автор комментария: Владимир
Дата: 2012-11-24
Спасибо в ремонте очень пригодилось!
Автор комментария: Светлана
Дата: 2012-12-17
Огромное спасибо!Все просто и доступно!
Благодарю за отзыв, Светлана! Слова такого плана меня всегда наводят на мысль: а почему те люди, которые получают от нашего государства деньги за написание методических пособий, делают это не просто, не понятно, и не доступно? Очень надеюсь, что они это не специально
Автор комментария: Женя
Дата: 2013-01-21
а точки от руки соединять? как-то у меня не очень ровно получается.
Автор комментария: ДАНИИЛ
Дата: 2013-01-21
СЕРДЧЕЧНАЯ БЛАГОДАРНОСТЬ ЗА ВАШ ТРУД
sposibo ochen pomoglo
Автор комментария: рома
Дата: 2013-03-12
Великолепно!) спасибо большое!)
Автор комментария: Анатолий.
Дата: 2013-07-07
Спасибо! Очень понятно и доступно расказано о построение элипса. С геометрией у меня все в порядке, а вот элипсы строить не доводилось. По Вашей методике постою элипс на потолке, теперь точно получится! Спасибо еще раз.
Автор комментария: Павел
Дата: 2013-07-09
Спасибо огромное всен очень понятно объяснено!
Автор комментария: Андраник
Дата: 2013-07-18
Большое спасибо! Выручил.
Автор комментария: Владислав
Дата: 2013-09-04
Спасибо! Потребовалось прорезать точное отверстие под круглый дымоход в наклонной плоскости, Ваш метод построения эллипса очень помог!
Автор комментария: фариза
Дата: 2014-01-09
так просто,только есть один вопрос,можете сказать расстояний между точками (1,2,3,4,5)
Автор комментария: 999
Дата: 2014-02-16
«Теперь, имея пять точек мы без труда проведем через них кривую» Они что издеваются?!
Автор комментария: сережа
Дата: 2014-03-06
как начертить машину в компасе
Автор комментария: Александр
Дата: 2014-03-11
Автор комментария: Андрей
Дата: 2014-05-03
Благодарен всё ясно, просто и понятно.
Автор комментария: Светлана
Дата: 2014-05-17
Автор комментария: Majid Shabanov
Дата: 2014-06-17
Большое спасибо! Очень доступном виде обьяснили, без лищных слов.
Автор комментария: arhitektor stroitel
Дата: 2014-07-06
http://oval.ing-grafika.ru/1.html 2 способ посмотрите.Он удобнее вроде.
Автор комментария: Альбина
Дата: 2014-09-28
Cпасибо! Очень доступно изложено) Здорово получилось)))
Автор комментария: наталья
Дата: 2014-10-12
огромное Вам спасибо
Автор комментария: алик
Дата: 2014-11-25
Большое человеческое СПАСИБО
Автор комментария: Юля
Дата: 2014-12-10
Автор комментария: Александр
Дата: 2015-01-06
Принцип построения изложен предельно понятно. Однако, не изложено объяснение того, что в результате проведенных операций должен получиться именно эллипс, а не овал. Я понимаю, что принцип построения эллипса правильный, но нет объяснения почему.
Автор комментария: Роман
Дата: 2015-03-02
Спасибо! Реально доступно объяснили! Очень помогло.
Автор комментария: Міша
Дата: 2015-03-03
Дуже дякую виручили, дуже допомогло)))) +1
Автор комментария: Илья
Дата: 2015-03-19
По поводу «тупой способ циркулем намного проще и быстрей». Это как?
Автор комментария: :O
Дата: 2015-11-25
Черт.. Это так просто!
Автор комментария: Елизавета
Дата: 2016-02-04
СПАСИБО! не была на паре, задали дома по определенным размерам начертить, просто спасли!
Автор комментария: j
Дата: 2016-10-22
Автор комментария: Владимир
Дата: 2017-01-10
Всё просто, спасибо за комментарии.
Автор комментария: Рустем
Дата: 2017-04-17
Автор комментария: Володя
Дата: 2018-01-17
У вас уже заданны большой и малый диаметры зллипса, прошу к данному варианту добавить метод засечек исходя только из данных диаметра круга. С.У.Стенин.
Автор комментария: Александр
Дата: 2018-02-02
Великолепно. просто,доходчиво и без лишней информации!!
Автор комментария: Дамир
Дата: 2018-04-03
Автор комментария: саня
Дата: 2018-06-13
Добавьте свой комментарий:
Наша страница в ВК:
Антон, у вас офис только в Москве? или в других городах тоже есть?
Содержание:
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
, т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 
, есть величина постоянная (большая, чем расстояние между 
).
Если а =Ь, то уравнение (7.3) можно переписать в виде:
(7.5)
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 
координаты которой задаются формулами 
будет окружность (4) переводить в эллипс, заданный соотношением 
Число 
называется эксцентриситетом эллипса. Эксцентриситет 
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 
становится более вытянутым
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 
).
Тогда 
А расстояние 
Подставив в формулу r=d, будем иметь
. Возведя обе части равенства в квадрат, получим
или
(9.4.1)
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
также определяют параболы.
Легко показать, что уравнение 
, определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а 
О. Для этого выделим полный квадрат:
и сделаем параллельный перенос по формулам
Пример:
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю 
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
которое называют каноническим уравнением эллипса.
Число а называют большей полуосью эллипса, число 
— мень-
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
и определяет окружность радиуса а с центром в начале координат.
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 
и характеризует форму эллипса. Для окружности 
Чем больше эксцентриситет, тем более вытянут эллипс.
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
— каноническое уравнение эллипса с центром в точке 
большей полуосью а=3 и меньшей полуосью 
Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 
а оси 
параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е. 
В новой системе координат координаты 
вершин и фокусов гиперболы будут следующими:
Переходя к старым координатам, получим:
Построим график эллипса.
Задача решена.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.