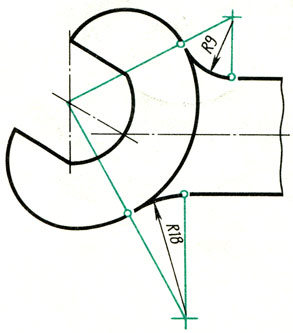
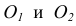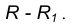Как построить дугу на чертеже

Как построить дугу на чертеже

§ 9. Сопряжения

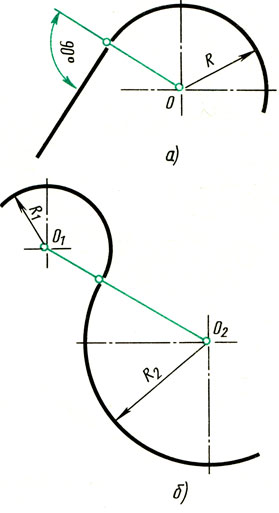
Плавный переход прямой линии в дугу или одной дуги в другую называют сопряжением. Для построения сопряжения надо найти центры, из которых проводят дуги, т. е. центры сопряжений (рис. 63). Затем нужно найти точки, в которых одна линия переходит в другую, т. е. точки сопряжений. При построении контура изображения сопрягающиеся линии нужно доводить точно до этих точек. Точка сопряжения лежит на перпендикуляре, опущенном из центра О дуги на сопрягаемую прямую (рис. 64, а), или на линии О₁О₂, соединяющей центры сопрягаемых дуг (рис. 64, б). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку сопряжения.

Рис. 63. Элементы сопряжений

Рис. 64. Определение точки сопряжения

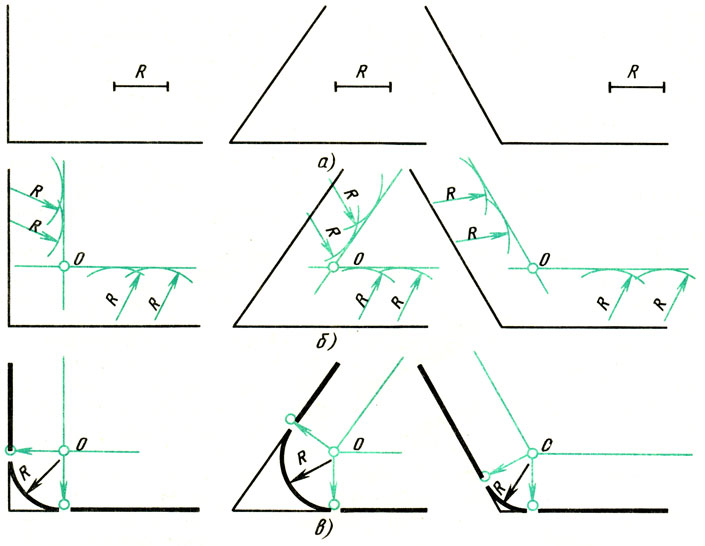
Сопряжение двух пересекающихся прямых дугой заданного радиуса. Даны пересекающиеся под прямым, острым и тупым углами прямые линии (рис. 65, а). Нужно построить сопряжения этих прямых дугой заданного радиуса R.

Для всех трех случаев применяют общий способ построения.

Для построения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные.

2. Находят точки сопряжений (рис. 65, в). Для этого опускают перпендикуляры из точки О на заданные прямые.

3. Из точки О, как из центра, описывают дугу заданного радиуса R между точками сопряжений (рис. 65, в).

Рис. 65. Сопряжение двух пересекающихся прямых

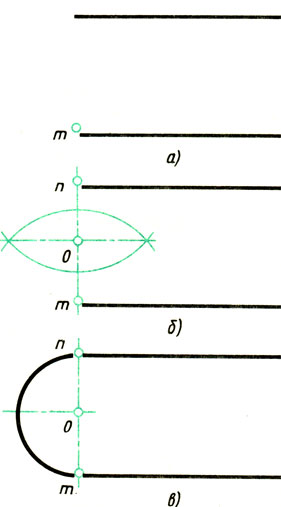
Сопряжение двух параллельных прямых. Заданы две параллельные прямые и на одной из них точка сопряжения т (рис. 66, а). Требуется построить сопряжение.

Построение выполняют следующим образом:

1. Находят центр сопряжения и радиус дуги (рис. 66, б). Для этого из точки m на одной прямой восставляют перпендикуляр до пересечения с другой прямой в точке п. Отрезок делят пополам (см. рис. 56).

Рис. 66. Сопряжение двух параллельных прямых

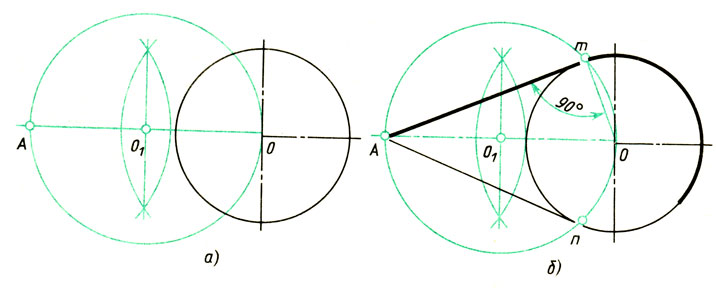
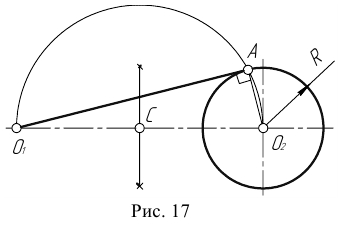
Проведение касательной к окружности. Задана окружность с центром О и точка А (рис. 67, а). Требуется провести из точки А касательную к окружности.

1. Точку А соединяют прямой с заданным центром О окружности.

Строят вспомогательную окружность диаметром, равным ОА (рис. 67, а). Чтобы найти центр О₁ делят отрезок ОА пополам (см. рис. 56).

Рис. 67. Построение касательной к двум окружностям

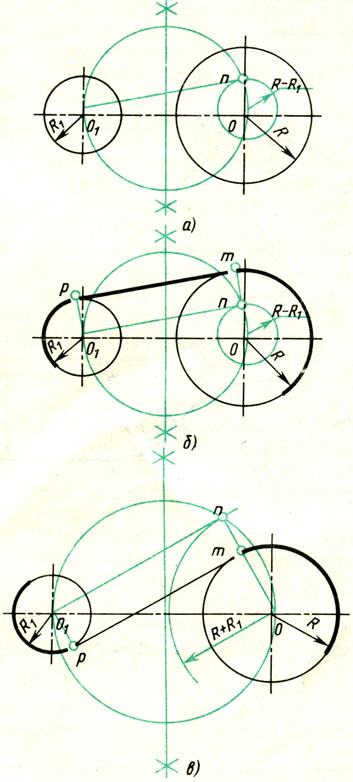
Проведение прямой, касательной к двум окружностям. Заданы две окружности радиусом R и R₁. Требуется построить касательную к ним.

Различают два случая касания: внешнее (рис. 68, б) и внутреннее (рис. 68, в).

При внешнем касании построение выполняют следующим образом:

2. Радиус, проведенный из точки О в точку n, продолжают до пересечения в точке m с заданной окружностью радиусом R. Параллельно радиусу Оm проводят радиус 0₁р меньшей окружности. Прямая, соединяющая точки сопряжений m и р,- касательная к заданным окружностям (рис. 68, б).

При внутреннем касании построение проводят аналогично, но вспомогательную окружность проводят радиусом, равным сумме радиусов R + R₁ (см. рис. 68, в). Затем из центра O₁ проводят касательную к вспомогательной окружности (см. рис. 67). Точку n соединяют радиусом с центром О. Параллельно радиусу On проводят радиус O₁р меньшей окружности. Искомая касательная проходит через точки сопряжений m и р.

Рис. 68. Построение касательной к окружности

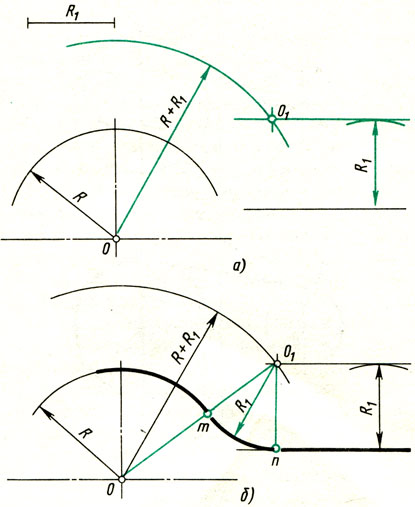
Сопряжение дуги и прямой линии дугой заданного радиуса. Заданы дуга окружности радиусом R и прямая. Требуется соединить их дугой радиусом R₁.

1. Находят центр сопряжения (рис. 69, а), который должен находиться на расстоянии R₁ от дуги и от прямой. Такому условию соответствует точка пересечения прямой линии, параллельной заданной прямой, проходящей от нее на расстоянии R₁, и вспомогательной дуги, отстоящей от заданной также на расстоянии R₁. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R₁ (рис. 69, а). Раствором циркуля, равным сумме заданных радиусов R + R₁, описывают из центра О дугу до пересечения с вспомогательной прямой. Полученная точка O₁— центр сопряжения.

2. По общему правилу находят точки сопряжения (рис. 69, б). Соединяют прямой центры сопрягаемых дуг O₁ и О. Опускают из центра сопряжения O₁ перпендикуляр на заданную прямую.

3. Из центра сопряжения O₁ между точками сопряжения m и n проводят дугу, радиус которой равен R 1 (см. рис. 69, б).

Рис. 69. Сопряжение дуги окружности и прямой

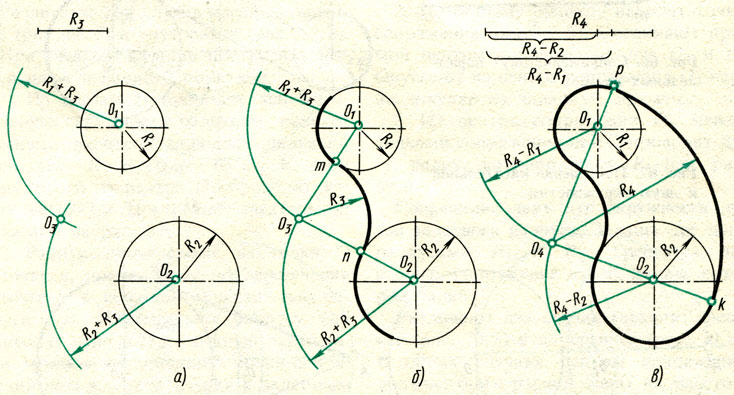
Сопряжение двух дуг окружности дугой заданного радиуса. Заданы две дуги радиусами R₁ и R₂. Требуется построить сопряжение дугой, радиус которой задан.

Различают два случая касания: внешнее (рис. 70, б) и внутреннее (рис. 70, в). В обоих случаях центры сопряжений должны быгь расположены на расстоянии, равном радиусу дуги сопряжения, от заданных дуг. По общему правилу на прямых, соединяющих центры сопрягаемых дуг, находят точки сопряжения.

Ниже приведен порядок построения для внешнего и внутреннего касаний.

2. Соединив прямыми точку O₁ с точкой O₃ и точку O₂ с точкой O₃, находят точки сопряжения m и n (см. рис. 70, б),

3. Из точки О₃ раствором циркуля, равным R₃, между точками m и n описывают сопрягающую дугу.

Для внутреннего касания выполняют те же построения, но радиусы дуг берут равными разности радиусов сопрягающей и заданной дуг, т.е. R₄-R₁ и R₄-R₂. Точки сопряжения р и k лежат на продолжении линий, соединяющих точку О₄ с точками O₁ и O₂.

Рис. 70. Сопряжение двух дуг окружности

Источник

Сопряжения в инженерной графике на чертежах с примерами

Содержание:

В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.

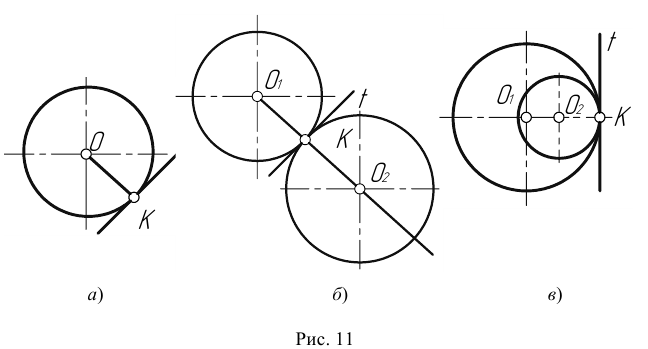
Точка касания К и центры окружностей

Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.

Сопряжение двух пересекающихся прямых линий

Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.

Выполним следующие построения:

Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.

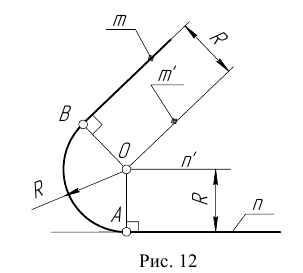
Сопряжения прямой с окружностью

Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.

Пример 1. Пусть задана окружность радиусом R с центром в точке 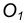и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 13).

Для решения задачи выполним следующие построения:

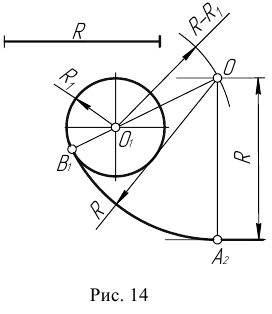
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 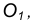, радиусом

Сопряжение двух окружностей

Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.

Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 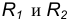дугой заданного радиуса R (рис. 15а).

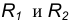
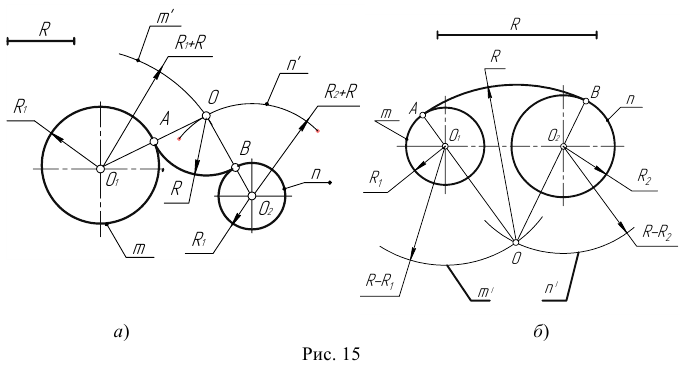
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами дугой радиусом R (рис. 15б).

Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.

Построение касательных

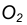
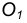
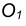
Пример 1. Дана окружность с центром в точке и точка вне её. Через данную точку провести касательную к данной окружности (рис. 17).

Для решения задачи выполним следующие построения.

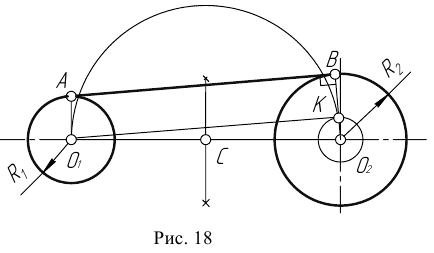
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 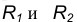(рис. 18).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Сопряжения

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

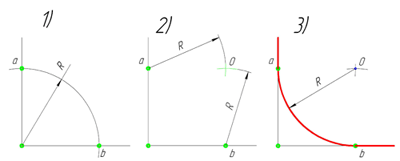
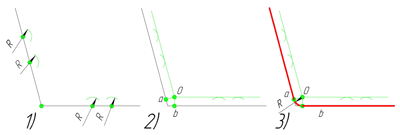
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

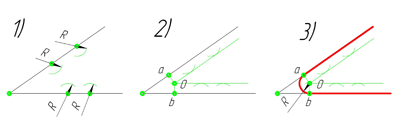
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Сопряжение параллельных прямых линий

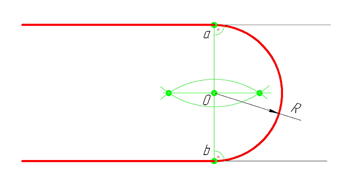
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

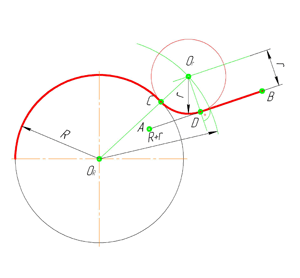
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Внутреннее сопряжение прямой линии с дугой

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

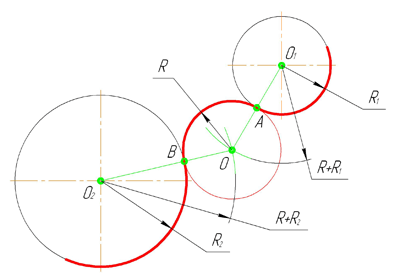
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

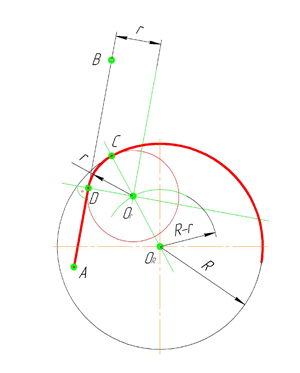
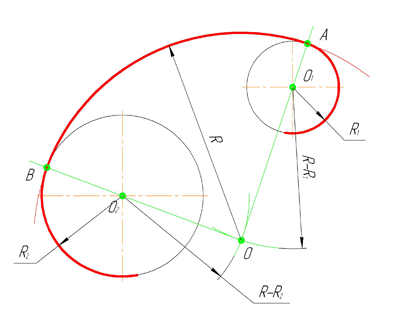
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Источник

Как построить дугу на чертеже

Из многочисленных построений здесь рассматрива­ются только те, которые часто встречаются при вы­полнении чертежей.

Деление отрезка прямой на две и четыре равные части выполняется в следующей последовательности.

Из концов отрезка А В циркулем проводят две дуги окружности радиусом R, несколько большим поло­вины данного отрезка, до взаимного пересечения в точках n и m (рис. 43, а). Точки тип соединяют пря­мой, которая пересекает отрезок АВ в точке С. Точка С делит отрезок А В на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка СВ, разделим отрезок на четыре равные части.

При вычерчивании детали, показанной на рис. 43, б, применяется способ деления отрезка на четыре части.

Деление отрезка прямой на любое число равных частей. Пусть отрезок А В требуется разделить на И равных частей. Для этого из любого конца данного отрезка, например из точки В (рис. 44, проводят под произвольным острым углом вспомогательную прямую линию ВС, на которой от точки В измеритель­ным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой А прямой Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой которые и разделяют отрезок А В на 11 равных частей.

На рис. 44, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части.

ПОСТРОЕНИЕ И ИЗМЕРЕНИЕ УГЛОВ ТРАНСПОРТИРОМ

Транспортир — это прибор для измерения и построе­ния углов. Это полукруг с разбивкой на градусы, сое­диненный с опорной планкой.

Для измерения угла транспортир прикладывают опорной планкой к одной из сторон данного угла (рис. 45, а) так, чтобы вершина угла (точка А) совпадала с точкой О на транспортире. Величину угла САВ в гра­дусах определяют по шкале транспортира.

Для построения угла заданной величины (в градусах) со стороной А В и вершиной в точке к приклады­вают транспортир так, чтобы его центр (точка О) сов­пал с точкой А прямой АВ, затем у деления шкалы транспортира, соответствующего заданному числу градусов (например, 55°), наносят точку n. Транспортир убирают и проводят через точку n отрезок АС — полу­чают заданный угол САВ (рис. 45, б).

Углы можно строить при помощи угольников с углами 45, 30 и 60° и линейки или рейсшины. На рис. 46 показано, как при различных положениях угольников на рейсшине можно строить углы 60 (120), 30 (150), 45° (135°) и другие при использовании одновременно двух угольников..

ПОСТРОЕНИЕ И ДЕЛЕНИЕ УГЛОВ

Деление угла на две и четыре равные части. Из вер­шины угла провести произвольным радиусом дугу до пересечения со сторонами угла в точках (рис. 47, а). Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги n и к, до взаимного пересечения в точке m. Вершину угла соединяют с точкой т прямой, которая делит угол ВАС пополам. Эта прямая называется биссектрисой угла ВАС. Повторяя это построение с полученными углами В Ат и nАС угол ВАС можно разделить на четыре равные части и т. д.

Деление прямого угла на три равные части. Из вер­шины А прямого угла (рис. 47, б) произвольным ради­усом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла А прямыми и получают стороны Аm и Аn углов В Аm и nА С,равных 1/3 прямого угла, т. е. 30°. Если каждый из этих углов разделить пополам, то пря­мой угол будет разделен на шесть равных частей, ка­ждый из углов будет равняться 15°. Прямой угол АВС можно разделить на три равные части угольником с углами 30 и 60° (рис. 48, а). При выполнении чертежей нередко требуется разделить прямой угол на две рав­ные части. Это можно выполнять угольником с углом 45° (рис. 48, б).

Построение угла, равного данному. Пусть задан угол ВАС. Требуется построить такой же угол. Через произвольную точку А₁ проводим прямую А₁С₁. Из точки А описываем дугу произвольным радиусом R, которая пересечет угол ВАС в точках (рис. 49,а). Из точки A ₁ проводим дугу тем же радиусом и полу­чаем точку m₁. Из точки A₁ проводим дугу радиусом R₁ равным отрезку mn, до пересечения с ранее прове­денной дугой радиуса R в точке n₁ (рис. 49, б). Точку n₁ соединяем с точкой А₁ и получаем угол B₁A₁C₁ вели­чина которого равна заданному углу ВАС.

Применение вышеизложенного построения угла по заданному показано на рис. 49, в и г. На рис. 49, в изоб­ражена деталь, чертеж которой надо вычертить, а на рис. 49, г показан этот чертеж, при выполнении кото­рого использован способ построения угла по заданно­му.

СПОСОБЫ ПОСТРОЕНИЯ МНОГОУГОЛЬНИКОВ

Способ триангуляции. Построение многоугольников этим способом основано на последовательном построе­нии ряда треугольников, примыкающих сторонами друг к другу. Этот способ будет применяться в дальней­шем при построении разверток поверхностей геоме­трических тел.

Рассмотрим пример такого построения. На рис. 50, а показана пластина с пятиугольным отверстием. Изме­ряя длины сторон пятиугольника, можно построить на чертеже контурное очертание многоугольного отвер­стия.

Треугольники в рассматриваемом многоугольнике можно получить, проведя диагонали 14 (рис. 50, а). Последовательность построения многоугольника на чертеже в данном примере следующая.

На детали произвольно выбираем базовую линию (например, А В), на которую из точек 7 и 2 опускаем перпендикуляр, и получаем точки E и G. На чертеже наносим базовую линию A₁B₁ на которой откладываем отрезок E₁G₁ равный отрезку EG. Из точек и G, восставляем перпендикуляры, на которых отклады­ваем взятые с детали отрезки и G1 (рис. 50, б). Получим точки 1₁и2₁. Из точек как из центров, циркулем описываем две дуги радиусами, равными отрезками 13 и 23, взятых с детали. Точка пересечения дуг является вершиной 3₁ искомого треугольника 1₁2₁3₁. Таким же способом из точек 7₁ и 3₁ описываем две дуги радиусами, равными отрезкам 34 и 14, нахо­дим вершину 4₁. Затем из точек 4₁ и 1₁, как из центров, описываем две дуги радиусами, равными отрезкам 45 и 15, определяем последнюю вершину пятиугольника 5₁(рис. 50, б).

ОПРЕДЕЛЕНИЕ ЦЕНТРА ДУГИ ОКРУЖНОСТИ

Многие детали машин и приборов имеют контур очертания, состоящий из прямых линий, лекальных кривых и дуг окружностей. При вычерчивании деталей часто приходится определять величину радиусов дуг окружностей контурных очертаний детали и находить положение центров этих дуг. На рис. 51, а показана деталь (кронштейн), левая часть ребра которой выполнена по дуге окружности.

Чтобы найти положение центра и величину радиуса данной дуги, предварительно делают отпечаток дуги на бумаге. При помощи циркуля и линейки можно определить центр и размер радиуса дуги окружности, для этого на отпечатке дуги намечают три произ­вольно расположенные на ней точки А, В и С (рис. 51, б) и проводят хорды АВ и ВС. При помощи циркуля и линейки проводят перпендикуляры через середины хорд А В и ВС. Точка пересечения перпендикуляров

(точка О) является искомым центром дуги детали, а расстояние от точки О до любой точки дуги будет раз­мером радиуса.

ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ

Некоторые детали машин и приборов имеют эле­менты, равномерно расположенные по окружности, например, детали на рис. 52—59. При выполнении чер­тежей подобных деталей необходимо знать правила деления окружности на равное количество частей.

Деление окружности на четыре и восемь равных частей. На рис. 52, а показана крышка, в которой име­ется восемь отверстий, равномерно расположенных по окружности. При построении чертежа контура крышки (рис. 52 г) необходимо разделить окружность на восемь равных частей. Это можно сделать с помощью угольника с углами 45° (рис. 52, в), гипоте­нуза угольника должна проходить через центр окруж­ности, или построением.

Два взаимно перпендикулярных диаметра окружно­сти делят ее на четыре равные части (точки 7, 3, 5, 7 на рис. 52, б). Чтобы разделить окружность на восемь равных частей, применяют известный прием деления прямого угла с помощью циркуля на две равные части. Получают точки 2, 4, 6, 8.

Деление окружности на три, шесть и двенадцать рав­ных частей. Во фланце (рис. 53, а) имеется три отвер­стия, равномерно расположенных по окружности. При выполнении чертежа контура фланца (рис. 53, г) нужно разделить окружность на три равные части.

Для нахождения точек, делящих окружность радиуса R на три равные части, достаточно из любой точки окружности, например точки А, провести дугу ради­усом R. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет нахо­диться на пересечении оси окружности, проведенной из точки Л, с окружностью (рис. 53, б).

Разделить окружность на три равные части можно также угольником с углами 30 и 60° (рис. 53, в), гипотенуза угольника должна проходить через центр окруж­ности.

Разделить окружность на шесть равных частей можно и угольником с углами 30 и 60° (рис. 54, в). На рис. 54, а показана крышка, при выполнении чертежа которой необходимо выполнить деление окружности на шесть частей.

Чтобы выполнить чертеж детали (рис. 55, а), кото­рая имеет 12 отверстий, равномерно расположенных по окружностям, нужно разделить осевую окружность на 12 равных частей (рис. 55, г).

При делении окружности на 12 равных частей с помощью циркуля можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 54, б),но дуги радиусом R описывать четыре раза из точек 1, 7, 4и 10 (рис. 55, б).

Используя угольник с углами 30 и 60° с последующим поворотом его на 180°, делят окружность на 12 равных частей (рис. 55, в).

Деление окружности на пять, десять и семь равных частей. В плашке (рис. 56, а) имеется пять отверстий, равномерно расположенных по окружности. Выпол­няя чертеж плашки (рис. 56, в), необходимо разделить окружность на пять равных частей. Через намеченный центр О (рис. 56, б)

Деталь «звездочка» (рис. 57, а) имеет 10 одинаковых элементов, равномерно расположенных по окружно­сти. Чтобы выполнить чертеж звездочки (рис. 57, я), следует окружность разделить на 10 равных частей. В этом случае следует применить то же построение, что и при делении окружности на пять частей (см. рис. 56, б). Отрезок п₁ будет равняться хорде, которая делит окружность на 10 равных частей.

На рис. 58, а изображен шкив, а на рис. 58, в — чер­теж шкива, где окружность разделена на семь равных частей.

Деление окружности на любое число равных частей. С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (табл. 9).

При построении чертежа кольца (рис. 59, а) необхо­димо окружность диаметра D=142 мм разделить на 32 равные части. Количеству частей окружности n=32 соответствует коэффициент k=0,098. Подсчитав длину хорды l=Dk=142×0,098= 13,9 мм, ее циркулем откла­дывают на окружности 32 раза (рис. 59, б и в).

Источник