Как посчитать верхний квартиль в эксель
Примеры функции КВАРТИЛЬ в Excel для расчета медианы квартиля
Функция КВАРТИЛЬ в Excel используется для расчета квартиля диапазона числовых данных и возвращает соответствующее числовое значение.
Функция КВАРТИЛЬ.ВКЛ вычисляет на основе указанной процентили в качестве второго аргумента функции. Полностью соответствует первой функции. Последняя используется в Excel 2007 и более ранних версиях и оставлена для совместимости.
Функция КВАРТИЛЬ.ИСКЛ используется для расчета квартили диапазона числовых значений на основе известной процентили, за исключением граничных значений (минимального и максимального значения в диапазоне).
Квартили используются для распределения диапазона чисел на четыре равные части:
Функция КВАРТИЛЬ.ВКЛ может быть использована не только для определения медианы выборки (второго квартиля), а и нахождения минимального и максимального значений соответственно. При работе с большими диапазонами чисел для подобных расчетов рекомендуется использовать функции МИН и МАКС соответственно.
Существует несколько алгоритмов расчета квартилей. Все рассмотренные функции используют следующую формулу:
Для расчета индекса квантиля (x) функция КВАРТИЛЬ.ВКЛ используют формулу:
x=(n-1)p, где n – количество элементов в диапазоне.
Функция КВАРТИЛЬ.ИСКЛ использует формулу x=(n+1)p.
В Excel принято так, что первые выше указанные 2 функции используют метод N-1-интерполяцию, а третья функция – N+1-интерполяцию.
Примеры использования функций КВАРТИЛЬ в Excel
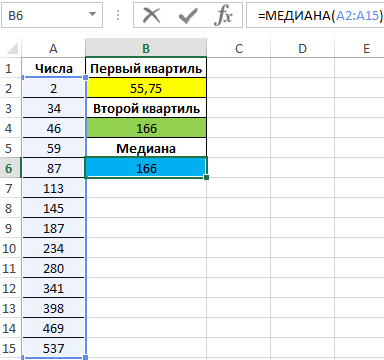
Вид таблицы данных:
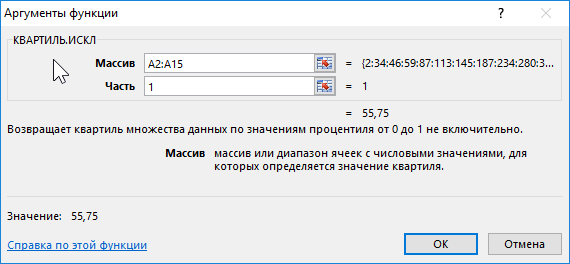
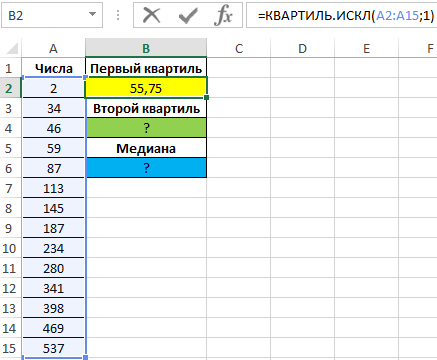
Для определения 1-го квартиля используем функцию:
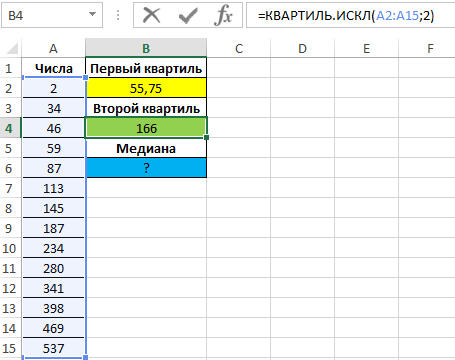
Проверим утверждение о том, что второй квартиль соответствует медиане выборке. Определим 2-й по формуле:
Полученные значения совпадают:
В результате расчетов мы получили первый, второй квартили и медиану для исходного диапазона чисел.
Статистический анализ роста доли дохода в Excel за период
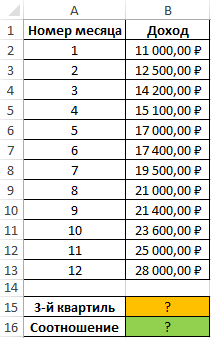
Пример 2. В таблице приведены данные о доходах предпринимателя за год. Доказать, что примерно 75% значений меньше, чем третий квартиль доходов.
Вид исходной таблицы:
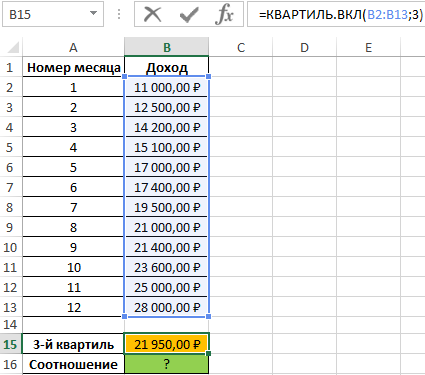
Определим 3-й по формуле:
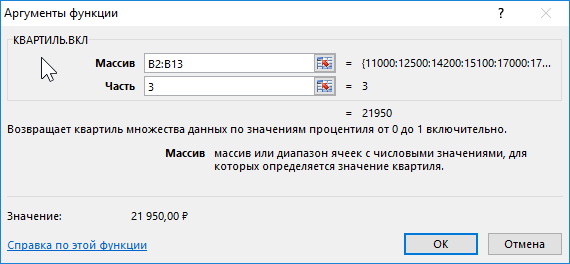
Определим соотношение чисел, меньше полученного числа, к общему количеству значений по формуле:
=СЧЁТЕСЛИ(B2:B13;» Пример 3. Имеется диапазон случайных чисел, отсортированный в порядке возрастания. Определить соотношение суммы чисел, которые меньше 1-го квартиля, к сумме чисел, которые превышают значение 1-го квартиля.
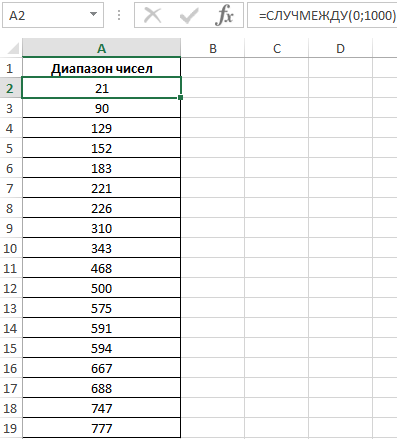
Чтобы сгенерировать случайное число в Excel воспользуемся функцией:
После генерации отсортируем случайно сгенерированные числа по возрастанию. Вид исходной таблицы данных со случайными числами:
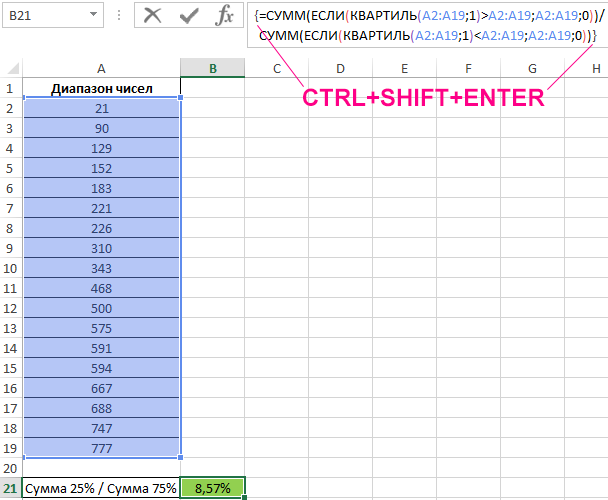
Формула для расчета имеет следующий вид (формула массива CTRL+SHIFT+ENTER):
Функции СУММ с вложенными функциями ЕСЛИ выполняют расчет суммы только тех чисел, которые меньше и больше соответственно значения, возвращаемого функцией для исследуемого диапазона. Из полученных значений вычисляется частное. Результат расчетов:
Общая сумма чисел исследуемого диапазона, которые меньше 1-го квартиля, составляет всего 8,57% от общей суммы чисел, которые больше 1-го квартиля.
Особенности использования функций расчета квартиля в Excel
Все рассматриваемые функции имеют одни и те же аргументы:
Примеры формул для расчета квартиля в Excel
Разделение данных на равные доли, позволяет узнать и наглядно отобразить какая доля приходится на группу значений по отношению ко всем другим общим значениям. Рассмотрим на примерах, как в Excel сделать равномерное сегментирование данных.
Как посчитать квартиль в Excel
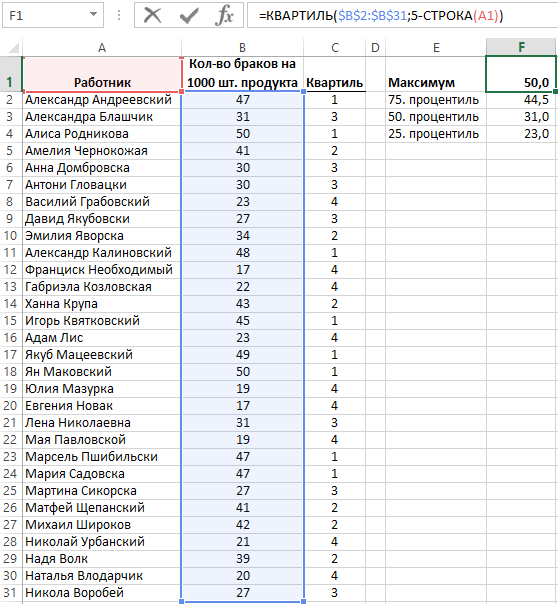
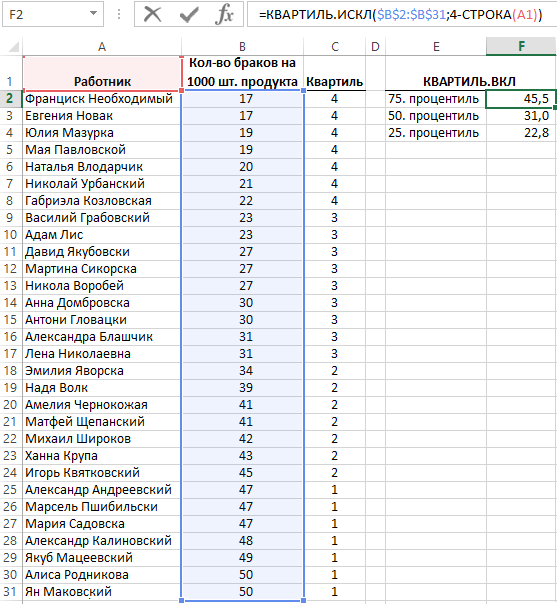
Ниже на рисунке представлен список работников предприятия производящих определенный продукт, а также статистические показатели количества браков на 1000 шт. готовой производимой продукции выкрытые отделом контроля качества. Цель в данном примере найти наилучших работников и тех, которым требуется повышение квалификации. Для этого разделим данные на 4 равные доли. Для определения границ значений каждой 4-й доли Excel предлагает функцию КВАРТИЛЬ. Термин квартиль обозначает граничный раздел значения, содержащий ¼ долю 25% данных.
В ячейке используется следующая формула для определения квартиля охватывающего наибольшие значения:
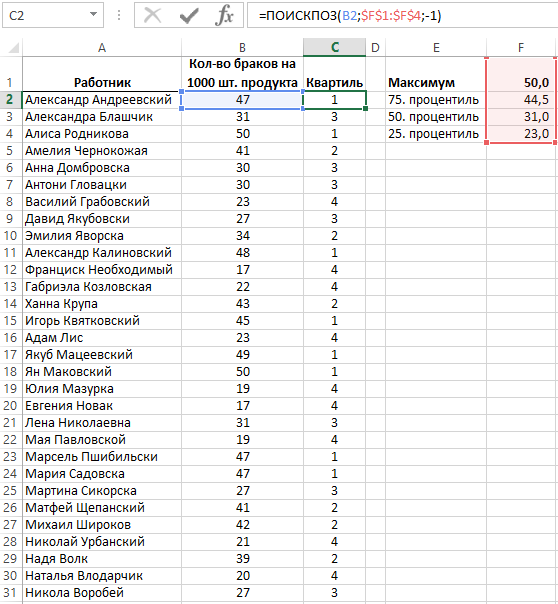
Функция КВАРТИЛЬ служит для вычисления границ раздела для исходных значений. Формула в ячейке C2 на рисунке определяет номер квартиля, в котором находится значение с ячейки B2. Формула скопирована в очередные ячейки ниже с целью преобразования всех значений в соответственные квартили и имеет следующий вид:
Функция КВАРТИЛЬ требует указания диапазона значений в первом аргументе, а во втором аргументе целое число определяющее номер квартиля, для которого граничное значение должно быть найдено. Допустимое значение для второго аргумента – это:
Если же номер квартиля не находится в границах значения 0 – 4, формула возвращает ошибку. Если же номер квартиля является дробным числом, тогда все цифры после запятой отбрасываются и используется только целая часть аргумента.
В формуле ячейки F1 второй аргумент функции КВАРТИЛЬ содержит не число, а формулу: 5-СТРОКА(A1), которая позволяет уменьшать номер квартиля на 1 во время копирования формулы в очередные нижние ячейки. Выражение в ячейке F1 возвращает значение 4, означающее номер квартиля с наибольшими значениями. Во время копирования формулы в ячейки находящихся под ячейкой F1 ссылка A1 сменяется на А2 и формула возвращает число 5-3, то есть 3 в ячейке F2, которое значит границу 75-го процентиля.
Функция ПОИСКПОЗ возвращает номер позиции, на которой в списке была найдено исходное значение. Она прекратит свое вычисление если очередное значение будет меньше от искомого. Если бы искомым значением было бы число 47, тогда ПОИСКПОЗ приняла что (44,5) является меньшим от искомого и прекратила бы свое вычисление уже на первой позиции.
Альтернативная функция КВАРТИЛЬ.ИСКЛ в Excel
Какой наилучший способ вычисления границ квартиля – это все еще актуальная тема для многих дискуссий. В старых версиях программы Excel была доступна только лишь функция КВАРТИЛЬ. Ее алгоритм вычисления основан на формуле n%*(число-1). Начиная с версии Excel 2010, можно воспользоваться более новыми функциями для решения такого рода задач, но уже другими методами вычисления. Функция КВАРТИЛЬ.ВКЛ работает аналогично, как и обычная по тому же алгоритму. Старую функцию так же оставили для поддержки старых версий файлов Excel. А функция КВАРТИЛЬ.ИСКЛ использует другую формулу алгоритма: n%*(число+1).
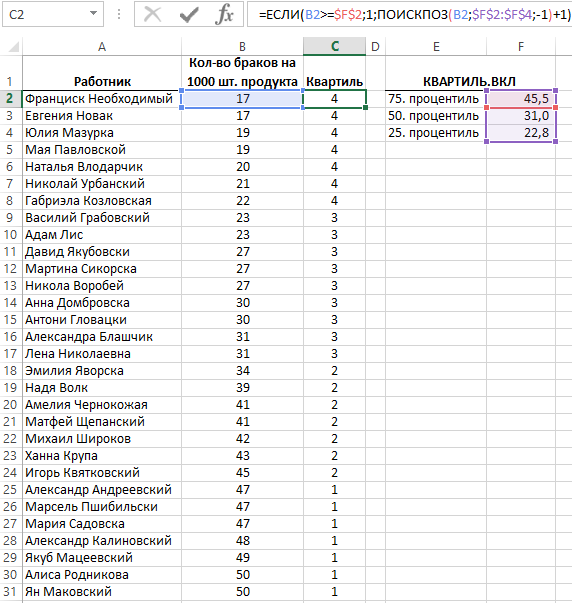
Ниже на рисунке отображаются данные обработанные новой функцией КВАРТИЛЬ.ИСКЛ:
Так же изменена формула определяющая номер квартиля для каждого исходного значения:
=$F$2;1;ПОИСКПОЗ(B2;$F$2:$F$4;-1)+1)’ >
Так как функция КВАРТИЛЬ.ИСКЛ не позволяет вычислять границы между квартилями с максимальными и минимальными значениями, была использована формула с функцией ЕСЛИ для проверки: является ли текущее значение большим от доли 75% – значение 3-го квартиля.
Как работает функция КВАРТИЛЬ в Excel
С целью поиска двух значений находящийся по первых сторонах границ квартиля функция КВАРТИЛЬ вычисляет процентную долю числа всех значений, уменьшенных на 1. После чего интерполирует найденные значения и таким образом возвращает итоговый результат своего вычисления.
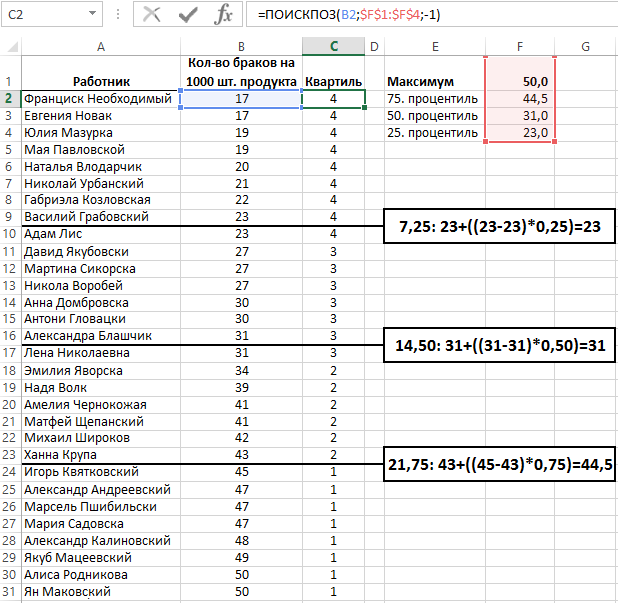
В одном из выше описанных примеров функция КВАРТИЛЬ выполняет математические операции 0,75*(30-1). Поэтому для числового значения 30 будет возвращен результат 21,75. Далее функция сортирует значения от наименьших до наибольших и отсчитывает 21-ну строку, начиная от наименьшего значения. Так как результат первой операции не является целым числом, функция выполняет интерполяцию для обоих найденных значений. В данном примере после отсчета 21-ой строки в направлении от меньшего к большему были найдены числовые значения 43, а следующее 45. В интерполяции было использовано дробное число 21,75 с целью нахождения значения составляющего 75 процентиля между числами 43 и 45, согласно формуле 43+((45-43)*0,75).
Подобным способом для квартиля 50, функция выполняет действие по алгоритму формулы: 0,5*(30-1), результат вычисления которой возвращает дробное число 14,5. Отсчитывая строки, начиная от наименьшего значения, граница припадает на строках Александра Блашчик / 31 и Лена Николаевна / 31. Так как оба значения равны между собой интерполяция будет простой и возвратит в результате число 31. На втором рисунке представлены те самые данные о работниках и браках, однако они для наглядности отсортированы и схематически указаны линии где проходят границы между квартилями.
Квантили распределений EXCEL
Медиана и квартили
Квантили нормального распределения
Математическое описание
Крайне важное определение: математическое ожидание – это площадь под графиком распределения. Если мы говорим о дискретном распределении – это сумма событий умноженных на соответсвующие вероятности, также известно как момент:
(2) E(X) = Σ(pi•Xi) E – от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:
(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)
Центральный момент степени k:
Среднее значение
Среднее значение (μ) закона распределения – это математическое ожидание случайной величины (случайная величина – это событие), например, сколько в среднем посетителей заходит в магазин в час:
| Кол-во посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество наблюдений | 114 | 115 | 52 | 52 | 24 | 13 | 30 |
| Таблица 1. Количество посетителей в час | |||||||
Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:
μ = (114 • 0 + 115 • 1 + 52 • 2 + 52 • 3 + 24 • 4 + 13 • 5 + 30 • 6) / 400 = 716/400 = 1.79
То же самое мы можем проделать используя формулу 2:
μ = M(X) = Σ(Xi•pi) = 0 • 0.29 + 1 • 0.29 + 2 • 0.13 + 3 • 0.13 + 4 • 0.06 + 5 • 0.03 + 6 • 0.08 = 1.79 Момент первой степени, формула (5)
Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 1.79 посетителя в час
| Количество посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятность (%) | 28.5 | 28.8 | 13 | 13 | 6 | 3.3 | 7.5 |
| Таблица 2. Закон распределения количества посетителей | |||||||
Отклонение от среднего
Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:
График 2. График функции вероятности. Распределение ≈ 100±5
Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы использовать в качестве меры удалённости “разность” между средним и случайными величинами:
но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц между величинами и средним значением:
Соответственно, среднее значение удалённости – это математическое ожидание квадратов удалённости:
(9) σ 2 = E[(X – E(X)) 2 ] Поскольку вероятности любой удалённости равносильны – вероятность каждого из них – 1/n, откуда: (10) σ 2 = E[(X – E(X)) 2 ] = ∑[(Xi – μ) 2 ]/n Она же формула центрального момента (6) второй степени
σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ 2 называется дисперсией. Корень из дисперсии называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:
Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:
Квантиль
График 3. Функция распределения. Медиана
График 4. Функция распределения. 4-квантиль или квартиль
График 5. Функция распределения. 0.34-квантиль
Для анализа функции распределения ввели понятие квантиль. Квантиль – это случайная величина при заданном уровне вероятности, т.е.: квантиль для уровня вероятности 50% – это случайная величина на графике плотности вероятности, которая имеет вероятность 50%. На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)
То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям, и для каждого дециля нашли значение случайной величины.
Также, используется обозначение x-квантиль, где х – дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при p = 0.34.
Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.
Построение интервалов
Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например, интерес – случайное число = 98), а для группы событий (например, интерес – случайное число между 96 и 99). Доверительный интервал бывает двух видов: односторонний и двусторонний. Параметр доверительного интервала – уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.
Двусторонний доверительный интервал
Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются “критическая область“
Первый квартиль
Значение квартиля Q1 находится в интервале 68,98 – 71,70, соответствующего частоте fQ1 = 150:4 = 37,5
Третий квартиль
Значение квартиля находится в интервале 68,98 – 71,70, соответствующего частоте fQ3 = (3*150):4 = 112,5
Квартили непрерывного распределения
Если функция распределения F (х) случайной величины х непрерывна, то 1-й квартиль является решением уравнения F(х) =0,25, второй – F(х) =0,5, а третий F(х) =0,75.
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ 2 ), получим, что медиана (2-й квартиль ) вычисляется по формуле e μ или в MS EXCEL =EXP(μ). При μ=1, медиана равна 2,718.
Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице:
Поэтому, линии квартилей ( х=квартиль ) делят площадь под графиком функции плотности вероятности на 4 равные части.
Квартили в MS EXCEL
Моменты случайной величины
Моменты случайно величины описывают различные аспекты характера и формы нашего распределения.
#1 — первый момент случайной величины — среднее значение данных, которое показывает место распределения.
#2 — второй момент случайной величины — дисперсия, которая показывает разброс распределения. Большие значения имеют больший размах, чем маленькие.
#3 — третий момент случайной величины — коэффициент асимметрии — мера того, насколько неравномерным является распределение. Коэффициент асимметрии положителен, если распределение наклонено влево и левый хвост короче правого. То есть среднее значение находится правее. И наоборот:
#4 — четвертый момент случайной величины — коэффициент эксцесса, который описывает то, насколько толстый хвост и насколько острый пик распределения. Этот коэффициент показывает, насколько вероятно найти точки экстремума в данных. Чем выше значение, тем вероятнее выбросы. Это похоже на разброс (дисперсию), но между ними есть отличия.
Как видно на графике, чем выше значение пики, тем выше коэффициент эксцесса, т.е. у верхней кривой коэффициент эксцесса выше, чем у нижней.
Статистический анализ роста доли дохода в Excel за период
Пример 2. В таблице приведены данные о доходах предпринимателя за год. Доказать, что примерно 75% значений меньше, чем третий квартиль доходов.
Вид исходной таблицы:
Определим 3-й по формуле:

Определим соотношение чисел, меньше полученного числа, к общему количеству значений по формуле:
=СЧЁТЕСЛИ(B2:B13;” Пример 3. Имеется диапазон случайных чисел, отсортированный в порядке возрастания. Определить соотношение суммы чисел, которые меньше 1-го квартиля, к сумме чисел, которые превышают значение 1-го квартиля.
Чтобы сгенерировать случайное число в Excel воспользуемся функцией:
После генерации отсортируем случайно сгенерированные числа по возрастанию. Вид исходной таблицы данных со случайными числами:
Формула для расчета имеет следующий вид (формула массива CTRL+SHIFT+ENTER):
Функции СУММ с вложенными функциями ЕСЛИ выполняют расчет суммы только тех чисел, которые меньше и больше соответственно значения, возвращаемого функцией для исследуемого диапазона. Из полученных значений вычисляется частное. Результат расчетов:
Общая сумма чисел исследуемого диапазона, которые меньше 1-го квартиля, составляет всего 8,57% от общей суммы чисел, которые больше 1-го квартиля.
Расчет квартилей в R и SAS
Функция quantile в R использует все девять алгоритмов расчета квантилей, в соответствии с нумерацией, предложенной Hyndman and Fan в работе 1996 г. (рис. 15; если вы не знакомы с R, рекомендую начать с Алексей Шипунов. Наглядная статистика. Используем R! ). Квантиль при i-м методе расчета:
Расчет децилей для дискретного ряда
Определяем номер дециля по формуле: 
Если номер дециля – целое число, то значение дециля будет равно величине элемента ряда, которое обладает накопленной частотой равной номеру дециля. Например, если номер дециля равен 20, его значение будет равно значению признака с S =20 (накопленной частотой равной 20).
Если номер дециля – нецелое число, то дециль попадает между двумя наблюдениями. Значением дециля будет сумма, состоящая из значения элемента, для которого накопленная частота равна целому значению номера дециля, и указанной части (нецелая часть номера дециля) разности между значением этого элемента и значением следующего элемента.
Например, если номер дециля равна 20,25, дециль попадает между 20-м и 21-м наблюдениями, и его значение будет равно значению 20-го наблюдения плюс 1/4 разности между значением 20-го и 21-го наблюдений.
Квантили специальных видов
Часто используются Квантили специальных видов:
В качестве примера вычислим медиану (0,5-квантиль) логнормального распределения LnN(0;1) (см. файл примера лист Медиана ).
Это можно сделать с помощью формулы =ЛОГНОРМ.ОБР(0,5; 0; 1)
Квантили стандартного нормального распределения
Необходимость в вычислении квантилей стандартного нормального распределения возникает при проверке статистических гипотез и при построении доверительных интервалов.
В данных задачах часто используется специальная терминология:
Однако, при проверке гипотез и построении доверительных интервалов чаще используется “верхний” α-квантиль. Покажем почему.
Верхним α – квантилем называют такое значение x α , для которого вероятность, того что случайная величина X примет значение больше или равное x α равна альфа: P(X>= x α )= α . Из определения понятно, что верхний альфа – квантиль любого распределения равен нижнему (1- α) – квантилю. А для распределений, у которых функция плотности распределения является четной функцией, верхний α – квантиль равен нижнему α – квантилю со знаком минус . Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.
Действительно, для α=0,05, верхний 0,05-квантиль стандартного нормального распределения равен 1,645. Т.к. функция плотности вероятности стандартного нормального распределения является четной функцией, то вычисления в MS EXCEL верхнего квантиля можно сделать по двум формулам:
Чтобы пояснить название « верхний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения для α=0,05.
Вычислить двусторонний 0,05 – квантиль это можно с помощью формул MS EXCEL: =НОРМ.СТ.ОБР(1-0,05/2) или =-НОРМ.СТ.ОБР(0,05/2)
Другими словами, двусторонние α-квантили задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.
Квантили распределения Стьюдента
Чтобы вычислить в MS EXCEL верхний 0,05/2 – квантиль для t-распределения с 10 степенями свободы (или тоже самое двусторонний 0,05-квантиль ), необходимо записать формулу =СТЬЮДЕНТ.ОБР.2Х(0,05; 10) или =СТЬЮДРАСПОБР(0,05; 10) или =СТЬЮДЕНТ.ОБР(1-0,05/2; 10) или =-СТЬЮДЕНТ.ОБР(0,05/2; 10)
Квантили распределения ХИ-квадрат
Вычислять квантили распределения ХИ-квадрат с n -1 степенью свободы требуется, если проводится проверка гипотезы о дисперсии нормального распределения (см. статью Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения ).
Чтобы вычислить верхний 0,05/2 – квантиль для ХИ 2 -распределения с числом степеней свободы 10, т.е. χ 2 0,05/2,n-1 , необходимо в MS EXCEL записать формулу =ХИ2.ОБР.ПХ(0,05/2; 10) или =ХИ2.ОБР(1-0,05/2; 10)