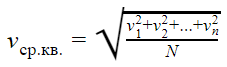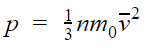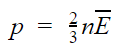Как посчитать среднюю квадратичную скорость
Формула средней квадратичной скорости молекул газа идеального. Пример задачи
Молекулярно-кинетическая теория позволяет, анализируя микроскопическое поведение системы и используя методы статистической механики, получить важные макроскопические характеристики термодинамической системы. Одной из микроскопических характеристик, которая связана с температурой системы, является средняя квадратичная скорость молекул газа. Формулу для нее приведем и рассмотрим в статье.
Газ идеальный
Сразу отметим, что формула квадратичной средней скорости молекул газа будет приведена именно для газа идеального. Под ним в физике полагают такую многочастичную систему, в которой частицы (атомы, молекулы) не взаимодействуют друг с другом (их кинетическая энергия на несколько порядков превышает потенциальную энергию взаимодействия) и не имеют размеров, то есть являются точками с конечной массой (расстояние между частицами на несколько порядков превышает их размеры линейные).
Теория молекулярно-кинетическая (МКТ)
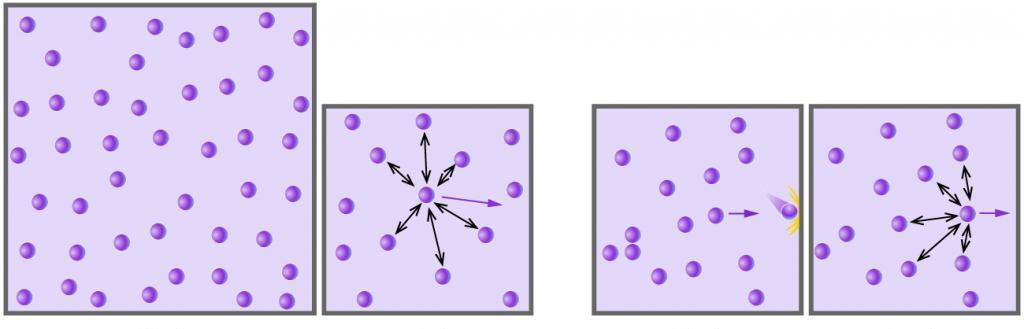
Изучая идеальный газ в рамках МКТ, следует обратить внимание на два важных процесса:
Несмотря на то, что индивидуальные скорости газовых частиц сильно отличаются друг от друга, среднее значение этой величины сохраняется постоянным во времени, если отсутствуют внешние воздействия на систему. Формулу средней квадратичной скорости молекул газа можно получить, если рассмотреть связь между кинетической энергией и температурой. Займемся этим вопросом в следующем пункте статьи.
Вывод формулы квадратичной средней скорости молекул газа идеального
Каждый школьник знает из общего курса физики, что кинетическая энергия поступательного движения тела массой m рассчитывается так:
Приравнивая оба равенства и выражая из них v, получим формулу средней скорости квадратичной газа идеального:
Величина M определяется так:
Принимая во внимание оба равенства, получаем следующее выражение для средней квадратичной скорости молекул:
Таким образом, средняя квадратичная скорость газовых частиц оказывается прямо пропорциональной квадратному корню из абсолютной температуры и обратно пропорциональна корню квадратному из молярной массы.
Пример решения задачи
Каждый знает, что воздух, которым мы дышим, на 99% состоит из азота и кислорода. Необходимо определить разницы в средних скоростях молекул N2 и O2 при температуре 15 oC.
Эту задачу будет решать последовательно. Сначала переведем температуру в абсолютные единицы, имеем:
T = 273,15 + 15 = 288,15 К.
Теперь выпишем молярные массы для каждой рассматриваемой молекулы:
Поскольку значения молярных масс отличаются между собой незначительно, то средние их скорости при одинаковой температуре тоже должны быть близки. Пользуясь формулой для v, получаем следующие значения для молекул азота и кислорода:
v (N2) = √(3*8,314*288,15/0,028) = 506,6 м/с;
v (O2) = √(3*8,314*288,15/0,032) = 473,9 м/с.
Поскольку молекулы азота немного легче, чем молекулы кислорода, то движутся они быстрее. Разница средних скоростей составляет:
Полученное значение составляет всего 6,5 % от средней скорости молекул азота. Обращаем внимание на большие значения скоростей молекул в газах даже при невысоких температурах.
Средняя скорость молекул
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
» open=» υ k υ = 1 N ∑ i = 1 N υ i 2
Формулу средней квадратичной скорости можно переписать так:
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
» open=» υ k υ = 3 k T m 0 = 3 R T μ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
где n = N V – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
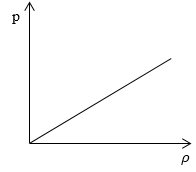
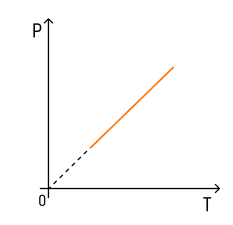
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1 ).
Запишем выражение для средней скорости движения молекул газа следующим образом:
» open=» υ = 8 k T πm 0
Из графика видно, что p
» open=» υ = 8 k T πm 0 = 8 C ρ π n n ρ = 8 C π
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Применим выражение для » open=» υ k υ :
» open=» υ k υ = 3 R T μ
Помимо этого, из уравнения Менделеева-Клайперона и зная, что m μ = N N A :
p = n N A R T → R T = p N A n
» open=» υ k υ = 3 p N A μ n
Определение средней квадратичной скорости молекул газа
Средняя квадратичная скорость молекул газа — что это за параметр
Молекулы любого газа пребывают в постоянном движении. Его можно охарактеризовать с точки зрения средней их скорости или средней квадратичной скорости. Первое понятие имеет специальный термин — скорость теплового движения. Второе — средняя квадратичная скорость — величина, для которой существует специальная формула.
Для того, чтобы полностью разобраться в понятии средней квадратичной скорости молекул газа, вводится условный участник процесса — идеальный газ.
Идеальный газ — это математическая модель, потенциальную энергию которой принимают за ноль, а кинетическую характеризуют в полном объеме. Идеальный газ подходит в качестве модели окружающих нас газов, например, обычного воздуха.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Средняя квадратичная скорость — физическая величина, отличная от средней арифметической скорости молекул, определяемая по формуле: корень квадратный из средней арифметической квадратов скоростей различных молекул.
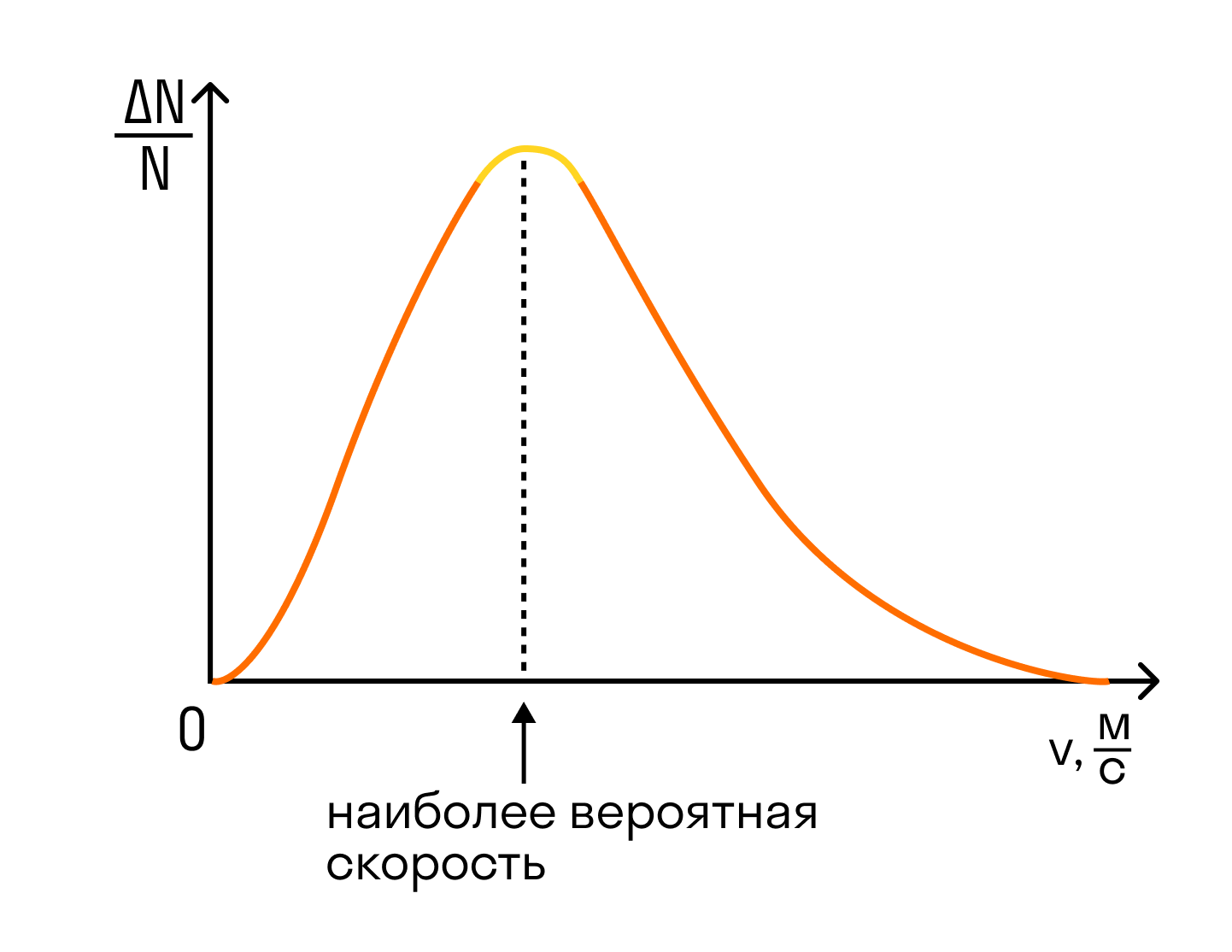
Кинетическая энергия определяется скоростью движения молекул, поэтому зависит от температуры. Скорости молекул одного газа не одинаковы. Часть молекул движутся очень быстро, часть — с незначительной скоростью. Однако для большинства существует некое среднее значение. Если изобразить это на графике в виде параболы, такие молекулы со средней скоростью будут составлять ее верхнюю часть.
В единице объема газа содержится огромное число молекул. Поэтому, например, его давление на стенки сосуда — величина постоянная. В ином случае, если бы в единицу времени о стенку ударялось различное количество молекул, давление бы «скакало».
Из изложенного можно сделать вывод: скорость — свойство отдельной молекулы газа, а давление — характеристика их совокупности.
От каких величин зависит в идеальном газе
Для идеального газа средняя квадратичная скорость прямо пропорциональна его температуре и обратно пропорциональна молярной массе газа.
В математическом выражении данная зависимость выражается через корень квадратный:
где R — универсальная постоянная величина, Т — температура газа, μ — молярная масса.
Из формулы видно, что искомая величина (средняя квадратичная скорость) зависит от природных свойств газа и его температуры.
Формула средней квадратичной скорости молекул
Математическое выражение формулы выглядит следующим образом:
В формуле присутствуют следующие условные обозначения: V1, V2, Vn — скорости молекул, а N — их количество.
Формула может иметь и другой вид:
Как посчитать в зависимости от природы газа и температуры?
Проведенное интегрирование формулы, цель которого определить зависимость искомой единицы от природных свойств иттемпературы газа, приводит расчеты к формуле:
При поступательном движении молекул газа Vср кв — составляющая уравнения для молекулярно-кинетической теории.
Если n=N/V, где N — число частиц, а V — объем, то концентрация частиц n получает следующее формульное выражение:
Средняя квадратичная скорость молекул

Всего получено оценок: 84.
Всего получено оценок: 84.
Температура — это уровень внутренней энергии, заключённой в хаотическом движении молекул вещества. Скорость конкретной молекулы может иметь весьма широкий диапазон, однако скорость большинства молекул лежит в достаточно узких пределах, поэтому в молекулярной физике используется среднее значение этой скорости. Как же оно определяется?
Среднее значение физической величины
Большинство физических величин, характеризующих конкретный объект, имеет вполне определённое значение. Однако, если рассматривается несколько объектов, измеренная величина может быть различна для каждого объекта. И для моделирования поведения системы этих объектов требуется учитывать все значения.
С возрастанием числа объектов измерять параметры для каждого объекта становится всё сложнее. Но при этом зачастую оказывается, что все измеряемые значения лежат в некоторых пределах, причём систему можно достаточно точно моделировать, пренебрегая мелкими отличиями параметров каждого объекта.
Когда число объектов очень велико (например, число молекул в теле), этот метод является единственно возможным. Более того, значение, полученное для одного конкретного объекта, практически не играет роли.
В таких случаях используется специальное значение, при котором суммарная ошибка параметра для всех объектов будет наименьшей. Это значение называется средним значением физической величины. Среднее значение может рассчитываться несколькими способами.
Скорость молекул газа
Газ — это хороший пример системы, которая состоит из большого числа движущихся объектов (молекул), при этом скорость каждой отдельной молекулы не имеет значения, и единственный способ оценки молекулярных движений — использование средней скорости.
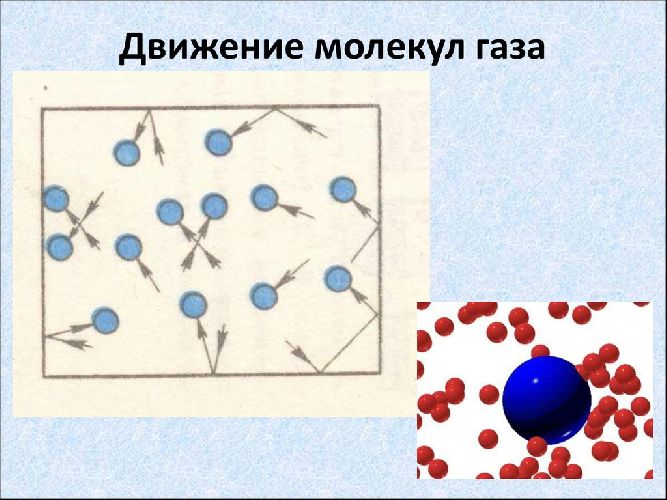
Простейший способ нахождения среднего значения — это суммирование всех значений и деление суммы на количество значений. Такое среднее называется средним арифметическим.
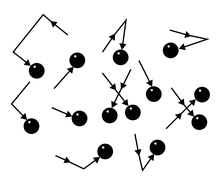
Для скорости молекул такое среднее не подходит. Скорости молекул имеют самые разные направления, и, какое бы направление мы не взяли, всегда окажется, что по этому направлению и против него движется одинаковое число молекул. Простая сумма скоростей будет равна нулю. Поэтому здесь используется среднее значение квадрата скорости молекул.
Особенности среднеквадратичного значения
Квадрат любого ненулевого числа положителен, поэтому значение в приведённой формуле также всегда будет положительным.
Ещё одно преимущество использования средней квадратичной скорости молекул состоит в том, что кинетическая энергия материальной точки находится по формуле:
Получается, что средняя квадратичная скорость молекул газа удобна для нахождения средней энергии молекулы, а она, в свою очередь, связана с макроскопическими параметрами — с температурой и давлением. Поэтому именно среднеквадратичная скорость используется в большинстве формул молекулярно-кинетической теории.

Что мы узнали?
Средняя квадратичная скорость молекул газа — удобный показатель, широко использующийся в молекулярно-кинетической теории для определения макроскопических параметров — температуры и давления.
Идеальный газ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Газ: агрегатное состояние
У веществ есть три агрегатных состояния — твердое, жидкое и газообразное.
Их характеристики — в таблице:
Агрегатные состояния
Свойства
Расположение молекул
Расстояние между молекулами
Движение молекулы
Твердое
сохраняет форму и объем
в кристаллической решетке
соотносится с размером молекул
колеблется около положения в кристаллической решетке
Жидкое
близко друг к другу
молекулы малоподвижны, при нагревании скорость движения увеличивается
Газообразное
занимает предоставленный объем
больше размеров молекул
хаотичное и непрерывное
В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.
Агрегатных состояний точно три?
На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Модель идеального газа
В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.
Идеальный газ — это модель реального газа. Молекулы идеального газа представляют собой материальные точки, которые не взаимодействуют друг с другом на расстоянии, но взаимодействуют при столкновениях друг с другом или со стенками сосуда. При работе с идеальным газом можно пренебречь потенциальной энергией молекул (но не кинетической).
В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.
Свойства идеального газа
Среднеквадратичная скорость
Потенциальной энергией молекул газа пренебречь можно, а вот кинетической — никак нельзя. Потому что кинетическая энергия — это энергия движения, а мы не можем пренебрегать скоростью движения молекул.
На графике показано распределение Максвелла — то, как молекулы распределяются по скоростям. Судя по графику, большинство молекул движутся со средним значением скорости. Хотя есть и быстрые, и медленные молекулы, просто их значительно меньше.
Но наш газ идеальный, а в идеальном газе случаются чудеса. Одно из таких чудес — то, что все молекулы идеального газа двигаются с одинаковой скоростью. Эта скорость называется средней квадратичной.
Средняя квадратичная скорость
v1, v2, vn — скорости разных молекул [м/с]
N — количество молекул [-]
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Давление идеального газа
Молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.
Например, в комнате, в которой вы сейчас находитесь, за одну секунду на каждый квадратный сантиметр молекулы воздуха наносят столько ударов, что их количество выражается двадцатитрехзначным числом.
Хотя сила удара отдельной молекулы мала, действие всех молекул на стенки сосуда приводит к значительному давлению. Представьте, что комар пытается толкать машину — она не сдвинется с места. Но если за работу возьмется пара сотен миллионов комаров, то машину получится сдвинуть.
Эксперимент
Чтобы смоделировать давление газа, возьмите песок и лист бумаги, зажатый между двумя книгами. Песчинки будут выступать в роли молекул газа, а лист — в роли сосуда, в котором этот газ находится. Когда вы начинаете сыпать песок на лист бумаги, бумага отклоняется под воздействием множества песчинок. Так же и молекулы газа оказывают давление на стенки сосуда, в котором находятся.
Зависимость давления от других величин
Зависимость давления от объема
В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.
Давление
p = F/S
F — сила [Н]
S — площадь [м2]
То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.
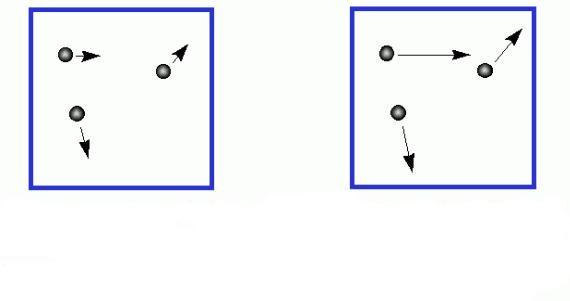
Рассмотрим аналогичный пример с двумя сосудами разной площади.
Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.
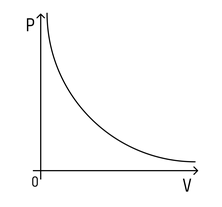
При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):
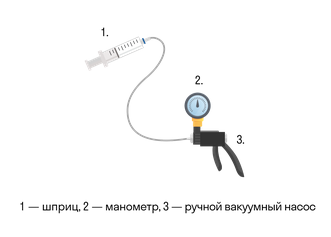
Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:
Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.
Зависимость давления от температуры
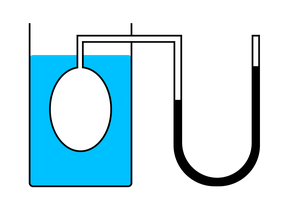
Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.
В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.
Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.
Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.
С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:
Эта зависимость называется законом Шарля в честь ученого, открывшего ее.
Основное уравнение МКТ
Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.
В основе молекулярно-кинетической теории лежат три положения.
Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.
Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.
Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.
Основное уравнение МКТ
p = nkT
p — давление газа [Па]
T — температура газа [К]
m 0 — масса одной молекулы [кг]
v — средняя квадратичная скорость [м/с]
Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.
Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v2, а вместо v— и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.
Мы знаем, что кинетическая энергия вычисляется по следующей формуле:
Кинетическая энергия
Ек = mv 2 /2
Ек — кинетическая энергия [Дж]
m — масса тела [кг]
v — скорость [м/с]
Для молекулы газа формула примет вид:
Средняя кинетическая энергия поступательного движения молекулы
Ек — средняя кинетическая энергия поступательного движения молекулы [Дж]
m0 — масса молекулы [кг]
v — скорость молекулы [м/с]
Из этой формулы можно выразить m0v 2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Основное уравнение МКТ
p — давление газа [Па]
n — концентрация [м-3]
E — средняя кинетическая энергия поступательного движения молекулы [Дж]
Хранение и транспортировка газов
Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.
Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.
Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.