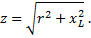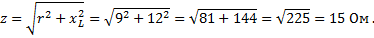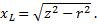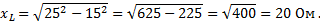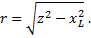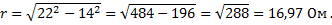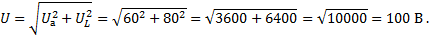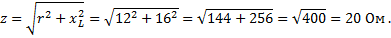Как посчитать сопротивление в треугольнике

Физический портал для школьников и абитуриентов

Вы здесь

Подготовка к олимпиаде. Методы расчета резисторных схем постоянного тока. 3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»

Методы расчета резисторных схем постоянного тока

3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»

Рассматриваемый метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым. Однако, поскольку в результате такого преобразования изменяются токи внутри цепи, такую замену можно проводить только в тех случаях, когда не надо находить распределение токов.

Подобные преобразования широко известны для случая двух выводов. Так, например, два резистора сопротивлениями R₁ и R₂, включенные последовательно, можно заменить одним резистором сопротивлением R₁ + R₂. Если резисторы включены параллельно, то их можно заменить одним резистором сопротивлением

И в этих случаях распределение токов в цепи (или в части цепи) претерпевает изменения. Рассмотрим более сложное преобразование схем, имеющих три вывода (трехполюсников). Иначе это называется преобразованием «звезды» (рис. а) в «треугольник» (рис. б), и наоборот.

Сопротивления резисторов в схеме «звезда» обозначаются с индексом точки, с которой соединен этот резистор, например, резистор r₁ соединен с точкой 1. В «треугольнике» индексы резисторов соответствуют точкам, между которыми они включены, например, резистор R₁₃ подключен к точкам 1 и 3. Как отмечено выше, чтобы заменить одну из этих схем другой, нужно получить такие соотношения между их сопротивлениями, чтобы эквивалентные сопротивления между любыми точками были одинаковы для обеих схем (при условии сохранения числа этих точек). Так, в «звезде» сопротивление между точками 1 и 2 равно r₁ + r₂, в «треугольнике»

следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы выполнялось следующее равенство:

Аналогично для точек 2 и 3 и для точек 1 и 3:

Сложим все эти уравнения и, поделив обе части на 2, получим:

Вычитая из этого уравнения поочередно предыдущие, получим:

Эти выражения легко запомнить:

знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева:

$r_1 \rightarrow R_<12>R_<13>, r_2 \rightarrow R_<12>R_<23>, r_3 \rightarrow R_<13>R_<23>$.

Аналогично получают и формулы обратного преобразования:

Последние выражения также легко запомнить и проверить:

числитель у всех уравнений один и тот же, а в знаменателе стоит сопротивление резистора с индексом, которого не достает в левой части выражения.

Этот метод представляет собой наиболее универсальный подход к решению практически всех типов задач на разветвленные цепи.

Задача 27. Определите сопротивление цепи АВ (рис.), если R₁ = R₅ = 1 Ом, R₂ = R₆ = 2 Ом, R₃ = R₇ = 3 Ом, R₄ = R₈ = 4 Ом.

Решение. Преобразуем «треугольники» R₁R₂R₈ и R₄R₅R₆ в эквивалентные «звезды». Схема примет иной вид (рис.).

Теперь нет никаких препятствий для расчета схемы, которая состоит из последовательно и параллельно соединенных резисторов (рис.). После простых расчетов получим

Источник

Треугольник сопротивлений

Если стороны треугольника напряжений (рисунок 1, а) разделить на ток I (рисунок 1, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому – треугольник сопротивлений (рисунок 1, в).

Рисунок 1. Получение треугольника сопротивлений

В треугольнике сопротивления, показанном отдельно на рисунке 2, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного r и индуктивного x_L сопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

Если одно из сопротивлений цепи (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко можно убедиться непосредственным расчетом.

Пример 1. Определить полное сопротивление цепи, в которой r = 9 Ом и x_L = 12 Ом.

Было бы совершенно неправильно, если бы для определенного полного сопротивления были арифметически сложены оба сопротивления r и x_L, так как

Результат, как мы видим, в этом случае получается неверный.

Пример 2. Полное сопротивление обмотки электромагнита z = 25 Ом. Активное сопротивление обмотки r = 15 Ом. Определить индуктивное сопротивление.

Пример 3. Индуктивное сопротивление обмотки электродвигателя переменного тока равно 14 Ом. Полное сопротивление ее равно 22 Ом. Найти активное сопротивление.

Пример 4. В цепи, изображенной на рисунке 3, определить показание вольтметра.

Рисунок 3. К примеру 4

Определим общее сопротивление:

Если умножить z на ток I, получим:

то есть тот же результат, что и выше.

Источник

№7 Эквивалентное преобразование треугольника и звезды сопротивлений.

Пусть требуется рассчитать цепь, показанную на рис. 7.1, а.

Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.

Треугольник и звезда сопротивлений имеют вид, показанный на рис. 7.2.

Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.

Можно показать, что условием эквивалентности являются следующие уравнения:

а) при преобразовании треугольника в звезду:

б) при преобразовании звузды в треугольник:

Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.

При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R3.

Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.

а) Решение преобразованием треугольника в звезду.

Теперь общее сопротивление цепи легко находится:

Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен:

Токи в паралельных ветвях:

Возвращаемся к исходной схеме (рис. 7.1, а):

Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A. Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.

б) Решение преобразованием звезды в треугольник.

Преобразуем звезду, образуемую в схеме на рис. 7.1, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 7.1, в).

Определяем сопротивления треугольника:

Теперь рассчитываем преобразованную цепь. Сначала находим эквивалентные сопротивления участков ac и cd:

Затем определяем общее сопротивление и токи:

Возвращаемся к исходной схеме:

Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.

Источник

Преобразование треугольник/звезда: что за сценой?

Преобразования треугольник/звезда позволяют нам заменить часть схемы другой схемой, которая, хотя и эквивалентна в поведении, но может значительно упростить анализ общей схемы. Здесь мы узнаем, откуда берутся эти преобразования.

Зачем?

Но теперь мы подошли к схемам (рисунок 2), где нет никаких пар резисторов, которые включены последовательно или параллельно, – похоже, мы зашли в тупик. Одним из способов анализа этой схемы является использование закона напряжений Кирхгофа (второй закон) и закона токов Кирхгофа (первый закон) для получения алгебраических уравнений, которые мы можем решить для напряжений и токов. Хотя этот подход будет работать всегда (для этой и большинства других типов схем), он может быть довольно громоздким. Мы могли бы смириться с этим как с ценой возможности анализа этих более сложных схем, но иногда мы можем избежать оплаты этого счета, изменяя или «преобразовывая» фрагменты схемы, чтобы превратить ее в нечто, что мы можем уменьшить, используя только правила последовательного/параллельного объединения.

Для простоты мы будем рассматривать только цепи постоянного тока с резисторами, но эти принципы применимы к любой линейной системе переменного или постоянного тока. Кроме того, чтобы сфокусировать обсуждение на преобразованиях, мы найдем только общий ток, поставляемый источником напряжения, что означает, что мы стремимся свести всю сеть резисторов в единое эквивалентное сопротивление.

Давайте рассмотрим эти две схемы немного подробнее (рисунок 3). Мы видим, что единственная разница между ними заключается в том, что находится внутри пунктирных окружностей. В каждом случае цепь в окружности имеет три контакта, которые пересекают окружность для взаимодействия с остальной частью схемы. В левой цепи (рисунок 3(a)) резисторы подключены к контактам в конфигурации «треугольник» (в англоязычной литературе, конфигурация «delta», «дельта», названная в честь заглавной греческой буквы Δ). А в правой цепи резисторы подключены в конфигурации «звезда» (в англоязычной литературе, конфигурация «wye», «уай», названная в честь заглавной английской буквы Y, хотя в схеме она перевернута).

Теперь представьте, что резисторы внутри пунктирной окружности в левой цепи помещены в черный ящик, этот ящик удален из схемы и заменен другим черным ящиком, который заставляет схему вести себя точно так же. Далее представьте, что, когда вы открываете, этот новый ящик он содержит три резистора, расположенных как в правой цепи. Кто бы ни придумал второй черный ящик, он очень тщательно выбрал значения резисторов так, чтобы эти два блока были неразличимы для остальной части схемы: мы знаем, как анализировать правую схему, и теперь мы знаем, что когда мы это делаем, результаты можно применить к левой схеме, потому что они эквивалентны. Вот зачем выполнять преобразования «треугольник→звезда» и «звезда→треугольник».

Основные соотношения

Чтобы определить уравнения, связывающие резисторы в цепи, соединенной треугольником, с резисторами в цепи, соединенной звездой, нам ничего не нужно, кроме наших надежных формул для последовательных/параллельных соединений (и немного алгебры). Идея заключается в выравнивании эквивалентных сопротивлений между соответствующими парами контактов при отключенном оставшемся контакте (рисунок 4)

Выполнив это для эквивалентного сопротивления между контактами B-C, мы получим:

\[R_B + R_C = \frac \left( R_ + R_ \right) > + R_ + R_>\]

Если мы повторим этот процесс для каждой другой пары контактов по очереди, мы получим еще два аналогичных уравнения, и любое из них даст нам необходимую нам информацию (при условии, что мы распознаем задействованную симметрию).

Частный случай: симметричные схемы

Если сопротивления в каждом плече цепи, соединенной треугольником или звездой, равны, такая цепь считается «симметричной». Это означает, что

\[R_Y = R_A = R_B = R_C\]

Комбинация этого условия с соотношением из предыдущего раздела сразу приводит к уравнению преобразования для случая симметрии.

Это гораздо более значительный результат, чем может показаться на первый взгляд, и причина довольно проста – когда инженеры проектируют схемы с соединениями треугольник или звезда, они часто стараются сделать эти схемы симметричными. Хотя, конечно, это не всегда возможно, и поэтому мы должны иметь возможность разобраться с общим случаем, когда схема не симметрична.

Общий случай преобразования треугольник→звезда

Поскольку у нас есть три неизвестных, нам нужно еще два уравнения. Они получаются из эквивалентных сопротивлений, видимых при рассмотрении двух других пар контактов. Выполнив это (или используя симметрию) мы получаем

Сложив эти два уравнения вместе и вычтя наше первое уравнение, мы получим

Мы можем решить систему уравнению для двух других неизвестных сопротивлений (или использовать симметрию), чтобы получить

Эти отношения могут быть обобщены очень компактно. Сопротивление, подключенное к каждому узлу в эквивалентной цепи, соединенной звездой, равно произведению сопротивлений, подключенных к соответствующему узлу в цепи, соединенной треугольником, деленному на сумму сопротивлений всех резисторов в треугольнике. Обычно это выражается формулой, такой как

Общий случай преобразования звезда→треугольник

Другими словами, отношение сопротивлений резисторов, подключенных к любым двум контактам в схеме звезда, равно отношению сопротивлений резисторов, соединяющих те же самые два контакта с третьим контактом в схеме треугольник. Следовательно, два других соотношения будут следующими

Вооружившись этим, мы могли бы вернуться к нашим основным соотношениям и продолжить работу с ними, но в качестве отправной точки проще использовать одно из отношений из общего случая преобразования треугольник→звезда.

\[R_ = R_A \left( \over R_> + \over R_ > + 1 \right)\]

Два других выражения получаются аналогично (или согласно симметрии):

Эти выражения могут быть обобщены очень компактно. Сопротивление, подключенное между каждой парой узлов в эквивалентной схеме, соединенной треугольником, равно сумме сопротивлений двух резисторов, подключенных к соответствующим узлам в схеме, соединенной звездой, плюс произведение сопротивлений этих двух резисторов, деленное на сопротивление третьего резистора.

Общий способ выразить это состоит в том, чтобы поместить правую часть под общим знаменателем, а затем отметить, что числитель в каждом выражении является суммой произведений каждой пары сопротивлений в цепи, соединенной звездой, а знаменатель – это сопротивление, подключенное к третьему контакту.

\[R_P = R_A R_B + R_B R_C + R_A R_C\]

Пример

Давайте поработаем с задачей, показанной на рисунке 5. Прежде чем мы начнем, давайте определим ожидаемый ответ, чтобы у нас была хорошая проверка того, является ли наш окончательный ответ правильным. Для этого рассмотрим роль мостового резистора 150 Ом. Этот резистор служит для уменьшения общего сопротивления, обеспечивая путь между левой и правой сторонами цепи. Следовательно, самое высокое эффективное сопротивление будет иметь место, если этот резистор будет удален полностью, и в этом случае полное сопротивление будет равно параллельной комбинации левой и правой сторон, что приведет к

С другой стороны, наименьшее общее сопротивление было бы получено путем уменьшения мостового резистора до прямого короткого замыкания, и в этом случае общее сопротивление было бы равно параллельной комбинации двух верхних резисторов, включенной последовательно с параллельной комбинацией двух нижних резисторов, что приведет к

Теперь мы ЗНАЕМ, что наш ответ ДОЛЖЕН быть между этими двумя предельными значениями. Во многих случаях простой анализ границ, такой как этот, приводит к ответу, который «достаточно хорошо» подходит для данной цели, но давайте предположим, что это не так. Используя приведенные выше уравнения преобразования треугольник→звезда, мы сначала определяем сумму сопротивлений резисторов треугольника.

Теперь, когда у нас есть все сопротивления для эквивалентной схемы звезда, мы можем очень легко определить общее сопротивление.

Поскольку это значение находится между нашими минимальной и максимальной границами, мы полностью уверены, что это правильный ответ, или, даже если мы допустили ошибку, наш ответ довольно близок к правильному. Поэтому суммарный ток равен

Заключение

Теперь мы увидели, что преобразования треугольник/звезда полезны, и, что более важно, увидели, как их можно легко выполнить, используя не более чем концепцию эквивалентных сопротивлений с использованием последовательных/параллельных комбинаций резисторов. Это может хорошо вам помочь, поскольку дает вам возможность вывести эти формулы на лету, если когда-нибудь возникнет в них необходимость, и у вас не будет подходящего справочного материала. Но что еще более важно, это должно служить для более прочного закрепления фундаментальных понятий в наборе инструментов, который хранится у вас в голове, позволяя вам использовать в своей работе еще более эффективные навыки анализа цепей.

В конце мы должны принять к сведению распространенное заблуждение, заключающееся в том, что преобразования треугольник↔звезда являются ЕДИНСТВЕННЫМ способом анализа цепей, которые нельзя уменьшить другими способами. В действительности, хотя эти преобразования могут сделать нашу жизнь проще, они не обязательны, поскольку ЛЮБОЙ контур, который можно проанализировать с их помощью, также можно проанализировать с помощью правил Кирхгофа, либо напрямую, либо с помощью одного из более формализованных методов их применения, включая метод контурных токов или метод узловых напряжений, а также с методиками, такими как эквивалентная схема Тевенина.

Источник

Как посчитать сопротивление в треугольнике

Преобразования треугольник-звезда и звезда-треугольник

Во многих схемах можно встретить такие конфигурации компонентов, в которых невозможно выделить последовательные или параллельные цепи. К этим конфигурациям относятся соединения компонентов в виде звезды (Y) и треугольника (Δ):

Очень часто, в ходе анализа электрических цепей, оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически, чаще возникает необходимость преобразования треугольника в звезду. Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. Иными словами, эквивалентные Δ и Y цепи ведут себя одинаково.

Существует несколько уравнений, используемых для преобразования одной цепи в другую:

Δ и Y цепи очень часто встречаются в 3-фазных сетях переменного тока, но там они, как правило, сбалансированы (все резисторы равны по значению) и преобразование одной цепи в другую не требует таких сложных расчетов. Тогда возникает вопрос: где мы сможем использовать эти уравнения?

Использовать их можно в несбалансированных мостовых схемах:

Анализ данной схемы при помощи Метода Токов Ветвей или Метода Контурных Токов довольно сложен. Теорема Миллмана и Теорема Наложения здесь тоже не помощники, так как в схеме имеется только один источник питания. Можно было бы использовать теорему Тевенина или Нортона, выбрав в качестве нагрузки резистор R₃, но и здесь у нас вряд ли что-нибудь получится.

После преобразования схема примет следующий вид:

В результате преобразования у нас получилась простая последовательно-параллельная цепь. Если мы правильно выполним расчеты, то напряжения между точками А, В и С преобразованной схемы будут аналогичны напряжениям между этими же точками исходной схемы, и мы сможем вернуть их обратно.

Сопротивления резисторов R₄ и R₅ остаются неизменными: 18 и 12 Ом соответственно. Применив к схеме последовательно-параллельный анализ, мы получим следующие значения:

Теперь, используя значения напряжений из приведенной выше таблицы, нам нужно рассчитать напряжения между точками А, В и С. Для этого мы применим обычную математическую операцию сложения (или вычитания для напряжения между точками В и С):

Переносим эти напряжения в исходную схему (между точками А, В и С):

Напряжение на резисторах R₄ и R₅ останется таким же, каким оно было в преобразованной схеме.

К данному моменту у нас есть все необходимые данные для определения токов через резисторы (используем для этой цели Закон Ома I = U / R):

Моделирование при помощи программы PSPICE подтвердит наши расчеты:

Источник