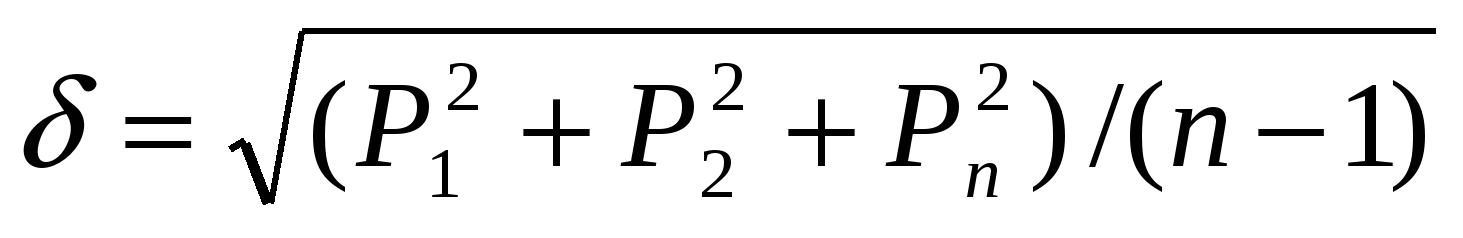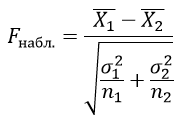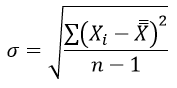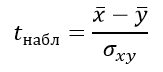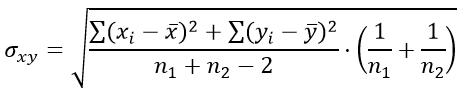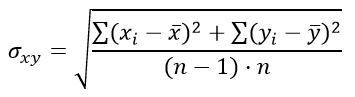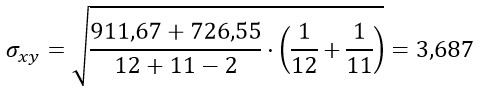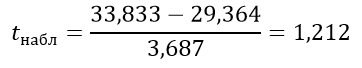Как посчитать погрешность по стьюденту

Как посчитать погрешность по стьюденту

Для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины несколько раз. Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины :

Так как оценочные значения результата измерений и ошибки Δx не являются точными, запись (3) результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью (3). Сам этот интервал называется доверительным интервалом.

Например, измеряя длину некоторого отрезка, окончательный результат мы записали в виде

Таким образом, задача заключается в том, чтобы, имея выборку (2), найти оценку результата измерений , его ошибку Δx и надежность P.

Эта задача может быть решена с помощью теории вероятностей и математической статистики.

В большинстве случаев случайные ошибки подчиняются нормальному закону распределения, установленного Гауссом. Нормальный закон распределения ошибок выражается формулой

где Δx – отклонение от величины истинного значения;

σ – истинная среднеквадратичная ошибка;

σ 2 – дисперсия, величина которой характеризует разброс случайных величин.

Поскольку кривая распределена симметрично относительно оси ординат, можно утверждать, что равные по величине, но противоположные по знаку ошибки равновероятны. А это дает возможность в качестве оценки результатов измерений взять среднее значение всех элементов выборки (2)

где – n число измерений.

Итак, если в одних и тех же условиях проделано n измерений, то наиболее вероятным значением измеряемой величины будет ее среднее значение (арифметическое). Величина стремится к истинному значению μ измеряемой величины при n → ∞.

Средней квадратичной ошибкой отдельного результата измерения называется величина

Она характеризует ошибку каждого отдельного измерения. При n → ∞ S стремится к постоянному пределу σ

С увеличением σ увеличивается разброс отсчетов, т.е. становится ниже точность измерений.

Среднеквадратичной ошибкой среднего арифметического называется величина

Это фундаментальный закон возрастания точности при росте числа измерений.

Ошибка характеризует точность, с которой получено среднее значение измеренной величины . Результат записывается в виде:

Эта методика расчета ошибок дает хорошие результаты (с надежностью 0.68) только в том случае, когда одна и та же величина измерялась не менее 30 – 50 раз.

В 1908 году Стьюдент показал, что статистических подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений n → ∞ переходит в распределение Гаусса, а при малом числе отличается от него.

Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом
Стьюдента t.

Опуская теоретические обоснования его введения, заметим, что

где Δx – абсолютная ошибка для данной доверительной вероятности;
– среднеквадратичная ошибка среднего арифметического.

Для этого удобнее воспользоваться таблицей 3, в которой интервалы заданы в долях величины σ, являющейся мерой точности данного опыта по отношению к случайным ошибкам.

Таблица 2

Таблица 3

При обработке результатов прямых измерений предлагается следующий порядок операций:

Рассмотрим на числовом примере применение приведенных выше формул.

Пример. Измерялся микрометром диаметр d стержня (систематическая ошибка измерения равна 0.005 мм ). Результаты измерений заносим во вторую графу таблицы, находим и в третью графу этой таблицы записываем разности , а в четвертую – их квадраты (таблица 4).

Таблица 4

Задавшись надежностью P = 0.95, по таблице коэффициентов Стьюдента для шести измерений найдем t = 2.57. Абсолютная ошибка найдется по формуле (10).

Сравним случайную и систематическую ошибки:

следовательно, δ = 0.005 мм можно отбросить.

Источник

Расчет погрешностей емкости с помощью коэффициента Стьюдента. Расчет погрешности измерения мощности и сопротивления

Отклонение результата измерения от истинного измеряемой величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности между результатом измерения Ах и истинным значением измеренной величины А:

Просмотр содержимого документа
«Расчет погрешностей емкости с помощью коэффициента Стьюдента. Расчет погрешности измерения мощности и сопротивления»

Лабораторная работа № 1.

Расчет погрешностей емкости с помощью коэффициента Стьюдента.

Расчет погрешности измерения мощности и сопротивления

Общеобразовательная – Умение решать задачи по теме погрешности.

Воспитательная – Проверить сформированность качеств знаний.

Отклонение результата измерения от истинного измеряемой величины называют погрешностью измерения.

Абсолютная погрешность измерения ΔА равна разности между результатом измерения Ах и истинным значением измеренной величины А:

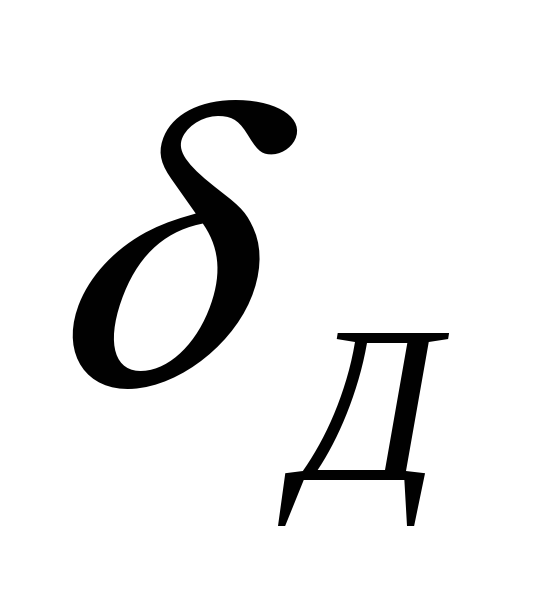
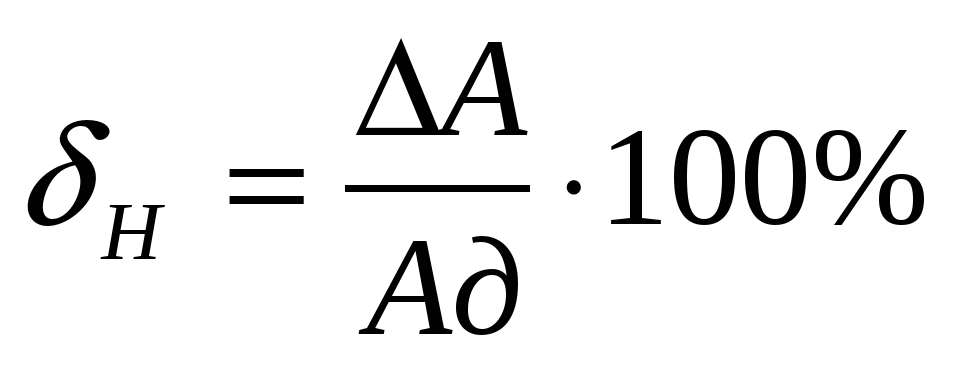
Действительная относительная погрешность представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины, выраженное в процентах:

(2)

Номинальная относительная погрешность, равная отношению абсолютной погрешности к измеренному значению исследуемой величины,

(3)

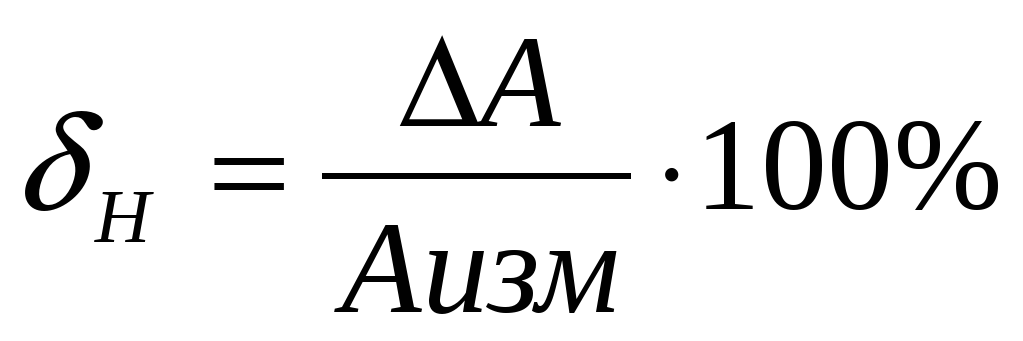
Приведенная относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к максимальному значению измерительного прибора

(4)

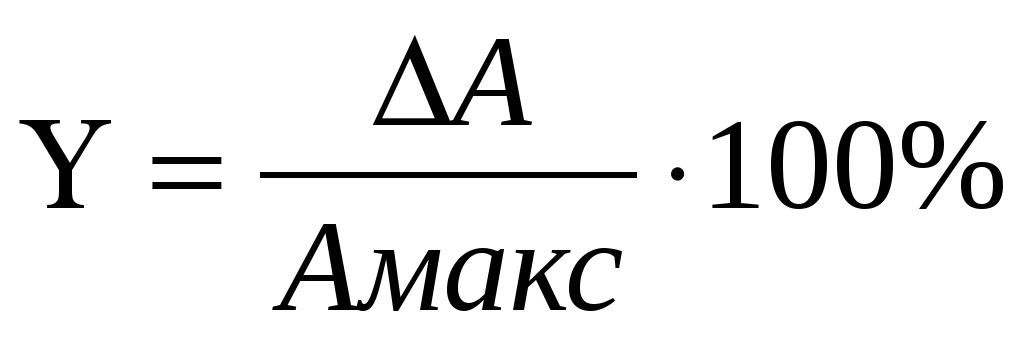
Для приборов с двухсторонней шкалой А_макс определяется как сумма абсолютных величин положительного и отрицательного пределов измерения.

Если шкала начинается не с нуля, а с какого-то минимального значения, то А_макс равно разности между конечным и начальным значениями шкалы.

Случайными называются погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности нельзя исключить опытным путем, т. к. они возникают случайно. Для того, чтобы исключить случайные погрешности производят неоднократные измерения и определяют среднее арифметическое из полученных значений, определяемое как

,

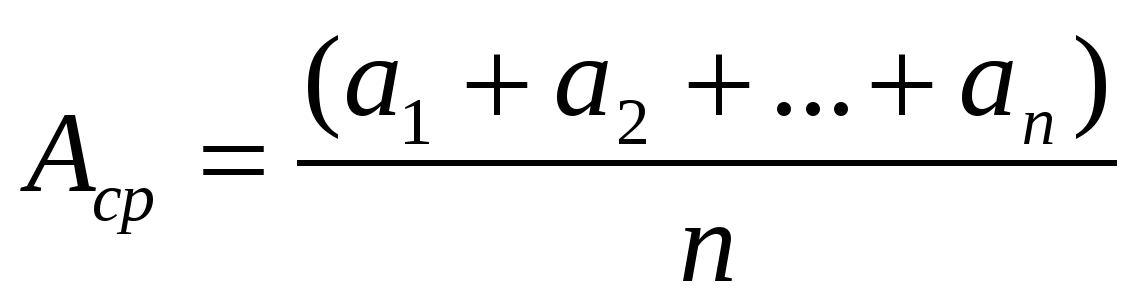
где а₁, а₂, …, а_n – результаты отдельных измерений;

n – число измерений.

Для оценки точности результата измерений необходимо знать закон распределения случайных погрешностей, таким законом является нормальный закон Гаусса. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдения Р:

Этот способ определения доверительных интервалов справедлив толко для больших количеств измерений (20-30). Для небольшого количества измерений для определения доверительного интервала нужно пользоваться коэффициентами Стьюдента t_n, которые зависят от задаваемой доверительной вероятности Р и количества измерений n.

Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат измерения можно записать так:

А = Аср t_n

Задача 1. Для уменьшения влияния случайных погрешностей на результат измерения, емкость конденсатора С измерялась многократно в одинаковых условиях (таблица 1). Считая, что случайные погрешности имеют нормальный закон распределения, определить на основании заданного количества измерения (табл. 1, табл. 2):

Действительное значение измеряемой емкости;

Среднюю квадратическую и максимальную погрешности однократного измерения;

Доверительный интервал для результата измерения при доверительной вероятности Р_д (табл.3).

Имеется ли систематическая составляющая в погрешности измерения емкости и с какой доверительной вероятностью ее можно оценить, если принять в качестве действительного значения емкости значения С_ср (таб.1, таб.2).

Источник

Критерий Стьюдента

Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины.

Критерий Стьюдента определяется по формуле:

$\bar$ – выборочные средние значения первой выборки;

$\bar$ – выборочные средние значения второй выборки;

n₁ – объем первой выборки;

n₂ – объем второй выборки;

σ₁ и σ₂ – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:

Число степеней свободы определяется по формуле:

F_кр(α, k) определяется по таблице

Формула критерия Стьюдента для несвязанных независимых выборок:

Формула для определения стандартной ошибки разности средних арифметических σ_xy:

Число степеней свободы определяется выражением:

При n₁=n₂ число степеней свободы находится по формуле:

k=2n-2

а стандартная ошибка разности средних арифметических σ_xy задаётся выражением:

Пример

В первой выборки продажа товара со скидкой, а во второй без скидки.

По критерию Стьюдента определить зависит ли спрос на товар от скидок на него при p=0.99?

Решение

В соответствии с таблицей n₁=12, n₂=11

Вычислим дисперсии D(X), D(Y)

Подставим значения в формулу стандартной ошибки разности средних арифметических σ_xy:

Вычисляем критерий Стьюдента:

Число степеней свободы равно:

k=12+11–2=21

По таблице Стьюдента находим критическое значение:

t_крит=2,8310

Отсюда t_крит> t_набл, следовательно, зависит.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.4 / 5. Количество оценок: 13

Источник