Как посчитать объем в сантиметрах
Как посчитать объем в сантиметрах


Ваша заявка успешно отправлена, наши менеджеры свяжутся с Вами в ближайшее время.
Ваш вопрос успешно отправлен, мы постараемся ответить на него как можно скорее.
Мы свяжемся с вами в ближайшее время для подтверждения доставки. Номер накладной и прочая информация будет отправлена на указанные E-mail адреса отправителя и получателя.
Также через личный кабинет вы можете в режиме онлайн видеть состояние ваших отправлений и получений
Мы свяжемся с вами в ближайшее время для подтверждения доставки. Номер накладной и прочая информация будет отправлена на указанные E-mail адреса отправителя и получателя.
Если вы хотите чтобы данные о состояние ваших отправлений и получений были сохранены, зарегистрируйтесь или авторизуйтесь в личном кабинете.
Данные из калькулятора сохранены в черновике.
Вы можете продолжить оформление заявки на доставку в личном кабинете.
Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
Как рассчитать объём ёмкости, воды или другой жидкости … несколько онлайн калькуляторов для расчёта объёма, формулы, а также конвертер единиц объёма.
Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …
Формула расчёта объёма прямоугольной ёмкости
V = X * Y * Z, где V — объём, а X, Y, и Z это длины сторон ёмкости (длина, ширина, высота).
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать реальную заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
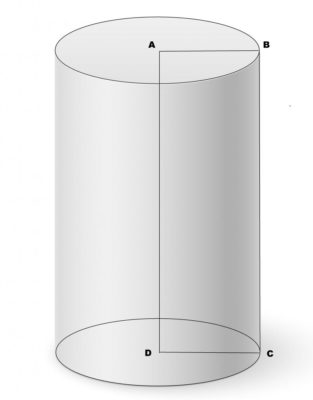
Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Формулы расчёта объёма цилиндра:
Объём воды в цилиндре и других ёмкостях, имеющих цилиндрическую форму, рассчитывается таким образом.
Затем вычисляем объём — V = S * L
Где, L — длина (высота) цилиндра (трубы, бочки, бассейна).
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Единицы измерения объёма
Вначале кратко ознакомимся с единицами измерения объёма как таковыми.
Официальной единицей измерения объема в системе СИ является м 3 — метр кубической. Объём так же может быть выражен и в других единицах. Наиболее популярными из них являются — дм 3 — кубические дециметры, см 3 — кубические сантиметры, литры …
Отметим, что такая популярная единица измерения объёма жидкостей как литр не входит в Международную систему измерений (СИ). Тем не менее, поскольку литр является весьма популярной мерой жидкостей, он считается официальной внесистемной единицей.
Один литр — это объём куба стороны которого равны 10 см. Полезно также знать, что 1 литр воды вести приблизительно 1 кг при температуре + 4 °C
Соотношение единиц объёма
1 м3 = 1000 дм 3 = 1 000 000 см 3 = 1 000 000 000 мм 3 = 1000 литров
1 литр = 0,001 м 3 = 1 дм 3 = 1 000 см 3 = 1 000 000 мм 3
Конвертер единиц объёма
Конвертация кубических метров ( м 3 ) в кубические сантиметры ( см 3 ) и литры
Конвертация литров в метры кубические ( м 3 ) и кубические сантиметры ( см 3 )
Конвертация кубических сантиметров ( см 3 ) в кубические метры ( м 3 ) и литры
Заключение
Практически каждый человек рано или поздно сталкивается с необходимостью рассчитать объём того или другого объекта. Для удобства и экономии времени предлагаем Вам воспользоваться нашими онлайн калькуляторами.
Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
1 комментарий к “Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …”
Быстро и удобно если много объёмов
Оставьте комментарий Отменить ответ
Поделись с друзьями 🙂
Рубрики сайта
Публикации
Публикации
Поиск по сайту
Все материалы сайта защищены Законом «Об авторском праве и смежных правах». Сайт – vodamama.com является общедоступным и работает в рамках и в соответствии с действующим законодательством Украины.
Администрация ресурса может не разделять мнение автора. При подготовке материалов информация берётся из общедоступных источников и специальной проверки на достоверность не проходит.
Администрация сайта радикально негативно относится к нарушениям авторских или каких либо других имущественных прав. Поэтому, если Вы вдруг обнаружили, что на страницах нашего сайта нарушены, какие либо авторские или имущественные права, просим вас незамедлительно, воспользовавшись формой обратной связи, сообщить нам про это. После получения подтверждения нарушения мы незамедлительно устраним его.
Как найти объём геометрических фигур
Изучение объемных фигур начинается со школы. В это время происходит знакомство с цилиндром, параллелепипедом, шаром, конусом и другими геометрическими телами. Одна из главных задача, которая сопровождает учеников, это вычисление объема фигур. Оперируя формулами, удается произвести расчет и получить ответ в метрах кубических (м 3 ).
Чтобы вычислить объем, применяйте следующее правило – длину, ширину и высоту нужно перемножить между собой. Объем для каждой фигуры рассчитывается по специальной формуле, о которых, мы расскажем ниже.
Содержание:
Как найти объем трехмерных объектов
Начнем с расчета для прямоугольных и квадратных фигур. Придерживайтесь инструкции и постарайтесь рассчитать самостоятельно, чтобы закрепить знания. Числа, указанные в описании, берутся в качестве примера. Вы можете производить другие расчеты.
Полученное число необходимо перевести в кубические метры. Для этого конечный результат делим на 1.000.000. Пример будет выглядеть следующим образом – 4256 м 3 /1000000 = 0,004256 м 3
Как найти объем для фигур цилиндрической формы
Цилиндр – это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Одним из видов цилиндра является призма.
Чтобы произвести вычисления нужно найти диаметр тела (ширина) одного круглого основания и полученное число поделить на 2. Допустим, диаметр основания равен 30 см.
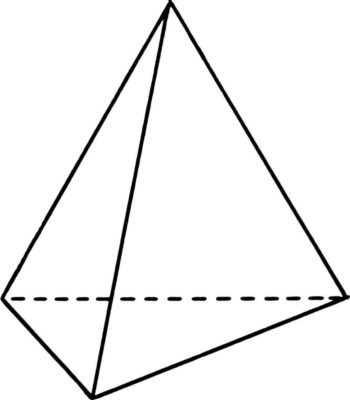
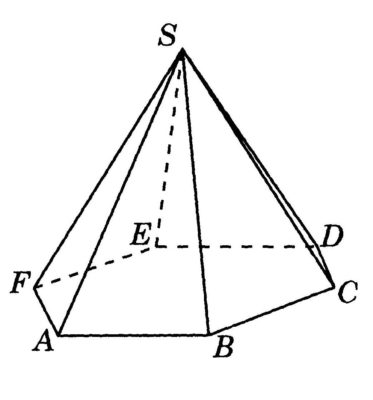
Как рассчитать объем треугольной пирамиды
Пирамида – это многогранник, где есть одна грань основания и боковые грани. Пирамиды бывают треугольные, четырехугольные и другие. Также есть правильная и усеченная пирамида. Объем для каждой фигуры рассчитывается по разным формулам.
Расчёт четырехгранной пирамиды производится тем же принципом. Потренируйтесь, используя разные задачи. Чтобы все замеры происходили правильно, не забудьте обзавестись хорошей линейкой, также на помощь придёт калькулятор, который поможет перемножать числа между собой.
В интернете представлено много онлайн-калькулятор, они дают подсказку и позволяют без лишних трудностей рассчитать объём куба, цилиндра и других фигур. Перед началом пользования таких подсказок, необходимо обладать базовыми знаниями, чтобы быстрее разобраться в полученном результате.
Как посчитать объем куба
Параллелепипед складывается из шести граней, которые являются параллелограммом. Все противоположные грани попарно равны и параллельны. Фигура получилась 4 диагонали, и все они пересекаются в одной точке, разделяют эту точку пополам. Параллелепипед, грани которого являются квадратами, будет называться кубом.
Как найти объем прямоугольного параллелепипеда
Прямоугольным параллелепипедом называется фигура, у которой все шесть граней прямоугольники. Для вычисления работает следующая формула:
Где H ‒ высота, S ‒ площадь основания, abc – ребра. Чтобы произвести расчеты и найти объём, необходимо узнать произведение площади основания на высоту. Например: 1 см * 2 см * 3 см = 6 см 3
Советы по измерению:
Убедитесь, что перед вами параллелепипед, а не куб, так как в случае с кубом расчетная формула будет проще.
Как найти объем цилиндра
Цилиндр считать круглой фигурой, т.к. в его основании лежит круг. Чтобы произвести вычисления, необходимо узнать произведение площади основания на высоту. Для этого используется следующая формула:
Где r ‒ радиус цилиндра, h – высота цилиндра. Чисто π – является константой и равно 3,14. Оно всегда одинаковое и не требует никаких измерений. Рассмотрим на примере:
3,14 * 2 см 2 * 5 см = 62.831853071796 = 63см 3
Если вы не можете вычислить радиус, измерьте диаметр с помощью формулы преобразования.
Как найти объем пирамиды
фото 6 — посчитать объём
Чтобы произвести расчет объема, нам нужно найти произведение площади основания на высоту. Для вычисления используется следующая формула:
Где S (A*B*C*D*E) – площадь основания пирамиды, а h ‒ высота пирамиды. Рассмотрим на примере:
V = 3 * 2 = 2 см 3 ‒ это и будет являться объемом искомой геометрической фигуры.
Не забывайте, что пирамиды бывают усеченные, правильные, трех- и четырехугольные. Для каждого тела действуют свои расчеты, но важно начинать с основного и не упускать базовые знания, в дальнейшем все примеры будут базироваться именно на них.
Если какая-то формула осталась непонятной, лучше вернуться к этому и поупражняться ещё раз, доведя знание до автоматизма. Так решение задач не будет вызывать сложности. Постоянная практика ‒ это основа успешного результата.
Как рассчитать объем коробки
Картонная коробка служит популярной тарой для упаковки товаров и различных предметов с целью их транспортировки или хранения. На рынке гофротары представлены как потребительские, индивидуальные упаковки, так и транспортная тара. Такой вид упаковки является эргономичным и экологически чистым.
Производство картонной упаковки на высокотехнологичном оборудовании дает возможность изготавливать тару различных размеров и дизайна. К примеру, известным поставщиком картонно-бумажных коробок является компания «Тара для товара», которая успешно реализует свою продукцию по всей России.
Чтобы правильно определить вместимость и необходимые размеры тары для груза, следует рассчитать объем коробки.
Как посчитать объем коробки в М 3
Во время фасовки и транспортировки товаров, предприниматели задаются вопросом, как это правильно сделать, чтобы сэкономить время и финансы. Расчет объема тары является важным моментом в доставке. Изучив все нюансы, Вы сможете подобрать необходимую по размерам коробку.
Как рассчитать объем короба? Чтобы груз без проблем поместился в короб, его объем необходимо высчитывать, пользуясь внутренними размерами.
Воспользуйтесь онлайн калькулятором для вычисления объема коробки в форме куба или параллелепипеда. Он поможет ускорить процесс расчетов.
Груз, который необходимо поместить в тару, может быть простой или сложной конфигурации. Габариты короба должны быть на 8-10 мм больше самых выступающих точек груза. Это необходимо, чтобы предмет без затруднений поместился в тару.
Наружные размеры используют при подсчетах объемов коробок, чтобы грамотно заполнить пространство в кузове транспорта для перевозки. Также они нужны для вычисления площади и объема склада, необходимого для их хранения.
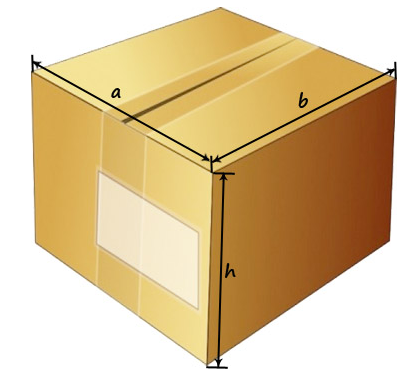
Во-первых, измерим длину (а) и ширину (b) коробки. Для этого будем пользоваться рулеткой или линейкой. Результат можно записать и перевести в метры. Будем пользоваться международной системой измерений SI. Согласно ей, объем емкости рассчитывается в кубических метрах (м 3 ). Для тары, стороны которой меньше метра, удобней производить замеры в сантиметрах или миллиметрах. Необходимо учитывать, что габариты груза и коробки должны быть в одних и тех же единицах измерения. Для квадратных коробок длина равняется ширине.
Затем произведем замеры высоты (h) имеющейся тары ─ расстояние от нижнего клапана коробки до верхнего.
Учитывая, что 1 м=1000 м, переведем эти значения в метры, а затем подставим в формулу.
Формулы
Используя формулу подсчета объема коробки получим:
V=a*b*h =0,3*0,25*0,15=0,0112 м 3.
Такой метод можно использовать при расчете объема параллелепипеда, то есть для прямоугольных и квадратных коробок.
Подсчет объема коробки в литрах
При транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах. Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м 3 ;
зная равенство: 1 м 3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л.
Площадь основания коробки
Приведенные выше формулы применяются для подсчета объема тары в форме параллелепипеда. При не стандартных формах площадь объем коробки считается по формуле:
Формула площади S основания коробки (контейнера) необходимо менять в зависимости от формы тары.
S=a*b; S=a 2 =а*а берем в случае, когда у нас картонное изделие прямоугольной или квадратной формы.
Некоторые товары, требующие транспортировки, имеют особенные параметры.
В таких случаях требуется упаковать товар в тару из картона сложной конфигурации, которая имеет нестандартную форму и эксклюзивный дизайн, способный выделить ее содержимое среди похожей продукции. Для этого и нужно знать, как посчитать площадь коробки другой конфигурации. Будем использовать формулы для нахождения площади многоугольника: треугольника, шестиугольника и восьмиугольника.
Этой формулой можно воспользоваться для расчета площади основания Вашей тары, если она имеет форму треугольника. Умножив полученное значение на высоту, получите значение объема короба в форме призмы.
В других случаях, смотрите, какая фигура находится в основании конкретной коробки, берите формулу для нахождения ее площади, а затем умножайте полученный результат на высоту.
Работаем для Вас с 2009 года! Собственное производство, товарный запас на складах и опытный персонал! Тысячи довольных клиентов по всей России ежедневно экономят свои время и деньги с помощью нашего сервиса!
Объемы фигур. Объем куба.
У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.
Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна
где s – длина одного (любого) ребра куба.

Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.
Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.
Метод 1 из 3: Возведение в куб ребра куба
вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.
и, таким образом, вы вычислите объем куба.
Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на
ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,
другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и
равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.
В нашем примере объем куба равен:
характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические
В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических
Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих
Метод 2 из 3: Вычисление объема по площади поверхности
можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите
ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем
возведите длину ребра куба в третью степень и вычислите объем куба.
где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так
как у куба 6 равных граней).
одной грани и получите длину ребра куба.
В нашем примере, √8,33 = 2,89 см.
Метод 3 из 3: Вычисление объема по диагонали
если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив
Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба
которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен
сумме квадратов катетов (в нашем случае ребер), то есть:
дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.
Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае
диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –
это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть
Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.