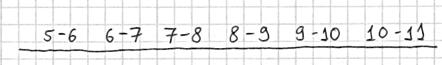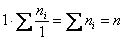Как посчитать интервал в статистике

Определение числа групп и интервалов группировки

Тема. 3. Статистическая сводка и группировка

Понятие сводки и группировки

Определение числа групп и интервалов группировки

Статистический ряд распределения

4. Статистическая таблица

Понятие сводки и группировки

На основе информации собранной в ходе статистического наблюдения, как правило, нельзя непосредственно выявить и охарактеризовать закономерности социально-экономических явлений. Это связано с тем, что наблюдение дает сведения по каждой единице исследуемого объекта. Поэтому цель следующего этапа статистического исследования состоит в систематизации первичных данных и получение на этой основе сводной характеристики всего объекта при помощи обобщающих статистических показателей.

Сводка представляет комплекс последовательных действий по обобщению конкретных единичных данных, образующих совокупность, в целях выявления типических черт и закономерностей, присущих изучаемому явлению в целом.

Задача сводки охарактеризовать исследуемый объект с помощью системы статистических показателей, выявить и измерить таким путем его существенные черты и особенности.

Основой сводки является статистическая группировка, представляющая собой разделение множества единиц изучаемой совокупности на группы по определенным существенным для них признакам.

С помощью метода группировок решаются следующие задачи:

– выделение социально-экономических типов явлений;

– изучение структуры явления и структурных сдвигов, происходящих в нем;

– выявление связи и зависимости между признаками изучаемых явлений.

По основным показательным задачам группировки подразделяются на типологические, структурные и аналитические группировки.

По степени сложности различают простые и комбинированные (комбинационные) группировки. Все группировки, производимые по одному признаку, называются простыми, по двум и более признакам – сложными или комбинированными.

При статистическом исследовании иногда приходится производить вторичную группировку, т. е. перегруппировывать статистический материал, уже сведенный в группы. Вторичная группировка может производиться путем сведения в новые группы по тому же признаку, по которому произведена первичная группировка статистических данных. В этом случае интервалы первичной группировки либо укрупняются, либо, наоборот, расчленяются.

Определение числа групп и интервалов группировки

Прежде чем приступить к группировке статистических данных, необходимо определить основание группировки, т.е. выделить группировочный признак. Группировочный признак – это признак, по которому проводится разбивка единиц совокупности на группы.

Образование групп и интервалов группировки, при правильном выбранном группировочном признаке зависит от цели исследования, от признака, положенного в основание группировки, и характера вариации. Количество образуемых групп в некоторых случаях определяется признаком, положенным в основание группировки. Так, выбор в качестве группировочных некоторых атрибутивных признаков сам по себе предопределяет решение вопроса о числе групп. Например, группировка населения по полу приводит к образованию всего лишь двух групп. Если же в основание группировки положен количественный признак, то возникает вопрос не только о числе групп, но и об интервалах – их характере (равные, неравные и др.) и величине.

Число групп можно ориентировочно определить по формуле Стерджесса:

, (1)

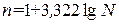
где N – число единиц в совокупности.

После определения числа групп следует определить интервалы группировки. Интервал – это значения признак, лежащие в определённых границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Нижней границей интервал, называется наименьшее значение признака в нем, верхней – наибольшее. Закрытыми называются интервалы, у которых обозначены обе границы. Открытые – интервалы, у которых указана только одна граница: верхняя у первого, и нижняя у последнего. Величина интервала – это разность между верхней и нижней границей интервала.

Интервалы бывают равные и неравные. Величину интервала при группировке с постоянным интервалом определяют по формуле:

, (2)

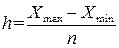
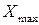
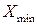
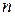
где , – наибольшее и наименьшее значения признака в изучаемой совокупности;

– число выделяемых групп.

При построение группировок возникает вопрос, в какую группу включать единицы объекта, значения признака у которых совпадает с границами интервалов. В этом случае применяют следующие принципы: нижняя граница формируется по принципу включительно, а верхняя – исключительно или наоборот, а так же используют открытые интервалы.

Пример. Требуется произвести группировку с равным интервалами предприятия по стоимости основных фондов, при этом максимальное значение признака 2040 тыс. ден. ед., минимальное – 290 тыс. ден. ед. Совокупность включает 80 предприятий.

1. Основные производственные фонды – группировочный признак.

2. Число групп определяем используя формулу (1):

.

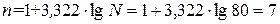
3. Величину интервала определяем по формуле (2):

тыс. ден. ед.

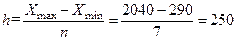
4. Строим интервалы групп:

Таблица 1 – Варианты построения групп

Особенность первого варианта построения групп является то, что у всех групп имеются закрытые интервалы. Во втором варианте первая и последняя группы – это группы с открытыми интервалами.

Предприятия, например, со стоимость фондов 790 тыс. ден. ед. будет включено в третью группу, 1540 – в шестую и т.д.

Источник

3. Интервальный вариационный ряд.
Гистограмма относительных частот

На предыдущем уроке по математической статистике (Занятие 1) мы разобрали дискретный вариационный ряд (Занятие 2), и сейчас на очереди интервальный. Его понятие, графическое представление (гистограмма и эмпирическая функция распределения), а также рациональные методы вычислений, как ручные, так и программные. В том числе будут рассмотрены задачи с достаточно большим количеством (100-200) вариант – что делать в таких случаях, как обработать большой массив данных.

Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений. Зачастую ИВР появляется в результате измерения непрерывной характеристики изучаемых объектов. Типично – это время, масса, размеры и другие физические характеристики. Подходящие примеры встретились в первой же статье по матстату, вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.

Для изучения интервального вариационного ряда затруднительно либо невозможно применить тот же подход, что и для дискретного ряда. Это связано с тем, что ВСЕ варианты многих ИВР различны. И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, ибо полученные значения всё равно отличаются хоть какими-то микрограммами.

Поэтому для исследования ИВР используется другой подход, а именно, определяется интервал, в пределах которого варьируются значения, затем данный интервал делится на частичные интервалы, и по каждому интервалу подсчитываются частоты – количество вариант, которые в него попали.

Разберём всю кухню на конкретной задаче, и чтобы как-то разнообразить физику, я приведу пример с экономическим содержанием, кои десятками предлагают студентам экономических отделений. Деньги, строго говоря, дискретны, но если надо, непрерывны :), и по причине слишком большого разброса цен, для них целесообразно строить интервальный ряд:

По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в некоторых денежных единицах):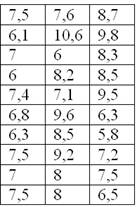

Требуется составить вариационный ряд распределения, построить гистограмму частот, гистограмму и полигон относительных частот + бонус – эмпирическую функцию распределения.

Такое обывательское исследование проводит каждый из нас, начиная с анализа цены на пакет молока вот это дожил в нескольких магазинах, и заканчивая ценами на недвижимость по гораздо бОльшей выборке. Что называется, не какие-то там унылые сантиметры.

Поэтому представьте свой любимый товар / услугу и наслаждайтесь решением🙂

Очевидно, что перед нами выборочная совокупность объемом 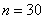наблюдений (таблица 10*3), и вопрос номер один: какой ряд составлять – дискретный или интервальный? Смотрим на таблицу: среди предложенных цен есть одинаковые, но их разброс довольно велик, и поэтому здесь целесообразно провести интервальное разбиение. К тому же цены могут быть округлёнными.

Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.

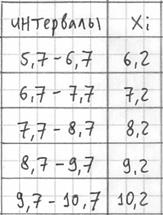
Тактика действий похожа на исследование дискретного вариационного ряда. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:

Теперь начинаем вычёркивать числа из исходного списка и записывать их в соответствующие колонки нашей импровизированной таблицы: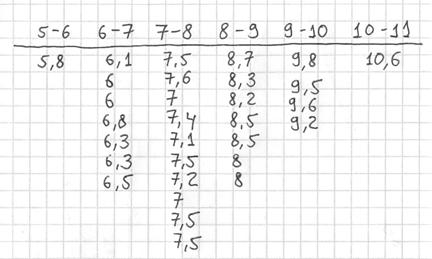

После этого находим самое маленькое число в левой колонке и самое большое значение – в правой. Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
ден. ед. – хорошим тоном считается указывать размерность.

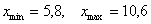
Вычислим размах вариации:
ден. ед. – длина общего интервала, в пределах которого варьируется цена.

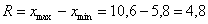
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса:

, где – десятичный логарифм* от объёма выборки и – оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.

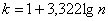
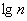
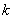
* есть на любом более или менее приличном калькуляторе

В нашем случае получаем:
интервалов.

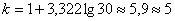
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов нужно проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.

Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
– длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.

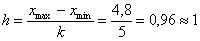
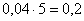
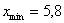
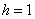
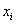
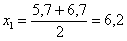
И коль скоро мы прибавили 0,04, то по 5 частичным интервалам у нас получается «перебор»: . Посему от самой малой варианты отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины (например, ) – они требуются почти во всех тематических задачах:

– убеждаемся в том, что самая большая варианта 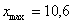вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.

Далее подсчитываем частоты по каждому интервалу. Для этого в черновой «таблице» обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем: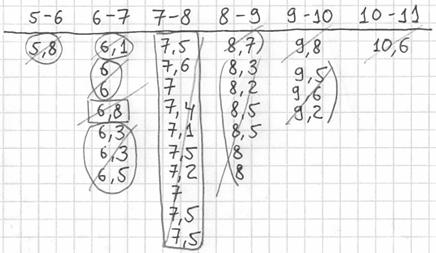

Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее.

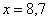
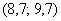
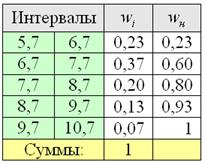
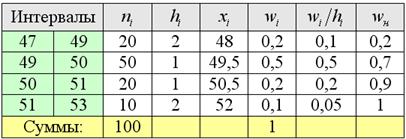
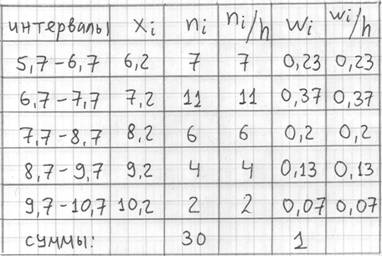
Правило: если варианта попадает на «стык» интервалов, то её следует относить в правый интервал. У нас такая варианта встретилась одна: – и её нужно причислить к интервалу .

В результате получаем интервальный вариационный ряд:

при этом обязательно убеждаемся в том, что ничего не потеряно: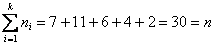
, ОК.

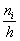
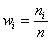
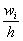
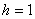
Изобразим ряд графически. Для этого по каждому интервалу нужно найти (не пугаемся): плотность частот , относительные частоты (округляем их до 2 знаков после запятой), а также плотность относительных частот . Поскольку длина частичного интервала , то вычисления заметно упрощаются:

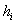
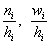
В том случае, если интервалы имеют разные длины , то при нахождении плотностей каждую частоту нужно делить на длину своего интервала: . Но у нас популярная равноинтервальная группировка, да не абы какая, а с единичным частичным интервалом. Возьмите на заметку всю выгоду такого интервала.

Дело за чертежами. Один за другим.

Гистограмма частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям частот: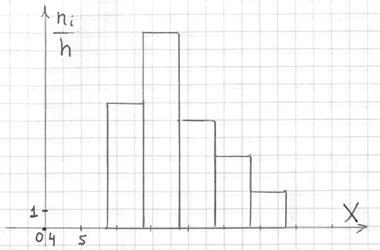

При этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх.

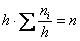
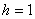
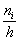
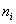
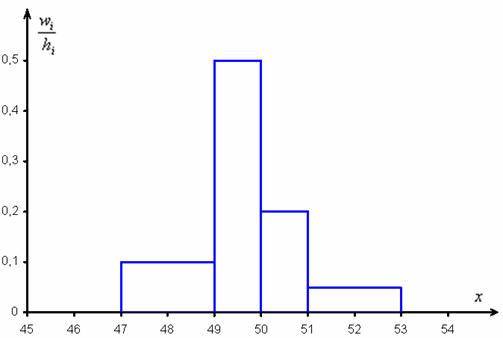
Площадь гистограммы частот в точности равна объёму совокупности: . В нашем случае и плотности совпали с самими частотами , таким образом:

Гистограмма относительных частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим плотностям относительных частот: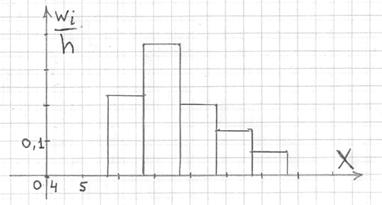

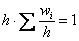
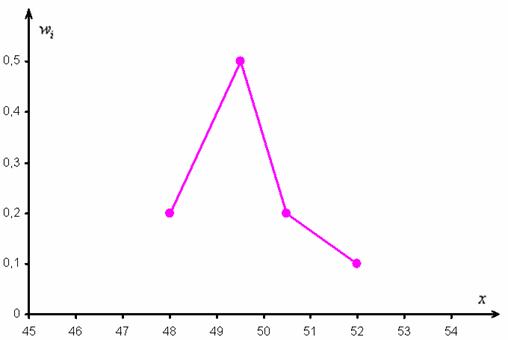
Площадь такой гистограммы равна единице: , и это статистический аналог функции плотности распределения непрерывной случайной величины. Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. Но это при условии, что выборка представительна.

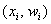
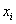
И для ИВР чаще всего строят гистограмму именно относительных частот. А вместе с ней нередко и полигон таковых частот. Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки , где – середины интервалов:

По сути, здесь мы приблизили интервальный ряд дискретным, выбрав в качестве вариант 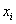середины интервалов. Это важнейший принцип и метод, который неоднократно встретится нам в последующих задачах.

Автоматизируем решение в Экселе:

Как составить ИВР и представить его графически? (Ютуб)

(видео с неточностями, скоро исправлю и перезалью)

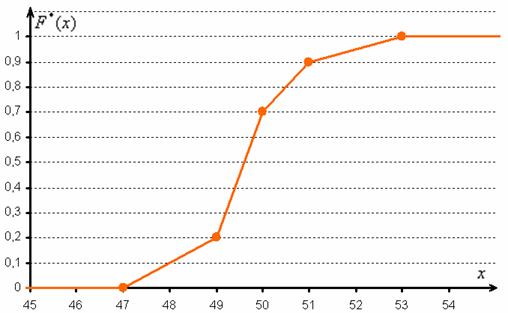
И бонус – эмпирическая функция распределения. Она определяется точно так же, как в дискретном случае:

, где – количество вариант СТРОГО МЕНЬШИХ, чем «икс», который «пробегает» все значения от «минус» до «плюс» бесконечности.

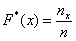
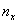
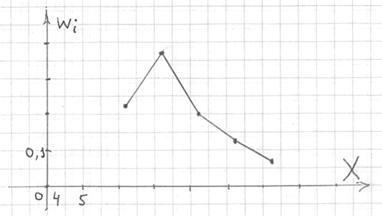
Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:

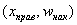
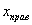
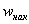
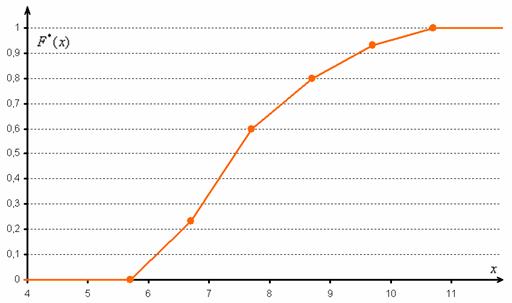
И строим кусочно-ломаную линию, с промежуточными точками , где – правые концы интервалов, а – относительная частота, которая успела накопиться на всех «пройденных» интервалах:

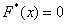
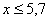
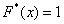
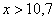
При этом если и если .

Напоминаю, что данная функция не убывает, принимает значения из промежутка 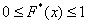и, кроме того, для ИВР она ещё и непрерывна.

Эмпирическая функция распределения является аналогом функции распределения НСВ и приближает теоретическую функцию 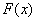, которую теоретически, а иногда и практически можно построить по всей генеральной совокупности.

Помимо перечисленных графиков, вариационные ряды также можно представить с помощью кумуляты и огивы частот либо относительных частот, но в классическом учебном курсе эта дичь редкая, и поэтому о ней буквально пару абзацев:

Кумулята – это ломаная, соединяющая точки:

* либо – для дискретного вариационного ряда;
либо – для интервального вариационного ряда.

* – накопленные «обычные» частоты

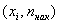
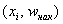
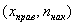
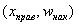
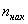
В последнем случае кумулята относительных частот 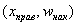представляет собой «главный кусок» недавно построенной эмпирической функции распределения.

Огива – это обратная функция по отношению к кумуляте – здесь варианты откладываются по оси ординат, а накопленные частоты либо относительные частоты – по оси абсцисс.

С построением данных линий, думаю, проблем быть не должно, чего не скажешь о другой проблеме. Хорошо, если в вашей задаче всего лишь 20-30-50 вариант, но что делать, если их 100-200 и больше? В моей практике встречались десятки таких задач, и ручной подсчёт здесь уже не торт. Считаю нужным снять небольшое видео:

Как быстро составить ИВР при большом объёме выборки? (Ютуб)

Ну, теперь вы монстры 8-го уровня 🙂

Но не всё так сурово. В большинстве задач вам предложат готовый вариационный ряд, и на счёт молока, то, конечно, была шутка:

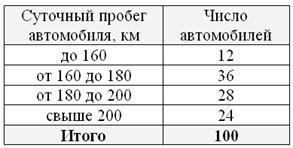
Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:

Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения

Проверяем свои навыки работы в Экселе! (исходные числа и краткая инструкция прилагается) И на всякий случай краткое решение для сверки в конце урока. Должен признаться, я немного усложнил это задание, сделав интервалы разной длины – для лучшего понимания материала.

Что ещё важного по теме? Время от времени встречаются ИВР с открытыми крайними интервалами, например:

В таких случаях, что убийственно логично, интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину частичного интервала: 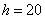км. И для дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км. Тоже логично. Но уже не убийственно:) Если внутренние интервалы имеют разные длины, то для крайних интервалов можно взять среднюю арифметическую известных длин.

Ну вот, пожалуй, и вся практически важная информация по ИВР.

На очереди числовые характеристики вариационных рядов и начнём мы с их центральных характеристик, а именно – Моды, медианы и средней.

Пример 7. Решение: в данной задаче интервалы имеют разные длины 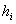, заполним расчётную таблицу:

Построим гистограмму относительных частот:

Построим полигон относительных частот:

Построим эмпирическую функцию распределения:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник