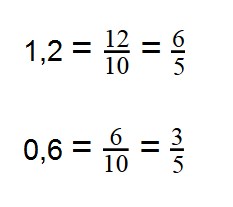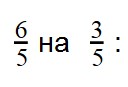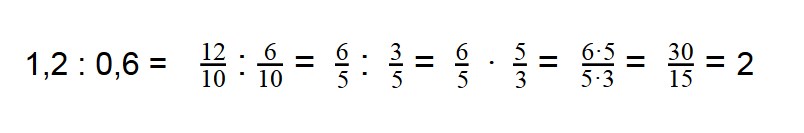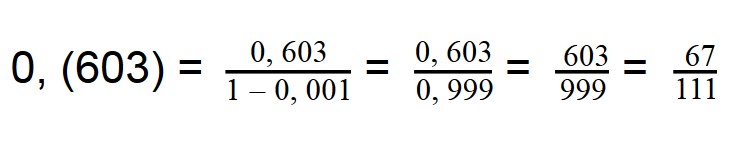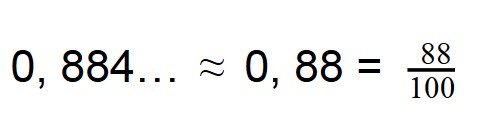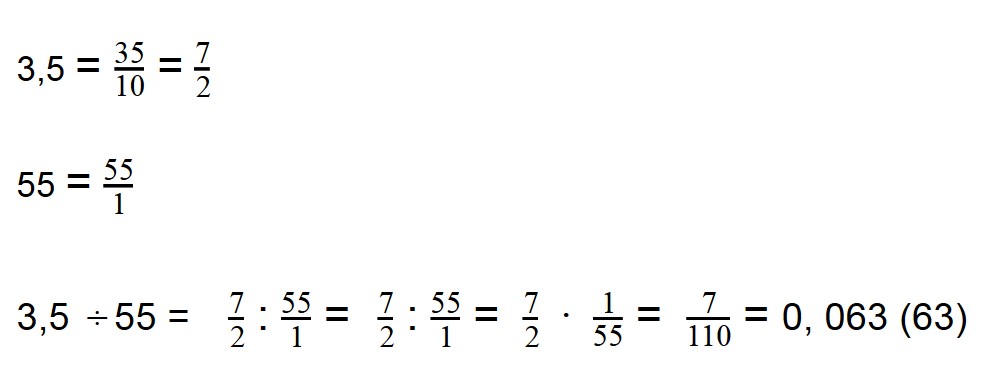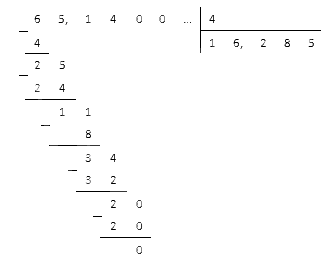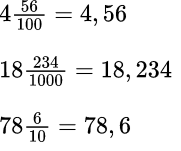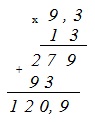Как посчитать десятичные дроби столбиком
Деление десятичных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основы деления десятичных дробей
Десятичные дроби — это дроби, у которых в знаменателе стоят числа, кратные 10. То есть 10, 100, 1000 и так далее.
Как делить десятичные дроби друг на друга — процесс представляет собой деление обыкновенных дробей. То есть для выполнения действий деления мы переписываем десятичную дробь в стандартный вид.
Рассмотрим пример: разделите 1,2 на 0,6
Как решаем
Запишем десятичные дроби в виде обыкновенных. У нас получится:
Таким образом, нам надо разделить
Ответ: 1,2÷0,6 = 2
Если для деления нам попадается периодические и непериодические дроби, то действуем следующим образом.
Периодические переводим в обыкновенную:
Если же встречается непериодическая десятичная дробь, то мы ее округляем до сотых и дальше делим, как обычно:
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Как разделить целое число на десятичную дробь и наоборот
Здесь всё просто: приводим десятичную дробь к стандартному виду и натуральное число тоже представляем в виде дроби — само число нужно поделить на единицу.
Пример: 3,5 поделить на 55
Как решаем
Ответ: 3,5÷55 = 0,063 (63)
Как разделить десятичную дробь на натуральное число столбиком
Делить столбиком можно не только натуральные числа, но и дроби. Алгоритм мы подробно опишем здесь. Итак, как делить десятичные дроби на натуральные числа в столбик:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Выполнить деление по стандартной схеме. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться — получится периодическая дробь.
Пример: Разделить столбиком 49,14÷3
Как решаем
1. Делим столбиком, предварительно дописав два нуля к десятичной дроби.
2. После того, как мы поделили целую часть дроби и получили 16, отделяем ответ запятой (16) и продолжаем деление уже для дробной части
В конце у нас нулевой остаток, значит деление завершено.
Ответ: 49,14÷3 = 16,38
Как разделить столбиком одну десятичную дробь на другую
Все просто: умножаем делимое и делитель на 10, 100 и так далее — так, чтобы делитель превратился в натуральное число. А потом решаем также, как в примере выше:
1. Переносим запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, дописываем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Пример: поделить столбиком 63,42 на 2,1
Как решаем
Переносим запятую на один знак вправо, чтобы делитель (2,1) стало натуральным числом. Запятую переносим в обоих числах — у нас получается 634,2÷21.
Затем производим деление
Ответ: 63,42÷2,1 = 30,2
Как разделить десятичные дроби на 1000, 100, 10 и другие
Как вы уже заметили, есть основное правило деления десятичных дробей: по нему деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и другие.
Чтобы выполнить действие, нужно просто перенести запятую влево на нужное количество цифр (равное нулям). Если значений в числе не хватит для переноса — дописываем нужное количество нулей:
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и другие
Правило из предыдущего пункта поможет нам без труда разделить дроби на указанные значения. Переводим эти числа в стандартные дроби и затем при делении действие будет аналогично умножению на 1000, 100, 10 (так как дробь, на которую делим переворачивается).
Чтобы найти ответ в подобных задачах, мы переносим запятую на одну, две, три цифры вправо (в зависимости от числа, на которое делим) и дописываем нули, если цифр в числе окажется недостаточно.
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Вот как поступим со смешанным числом: записываем его в виде неправильной дроби, десятичную — в виде обычной дроби и делим по уже стандартной схеме.
Деление десятичных дробей: правила, примеры, решения
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
Решение
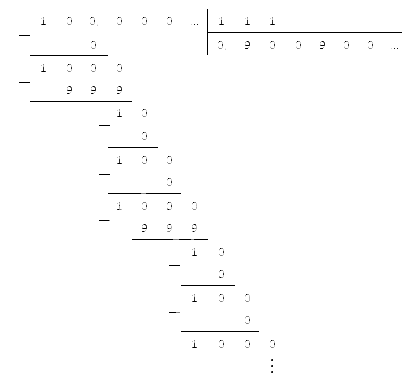
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
Точность результата будет зависеть от степени округления.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Решение
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Решение
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Деление в столбик.
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида 
Например, если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком.
Как делить в столбик лучше всего объяснить на примере. Вычислить :
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2) ).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое «промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Значит, 1976 : 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Десятичные дроби онлайн. Перевод десятичных дробей в обычные и обычных дробей в десятичные.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить поразрядное деление и получить в частном десятичную дробь.
Например, 64 разделим на 5.
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего, меньшего разряда и продолжать деление.
Десятичные дроби
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
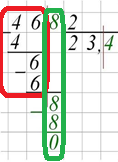
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
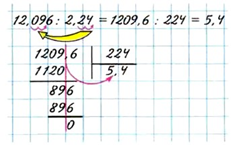
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304
pазбирался: Даниил Романович | обсудить разбор | оценить
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик, тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить