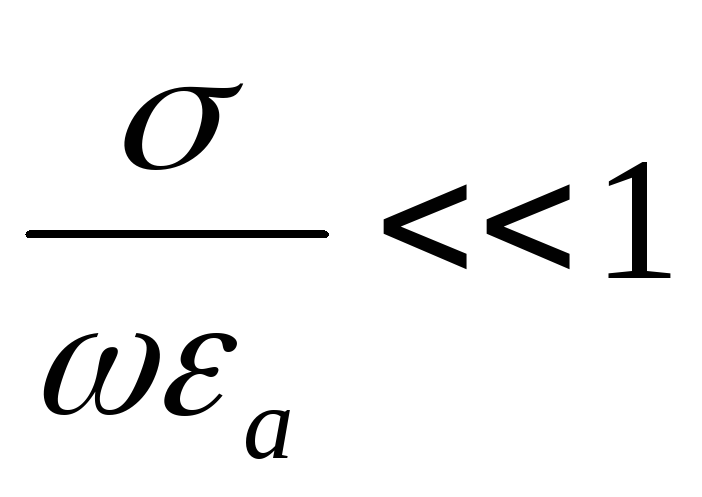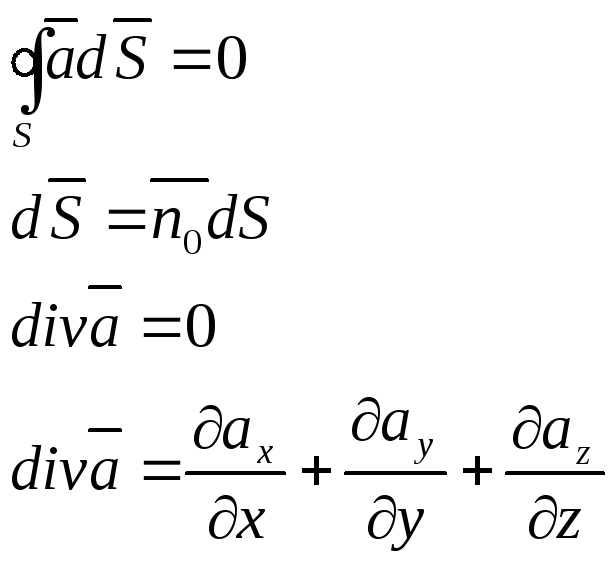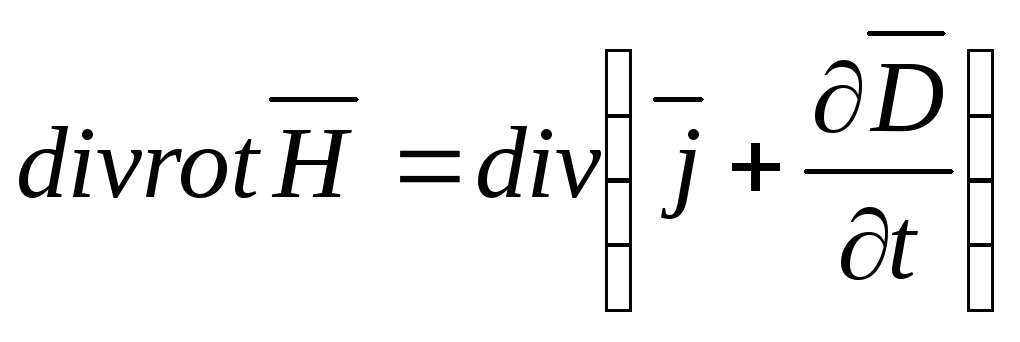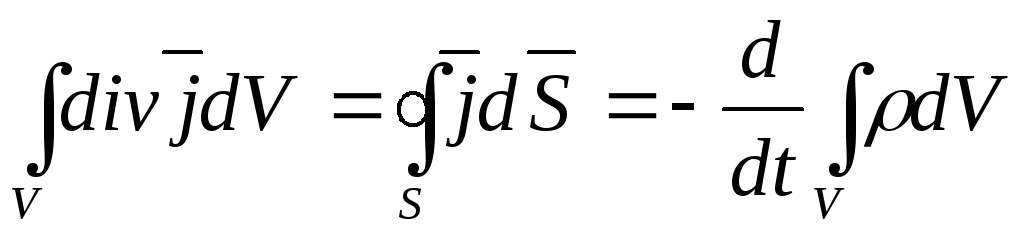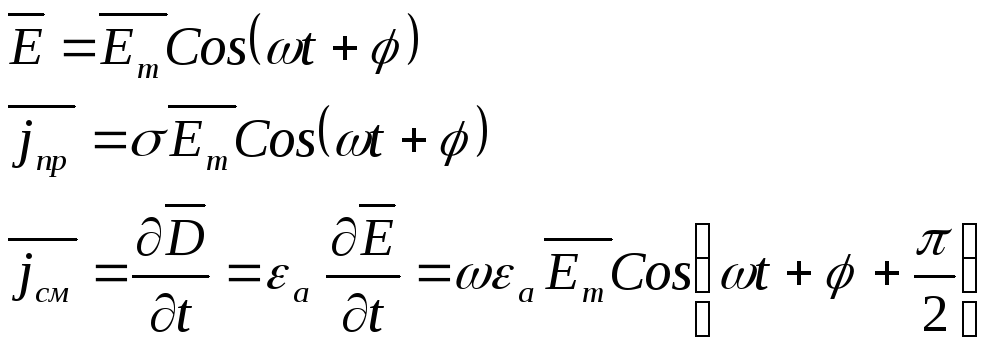вихревое и потенциальное поле

Потенциальное и вихревое поле

Различают два основных типа векторных полей: потенциальные (безвихревые) и вихревые (соленоидальные) поля. Физические свойства их различны.

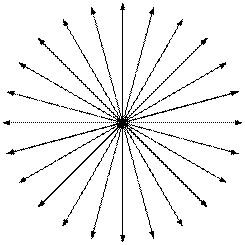
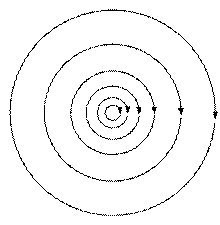
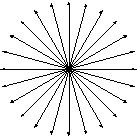
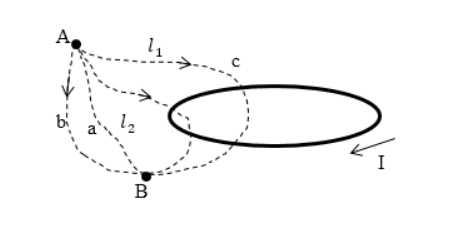
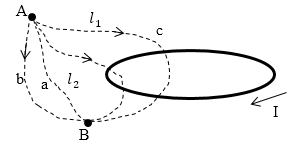
Потенциальное поле тесно связано со своим источником, линии поля имеют начало (исток) и конец (сток). Линии вихревого поля всегда непрерывны и не имеют источников (рисунок 12).

Рисунок 12 − Потенциальное и вихревое поля

Для потенциального поля имеем

,

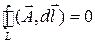
то есть циркуляция вектора по любому замкнутому контуру равна нулю.

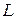
Если поле является вихревым, то поток вектора через любую замкнутую поверхность равен нулю:

.

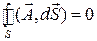
В дальнейшем будет показано, что электростатическое поле является только потенциальным, магнитное – вихревым.

Дата добавления: 2015-10-19 ; просмотров: 5427 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Потенциальное и вихревое поле

Различают два основных типа векторных полей: потенциальные (безвихревые) и вихревые (соленоидальные) поля. Физические свойства их различны.

Потенциальное поле тесно связано со своим источником, линии поля имеют начало (исток) и конец (сток). Линии вихревого поля всегда непрерывны и не имеют источников (рисунок Рисунок 12 ).

−Потенциальное и вихревое поля

Для потенциального поля имеем

,

то есть циркуляция вектора по любому замкнутому контуруравна нулю.

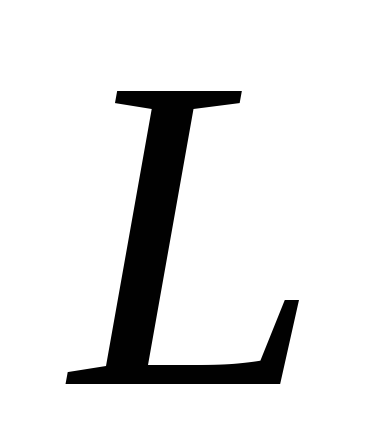
Если поле является вихревым, то поток вектора через любую замкнутую поверхность равен нулю:

.

В дальнейшем будет показано, что электростатическое поле является только потенциальным, магнитное – вихревым.

Градиент, оператор Гамильтона

Далее мы рассмотрим некоторые дифференциальные операции с векторыми и скалярными полями, а именно градиент, дивергенцию (расхождение) и ротор (вихрь). Эти операции потребуются нам при рассмотрении уравнений Максвелла.

Каждое поле порождает собой еще три поля, которые мы и будем рассматривать: векторные поля градиента и ротора и скалярное поле дивергенции.

Градиентом скалярного поля называется вектор, имеющий направление быстрейшего увеличенияи по величине равный производной по этому направлению.

В векторном анализе часто удобно использовать условный вектор, т.н. оператор Гамильтона. В декартовых координатах он имеет вид

.

Тогда можно записать

.

Градиент совпадает по направлению с нормалью к поверхности уровня и направлен в ту сторону, кудавозрастает (рисунок Рисунок 13 ).

Градиент будет применяться при анализе потенциальных векторных полей. Другое применение вектора градиента – численная оптимизация функций.

Дивергенция, физический смысл дивергенции

Для анализа явлений, происходящих в электромагнитном поле, важно знать, где находятся источники того или иного вектора. За меру источника можно выбрать поток вектора через замкнутую поверхность, но внутри данной замкнутой поверхности могут быть источники разных знаков, взаимно уничтожающие свое действие. Чтобы выявить распределение источников в пространстве, можно устремить эту замкнутую поверхность к нулю, но тогда поток вектора через эту бесконечно малую поверхность будет бесконечно малым. Это затруднение ликвидируется тем, что поток вектора через замкнутую поверхность делят на объем, окруженный этой поверхностью. Устремляя объем к нулю, получим предел этого отношения, который и называется дивергенцией.

Дивергенция дает возможность точно указать, в каких точках пространства расположились источники вектора.

Возьмем какую-либо точку поля , окружим ее малым объемоми вычислим поток векторачерез поверхность, ограничивающую объем. Разделим этот поток на, чтобы отнести его к единице объема и перейдем к пределу, устремляя к нулю все размеры, что мы будем обозначать символом. При этом объембудет стягиваться к точке. В результате получится некоторое число, зависящее от поведениявблизи точки, и характеризующее степень истечения из точки. Это число называется расхождением, или дивергенцией векторав точке. Дивергенция обозначается символом. Таким образом,

В векторном анализе доказывается, что

или, с применением оператора Гамильтона,

,

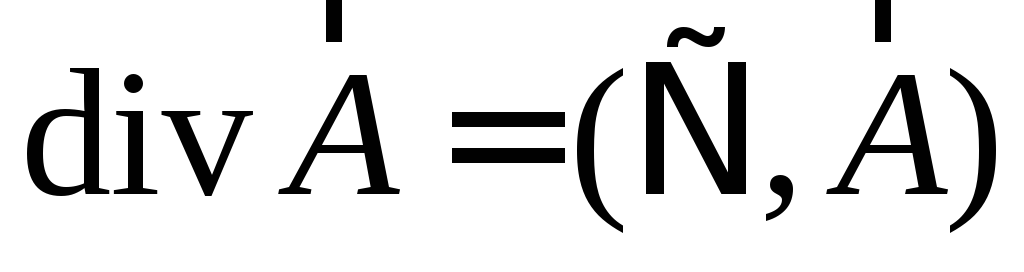
т.е., скалярное произведение оператора набла на вектор .

Рассмотрим значения дивергенции для разных случаев поля (рисунок Рисунок 14 ).

При положительной в точке дивергенции внутри областипоток векторачерез ограничивающую поверхность больше нуля, то есть линии вектора расходятся из этой области. Таким образом, внутринаходятся источники вектора. При отрицательной дивергенции, наоборот, линии вектора сходятся в областьи тогда внутри нее находятся стоки векторного поля.

Если же во всех точках некоторой области поля дивергенция оказывается равной нулю, что силовые линии поля либо пронизывают ее, либо являются замкнутыми.

Источник

Вихревой характер магнитного поля

Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.

Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.

Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:

Определение вихревого поля также выполнимо другим способом.

Вихревое магнитное поле

Векторные поля, вектор которых не равен нулю – это вихревые магнитные поля.

Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:

При отсутствии токов вектор магнитной индукции B → представляется в виде градиента скалярного магнитного потенциала φ m :

Если имеются токи, то данное представление невозможно.

Различие между потенциальными и вихревыми полями

Основными уравнениями магнитного поля постоянных токов считаются выражения вида:

Произведем сравнение с основными уравнениями электростатики:

Магнитное поле считается вихревым при наличии токов. Оно зависит от формы контура и не определяется только положением начала и конца этого контура. Существование однозначной разности потенциалов в магнитном поле исключено. Значение магнитного напряжения по замкнутому контуру не равняется нулю.

Известно значение r o t :

Ответ: Вспомнив теорему о циркуляции, получаем отсутствие токов. В данном случае, представление вектора индукции магнитного поля невозможно в виде магнитного потенциала в области, где проходят токи.

Следует задать нулевой потенциал в точке В :

Источник

Вихревой характер магнитного поля

Вы будете перенаправлены на Автор24

Определения вихревого поля Отсутствие магнитных зарядов

Линии индукции любого магнитного поля непрерывны, у них нет начала и конца, они либо замкнуты, либо уходят в бесконечность и совершенно не важно, какими контурами с током порождаются эти поля. Векторные поля, которые обладают непрерывными силовыми линиями, называются вихревыми полями. И так, магнитное поле является вихревым.

Электростатические поля имеют силовые линии, которые начинаются и заканчиваются на электрических зарядах, они всегда разомкнуты. Линии магнитного поля, напротив, всегда замкнуты, что означает, что магнитных зарядов в природе не существует.

Движение электрических зарядов образует электрический ток. Так как магнитных зарядов не существует, то не существует и магнитного тока. Отсутствие магнитных зарядов выражает следующее уравнение:

Можно вихревое поле определить иначе.

Векторные поля, вектор которых не равен нулю, называют вихревыми полями.

Исходя из теоремы о циркуляции в локальном виде:

В том случае, если токов нет, вектор индукции ($\overrightarrow$) можно представить в виде градиента скалярного магнитного потенциала ($<\varphi >_m$):

Надо заметить, что при наличии токов такое представление невозможно.

Различие между потенциальными и вихревыми полями

Основными уравнениями магнитного поля постоянных токов являются выражения:

Сравним их с основными уравнениями электростатики:

Готовые работы на аналогичную тему

Задание: Покажите, почему для вихревого магнитного поля не возможно представить вектор индукции ($\overrightarrow$) в виде градиента магнитного потенциала ($<\varphi >_m$).

Допустим, что мы можем записать:

Если подставить (1.3) в (1.2) мы видим, что:

По теореме о циркуляции получается, что токи отсутствуют. Следовательно, представление вектора индукции магнитного поля не возможно в виде магнитного потенциала в области, где текут токи.

Рассмотрим магнитное поле возле контура с током (рис.1). В соответствии с теоремой о циркуляции для любого контура выполняется равенство:

Так как при отсутствии токов магнитное поле становистя потенциальным, интеграл, который берется между точками A и B не зависит от пути интегрирования, то можно записать:

Выражение (2.3) можно рассматривать как разность скалярных магнитных потенциалов в точках A и B. Если поступить, как делалось для потенциала в электростатике, то есть принять, что в какой то точке, например токе B потенциал равне нулю, то запишем:

Однако, если выбрать контур, который будет охватывать какой-либо ток, например контур AcbB (рис.1) в таком случае линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет отличен от нуля:

Зададим нулевой потенциал в точке B, тогда имеем, что:

Источник

Потенциальные и вихревые поля.

Два основных типа векторных полей: потенциальные (или без векторные) и вихревые (или соленоидные) поля.

Потенциальное поле – связано со своим источником, имеет начало (исток) и конец (сток).

Если поле является потенциальным, то ширинапо замкнутому контуру Г равна 0.

Если поле вектора вихревое, то поток векторачерез замкнутую поверхность S равен 0.

Основные уравнения электродинамики.

Впервые опубликованы Максвеллом в 1873 г.

Первое уравнение Максвелла.

Является обобщением закона полного тока (закон Ампера).

Циркуляция Н по замкнутому контуру Г равна току пронизывающему контур:

До Максвелла под током I понимали только ток проводимости. В общем случае:

, где

S – произвольная поверхность, опирающаяся на контур Г.

Максвелл дал обобщенную формулировку закону полного тока. Он ввел понятие тока смещения и предположил, что в случае переменных полей ток смещения с точки образования магнитного поля равен току проводимости. Примером системы, где протекают токи смещения – конденсатор.

Плотность тока смещения:

Второе уравнение Максвелла.

Является обобщением закона индукции Фарадея: если замкнутый контур Г пронизывается переменным потоком Ф, то в контуре возникает ЭДС е, равная скорости изменения магнитного потока.

Считалось, что это уравнение справедливо только для проводящего контура.

Максвелл обобщил на случай непроводящей среды.

ЭДС в замкнутом контуре равна циркуляции Е по контуру.

интегральная форма.

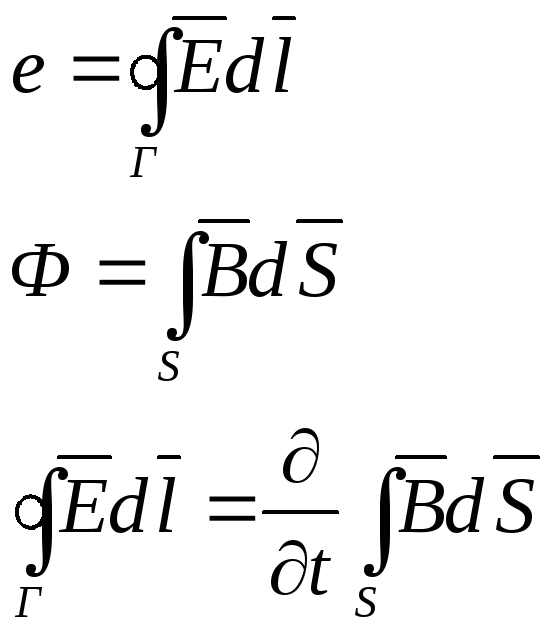
Третье уравнение Максвелла.

Четвертое уравнение Максвелла.

Уравнение непрерывности.

Уравнение непрерывности дает аналитическое выражение закону сохранения заряда. Его можно получить из первого уравнения Максвелла. Возьмем дивергенцию от левой и правой части.

Учитывая, что дивергент ротора любого вектора равен 0, получаем:

Правая часть первого уравнения Максвеллапредставляет собой сумму плотностей тока проводимости и тока смещения, т.е. плотность полного тока, так что полученное уравнение эквивалентно условию:

Равенство нулю дивергенции какого-либо вектора означает непрерывность линий этого вектора. Следовательно, линии плотности полного токаявляются непрерывными, в то время как линии токов проводимости и смещения могут иметь начало и конец. Уравнение

тесно связано с законом сохранения заряда. Закон сохранения заряда можно сформулировать следующим образом:Всякому изменению величины заряда, распределенного в некоторой области, соответствует электрический ток I, втекающий в эту область или вытекающий из нее.

это уравнение может быть получено из предыдущего путем интегрирования по объему:

сточки зрения электромагнитных явлений любые среды характеризуются тремя основными параметрами – проводимостью, диэлектрической_аи магнитной_апроницаемостью.

Среды могут сильно отличатся друг от друга по величине удельной проводимости, поэтому их поведение в электромагнитном поле может быть совершенно различным. При среда становится идеальным проводником. При0 – идеальным диэлектриком. В идеальном проводнике может существовать только ток проводимости, в идеальном диэлектрике – толь ток смещения. В реальных средах существуют оба тока. Реальные среды делят на проводники и диэлектрики. Для проводников j_прj_см, для диэлектриков j_прj_см. Такое деление имеет относительный характер, так как в значительной степени зависит от электромагнитного поля. Пусть:

является критерием деления сред на проводники и диэлектрики.

Для проводников для диэлектриков. Свойства среды зависят от частоты. Это отношение носит название тангенс угла диэлектрических потерь tg. Чем больше tgтем больше энергия поля.

Источник