мнимая единица что это

Мнимая единица – число на грани мистики

Человеку не сведущим в математике и физике рассуждения о мнимой единице представляется полным бредом. Например, квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Отсюда ясно, что квадратные корни из отрицательных чисел не могут находиться среди возможных действительных чисел. Следовательно, нам не остается ничего другого, как признать их невозможными числами.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел. Это было сделано китайскими математиками во II веке до н. э. Отрицательные числа не так просты. Представьте, сколько будет 3 – 4? Как можно отнять 4 барана от 3? Отрицательные числа рассматривались как полная чушь. Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число Е и много еще чего, не понимал отрицательные числа так же хорошо, как

мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений. Древнегреческие математики считали «настоящими» только натуральные числа.

То, что называют мнимым числом, на самом деле частный случай комплексного числа. Это число настоящим числом назвать нельзя. Учебники описывают его как величину, которая, будучи возведенной в квадрат, дает минус один. Другими словами, это сторона квадрата с отрицательной площадью. В реальности такого не бывает. Впервые понятие «мнимая величина» использовал Кардано (1545). Он решал задачу с помощью квадратных уравнений

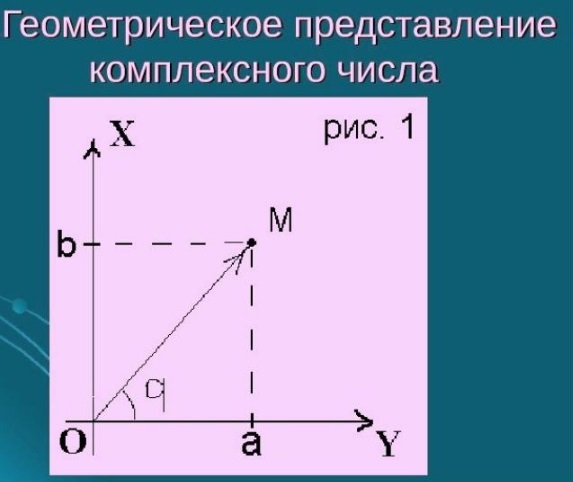
Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс означает связь, сочетание, совокупность понятий, предметов, явлений образующих единое целое. В конце XVIII века, в начале XIX века было получено геометрическое истолкование комплексных чисел. Датчанин К. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изобразить комплексное число z = a + b × i точкой m (a, b) на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой M, а вектором, идущим в эту точку из начала координат. Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения. В дальнейшем Леонард Эйлер (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) получил знаменитую формулу, и открыл комплексным числам дорогу в самые различные области математики и ее приложений.

Комплексные числа – расширили понятие числа. В 1843 году ирландский математик Уильям Гамильтон предложил четырехмерную систему комплексных чисел, которая стала первой гиперкомплексной системой, названную кватернионами. Теория кватернионов вскоре стала одним из источников дальнейшего развития математики и ее приложений.

Значение математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения.

Источник

Откуда есть пошло комплексное число

В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе неочевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей.

Существует распространенное заблуждение, что комплексные числа потребовались для того, чтобы решать квадратные уравнения. На самом деле, это совершенно не так: задача поиска корней квадратного уравнения никоим образом введение комплексных чисел не мотивирует. Вот совершенно.

Давайте убедимся сами. Всякое квадратное уравнение можно представить в виде:
.
Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой и параболы
Я тут даже картинку сделал, для иллюстрации.

Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:

Оказываются возможными 3 варианта:
1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.

В первом случае имеются 2 различных корня, во втором два совпадающих, в третьем уравнение «не решается». Все эти случаи имеют вполне наглядную геометрическую интерпретацию:
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).

Ситуация проста, логична, непротиворечива. Пытаться извлекать квадратный корень из отрицательного числа нет совершенно никаких оснований. Никто и не пытался.

Обстановка существенно изменилась, когда пытливая математическая мысль добралась до кубических уравнений. Чуть менее очевидно, используя некоторую несложную подстановку, всякое кубическое уравнение можно свести к виду: . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
Взгляните на картинку:

Существенное отличие от случая квадратного уравнения в том, что какую бы прямую мы не взяли, она всегда пересечет параболу. Т.е., уже из чисто геометрических соображений, кубическое уравнение всегда имеет хотя бы одно решение.
Найти его можно воспользовавшись формулой Кардано:

где
.
Немного громоздко, но пока, вроде бы, все в порядке. Или нет?

Вообще, формула Кардано — это яркий пример «принципа Арнольда» в действии. И что характерно, Кардано никогда на авторство формулы не претендовал.

Вернемся, однако, к нашим баранам. Формула замечательная, без преувеличение великое достижение математики начала-середины XVI века. Но есть у нее один нюанс.
Возьмем классический пример, который рассматривал еще Бомбелли:
.
Внезапно,
,
и, соответственно,
.
Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.

Идея Рафаэля Бомбелли заключалась в следующем: давайте прикинемся шлангом и сделаем вид, что корень из отрицательного — это какое-то число. Мы, конечно, знаем, что таких чисел нет, но тем не менее, давайте представим, что оно существует и его, как обычные числа, можно складывать с другими, умножать, возводить в степень и т.п.

Используя подобный подход, Бомбелли установил, в частности, что
,
и
.
Давайте проверим:
.
Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.

В сумме получаем . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.

Тем не менее, подобные выкладки выглядят как некоторая магия, математический фокус. Отношение к ним, как к некоему трюку, сохранялось среди математиков еще очень долго. Собственно, придуманное Рене Декартом для корней из отрицательных название «мнимые числа» вполне отражает отношение математиков тех времен к таким развлечениям.

Однако, время шло, «трюк» применялся с неизменным успехом, авторитет «мнимых чисел» в глазах математического общества рос, сдерживаемый, однако, неудобством их использования. Лишь получение Леонардом Эйлером (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) знаменитой формулы

открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.

Источник

Лекция по высшей математике «Мнимая единица. Алгебраическая форма комплексного числа»

Алгебраическая форма комплексного числа.

Цели: расширить понятие числа, ввести понятие мнимой единицы и ее степеней, понятие комплексного числа; рассмотреть алгебраическую форму комплексного числа ; развивать умения обобщать полученные знания, способствовать развитию логического мышления;

воспитывать у обучающихся сознательное отношение к процессу обучения.

Мнимые числа. Определение мнимой единицы. Степени мнимой единицы.

Определение комплексного числа.

Алгебраическая форма комплексного числа.

Например:

Например: и и .

Теорема. Люб ая натуральн ая степень числа і может быть преобразован а к

Пусть m =4 k +3, тогда і м

Пример. Вычислить значение выражения

.

Замечание. Для того, чтобы вычислить степень мнимой единицы, удобно пользоваться таким правилом:

1) разделить показатель степени на 4;

Символически действительную и мнимую части комплексного числа обозначают так: (ре зет), (им зет).

Замечание. Иногда мнимой частью комплексного числа z = а + b і называют bi.

Для комплексных чисел не существует понятий больше и меньше, то есть комплексные числа не сравнимы.

Определение. Комплексное число (-а- bi ) называется противоположным комплексному числу

Определение. Два комплексных числа, у которых действительные части равны, а мнимые

части противоположные, называются комплексно сопряженными числами и

обозначаются соответственно и .

3.Алгебраическая форма комплексного числа. Действия над комплексными числами, заданными в алгебраической форме.

Сложение комплексных чисел

Определение. Суммой двух комплексных чисел и называется

комплексное число .

Итак, (1)

Таким образом, чтобы сложить два комплексных числа нужно сложить их действительные части, и это дает действительную часть суммы, и сложить мнимые части, что дает мнимую часть суммы.

Сумма сопряженных чисел всегда является действительн ым числом

то есть, . (2)

Вычитание комплексных чисел

Определение. Разностью двух комплексных чисел и называется такое

комплексное число , которое в сумме с числом дает число .

Вычитание комплексных чисел всегда возможно.

Теорема. Для любых комплексных чисел и всегда существует разница , которая определена однозначно.

Таким образом, для того, чтобы вычесть комплексные числа, достаточно вычесть их действительные части и их разницу взять за действительную часть разности, а также вычесть мнимую часть разности

Получается, (3)

Разность двух сопряженных чисел всегда является мнимым числом. ,

то есть, (4)

Умножение комплексных чисел

Определение. Произведением двух комплексных чисел и называется такое комплексное число, которое определяется формулой: (5)

В процессе умножения комплексных чисел лучше выполнять непосредственное умножение. Произведение сопряженных чисел всегда является действительным числом

.

Пример. Найти значение выражения .

Решение: .

Деление комплексных чисел

Определение. Частным двух комплексных чисел и называется такое

комплексное число z, которое в произведении с дает .

Всегда существует частное от деления двух комплексных чисел, если знаменатель отличается от нуля.

Теорема. Частное определено и к тому же однозначно для всех комплексных чисел и , если только , то есть .

(7)

Пример. Вычислить значение выражения .

Решение:

Над комплексными числами в алгебраической форме возможно выполнять и такие действия, как возведение в степень, извлечения корня. Но выполнение этих действий в алгебраической форме довольно трудоемкое.

Закрепление изученного материала.

1. Вычислить:

2. Среди приведенных примеров укажите :

а) чисто мнимые комплексные числа;

б) чисто действительные комплексные числа;

в) сопряженные комплексные числа;

г) равные комплексные числа:

3. Выполнить действия: Ответ.

4. На основании равенства комплексных чисел найти действи­тельные числа и если Ответ.

5. Решить квадратные уравнения и проверить выполнение тео­ремы Виета:

а) б) Ответ. а) б)

1.Дать определение комплексного числа.

2.Сформулировать определение мнимой единицы.

3.Как найти степень мнимой единицы.

4.Какие комплексные числа называют равными, сопряженными?

5.Записать формулу для нахождения произвольного степени мнимой единицы.

6. Приведите примеры чисто мнимых чисел.

7. Дать определение суммы, произведения и частного двух комплексных чисел.

Письменный, Д. Т. Конспект лекций по высшей математике: полный курс Д. Т. Письменный. – 9-е изд. – М.: Айрис-пресс, 2009. 608 с.: ил. – (Высшее образование).

Лунгу, К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. – 7-е изд. – М.: Айрис-пресс, 2008. 576 с.: – (Высшее образование).

Григорьев В. П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования / В. П. Григорьев, Ю. А. Дубинский. – 10-е изд., стер. – М. Издательский центр «Академия», 2014. – 320 с.

Источник