метрическая шкала что это
Инструменты и методики сервиса → Метрические шкалы в социологии

Что такое метрическая шкала и как ее правильно применять в анкетах?
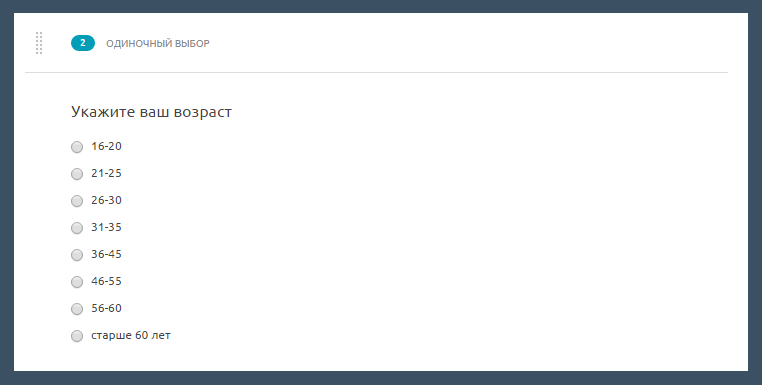
Метрическая шкала в социологии — это непрерывный ряд значений числового показателя. Такая шкала должна давать ответ на вопрос, насколько или во сколько раз различаются значения изучаемого признака у одного респондента в сравнении с другим. Примером метрической шкалы в вашей анкете может стать измерение возраста респондента — в данном случае можно установить, что один из них, скажем, на пять лет моложе или вдвое старше другого. Пример представлен ниже.
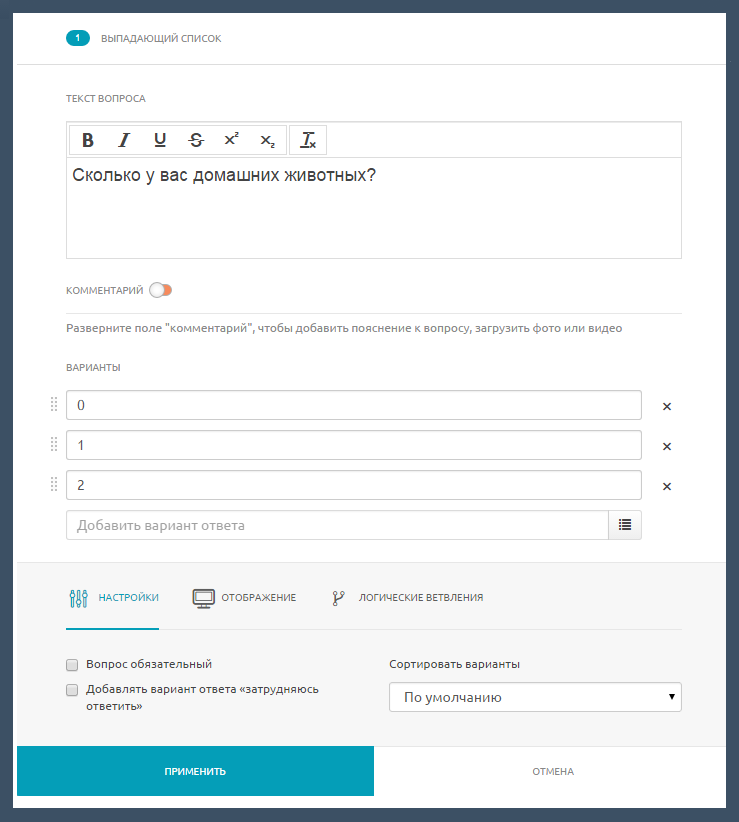
Используя конструктор анкет «Анкетолога», метрическую шкалу можно создать с помощью вопросов «Выпадающий список», «Одиночный выбор» и «Множественный выбор». При этом нужно позаботиться о том, чтобы предлагаемый перечень включал в себя все возможные варианты ответа. Этот способ лучше подходит для вопросов, предполагающих небольшой разброс значений. Пример такой метрической шкалы — вопрос о количестве домашних животных.
Метрическая шкала: пример использования и анализ данных
К метрической шкале в социологии применимы практически любые математические методы анализа данных. Так, имея полный объем информации о размере дохода респондента, можно вычислить любые виды средних значений. К примеру, можно рассчитать средний уровень дохода среди представителей разных профессий или полов. Помимо этого, возможен расчет коэффициента вариации, медианы и прочих стандартных компонентов статистического анализа количественной переменной.
Кроме того, такие данные позволяют использовать более точные методы диагностики взаимосвязи между переменными: например, метрическая шкала в социологии дает возможность рассчитывать коэффициент корреляции Пирсона — выяснить, верно ли, что с увеличением возраста доходы респондентов возрастают.
Наконец, метрические шкалы в социологии — это отличная база для построения так называемой регрессионной модели. Она дает возможность не только установить факт влияния исследуемого признака на зависимую переменную, но и определить степень его влияния. Например, используя метрическую шкалу для сбора данных о доходе респондента, мы можем выяснить, как сильно он влияет на количество детей в его семье.
Провести социологическое, маркетинговое исследование с помощью онлайн-сервиса
Шкала измерений — типы, предел, виды
Шкала измерений – это совокупность значений, позволяющих количественно или качественно отобразить свойства объекта измерений. Разнообразные проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой физической величины. Шкала физической величины — это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений.
Виды шкал измерений
В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства измерительных шкал в метрологии проявляются только качественно, другие — количественно.
Шкала – упорядоченный числовой или символьный ряд значений, отражающий допустимые вариации значений измеряемой величины.
В соответствии с логической структурой проявления свойств различают пять основных видов шкал измерений: шкалы наименований, шкалы порядка, шкалы интервалов, шкалы отношений, абсолютные шкалы.
Элементы шкалы
Интервал деления шкалы (деление шкалы) — расстояние между осями симметрии двух рядом лежащих штрихов (выражается в линейных или в угловых единицах)
ШКАЛЫ ИЗМЕРЕНИЙ
Шкала наименований – это качественная, а не количественная шкала, она не содержит нуля и единиц измерений (напр., шкала цветов).
Такие шкалы используется для классификации объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами ФВ. В шкалах наименований оценивание осуществляется с использованием органов чувств человека, наиболее адекватен результат, выбранный большинством экспертов. Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствуют понятия нуля, «больше или меньше» и единицы измерения.
Шкала порядка – характеризует значение измеряемой величины в баллах (напр., шкала землетрясений; силы ветра и др.).
Она является монотонно изменяющейся и позволяет установить отношения «больше — меньше» между величинами, характеризующими это свойство. Нуль существует или не существует, но принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нельзя судить, во сколько раз больше или меньше конкретные проявления свойства.
Шкала интервалов – имеет условное нулевое значение, а интервалы устанавливают по согласованию (напр., шкала времени, шкала длины).
Данные шкалы являются дальнейшим развитием шкал порядка. Шкала состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летоисчисление, температурные шкалы.
Шкала отношений – имеет естественное нулевое значение, а единица измерений устанавливается по согласованию, в зависимости от требования точности измерения (напр., шкала веса).
С формальной точки зрения эта шкала является шкалой интервалов с естественным началом отсчета. К значениям, полученным по шкале отношений, применимы все арифметические действия, что имеет большое значение при измерении ФВ.
Дата добавления: 2014-02-04; 15002; Опубликованный материал нарушает авторские права? | Защита персональных данных |
Не нашли то, что искали? Воспользуйтесь поиском:
Виды шкал средств измерений
Шкала порядка (рангов)
Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства.
В случаях, когда уровень познания явления не позволяет точно установить отношения, существующие между величинами данной характеристики, либо применение удобно и достаточно для практики, используют условные (эмпирические) шкалы порядка. Условная шкала — это шкала ФВ, исходные значения которой выражены в условных единицах. Пример шкалы порядка — шкала вязкости Энглера, 12-бальная шкала Бофорта для силы морского ветра.
Рисунок — Пример шкалы порядка (шкала Бофорта)
Широкое распространение получили шкалы измерений порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) — не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно,
В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающих размеры. С помощью этих чисел можно найти вероятности, моды, медианы, квантили, однако их нельзя использовать для суммирования, умножения и других математических операция. Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным, о чем свидетельствует рассмотренный пример.
Свойства шкал
Неравномерная шкала омметра
Шкала интервалов (разностей)
Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов — летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)
На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.
Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1
Рисунок – Пример шкалы отношений
При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.
Шкала отношений
Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Пример шкалы отношений — шкала массы (второго рода), термодинамической температуры (первого рода).
В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин.
Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)
Шкалы отношений — самые совершенные. Они описываются уравнением Q = q, где Q — ФВ, для которой строится шкала, — ее единица измерения, q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1/.
Литература
Абсолютные шкалы
Абсолютные шкалы — это шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Примером абсолютной шкалы могут стать шкалы с относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.
Отметим, что шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений — метрическими (материальными). Метрические и абсолютные шкалы относятся к разряду линейных. Практическая реализация шкал измерений в метрологии осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.
Изготовление измерительной шкалы своими руками
Видео о том, как самостоятельно сделать шкалу стрелочного прибора на примере изготовления шкалы амперметра.
Метрические шкалы



Шкалы интервалов (разностей) являются дальнейшим развитием шкал порядка и относятся уже к метрическим шкалам. Шкала состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. На шкалах интервалов по сравнению с неметрическими шкалами установлен масштаб. Здесь происходит сравнение с эталоном. Построение такой шкалы позволяет большую часть свойств существующих числовых систем приписывать числам, полученным на основе субъективных оценок.
Начало отсчёта на шкале интервалов не определено и зависит от выбора размера, с которым производится сравнение. Для обеспечения единства измерений этот размер должен быть общепринятым или установленным законодательно.
Примеры:
— к шкалам интервалов относится летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира (юлианский календарь), либо рождество Христово (григорианский календарь);
Таблица 1.6 – Сравнение температурных шкал
| Описание | Кельвин | Цельсий | Фаренгейт | Ньютон | Реомюр |
| Абсолютный ноль | -273.15 | -459.67 | -90.14 | -218.52 | |
| Температура таяния смеси Фаренгейта (соли и льда в равных количествах) | 255.37 | -17.78 | -5.87 | -14.22 | |
| Температура замерзания воды | 273.15 | ||||
| Средняя температура человеческого тела | 310.0 | 36.8 | 98.2 | 12.21 | 29.6 |
| Температура кипения воды | 373.15 | ||||
| Температура поверхности Солнца |
Шкалы отношений являются самыми совершенными, самыми информативными и самыми распространёнными. На них представлена информация о самих размерах физических величин, в частности об их значениях. Это позволяет решать и на сколько, и во сколько раз один размер больше или меньше другого.
К значениям, полученным по шкале отношений, применимы все арифметические действия, что имеет важное значение при измерении физических величин.
Абсолютные шкалыявляются разновидностью шкал отношений, которые устанавливают однозначное (единственно возможное) соответствие между объектами и числами. Иначе говоря, абсолютные шкалы обладают всеми признаками шкал отношений, но дополнительно имеют естественное однозначное определение единицы измерения и соответственно не зависят от принятой системы единиц измерения.
Примеры:
— коэффициент усиления или затухания, коэффициент трения, коэффициент полезного действия, добротность колебательной системы, вероятность, относительная частота появления события в серии испытаний и т.п., выражаются отвлеченными числами, не зависящими от выбора единиц, а при измерении этих величин не требуется эталонов;
— свойствами относительных величин обладают также геометрические и фазовые углы.
Абсолютная шкала может использоваться для измерения относительных величин. Относительные величины могут выражаться:
— в безразмерных единицах (когда отношение двух одноименных величин равно 1);
Особый интерес представляет группа величин с ограниченными шкалами (такие, как коэффициент полезного действия, вероятность). Их значения могут находиться только в пределах от 0 до 1, причем конечные точки этого диапазона физически бесконечно удалены, недостижимы. На практике это обстоятельство вынуждает перейти к логарифмическим оценкам вблизи этих точек.
Логарифмическая величина представляет собой логарифм безразмерного отношения двух одноименных физических величин. Логарифмические величины применяют для выражения уровня звукового давления, усиления, ослабления, выражения частотного интервала и т.д. Единицей логарифмической величины является бел (Б). Дольной единицей от бела является децибел, равный 0,1 Б.
Метрическая шкала что это
ЛЕКЦИЯ № 15. Измерительные шкалы
Измерительные шкалы (от лат. scala – «лестница») – форма фиксации совокупности признаков изучаемого объекта с упорядочиванием их в определенную числовую систему. Измерительные шкалы представляют собой метрические системы, моделирующие исследуемый феномен путем замены прямых обозначений изучаемых объектов числовыми значениями и отображение пропорций континуального состава элементов объекта в соответствующих числах. Каждому элементу совокупности проявлений свойств изучаемого объекта соответствует определенный балл или шкальный индекс, количественно устанавливающий положение наблюдаемой единицы на шкале, которая охватывает всю совокупность или ее часть, существенную с точки зрения задач исследования. Операция упорядочивания исходных эмпирических данных в шкальные носит название шкалирования. Измерительные шкалы являются главным средством сбора и анализа статистического материала как в прикладных, так и в теоретических исследованиях. Они различаются в зависимости от характера функции, лежащей в основе их построения. В качестве такой функции могут служить: сравнение по признаку убывания или возрастания, ранжирование, оценка интенсивности признака или оценка пропорциональных отношений между признаками. Наиболее общая классификация измерительных шкал предложена С. Стивенсон. В ее основу положен признак метрической детерминированности. Согласно этому признаку шкалы делятся на метрические (интервальные и шкалы отношений) и неметрические (номинативные, шкалы порядка).
1. Номинативные шкалы
Номинативные шкалы (шкалы наименований) устанавливают соответствие признака тому или иному классу. Объекты объединяют в классы на основании какого-либо общего свойства (классы эквивалентности) либо символа (обозначения). Необязательно, чтобы между выявленными классами существовала внутренняя взаимосвязь. Само название «шкала наименований» указывает на то, что значения по шкале играют роль лишь названий классов. Одним из распространенных видов номинативной шкалы является классификация объектов на две группы по принципу «А – не-А» (альтернативные признаки в дихотомической шкале наименований). Конкретными примерами применения такой шкалы являются оценивание ответа испытуемого на пункт опросника в виде утверждения или отрицания, соответствие или несоответствие полученного вида ответа ключу (коду) измеряемого свойства (см. личностные опросники).
Примером оценивания в номинативной шкале могут служить классификация решений тестовой задачи или пункт опросника с задачей закрытого типа.
Из названных городов северней расположен город…
Противоположностью значения «великодушный» является…
Другой простейшей разновидностью номинативной шкалы является перечень или набор каких-либо признаков, группируемых при сборе информации или ее обработке.
Вы предпочитаете проводить досуг…
1) с товарищами и приятелями;
3) в занятиях спортом;
4) в кругу семьи и т. д.
Распределение признаков в классах шкалы наименований можно охарактеризовать путем определения абсолютных и относительных частот встречаемости, возможно также определение модальных и центральных значений в классах. Оценка статистической связи между группами признаков возможна с помощью анализа корреляции (см. корреляция качественных признаков).
Если один из рядов переменных представлен в дихотомической шкале наименований, а другой – в любой иной (интернальной, отношений или порядковой), то применяются коэффициенты корреляции бисериальной. Переменные в дихотомической шкале могут распределяться по нормальному закону или иначе в зависимости от этого выбирают способ расчета коэффициентов корреляции.
В строгом смысле номинативная шкала не является шкалой измерения. Она допускает лишь операцию равенства и неравенства и более или менее дифференцированную классификацию признаков. Вместе с тем в психологических исследованиях и психологической диагностике этот вид измерительных шкал имеет достаточно большое значение, особенно при фиксации качественной информации (например, данных проективных методик при сборе психологического анамнеза и т. д.).
2. Порядковые шкалы
Порядковые шкалы (ординальные) предназначены для расчленения совокупности признаков на элементы, связанные отношением «больше – меньше», и допускают отнесение переменных к группам, упорядоченным (ранжированным) друг относительно друга и представляющим некое системное единство. Порядковые шкалы дают возможность оценить степень выраженности признака. Они содержат не менее трех классов с установленной последовательностью, не допускающей перестановки. Так, между двумя показателями объектов А и В, обладающих признаком X, возможны три вида отношений: ХА = ХB; ХА ‹ ХB; ХА › ХB. Если имеются три объекта A, В, С и между ними установлены отношения ХА ‹ ХB, ХB ‹ ХC, из этого следует, что ХА ‹ ХC. При этом значения разностей между признаками не устанавливаются (шкала неметрическая, единицы измерения отсутствуют). Упорядочивание признаков в ординальной шкале может быть униполярным (при определении классов исходят из степени выраженности измеряемого свойства) и биполярным (в основе разделения лежит ранг степени приближения к одному из противоположных полюсов свойства).
В качестве примера униполярного упорядочивания может быть приведена шкала оценивания качеств внимания: «весьма устойчивое /устойчивое / лабильное / рассеянное». Примером оценивания по биполярному принципу может служить идентификация выраженности свойств между полярными антонимическими характеристиками свойств личностных проявлений:
1) уравновешенный… нестабильный;
2) общительный… замкнутый;
3) подвижный… медлительный.
Порядковые шкалы относятся к числу распространенных в психологической диагностике. В качестве одного из практических приемов оценивания результатов испытуемого по порядковой шкале можно привести модификацию теста «Прогрессивные матрицы Равена», в котором каждый ответ включает три варианта, последовательно приближающихся к правильному. Вариантом применения порядковой шкалы может быть закрытый дифференцированный ответ на пункт опросника:
Бывает, что я никак не могу принять какое-то окончательное решение и упускаю возможность сделать что-то своевременно.
1. Полностью согласен.
2. Пожалуй, могу согласиться.
4. Скорее не согласен.
5. Совершенно не согласен.
Порядковая шкала допускает операции равенства / неравенства и сравнения по интенсивности. По сравнению со шкалой наименований здесь возможны определение медианы распределения, использование коэффициентов ранговой корреляции и сопряженности (см. корреляция качественных признаков).
3. Метрические шкалы
Шкала интервалов относится к метрическим шкалам, в которых элементы упорядочены не только по принципу выраженности измеряемого признака, но и на основе ранжирования признаков по размеру, что выражается интервалами между числами, приписываемыми степени выраженности измеряемого признака.
В шкале интервалов нулевая точка отсчета может устанавливаться произвольно, а величины единиц и направление отсчета могут определяться по избираемым константам.
К разряду шкалы интервалов относятся шкалы стандартного IQ-показателя, Т-баллов, процентилей и другие (см. стандартизация, оценки шкальные). Шкалирование в интервальной шкале составляет основу психометрических измерений.
В шкалах отношений (пропорциональных) числовые значения присваиваются объектам таким образом, чтобы между числами и объектами соблюдалась пропорциональность. Начало отсчета в такой шкале фиксировано. Шкала предусматривает операции равенства / неравенства, больше / меньше, равенства интервалов и равенства отношений.
Примером использования такой шкалы в психологических измерениях может служить шкала порогов абсолютной чувствительности анализатора.
Наряду с делением шкал на метрические и неметрические существует классификация по признаку формы фиксации эмпирических данных, а именно: шкалы вербальные, шкалы числовые и шкалы графические.
В психологической диагностике важным практическим вопросом является оценка надежности, одномерности и обоснованности измерительных шкал. Надежность шкалы определяется на основе анализа устойчивости повторных измерений.
Под валидностью понимается обоснование гипотезы о приспособленности данной шкалы для измерения критериального качества, о полноте его отражения и техническом соответствии самой процедуры шкалирования. Под одномерностью или соразмерностью шкалы понимаются сопоставимость шкалируемых параметров, отсутствие их смещений или пропорциональность между положительными и отрицательными полюсами шкалы, равенство интервалов шкалы или симметричность различных позиций.