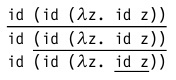лямбда это что в математике

И остатка от деления

[math]\operatorname = \operatorname\ \operatorname[/math]

Проверка на простоту [ править ]

[math]\operatorname = \operatorname\ \operatorname[/math]

Следующее простое число. [math]\operatorname[/math] — следующее, больше либо равное заданного, [math]\operatorname[/math] — следующее, большее заданного.

[math]\operatorname = \operatorname\ \operatorname[/math]

[math]\operatorname[/math] пропрыгает [math]i[/math] простых чисел вперёд. [math]\operatorname[/math] принимает число [math]i[/math] и пропрыгивает столько простых чисел вперёд, начиная с двойки.

Списки [ править ]

Для работы со списками чисел нам понадобятся следующие функции:

[math]\operatorname = \operatorname\ \operatorname\ \bar 1[/math]

[math]\operatorname = \operatorname\ \operatorname[/math]

Выводы [ править ]

На основе этого всего уже можно реализовать эмулятор машины тьюринга: с помощью пар, списков чисел можно хранить состояния. С помощью рекурсии можно обрабатывать переходы. Входная строка будет даваться, например, закодированной аналогично списку: пара из длины и числа, характеризующего список степенями простых. Я бы продолжил это писать, но уже на операции [math]\operatorname[1, 2][/math] я не дождался окончания выполнения. Скорость лямбда-исчисления как вычислителя печальна.

Источник

λ-исчисление. Часть первая: история и теория

Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.

UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.

Вступление

Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)

Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Процесс вычисления

Рассмотрим следующий терм-применение:

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

который для простоты можно переписать как

(напомним, что id — это функция тождества вида λx.x )

В этом терме содержится три редекса:

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Источник

Лямбда-исчисление

А сегодня немного теории. Я не считаю, что лямбда-исчисление является необходимым знанием для любого программиста. Однако, если вам нравится докапываться до истоков, чтобы понять на чем основаны многие языки программирования, вы любознательны и стремитесь познать все в этом мире или просто хотите сдать экзамен по функциональном программированию (как, например, я), то этот пост для вас.

Что это такое

Но речь сегодня не о SQL, а о функциональных языках. Именно для них лямбда-исчисление является основой. Функциональные языки далеко не столь популярны, как, например, объектно-ориентированные, но тем не менее прочно занимают свою нишу. Кроме того, многие идеи из функционального программирования и лямда-исчисления постепенно прокрадываются в другие языки, под видом новых фич.

Если вы изучали формальные языки, то знаете о таком понятии как Машина Тьюринга. Эта вычислительная абстракция определяет класс вычислимых функций. Этот класс столь важен, так как по тезису Черча он эквивалентен понятию алгоритма. Другими словами, любую программу, которую можно запрограммировать на вычислительном устройстве, можно воспроизвести и на машине Тьюринга. А для нас главное то, что лямбда-исчисление по мощности эквивалентно машине Тьюринга и определяет этот же класс функций. Причем создателем лямбда-исчисления является тот самый Алонзо Черч!

Основные понятия

В нотации лямбда-исчисления есть всего три типа выражений:

Сразу пара примеров:

Соглашения

Несколько соглашений для понимания, в каком порядке правильно читать выражения:

Области видимости переменных

Определим контекст переменной, в котором она может быть использована. Абстракция ` lambda x.E ` связывает переменную ` x `. В результате мы получаем следующие понятия:

Вычисление лямбда-выражений

Вычисление выражений заключается в последовательном применении подстановок. Подстановкой ` E’ ` вместо ` x ` в ` E \ ` (запись: ` [E’//x]E ` ) называется выполнение двух шагов:

Функции нескольких переменных

Как результат мы получили функцию от одного аргумента, которая возвращает еще одну функцию от одного аргумента. Такое преобразование называется каррирование (в честь Хаскелла Карри назвали и язык программирования, и эту операцию), а функция, возвращающая другую, называется функцией высшего порядка.

Порядок вычислений

Бывают ситуации, когда произвести вычисление можно несколькими способами. Например, в выражении ` (lambda y. (lambda x. x) y) E ` сначала можно подставлять ` y ` вместо ` x ` во внутреннее выражение, либо ` E ` вместо ` y ` во внешнее. Теорема Черча-Рассера говорит о том, что в не зависимости от последовательности операций, если вычисление завершится, результат будет одинаков. Тем не менее, эти два подхода принципиально отличаются. Рассмотрим их подробнее:

Кодирование типов

В чистом лямбда-исчислении есть только функции. Однако, программирование трудно представить без различных типов данных. Идея заключается в том, чтобы закодировать поведение конкретных типов в виде функций.

Аналогично, с помощью лямбда-исчисления можно выразить любые конструкции языков программирования, такие как циклы, ветвления, списки и тд.

Заключение

Источник

Лямбда-исчисление состоит из построения лямбда-членов и выполнения над ними операций редукции. В простейшей форме лямбда-исчисления термины строятся с использованием только следующих правил:

Операции восстановления включают:

СОДЕРЖАНИЕ

Объяснение и приложения

История

До 1960-х годов, когда было выяснено его отношение к языкам программирования, лямбда-исчисление было всего лишь формализмом. Благодаря приложениям Ричарда Монтегю и других лингвистов к семантике естественного языка лямбда-исчисление стало занимать почетное место как в лингвистике, так и в информатике.

Происхождение символа лямбда

Существует некоторая неопределенность в отношении причины использования Черчем греческой буквы лямбда (λ) в качестве обозначения абстракции функции в лямбда-исчислении, возможно, частично из-за противоречивых объяснений самого Черча. Согласно Кардоне и Хиндли (2006):

Об этом происхождении также сообщалось в [Россер, 1984, с.338]. С другой стороны, в последние годы своей жизни Черч сказал двум вопрошающим, что выбор был более случайным: нужен был символ и просто случайно был выбран λ.

Дана Скотт также обращалась к этому вопросу в различных публичных лекциях. Скотт вспоминает, что однажды он задал вопрос о происхождении лямбда-символа зятю Черча Джону Аддисону, который затем написал своему тестю открытку:

По словам Скотта, весь ответ Черча состоял в том, чтобы вернуть открытку со следующей пометкой : « Ини, миини, мини, мо ».

Неформальное описание

Мотивация

можно переписать в анонимной форме как

можно переписать в анонимной форме как

где ввод просто сопоставляется сам с собой.

Второе упрощение состоит в том, что лямбда-исчисление использует только функции одного входа. Обычная функция, для которой требуются два входа, например, функция, может быть преобразована в эквивалентную функцию, которая принимает один вход, а при выходе возвращает другую функцию, которая, в свою очередь, принимает один вход. Например, s q ты а р е _ s ты м <\ textstyle \ operatorname <квадрат \ _sum>>

может быть переработан в

Функция применения в функции аргументов (5, 2), дает сразу s q ты а р е _ s ты м <\ textstyle \ operatorname <квадрат \ _sum>>

тогда как оценка каррированной версии требует еще одного шага

чтобы прийти к тому же результату.

Лямбда-исчисление

Как описано выше, все функции в лямбда-исчислении являются анонимными функциями, не имеющими имен. Они принимают только одну входную переменную, а каррирование используется для реализации функций с несколькими переменными.

Лямбда-термины

Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически правильных лямбда-терминов:

Ничто иное не является лямбда-термином. Таким образом, лямбда-член действителен тогда и только тогда, когда он может быть получен повторным применением этих трех правил. Однако некоторые скобки можно опустить по определенным правилам. Например, крайние круглые скобки обычно не пишутся. См. Обозначения ниже.

Функции, которые работают с функциями

В лямбда-исчислении функции считаются « значениями первого класса », поэтому функции могут использоваться в качестве входных данных или возвращаться в качестве выходных данных из других функций.

Существует несколько понятий «эквивалентности» и «редукции», которые позволяют «свести» лямбда-термины к «эквивалентным» лямбда-членам.

Альфа-эквивалентность

Для определения β-редукции необходимы следующие определения:

Бесплатные переменные

Замены с избеганием захвата

β-редукция

Формальное определение

Определение

Лямбда-выражения состоят из:

Набор лямбда-выражений Λ можно определить индуктивно :

Обозначение

Чтобы не загромождать нотацию лямбда-выражений, обычно применяются следующие соглашения:

Свободные и связанные переменные

Набор свободных переменных лямбда-выражения M обозначается как FV ( M ) и определяется рекурсией по структуре терминов следующим образом:

Снижение

Значение лямбда-выражений определяется тем, как выражения могут быть сокращены.

Есть три вида сокращения:

α-преобразование

В обозначении индекса Де Брёйна любые два α-эквивалентных термина синтаксически идентичны.

Замена

β-редукция

η-редукция

Нормальные формы и слияние

Однако можно показать, что β-восстановление сливается при работе до α-преобразования (т. Е. Мы считаем две нормальные формы равными, если возможно α-преобразовать одну в другую).

Следовательно, как сильно нормализующие члены, так и слабо нормализующие члены имеют единственную нормальную форму. Для строго нормализующих членов любая стратегия редукции гарантированно дает нормальную форму, тогда как для слабо нормализующих членов некоторые стратегии редукции могут не найти ее.

Кодирование типов данных

Арифметика в лямбда-исчислении

и так далее. Или используя альтернативный синтаксис, представленный выше в Обозначении :

Изменяя то, что повторяется, и варьируя аргумент, к которому применяется эта повторяющаяся функция, можно достичь множества различных эффектов.

PLUS можно рассматривать как функцию, принимающую в качестве аргументов два натуральных числа и возвращающую натуральное число; можно проверить, что

являются β-эквивалентными лямбда-выражениями. Поскольку прибавление m к числу n может быть выполнено добавлением 1 m раз, альтернативное определение:

Точно так же умножение можно определить как

Логика и предикаты

По соглашению для логических значений ИСТИНА и ЛОЖЬ используются следующие два определения (известные как логические значения Черча) :

Затем с помощью этих двух лямбда-терминов мы можем определить некоторые логические операторы (это всего лишь возможные формулировки; другие выражения также верны):

Теперь мы можем вычислять некоторые логические функции, например:

Следующий предикат проверяет, меньше ли первый аргумент второму или равен ему:

Доступность предикатов и приведенное выше определение ИСТИНА и ЛОЖЬ делают удобной запись выражений «если-то-иначе» в лямбда-исчислении. Например, функцию-предшественницу можно определить как:

что позволяет нам дать, пожалуй, наиболее прозрачную версию функции-предшественника:

PRED: = λ n. ПЕРВЫЙ ( n Φ (PAIR 0 0)).

Дополнительные техники программирования

Именованные константы

Объединив такие определения, можно написать «программу» лямбда-исчисления как ноль или более определений функций, за которыми следует один лямбда-член, использующий те функции, которые составляют основную часть программы.

Рекурсия и фиксированные точки

Рассмотрим факториальную функцию F ( n ), рекурсивно определяемую формулой

Самоприложение выполняет здесь репликацию, передавая лямбда-выражение функции следующему вызову в качестве значения аргумента, делая его доступным для ссылки и вызова.

Это решает проблему, но требует перезаписи каждого рекурсивного вызова как самостоятельного приложения. Мы хотели бы иметь общее решение без необходимости переписывать:

Стандартные условия

У некоторых терминов есть общепринятые названия:

Устранение абстракции

Типизированное лямбда-исчисление

Стратегии сокращения

Является ли термин нормализующим или нет, и сколько работы необходимо сделать для его нормализации, если это так, в значительной степени зависит от используемой стратегии сокращения. Общие стратегии сокращения лямбда-исчисления включают:

Слабые стратегии сокращения не сводятся к лямбда-абстракциям:

Стратегии с совместным использованием сокращают количество параллельных вычислений, которые «одинаковы»:

Оптимальное сокращение В обычном порядке, но вычисления с одинаковой меткой сокращаются одновременно. Звоните по необходимости Как вызов по имени (следовательно, слабый), но приложения-функции, которые будут дублировать термины, вместо этого называют аргумент, который затем сокращается только «тогда, когда это необходимо».

Вычислимость

Сложность

Необоснованная модель не обязательно означает неэффективность. Оптимальное сокращение сокращает все вычисления с одной и той же меткой за один шаг, избегая дублирования работы, но количество параллельных шагов β-редукции для приведения данного члена к нормальной форме приблизительно линейно по размеру члена. Это слишком мало, чтобы быть разумной мерой затрат, поскольку любая машина Тьюринга может быть закодирована в лямбда-исчислении в размере, линейно пропорциональном размеру машины Тьюринга. Истинная стоимость сокращения лямбда-членов связана не с β-редукцией как таковой, а с обработкой дублирования редексов во время β-редукции. Неизвестно, являются ли оптимальные реализации сокращения разумными при измерении относительно разумной модели затрат, такой как количество крайних левых шагов к нормальной форме, но для фрагментов лямбда-исчисления было показано, что алгоритм оптимального сокращения эффективен. и имеет не более чем квадратичные накладные расходы по сравнению с крайним левым. Вдобавок реализация оптимального сокращения прототипа BOHM превзошла Caml Light и Haskell по чистым лямбда-терминам.

Лямбда-исчисление и языки программирования

Как указано в статье Питера Ландина 1965 года «Соответствие между АЛГОЛОМ 60 и лямбда-нотацией Черча», последовательные процедурные языки программирования можно понимать в терминах лямбда-исчисления, которое обеспечивает основные механизмы процедурной абстракции и процедуры (подпрограммы) заявление.

Анонимные функции

Например, в Лиспе «квадратная» функция может быть выражена как лямбда-выражение следующим образом:

Параллелизм и параллелизм

Семантика

В 1970-х Дана Скотт показала, что, если бы рассматривались только непрерывные функции, можно было бы найти набор или область D с требуемым свойством, тем самым предоставив модель лямбда-исчисления.

Эта работа также легла в основу денотационной семантики языков программирования.

Варианты и расширения

Эти расширения находятся в лямбда-кубе :

Эти формальные системы являются расширениями лямбда-исчисления, которых нет в лямбда-кубе:

Эти формальные системы представляют собой разновидности лямбда-исчисления:

Эти формальные системы связаны с лямбда-исчислением:

Смотрите также

Примечания

использованная литература

дальнейшее чтение

Монографии / учебники для аспирантов:

Источник