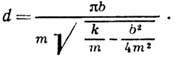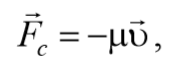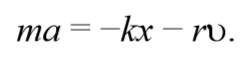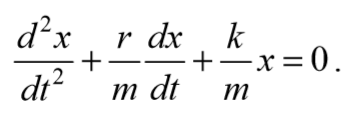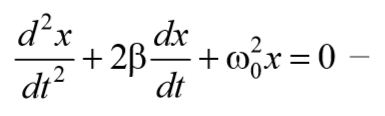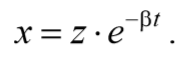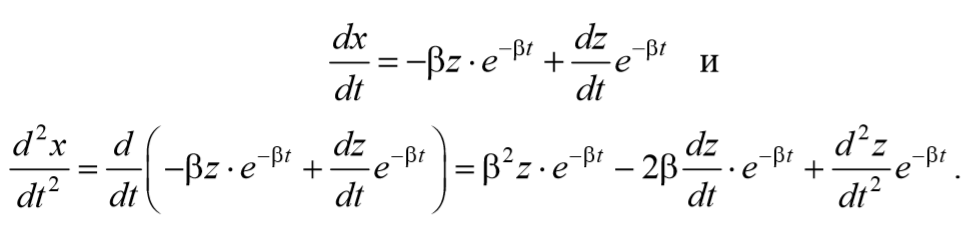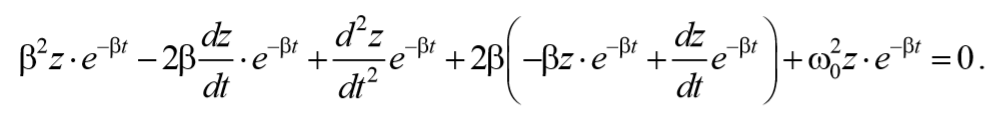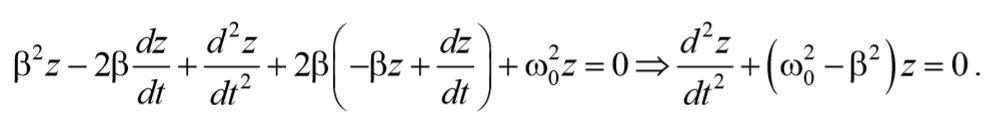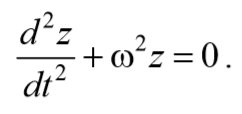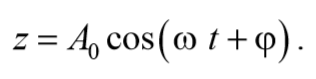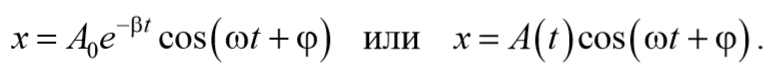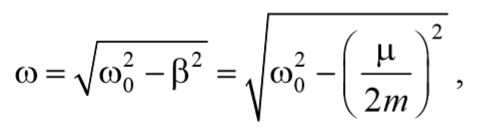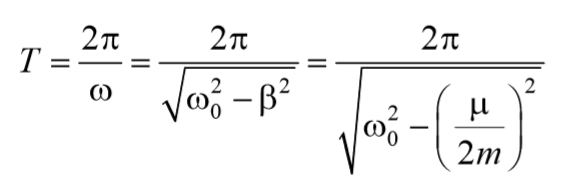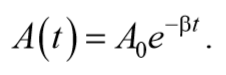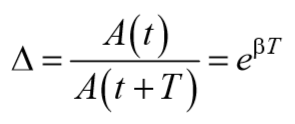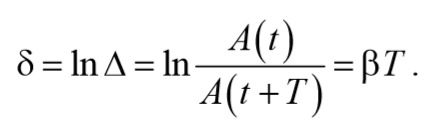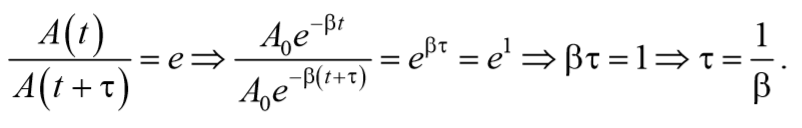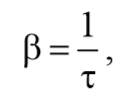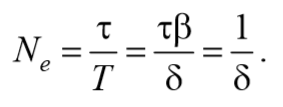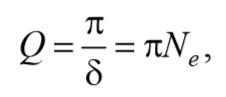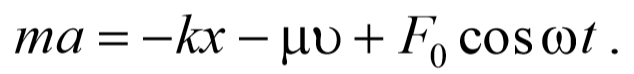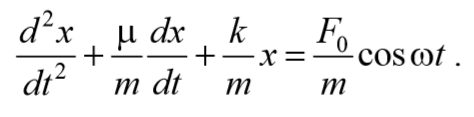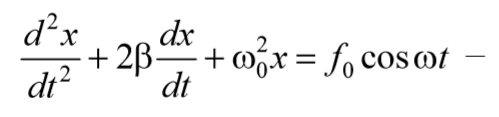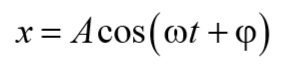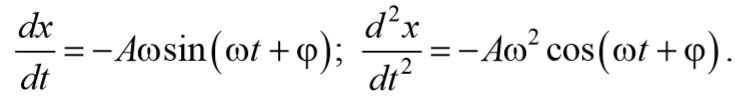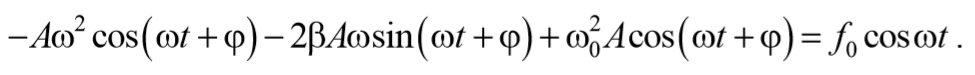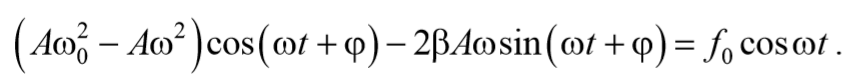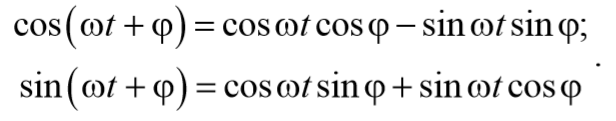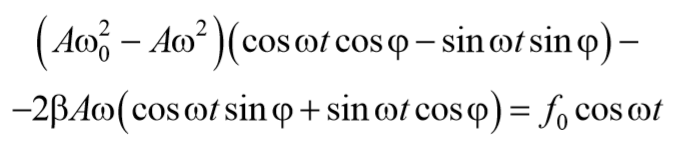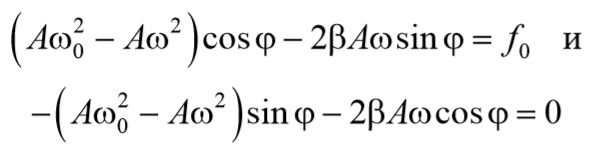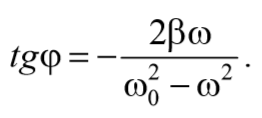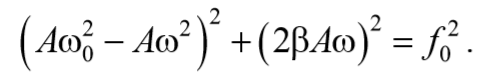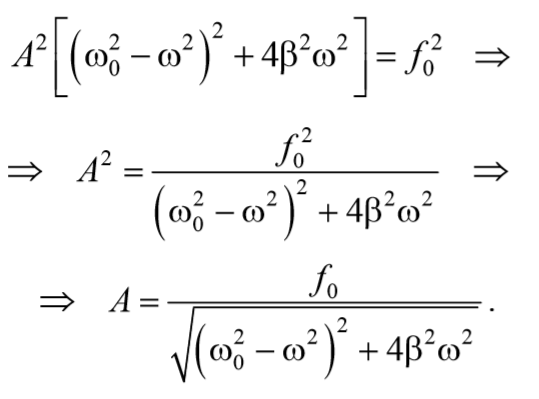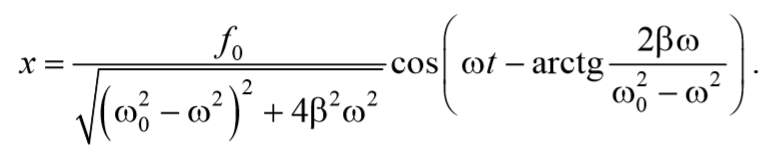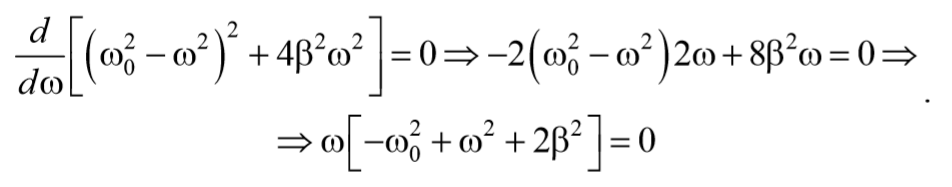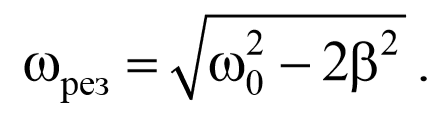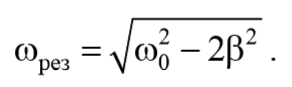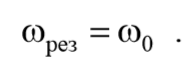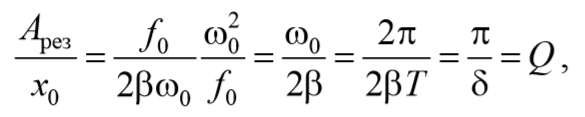логарифмический декремент в чем измеряется
ДЕКРЕМЕНТ ЗАТУХАНИЯ
При малом затухании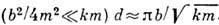 
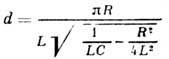
. Аналогично для электрич. контура, состоящего из индуктивности L, активного сопротивления R и ёмкости С, Д. з.
.
При малом затухании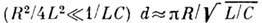 
.
Для нелинейных систем закон затухания колебаний отличен от закона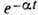 
, т. е. отношение двух последующих «амплитуд» (и логарифм этого отношения) не остаётся постоянным; поэтому Д. з. не имеет такого определ. смысла, как для систем линейных.
Полезное
Смотреть что такое «ДЕКРЕМЕНТ ЗАТУХАНИЯ» в других словарях:
ДЕКРЕМЕНТ ЗАТУХАНИЯ — (от лат. decrementum уменьшение) характеристика быстроты затухания колебаний: d = ln(A1/A2), где А1 и А2 амплитуды двух колебаний, следующих друг за другом в одну и ту же сторону … Большой Энциклопедический словарь
ДЕКРЕМЕНТ ЗАТУХАНИЯ — (Decrement) величина, характеризующая постепенное затухание колебаний. Д. равен отношению двух амплитуд, следующих одна за другой через один период. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза… … Морской словарь
декремент затухания — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN damping decrement … Справочник технического переводчика
декремент затухания — (от лат. decrementum уменьшение), количественная характеристика быстроты затухания колебаний в линейной системе: Δ = ln(А1/А2), где А1 и А2 два последующих максимальных отклонения колеблющейся величины в одну и ту же сторону. * * * ДЕКРЕМЕНТ… … Энциклопедический словарь
декремент затухания — slopimo dekrementas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiantis virpesių amplitudės sumažėjimą per vieną periodą. atitikmenys: angl. damping ratio vok. Dämpfungsverhältnis, n rus. декремент затухания, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
декремент затухания — slopinimo dekrementas statusas T sritis automatika atitikmenys: angl. damping decrement; damping ratio vok. Dämpfungsbeiwert, m; Dämpfungsdekrement, n; Dämpfungsgrad, m; Dämpfungsverhältnis, n rus. декремент затухания, m; относительное затухание … Automatikos terminų žodynas
декремент затухания — slopimo dekrementas statusas T sritis automatika atitikmenys: angl. attenuation decrement; attenuation ratio vok. Dämpfungsgrad, m; Dämpfungsmaß, n rus. декремент затухания, m pranc. décrément d affaiblissement, m … Automatikos terminų žodynas
декремент затухания — slopinimo dekrementas statusas T sritis fizika atitikmenys: angl. damping decrement vok. Dämpfungsdekrement, n rus. декремент затухания, m pranc. décrément d’amortissement, m … Fizikos terminų žodynas
декремент затухания — rus коэффициент (м) звукопоглощения, коэффициент (м) затухания (звука); коэффициент (м) демпфирования; декремент (м) затухания eng damping coefficient, damping factor fra coefficient (m) d amortissement (m) deu Dämpfungsfaktor (m),… … Безопасность и гигиена труда. Перевод на английский, французский, немецкий, испанский языки
Декремент затухания — количественная характеристика быстроты затухания колебаний. Д. з. δ равен натуральному логарифму отношения двух последующих максимальных отклонений х колеблющейся величины в одну и ту же сторону: Д. з. величина, обратная… … Большая советская энциклопедия
Логарифмический декремент колебаний
Логарифмический декремент колебаний — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины в одну и ту же сторону:
Логарифмический декремент колебаний равен декременту, умноженному на период колебаний:
Полезное
Смотреть что такое «Логарифмический декремент колебаний» в других словарях:
логарифмический декремент колебаний — логарифмический декремент Ндп. логарифмический декремент затухания Натуральный логарифм отношения двух последовательных максимальных или минимальных значений величины при затухающих свободных колебаниях. Пояснения 1)Некоторые величины и… … Справочник технического переводчика
Логарифмический декремент колебаний — 107. Логарифмический декремент колебаний Логарифмический декремент Ндп. Логарифмический декремент затухания Натуральный логарифм отношения двух последовательных максимальных или минимальных значений величины при затухающих свободных колебаниях… … Словарь-справочник терминов нормативно-технической документации
Логарифмический декремент затухания — D Величина, показывающая скорость затухания собственных колебаний и определяемая как натуральный логарифм отношения следующих друг за другом амплитуд колебаний Источник … Словарь-справочник терминов нормативно-технической документации
логарифмический декремент — logarithmic decrement Натуральный логарифм отношения двух любых последовательных одинакового знака максимальных амплитуд при затухании одночастотных колебаний. Шифр IFToMM: 3.9.38 Раздел: КОЛЕБАНИЯ В МЕХАНИЗМАХ … Теория механизмов и машин
ДЕКРЕМЕНТ ЗАТУХАНИЯ — (от лат. decrementum уменьшение, убыль), количественная хар ка быстроты затухания колебаний. Д. з. d равен натуральному логарифму отношения двух последующих макс. отклонений х колеблющейся величины в одну и ту же сторону: d=ln(x1/x2). Д. з.… … Физическая энциклопедия
ДЕКРЕМЕНТ ЗАТУХАНИЯ — логарифмический (от лат. decrementum уменьшениеубыль) количеств. хар ка затухания колебаний в линейной системе. Д. з. равен натур. логарифму отношения двух последовательных Макс. отклонений колеблющейся величины в одну и ту же сторону … Большой энциклопедический политехнический словарь
Затухание колебаний — характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто носит колебательный характер … Энциклопедия техники
затухание колебаний — затухание колебаний характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто… … Энциклопедия «Авиация»
затухание колебаний — затухание колебаний характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто… … Энциклопедия «Авиация»
Затухание колебаний — уменьшение интенсивности колебаний с течением времени, обусловленное потерей энергии колебательной системой. Простейшим случаем убыли энергии колебания является превращение её в тепло вследствие трения в механических системах и… … Большая советская энциклопедия
Логарифмический декремент в чем измеряется
Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и 
(рис. 3.1):
,
где β – коэффициент затухания.
Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
;
.
Выясним физический смысл χ и β.
Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.
отсюда 
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.
Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда
; 
;
.
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
Если χ = 0,01, то N = 100.
При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому 
, а 
то круговая частота обращается в нуль ( 
), а ( 
), колебания прекращаются. Такой процесс называется апериодическим (рис. 3.2).
Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.
Лекция №8. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.6. Затухающие гармонические колебания.
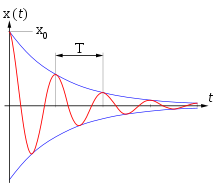
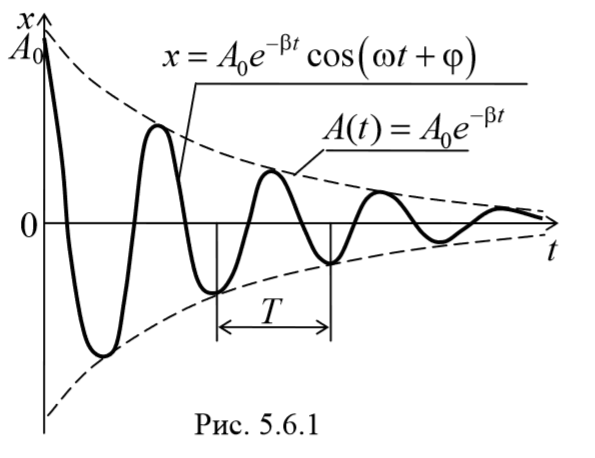
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости
где μ − постоянная, называемая коэффициентом сопротивления.
Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид
Для решения уравнения (5.6.4) сделаем подстановку
Проведем замену переменных
Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)
Решение уравнения (5.6.8) можно записать в виде
Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)
В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой
и амплитудой, изменяющейся по закону
5.7. Коэффициент затухания и логарифмический декремент затухания.
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно
т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.
Для характеристики колебательной системы используется величина
которая называется добротностью колебательной системы.
5.8. Вынужденные колебания.
дифференциальное уравнение вынужденных колебаний.
Будем искать решение уравнения (5.8.3) в виде
предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.
Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)
Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.
Из выражения (71) получаем
Возведем в квадрат уравнения (70) и сложим
Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний
5.9. Резонанс.
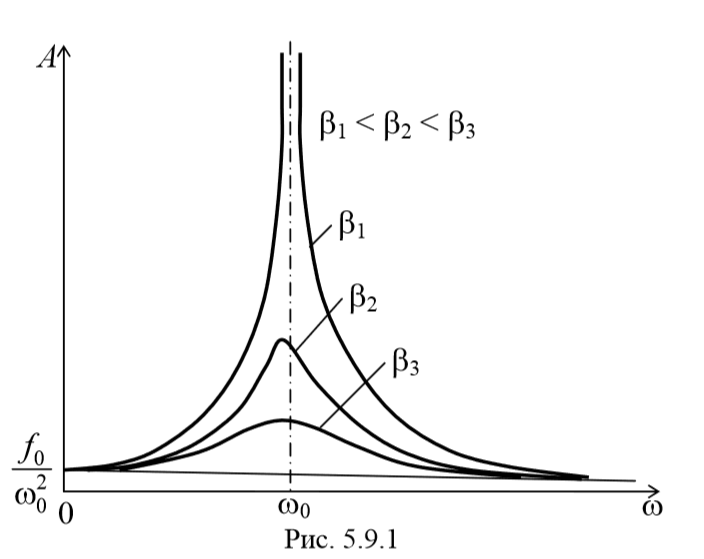
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.
Продифференцируем это выражение по ω и приравняем к нулю
Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе
Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0 ), совпадала бы с собственной частотой колебаний системы ω0
При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.
где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).
Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.
Физика Б1.Б8.
Электронное учебное пособие по разделу курса физики Механика
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
Введение
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.
Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).
Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.
Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.
Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.
Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.
Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.