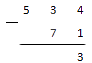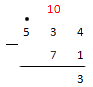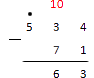Как правильно вычитать столбиком трехзначные числа
Вычитание столбиком. Правила вычитания в столбик.
Чтобы найти разность методом «вычитание столбиком» (другими словами, как считать в столбик или столбиком вычитание), необходимо следовать таким шагам:
Ниже рассмотренные примеры покажут вам как происходит вычитание двухзначных, трехзначных и любых многозначных чисел столбиком.
Вычитание чисел в столбик очень помогает при вычитании больших чисел (как и сложение в столбик). Лучше всего научиться на примере.
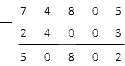
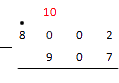
Необходимо записать числа одно под другим таким образом, чтобы крайняя правая цифра 1-го числа стала под крайней правой цифрой 2-го числа. Число, которое больше (уменьшаемое) записываем сверху. Слева между числами ставим знак действия, здесь это «-» (вычитание).
Вычитать нужно с крайней правой цифры. Вычитаем по одной цифре (знаку).
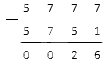
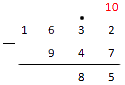
Далее необходимо вычесть из тройки 9. Это невозможно. Значит нужно занять десяток у цифры слева от тройки. Это четыре. Ставим над 4 точку. Занятый десяток прибавим к тройке.
Из 13 вычтем девять.
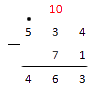
Так как мы заняли десяток у четверки, то она уменьшилось на 1. Для того, чтобы не забыть об этом у нас и стоит точка.
Вычитание столбиком из чисел, содержащих нули.
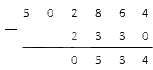
Опять же, разберем на примере:
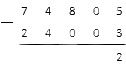
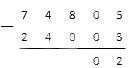
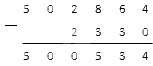
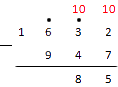
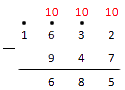
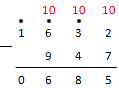
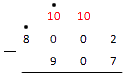
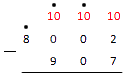
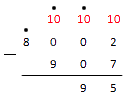
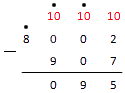
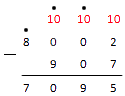
Из нуля вычесть 2 не получится, тогда опять занимаем у цифры слева. Это нуль. Ставим над нулем точку. И снова, у нуля занять не получится, тогда двигаемся дальше к следующей цифре. Занимаем у единицы. Ставим над ней точку.
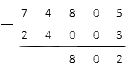
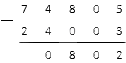
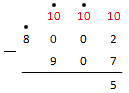
Обратите внимание: когда в вычитании столбиком над 0 есть точка, нуль становится девяткой.
Алгоритм письменного вычитания
Урок 46. Математика 3 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Алгоритм письменного вычитания»
Вы готовы к новым свершениям? Сегодня я предлагаю вам научиться выполнять вычитание столбиком. И, конечно, для этого нам необходима специальная разлиновка в клеточку. Ну-с, приступим.
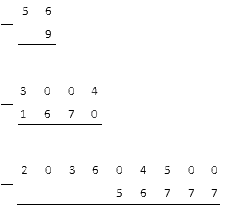
Начнём мы с того, что вспомним вычитание двузначных чисел. Вычтем из шестидесяти семи сорок пять. Обязательно для каждой цифры необходима отдельная, персональная клеточка. Единицы пишем под единицами, а десятки под десятками. Минус. Черта. Вычитаем единицы. Семь минус пять – два. Записываем под единицами. Вычитаем десятки. Шесть десятков минус четыре десятка – два десятка. Ответ: двадцать два.
Но это простейшее вычисление. Его даже устно нетрудно выполнить.
Следующее числовое выражение: Восемьдесят пять минус тридцать девять. Аккуратно записали числа. Вычитаем единицы и так как из меньшего числа большее не вычтешь, надо в разряде десятков занять один. А чтобы случайно не забыть об этом, над разрядом десятков ставим точку-напоминалочку. Один десяток – это десять единиц. Да ещё у нас пять единиц – всего пятнадцать единиц. Теперь девять вычитаем из пятнадцати, получается шесть. Записываем под единицами. Вычитаем десятки. Точка над десятками напоминает о том, что один десяток мы передали единицам. И теперь у нас стало не восемь десятков, а семь. Из семи десятков вычитаем три десятка, остаётся четыре десятка. Ответ: сорок шесть.
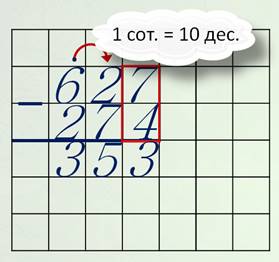
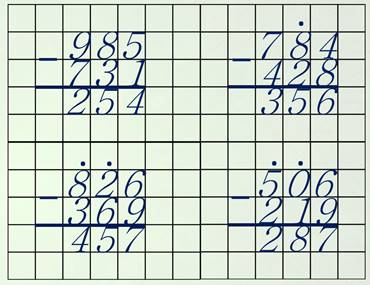
Ну что, вспомнили вычитание двузначных чисел? Переходим к вычитанию трёхзначных. Например, найдём разность чисел шестьсот двадцать семь и двести семьдесят четыре.
Здесь не только единицы пишем под единицами и десятки под десятками, но и сотни – под сотнями.
Но, как всегда, вычитание начинаем обязательно с единиц. Семь минус четыре – три. Два десятка минус семь десятков. Стоп! Разве из меньшего числа большее можно вычитать? Как вы думаете, что надо сделать? Ну, конечно, занимаем одну сотню и превращаем её в десятки. И ставим над сотнями точку-напоминалочку. Одна сотня – это десять десятков. Да ещё два десятка – двенадцать десятков. Минус семь десятков – пять десятков.
Пришло время вычитать сотни. Так как над шестёркой стоит точка, значит, сотен на одну меньше – пять. Пять сотен минус две сотни – три сотни. Ответ: триста пятьдесят три.
Ну, а если из девятисот двадцати трёх вычесть четыреста сорок четыре?
Записываем аккуратно числа и вычитаем. Конечно, начинаем с единиц. Три минус четыре. Занимаем десяток и ставим точку. Тринадцать минус четыре – девять. Точка подсказывает, что у нас остался только один десяток. А вычесть надо четыре десятка. Занимаем одну сотню. Это десять десятков, да ещё один – одиннадцать десятков. Вычитаем четыре десятка – получилось семь десятков. Над сотнями стоит точка, значит их не девять, а восемь. Вычитаем четыре сотни – получилось четыре сотни. И ответ: четыреста семьдесят девять.
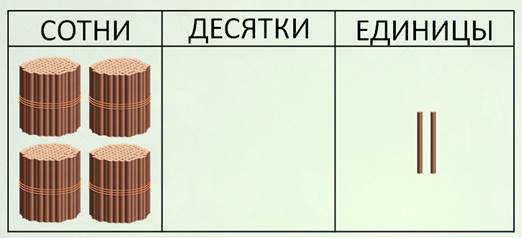
Давайте разберём ещё один пример. Найдём разность чисел четыреста два и сто двадцать пять. Вычитаем единицы. Из двух пять вычесть нельзя. Занимаем один десяток. Ой, а десятков-то и нет. Что делать? Придётся обратиться за помощью к таблице и счётным палочкам. Вот число четыреста два.
Из двух надо вычесть пять. Так как десятков нет, занимаем одну сотню. В примере над сотнями ставим точку. Одна сотня это десять десятков, один из которых мы тоже забираем и передаём к единицам. И над десятками, конечно, тоже стоит точка. Единиц стало двенадцать. Вычитаем пять – остаётся семь. Посмотрите, теперь у нас есть девять десятков. Вычитаем два десятка. Получилось семь десятков. У нас осталось три сотни. Вычитаем одну, осталась две сотни. Ответ: двести семьдесят семь.
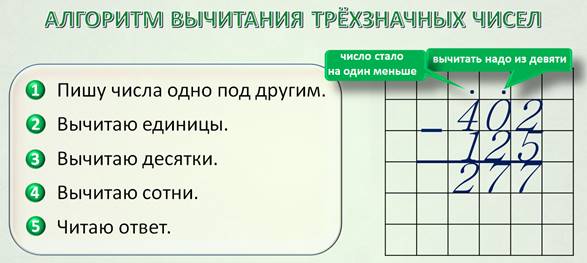
Обратите внимание, если при вычитании в уменьшаемом в разряде десятков стоит нуль, мы над ним ставим точку, а потом точку ставим ещё и над сотнями. Точка над любым числом подсказывает нам, что теперь это число стало на один меньше, а вот точка над нулём говорит о том, что вычитать надо из девяти.
Ну, вам всё понятно? Давайте проверим. Но прежде составим алгоритм вычитания трёхзначных чисел.
Пишу числа одно под другим. Единицы записаны под единицами, десятки под десятками, сотни под сотнями. Знак минус. Черта.
Вычитаю единицы. Если при вычитании единиц в уменьшаемом не хватает, занимаю один десяток, добавляю к единицам ещё десять, а над десятками ставлю точку.
Вычитаю десятки. Точка, стоящая над десятками, показывает, что их на один меньше. Если при вычитании десятков в уменьшаемом не хватает, занимаю одну сотню, добавляю к десяткам ещё десять, а над сотнями ставлю точку…
Вычитаю сотни. Точка, стоящая над сотнями, показывает, что их на одну меньше.
А ещё я хочу напомнить вам, что иногда в уменьшаемом в разряде десятков стоит нуль, как, например, вот в таком примере.
В таких случаях точку ставим над нулём, а потом ещё и над сотнями – ведь у нуля занять нечего. При этом количество сотен уменьшается на один, а десятки вычитать будем из девяти, ведь один десяток также отдали единицам. Просто запомните маленький секретик: нуль, над которым стоит точка, превращается в девять.
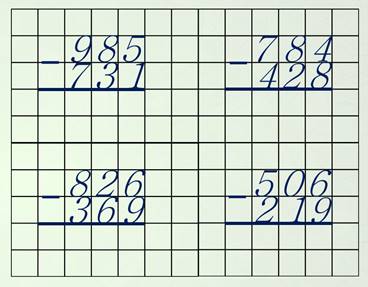
Опираясь на этот алгоритм, я предлагаю вам решить четыре примера.
А потом вместе проверим их решение. Не забудьте ставить точку над цифрами, когда приходится занимать один десяток или одну сотню.
Ну что, проверим, как вы справились с работой?
У вас так получилось? Я думаю, да. А если не всё – не огорчайтесь. Просто поработайте над ошибками, и у вас всё получится. Обязательно!
Ну а нам пришла пора прощаться. До свидания, ребята!
Вычитание столбиком. Правила вычитания в столбик.
Чтобы найти разность методом «вычитание столбиком» (другими словами, как считать в столбик или столбиком вычитание), необходимо следовать таким шагам:
Ниже рассмотренные примеры покажут вам как происходит вычитание двухзначных, трехзначных и любых многозначных чисел столбиком.
Вычитание чисел в столбик очень помогает при вычитании больших чисел (как и сложение в столбик). Лучше всего научиться на примере.
Необходимо записать числа одно под другим таким образом, чтобы крайняя правая цифра 1-го числа стала под крайней правой цифрой 2-го числа. Число, которое больше (уменьшаемое) записываем сверху. Слева между числами ставим знак действия, здесь это «-» (вычитание).
Вычитать нужно с крайней правой цифры. Вычитаем по одной цифре (знаку).
Далее необходимо вычесть из тройки 9. Это невозможно. Значит нужно занять десяток у цифры слева от тройки. Это четыре. Ставим над 4 точку. Занятый десяток прибавим к тройке.
Из 13 вычтем девять.
Так как мы заняли десяток у четверки, то она уменьшилось на 1. Для того, чтобы не забыть об этом у нас и стоит точка.
Вычитание столбиком из чисел, содержащих нули.
Опять же, разберем на примере:
Из нуля вычесть 2 не получится, тогда опять занимаем у цифры слева. Это нуль. Ставим над нулем точку. И снова, у нуля занять не получится, тогда двигаемся дальше к следующей цифре. Занимаем у единицы. Ставим над ней точку.
Обратите внимание: когда в вычитании столбиком над 0 есть точка, нуль становится девяткой.
Вычитаем столбиком с примерами на картинках
Вычитание столбиком с примерами, разберем правило вычитания столбиком. Это очень простая операция, важно понять алгоритм вычитания, а потом сможете решать задачки на вычитание столбиком как семечки!
Вычитание столбиком примеры, правило.
Правило вычитания столбиком.
Первое, наверное с чего нужно начать :
Для того, чтобы вычесть столбиком, существует несколько правил:
Правило вычитания столбиком.
И каждую следующую справа цифру первого числа ставить под следующую цифру второго числа.
Если нижнее(однозначное) число больше верхнего, то занимаем десяток из левого, соседнего верхнего числа.
Если под цифрой сверху, либо снизу нет цифры, то цифру сносим под черту без изменений.
Особенно тяжело понимается третий пункт данного правила(см.выше.)! Поэтому на нём остановимся подробнее!
Нм требуется вычесть два числа столбиком :
Вычитание столбиком подробное описание
Располагаем наши два числа, которые должны вычесть столбцом, по правилам, правая цифра под правой цифрой:
Оставляем зарубку ‘ над числом 3, чтобы не забыть, что мы взяли оттуда единицу!
И последний столбец, под цифрой 8 ничего нет, и мы у восьмерки ничего не занимали, поэтому сносим её под черту без изменений.
Первый простой пример вычитания столбиком:
Для быстрого понимания возьмем простой пример без заимствования десяток…
Равняем по правому краю.
И почему это вычитание называется столбиком, потому, что сейчас.. на картинке вы видите все цифры выстроились в свои столбики.
Теперь в каждом столбике совершаем действие вычитания!
5- 4 =1 – сносим за черту…
3 – 1 = 2 – сносим за черту…
Второй пример вычитания столбиком
Первый пример был очень простым, потому, что все цифры второго числа были меньше чем верхние…
Давайте возьмем другое число и попытаемся отнять столбиком…
Нам потребуется занимать десятки…
Давайте отнимем от 8345 число 978.
Первый пример был очень простым, потому, что все цифры второго числа были меньше чем верхние…
Давайте возьмем другое число и попытаемся отнять столбиком…
Нам потребуется занимать десятки…
Давайте отнимем от 8345 число 978.
Опять выграниваем по правому краю.
Здесь существует правило! Если в одном столбце верхняя цифра меньше нижней, то нужно занимать единицу у следующей слева цифры.
Отнять от 5 8 не получится. Поэтому нужно занять единицу от 4 ставим апостроф над цифрой 4 – это означает, что там уже не 4, а на единицу меньше… 3
Чтобы понять, что это значит, то возьмите число 45 и представьте ё в виде 45 = 30 + 15
30 – это первая цифра(3) этого числа = 4 с апострофом и от 15 вычитаем 8 = 7 – опускаем за черту…
4 с апострофом = 3 от неё надо вычесть 7 – повторятся аналогичная ситуация, что и первом случае…
Вместо 83 у нас 82, можно отнять так же столбиком, а можно и так… в уме 82 – 9 = 73
Опять выграниваем по правому краю.
Здесь существует правило! Если в одном столбце верхняя цифра меньше нижней, то нужно занимать единицу у следующей слева цифры.
Отнять от 5 8 не получится. Поэтому нужно занять единицу от 4 ставим апостроф над цифрой 4 – это означает, что там уже не 4, а на единицу меньше… 3
Чтобы понять, что это значит, то возьмите число 45 и представьте ё в виде 45 = 30 + 15
30 – это первая цифра(3) этого числа = 4 с апострофом и от 15 вычитаем 8 = 7 – опускаем за черту…
4 с апострофом = 3 от неё надо вычесть 7 – повторятся аналогичная ситуация, что и первом случае…
Вместо 83 у нас 82, можно отнять так же столбиком, а можно и так… в уме 82 – 9 = 73
Как объяснить ребёнку вычитание в столбик.
Начнем с объяснения вычитания в столбик однозначных! С чего то надо начинать!
Вычитание в столбик однозначных объяснение для ребенка.
Т.е. показываем ребенку 9 пальцев:
Убираем одну руку, которая обозначает 5 пальцев.
Спрашиваем у ребенка, сколько остается.
Проделываем так несколько раз, на разных числах.
Переходим на вычитание в столбик для ребенка
Если визуально мы добились того, что это не вызывает проблем с подсчетом, переходим к вычитанию однозначных в столбик!
Располагаем число 9 в верхней строчке.
Ниже записываем второе число.
Под ним горизонтальную линию.
Вспоминаем упражнение с пальцами и записываем результат под чертой.
Повторяем аналогичные задачки несколько раз, чтобы вычитание однозначных въелось в подкорку и делалось на автомате!
Как объяснить ребёнку вычитание в столбик двузначных
Теперь стоит задача объяснить ребенку вычитание двузначных.
Начинать нужно, конечно, с вычитания однозначного от двузначного.
Предположим, что нам нужно вычесть от 19 тоже число 5.
Если ребенок еще плохо считает, объясняем ему на пальцах, аналогично, что в этом пунтке
Вы можете задействовать его 10 пальцев и свои 10.(это уже 20.)
Показываем ребенку 19 пальцев.
Спрашиваем сколько получилось у ребенка.
В начале, это будет очень тяжело, но поверьте мне, частое повторение приводит к автоматизму!
После того, как закрепили визуальное вычитание, можно переходить к вычитанию в столбик!
Проделываем те же операции, что в этом пункте.
Записываем аналогично в столбик.
вычитаем от 9 число 5,
единицу мы никак не трогали, поэтому её опускаем за черту нетронутой!
Если вы смогли объяснить этот пример, то можно переходить к вычитанию в столбик, когда нижнее число больше верхнего.
Эти варианты описаны выше в пунктах 1,2,3 вместе с правилом идут примеры.
Вычитание натуральных чисел столбиком: примеры, решения
Существует удобный метод нахождения разности двух натуральных чисел – вычитание в столбик, или вычитание столбиком. Этот способ берет свое название от метода записи уменьшаемого и разности друг под другом. Так можно провести и основные, и промежуточные вычисления в соответствии с нужными разрядами чисел.
Этим методом удобно пользоваться, поскольку это очень просто, быстро и наглядно. Все сложные на первый взгляд подсчеты можно свести к сложению и вычитанию простых чисел.
Ниже мы рассмотрим, как именно пользоваться этим методом. Наши рассуждения будут подкреплены примерами для большей наглядности.
Что нужно повторить перед изучением вычитания столбиком?
Кроме того, важно знать, как определять разряд натуральных чисел.
Разбор метода вычитания столбиком
Главное на первом этапе – правильно записать исходные данные. Для начала записываем первое число, из которого будем вычитать. Под ним располагаем вычитаемое. Цифры должны быть расположены строго одна под другой с учетом разряда: десятки под десятками, сотни под сотнями, единицы под единицами. Запись читается справа налево. Далее ставим минус с левой стороны от столбика и подводим черту под обоими числами. Под ней будет записываться конечный результат.
Покажем на примере, какая запись подсчета является правильной:
Как видно, с помощью этого метода можно производить вычисления разной сложности.
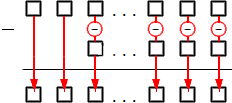
Далее рассмотрим сам процесс нахождения разности. Для этого выполняем поочередное вычитание значений разрядов: сначала вычитаем единицы из единиц, потом десятки из десятков, потом сотни из сотен и т.д. Значения записываем под чертой, отделяющей исходные данные от результата. В итоге у нас должно получиться число, которое и будет верным ответом задачи, т.е. разностью исходных чисел.
Как именно выполняются подсчеты, можно увидеть на этой схеме:
С общей картиной записи и подсчета мы разобрались. Однако в методе есть и некоторые моменты, нуждающиеся в уточнении. Для этого мы приведем конкретные примеры и поясним их. Начнем с простейших задач и будем постепенно наращивать сложность, пока наконец не разберем все нюансы.
Советуем внимательно прочитать все примеры, потому что каждый из них иллюстрирует отдельные непонятные моменты. Если вы дойдете до конца и запомните все объяснения, то подсчет разности натуральных чисел в дальнейшем не будет вызывать у вас ни малейших затруднений.
Решение:
Запишем эти числа одно под другим, правильно расположив разряды друг под другом, и подчеркнем их:
Вычитаем десятки. Оба значения в нашем столбике нулевые, а вычитание нуля из нуля всегда дает нуль (как вы помните, мы упоминали, что нам в дальнейшем потребуется это свойство вычитания). Результат записываем в нужное место:
Нам остается подсчитать только разность между цифрами, означающими десятки тысяч. Пишем последнюю цифру под чертой и смотрим, что у нас вышло:
Возьмем другой пример:
Решение:
Шаги, которые нам нужно сделать, мы уже приводили выше. Выполняем их последовательно для новых чисел и получаем в итоге:
Если посмотреть на условия двух примеров, приведенных выше, легко заметить, что до сих пор мы брали только числа, равные по количеству знаков. Но метод столбика можно использовать и тогда, когда уменьшаемое включает в себя больше знаков, чем вычитаемое.
Решение
Запишем числа друг под другом, соблюдая нужную соотнесенность разрядов. Это будет выглядеть так:
Теперь поочередно вычисляем значения:
Запишем, что у нас получилось:
Вычитаемое имеет значения в месте десятков и сотен тысяч, а вот уменьшаемое нет. Что же делать? Вспомним, что пустота в математических примерах равнозначна нулю. Значит, нам нужно вычесть нули из исходных значений. Вычитание нуля из натурального числа всегда дает нуль, следовательно, все, что нам остается, – это переписать исходные значения разрядов в область ответа:
В наших примерах значения разрядов вычитаемого всегда оказывались меньше, чем значения уменьшаемого, поэтому никаких трудностей при подсчете это не вызывало. Что делать, если из значения верхней строки нельзя вычесть значение нижней, не уйдя при этом в минус? Тогда нам нужно «взять взаймы» значения более старших разрядов. Возьмем конкретный пример.
Получившийся результат пишем на нужном месте под чертой:
Зачастую выполнять действие «размена» в рамках одного примера приходится несколько раз. Разберем такую задачу.
Решение
Возьмем еще более сложный пример.
Решение
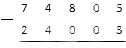
В первом шаге, как и ранее, нам приходится вычитать двойку из семерки. Идем в десятки за «разменом». Но у нас их нет, как нет и сотен: на месте этих разрядов у уменьшаемого стоят нули. Поэтому идем сразу в тысячу. Это 10 сотен, так что:
После этого одну сотню представляем в виде 10 десяток:
Финальное действие в «размене» – один десяток на 10 единиц. Получим:
У нас остался последний шаг. Мы видим оставшееся число восемь с точкой, означающей, что ее надо уменьшить на единицу. Считаем число 8 − 1 = 7 :
Это были все сложные моменты, которые мы хотели пояснить. Они пригодятся для быстрых вычислений на практике. Завершим статью еще одним примером, но без комментариев: