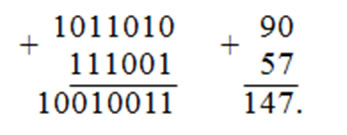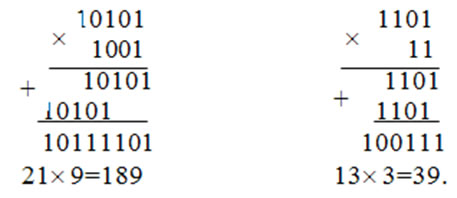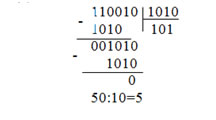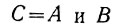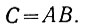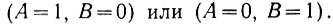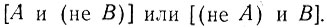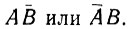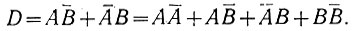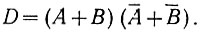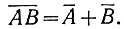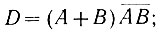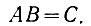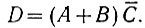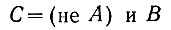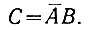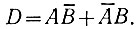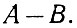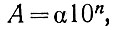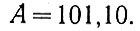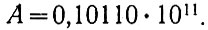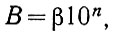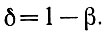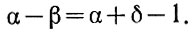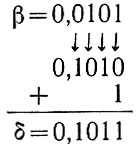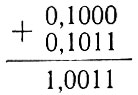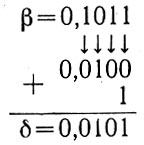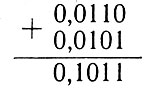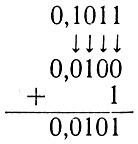Как правильно вычитать двоичные числа

Системы счисления. Арифметические действия в двоичной системе счисления

Цель: научить учащихся выполнять арифметические действиями в двоичной системе счисления.
Задачи:
образовательные:
— повторение и закрепление знаний учащихся о системах счисления;
— формировать у школьников умение выполнять правильно арифметические действия в двоичной системе счисления;
развивающие:
— развивать логическое мышление учащихся;
— развивать познавательный интерес учеников.

Содержание нового материала: правила сложения, умножения, вычитания и деления в двоичной системе счисления.

Ход урока.

Изучение нового материала.
Правила сложения:
0+0=0
0+1=1
1+0=1
1+1=10
Обратить внимание учащихся на то, что при сложении двух единиц в двоичной системе счисления в записи получается 0, а единица переносится в следующий разряд. При сложении трех единиц получается в записи 1, и единица переносится в следующий разряд. (1+1+1=11).

Пример 1.
101+10=111

Пример 2.
10011+11=1110

Учащиеся самостоятельно решают следующие примеры:
1001+11=1100
110+110=1100

Правила умножения:
0*0=0
0*1=0
1*0=0
1*1=1

Пример 1.
101*11=1111

Пример 2.
1011*101=110111

Учащиеся самостоятельно решают следующие примеры:
1001*101=101101
1001*11=11011

Правила вычитания:
0-0=0
1-0=1
1-1=0
0-1=-1
Обратить внимание учащихся на то, что «минус» в последнем правиле обозначает – «занять разряд (1)».

Пример 1.
10110-111=1111

Объяснение:
Вычитание выполняется так же, как в математике. Если цифра в уменьшаемом меньше цифры вычитаемого, то для данного вычитания необходимо занять разряд (1), т.к. 10-1=1. Если слева от такого вычитания стоит 0, то мы не можем занять разряд. В этом случае разряд занимаем в уменьшаемом у близстоящей слева от данного вычитания единицы. При этом все нули, у которых мы не могли занять разряд, необходимо поменять на единицу, т.к. 0-1=-1. Желательно все изменения в цифрах записывать сверху данного вычитания. Дальнейшее вычитание выполнять с получившимися сверху цифрами.

Пример 2.
100000-11=11101

Учащиеся самостоятельно решают следующие примеры:
100010-100=
101011-10111=

Правило деления:
Деление выполняется по правилам математики, не забывая, что мы выполняем действия в двоичной системе счисления.

Пример 1.
101101:1001=101

Источник

Двоичная арифметика

Всего получено оценок: 190.

Всего получено оценок: 190.

Операции сложения, вычитания, умножения и деления в двоичной системе – это двоичная арифметика. Некоторые примеры двоичной арифметики рассмотрены в данной статье.

Двоичная арифметика

Все арифметические действия, которые применимы к двоичным числам, выполняются аналогично как в десятичной системе. Удобнее всего двоичные числа складывать, вычитать, умножать и делить столбиком.

Числа записываются друг под другом с учетом разрядов. При необходимости производится перенос в старший разряд или заем из старшего разряда.

При сложении двоичных чисел следует помнить, что в числовом двоичном ряду после 1 идет 10. Это означает, что 1 + 1 = 10, а 11 + 1= 100.

Изучению двоичной системы много времени посвятил В. Лейбниц. По его просьбе была отчеканена медаль в честь двоичной системы, на которой отображались простейшие арифметические действия с двоичными числами.

Сложение

Вычисление суммы двоичных чисел производится следующим образом: числа записываются в столбик. Затем производится поразрядное суммирование цифр, начиная с младшего разряда, как в десятичной системе. Если сумма цифр текущего разряда превышает его размер, то происходит перенос единицы в старший разряд.

Правила сложения двоичных чисел:

Например, сумма двоичных чисел 1000111 + 110011 = 1111010

Источник

Информатика и информационные технологии: конспект лекций.

Арифметические операции над целыми двоичными числами.

Сложение двоичных чисел без знака.

Микропроцессор выполняет сложение операндов по правилам сложения двоичных чисел. Проблем не возникает до тех пор, пока значение результата не превышает размерности поля операнда. Например, при сложении операндов размером в байт результат не должен превышать число 255. Если это происходит, то результат оказывается неверным. Рассмотрим, почему так происходит.

К примеру, выполним сложение: 254 + 5 = 259 в двоичном виде. 11111110 + 0000101 = 1 00000011. Результат вышел за пределы 8 бит и правильное его значение укладывается в 9 бит, а в 8-битовом поле операнда осталось значение 3, что, конечно, неверно. В микропроцессоре этот исход сложения прогнозируется и предусмотрены специальные средства для фиксирования подобных ситуаций и их обработки. Так, для фиксирования ситуации выхода за разрядную сетку результата, как в данном случае, предназначен флаг переноса сf. Он располагается в бите 0 регистра флагов ЕFLАGS/FLАGS. Именно установкой этого флага фиксируется факт переноса единицы из старшего разряда операнда. Естественно, что программист должен учитывать возможность такого исхода операции сложения и предусматривать средства для корректировки. Это предполагает включение участков кода после операции сложения, в которых анализируется флаг сf. Анализ этого флага можно провести различными способами.

Самый простой и доступный – использовать команду условного перехода jсс. Эта команда в качестве операнда имеет имя метки в текущем сегменте кода. Переход на эту метку осуществляется в случае, если в результате работы предыдущей команды флаг сf установился в 1. В системе команд микропроцессора имеются три команды двоичного сложения:

1) inс операнд – операция инкремента, т. е. увеличения значения операнда на 1;

2) аdd операнд_1, операнд_2 – команда сложения с принципом действия: операнд_1 = операнд_1 + операнд_2;

3) аdс операнд_1, операнд_2 – команда сложения с учетом флага переноса сf. Принцип действия команды: операнд_1 = операнд_1 + операнд_2 + значение_сГ.

Обратите внимание на последнюю команду – это команда сложения, учитывающая перенос единицы из старшего разряда. Механизм появления такой единицы мы уже рассмотрели. Таким образом, команда аdс является средством микропроцессора для сложения длинных двоичных чисел, размерность которых превосходит поддерживаемые микропроцессором длины стандартных полей.

Сложение двоичных чисел со знаком.

На самом деле микропроцессор «не подозревает» о различии между числами со знаком и без знака. Вместо этого у него есть средства фиксирования возникновения характерных ситуаций, складывающихся в процессе вычислений. Некоторые из них мы рассмотрели при обсуждении сложения чисел без знака:

1) флаг переноса сf, установка которого в 1 говорит о том, что произошел выход за пределы разрядности операндов;

2) команду аdс, которая учитывает возможность такого выхода (перенос из младшего разряда).

Другое средство – это регистрация состояния старшего (знакового) разряда операнда, которое осуществляется с помощью флага переполнения оf в регистре ЕFLАGS (бит 11).

Вы, конечно, помните, как представляются числа в компьютере: положительные – в двоичном коде, отрицательные – в дополнительном коде. Рассмотрим различные варианты сложения чисел. Примеры призваны показать поведение двух старших битов операндов и правильность результата операции сложения.

00687 = 00000010 10101111.

31253 = 01111010 00010101.

Следим за переносами из 14 и 15-го разрядов и правильностью результата: переносов нет, результат правильный.

1132 = 11101110 11001100.

Произошел перенос из 14-го разряда; из 15-го разряда переноса нет. Результат неправильный, так как имеется переполнение – значение числа получилось больше, чем то, которое может иметь 16-битное число со знаком (+32 767).

-30566 = 10001000 10011010.

-04875 = 11101100 11110101.

-35441 = 01110101 10001111.

Произошел перенос из 15-го разряда, из 14-го разряда нет переноса. Результат неправильный, так как вместо отрицательного числа получилось положительное (в старшем бите находится 0).

-4875 = 11101100 11110101.

-4875 = 11101100 11110101.

09750 = 11011001 11101010.

Есть переносы из 14 и 15-го разрядов. Результат правильный.

Таким образом, мы исследовали все случаи и выяснили, что ситуация переполнения (установка флага ОF в 1) происходит при переносе:

1) из 14-го разряда (для положительных чисел со знаком);

2) из 15-го разряда (для отрицательных чисел).

И наоборот, переполнения не происходит (т. е. флаг ОF сбрасывается в 0), если есть перенос из обоих разрядов или перенос отсутствует в обоих разрядах.

Итак, переполнение регистрируется с помощью флага переполнения оf. Дополнительно к флагу оf при переносе из старшего разряда устанавливается в 1 и флаг переноса СF Так как микропроцессор не знает о существовании чисел со знаком и без знака, то вся ответственность за правильность действий с получившимися числами ложится на программиста. Проанализировать флаги СF и ОF можно командами условного перехода JС\JNС и JО\JNО соответственно.

Что же касается команд сложения чисел со знаком, то они те же, что и для чисел без знака.

Вычитание двоичных чисел без знака.

Как и при анализе операции сложения, порассуждаем над сутью процессов, происходящих при выполнении операции вычитания. Если уменьшаемое больше вычитаемого, то проблем нет, – разность положительна, результат верен. Если уменьшаемое меньше вычитаемого, возникает проблема: результат меньше 0, а это уже число со знаком. В этом случае результат необходимо завернуть. Что это означает? При обычном вычитании (в столбик) делают заем 1 из старшего разряда. Микропроцессор поступает аналогично, т. е. занимает 1 из разряда, следующего за старшим, в разрядной сетке операнда. Поясним на примере.

05 = 00000000 00000101.

-10 = 00000000 00001010.

Для того чтобы произвести вычитание, произведем.

Воображаемый заем из старшего разряда:

Тем самым, по сути, выполняется действие.

(65 536 + 5) – 10 = 65 531.

5 = 00000000 00000101.

(-10)= 11111111 11110110.

Т. е. мы получили тот же результат, что и в предыдущем примере.

Таким образом, после команды вычитания чисел без знака нужно анализировать состояние флага СЕ Если он установлен в 1, то это говорит о том, что произошел заем из старшего разряда и результат получился в дополнительном коде.

Аналогично командам сложения группа команд вычитания состоит из минимально возможного набора. Эти команды выполняют вычитание по алгоритмам, которые мы сейчас рассматриваем, а учет особых ситуаций должен производиться самим программистом. К командам вычитания относятся следующие:

1) dес операнд – операция декремента, т. е. уменьшения значения операнда на 1;

2) sub операнд_1, операнд_2 – команда вычитания; ее принцип действия: операнд_1 = операнд_1 – операнд_2;

3) sbb операнд_1, операнд_2 – команда вычитания с учетом заема (флага сi): операнд_1 = операнд_1 – операнд_2 – значение_сГ.

Как видите, среди команд вычитания есть команда sbb, учитывающая флаг переноса сf. Эта команда подобна аdс, но теперь уже флаг сf исполняет роль индикатора заема 1 из старшего разряда при вычитании чисел.

Вычитание двоичных чисел со знаком.

Здесь все несколько сложнее. Микропроцессору незачем иметь два устройства – сложения и вычитания. Достаточно наличия только одного – устройства сложения. Но для вычитания способом сложения чисел со знаком в дополнительном коде необходимо представлять оба операнда – и уменьшаемое, и вычитаемое. Результат тоже нужно рассматривать как значение в дополнительном коде. Но здесь возникают сложности. Прежде всего они связаны с тем, что старший бит операнда рассматривается как знаковый. Рассмотрим пример вычитания 45 – (-127).

Вычитание чисел со знаком 1.

Судя по знаковому разряду, результат получился отрицательный, что, в свою очередь, говорит о том, что число нужно рассматривать как дополнение, равное —44. Правильный результат должен быть равен 172. Здесь мы, как и в случае знакового сложения, встретились с переполнением мантиссы, когда значащий разряд числа изменил знаковый разряд операнда. Отследить такую ситуацию можно по содержимому флага переполнения оf. Его установка в 1 говорит о том, что результат вышел за диапазон представления знаковых чисел (т. е. изменился старший бит) для операнда данного размера, и программист должен предусмотреть действия по корректировке результата.

Вычитание чисел со знаком 2.

Здесь все нормально, флаг переполнения оf сброшен в 0, а 1 в знаковом разряде говорит о том, что значение результата – число в дополнительном коде.

Вычитание и сложение операндов большой размерности.

Если вы заметили, команды сложения и вычитания работают с операндами фиксированной размерности: 8, 16, 32 бит. А что делать, если нужно сложить числа большей размерности, например 48 бит, используя 16-разрядные операнды? К примеру, сложим два 48-разрядных числа:

Рис. 29. Сложение операндов большой размерности.

На рисунке 29 по шагам показана технология сложения длинных чисел. Видно, что процесс сложения многобайтных чисел происходит так же, как и при сложении двух чисел «в столбик», – с осуществлением при необходимости переноса 1 в старший разряд. Если нам удастся запрограммировать этот процесс, то мы значительно расширим диапазон двоичных чисел, над которыми мы сможем выполнять операции сложения и вычитания.

Принцип вычитания чисел с диапазоном представления, превышающим стандартные разрядные сетки операндов, тот же, что и при сложении, т. е. используется флаг переноса сf. Нужно только представлять себе процесс вычитания в столбик и правильно комбинировать команды микропроцессора с командой sbb.

В завершение обсуждения команд сложения и вычитания отметим, что кроме флагов сf и оf в регистре еflаgs есть еще несколько флагов, которые можно использовать с двоичными арифметическими командами. Речь идет о следующих флагах:

1) zf – флаг нуля, который устанавливается в 1, если результат операции равен 0, и в 1, если результат не равен 0;

2) sf – флаг знака, значение которого после арифметических операций (и не только) совпадает со значением старшего бита результата, т. е. с битом 7, 15 или 31. Таким образом, этот флаг можно использовать для операций над числами со знаком.

Умножение чисел без знака.

Для умножения чисел без знака предназначена команда.

Как видите, в команде указан всего лишь один операнд-сомножитель. Второй операнд-сомножитель_2 задан неявно. Его местоположение фиксировано и зависит от размера сомножителей. Так как в общем случае результат умножения больше, чем любой из его сомножителей, то его размер и местоположение должны быть тоже определены однозначно. Варианты размеров сомножителей и размещения второго операнда и результата приведены в таблице 10.

Источник

Арифметические операции в двоичной системе

Арифметические действия в двоичной системе производится по тем же правилам что и в десятичной системе счисления. Однако так как в двоичной системе счисления используются только две цифры 0 и 1, то арифметические действия выполняются проще, чем десятичной системе.

Сложение двоичных чисел.

Сложение выполняется поразрядно столбиком, начиная с младшего разряда и используя таблицы двоичного сложения:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10.

При сложении необходимо помнить, что 1+1 дают нуль в данном разряде и единицу переноса в старший.

Пример 3.5. Сложить два числа:

Вычитание двоичных чисел.

Вычитание выполняется поразрядно столбиком, начиная с младшего разряда и используя таблицы двоичного вычитания:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1.
Пример 3.6. Найти разность двух чисел:

Т.е. при вычитании двоичных чисел в случае необходимости занимается 1 из старшего разряда, которая равна двум единицам младшего разряда.

Умножение двоичных чисел.

Как видно из приведенных примеров, операция умножения может быть представлена как операции сдвига и суммирования.

Деление двоичных чисел.

Деление в двоичной системе производится вычитанием делителя со сдвигом вправо, если остаток больше нуля.
Пример 3.8. Найти частное двух чисел если:
1. Делимое больше делителя:

2. Делимое меньше делителя:

Как видно из приведенных примеров, операция деления может быть представлена как операции сравнения, сдвига и суммирования.

Вернуться в оглавление:Алгоритмические языки

Источник

Как правильно вычитать двоичные числа

2. Арифметические действия в двоичной системе

Основываясь на правилах логического умножения и сложения, можно при помощи рассмотренных выше логических электронных элементов создать устройства, выполняющие операции сложения, вычитания, умножения и деления.

а) Сложение двоичных чисел

Сложение двоичных чисел осуществляется по правилам логического сложения (ур. 2.3). Однако при этом необходимо иметь в виду, что единица, получающаяся при сложении двух единиц, переносится (прибавляется) в более высокий разряд. Поэтому для сложения двух одноразрядных чисел получаем следующие правила:

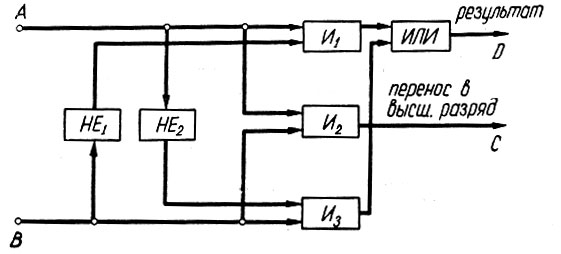
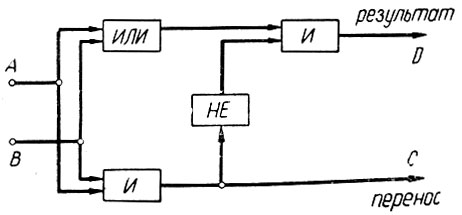
Эти правила могут быть реализованы в схеме, показанной на рис. 2.9, которая составляется следующим образом.

Рис. 2.9. Схема сложения двух чисел

Прежде всего, сигнал переноса (С), как это следует из четвертого равенства (ур. 2.7), имеет место тогда, когда оба слагаемых (А и В) равны единице. Это логическое высказывание можно записать в виде

Поэтому сигнал переноса является выходом логического элемента «И₂«, на входы которого поданы сигналы А и В (рис. 2.9).

Единица в том же разряде получается (ур. 2.7) в двух случаях, когда

Используя терминологию алгебры логики, эти условия можно записать в следующем виде:

Введение условных обозначений логических операций упрощает данную запись:

Это сложное логическое выражение в конечном виде можно записать следующим образом:

Рассматриваемое логическое преобразование может быть выполнено (рис. 2.9) при помощи пяти логических элементов: «HE₁«, «HE₂«, «И₁«, «И₃» и «ИЛИ».

Однако для нахождения результата сложения (D) уравнение (2.8) не является оптимальным (в отношении количества используемых логических элементов). Это происходит потому, что в нем не используется уже имеющийся сигнал переноса С = АВ. Проведенные в этом отношении исследования показывают следующее.

Учитывая, что АА‾ = 0 и ВВ‾ = 0 (ур. 2.6), запишем уравнение (2.8) в следующем виде:

После несложных преобразований получаем:

Как следует из второго уравнения (2.4),

Таким образом, в окончательном виде

Данное логическое высказывание проще, чем высказывание (ур. 2.8). Поэтому сложение выполняется (рис. 2.10) при помощи четырех (а не шести, как в предыдущем случае) логических элементов.

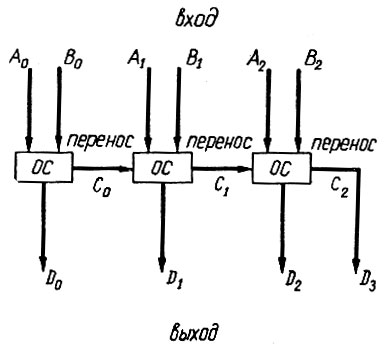
Схемы рис. 2.9 или 2.10 используются лишь при сложении одноразрядных чисел. Для того чтобы сложить два R-разрядных числа, необходимо иметь сумматор, состоящий из одноразрядных сумматоров (ОС). Схема такого сумматора на три разряда показана на рис. 2.11.

Рис. 2.10. Упрощенная схема сложения

Рис. 2.11. Сумматор на три разряда

На вход этого устройства подаются два трехразрядных числа (A₂A₁A₀ и B₂B₁B₀). На выходе получается четырехразрядное число (D₃D₂D₁D₀).

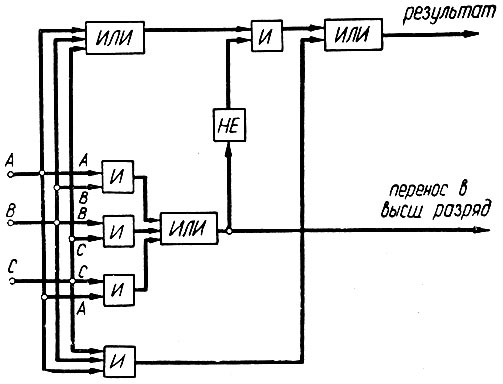
Как следует из этой схемы, каждый одноразрядный сумматор (ОС) должен быть выполнен таким образом, чтобы он мог складывать три одноразрядных числа: А, В и перенос с низшего разряда (С). Одна из схем такого сумматора, выполненная на логических элементах типа «НЕ», «ИЛИ», «И», показана на рис. 2.12.

Рис. 2.12. Сумматор на три одноразрядных числа

б) Вычитание двоичных чисел

Вычитание двоичных чисел может быть выполнено двумя методами.

Прежде всего можно сконструировать устройство, которое, вычитая меньшее число из большего, в каждом разряде выполняет непосредственно вычитание по правилам:

где единица в скобках обозначает перенос (добавление) в высший разряд вычитаемого числа.

Пользуясь этими правилами, легко построить логическую схему, выполняющую вычитание двух одноразрядных чисел.

Это логическое высказывание выполняется (рис. 2.13) при помощи двух логических элементов (НЕ₂ и И₂).

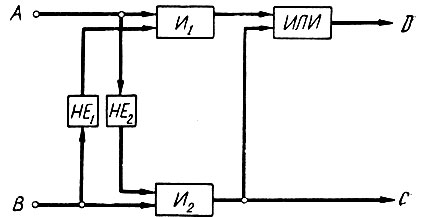
Рис. 2.13. Логическая схема вычитания двух одноразрядных чисел

В результате вычитания единица в том же разряде получается в случае, когда А = 1 и В = 0 или А = 0 и В = 1. Это логическое высказывание, как было показано при рассмотрении операций логического сложения, записывается в следующем виде:

Данное высказывание (рис. 2.13) выполняется пятью логическими элементами, два из которых одновременно используются для получения сигнала переноса (С).

Сравнивая схемы сложения (рис. 2.9) и вычитания (рис. 2.13) одноразрядных чисел, легко увидеть, что они отличаются друг от друга только логикой определения сигнала переноса.

Часто бывает очень удобным на одной и той же схеме выполнять как сложение, так и вычитание. В этом случае операция вычитания специальным приемом сводится к сложению. Делается это следующим образом.

Рассмотрим вычитание двух R-разрядных чисел:

Нормализуем большее из этих двух чисел, т. е. запишем его в следующем виде:

Пример нормализации двоичного числа:

Записывая это число в таком виде, чтобы целая часть отсутствовала и после запятой была единица, получаем:

Запишем теперь меньшее из рассматриваемых чисел (В) в следующем виде:

где n равно показателю нормализованного числа А.

Тогда получим следующее равенство:

Введем далее новое число (δ), которое равно

Из этого равенства следует, что

т. е. δ дополняет β до единицы. Поэтому δ называется дополнительным числом числа β.

Подставив значение β (ур. 2.11) в уравнение (2.10), получаем

Сравнивая уравнения (2.10) и (2.12), можно записать:

Таким образом, для того чтобы вычесть два числа, необходимо к уменьшаемому прибавить число, дополнительное к вычитаемому, и от полученного результата вычесть единицу. Благодаря этому вычитание двух чисел сводится к операции сложения.

Рассмотрим примеры вычитания двух чисел при помощи логических операций сложения (ур. 2.7).

Пример 1. А = 1000 (восемь), В = 101 (пять).

1. Нормализуем большее число:

2. Выравнивая порядок чисел А и В (n = 100), получаем:

3. Находим число, дополнительное к β:

Пример 2. А = 110 (шесть), В = 1011 (одиннадцать).

1. Нормализуем большее число:

2. Выравнивая порядок (n = 100) чисел А и В, получаем:

3. Находим число, дополнительное к β:

5. Вычитаем единицу:

Поскольку в результате вычитания получается отрицательное число, запишем его в следующем виде:

Как было показано выше, вычитание двух чисел, расположенных в круглой скобке, можно свести к операции сложения. Для этого необходимо к уменьшаемому (единице) прибавить число, дополнительное к вычитаемому (0,1011), и из полученного результата вычесть единицу.

6. Определяем число, дополнительное к 0,1011:

в) Умножение двоичных чисел

Умножение одноразрядных чисел выполняется в соответствии с правилами логического умножения (ур. 2.2). Как следует из этих правил, умножение одноразрядных чисел выполняется при помощи логического элемента «И».

Умножение R-разрядных чисел производится так же, как и в элементарной алгебре, и сводится к операциям сложения и сдвига.

Пример. Перемножить числа 101 (пять) и 1011 (одиннадцать).

Умножение выполняется следующим образом:

г) Деление двоичных чисел

Поскольку двоичные одноразрядные числа имеют только два значения (0 и 1), то правила их деления чрезвычайно просты:

Деление R-разрядных чисел выполняется так же, как и в элементарной алгебре, и сводится к операциям вычитания.

Пример. Разделить 110111 (пятьдесят пять) на 101 (пять).

Источник