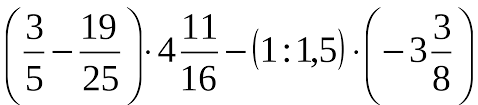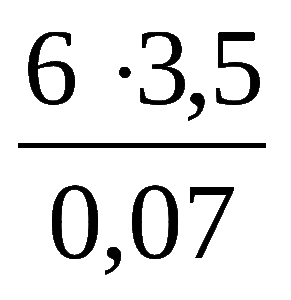Как появилась дроби в математике

История возникновения и развития обыкновенных и десятичных дробей

Дробь — это число, которое состоит из одной или нескольких долей единицы. Они делятся на два типа:

Мы складываем, вычитаем, умножаем и делим дроби, но не задумываемся о том, как они появились. Между тем, история их возникновения, ровно как и рождения любой составляющей современной арифметики, интересна и самобытна.

История возникновения обыкновенных дробей

Как и почему наши предки создали дроби? Причин две: одна практичная, другая — более возвышенная.

Со временем у людей начала появляться потребность в более точных вычислениях. Привычные всем элементарные цифры дробили на несколько частей, и самой мелкой единице меры давали собственное название. Так появились такие определения, как половина, треть, четверть, и так далее.

Древний Египет известен своими невероятными открытиями в области математики. Известен математический папирус Ринда — древнеегипетское учебное руководство по арифметике, в котором и были впервые упомянуты египетские дроби. Для обозначения обыкновенной дроби древние египтяне использовали символ “рот” (вытянутый овал). Некоторые значения (например, 1 2 ) обозначались немного иначе — своеобразными символами. В первую очередь дроби были необходимы для сложных расчетов при строительстве храмов и пирамид. Как мы убеждаемся сейчас, эти расчеты были настолько точными, что большинство творений архитектуры того времени радуют туристов и по сей день.

Разумеется, на этом история появления дробей в математике не закончилась. Из Древнего Египта арифметические символы распространились в Древнюю Грецию, а позже — по всему миру. Некоторые математики, в числе которых был и александрийский ученый Клавдий Птолемей, сомневались в удобстве и правильности египетской системы.

Встречаются развитые системы и в Индии — в частности, в трудах математика Брахмагупты. Обыкновенные дроби записывались им так же, как и сейчас, за единственным исключением — горизонтальная или диагональная черточка отсутствовала, и цифры “висели” в воздухе.

Как появились десятичные дроби

А какова история появления десятичных дробей? Первое упоминание о них относят к третьему веку нашей эры — они появляются в “Математическом трактате” Сунь-Цзы.

Десятичные дроби стали спасением при громоздких вычислениях. Поэтому неудивительно, что наибольшее распространение и “вторую жизнь” они получили в девятнадцатом веке — во время расцвета промышленности, торговли, науки и техники.

Дроби на Руси

Практическое применение дробям нашли в вычислении налогов в пятнадцатом, шестнадцатом и семнадцатом веках. А вот термин “дробь” появился на столетие позже. Как несложно догадаться, слово произошло от глагола “дробить”, “делить на части”.

В шестнадцатом веке в России, как и во всем мире, начала распространяться десятичная система.

Многие школьники и учителя признают, что учение о дробях — одно из самых комплексных и сложных в арифметике. А появилась эта система исчисления благодаря бытовым практическим задачам — в древнем мире долями распределялись не высоколобые ученые, а обычные труженики, которые делили между собой деньги, еду и вещи. Но человек — удивительное существо, способное усложнить и усовершенствовать любую, даже самую примитивную систему. За что мы сейчас и благодарим ученых и математиков прошлого.

Источник

Как появилась дроби в математике

Из истории возникновения обыкновенных дробей.

Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.

Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.

Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.

В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.

Дроби в Древнем Египте

В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.

Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад имели десятичную (но не позиционную) систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.

Дроби в Древней Греции

Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков (к примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой). Максим Плануд греческий монах, ученый, математик в 13 веке ввел название числителя и знаменателя

В Греции употреблялись наряду с единичными, «египетскими» дробями и общие обыкновенные дроби. Среди разных записей употреблялась и такая: сверху знаменатель, под ним – числитель дроби. Например, означало три пятых. Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями.

Дроби в Индии.

Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Зато вся дробь помещалась в прямоугольную рамку. Иногда использовалось и «трехэтажное» выражение с тремя числами в одной рамке; в зависимости от контекста это могло обозначать неправильную дробь (a + b/c) или деление целого числа a на дробь b/c. Правила действий над дробями почти не отличались от современных.

Дроби у арабов.

Записывать дроби как сейчас стали арабы. Средневековые арабы пользовались тремя системами записи дробей. Во-первых, на индийский манер записывая знаменатель под числителем; дробная черта появилась в конце XII – начале XIII в. Во-вторых, чиновники, землемеры, торговцы пользовались исчислением аликвотных дробей, похожим на египетское, при этом применялись дроби со знаменателями, не превышающими 10 (только для таких дробей арабский язык имеет специальные термины); часто использовались приближенные значения; арабские ученые работали над усовершенствованием этого исчисления. В-третьих, арабские ученые унаследовали вавилонско-греческую шестидесятеричную систему, в которой, как и греки, применяли алфавитную запись, распространив ее и на целые части.

Дроби в Вавилоне

Вавилоняне пользовались всего двумя цифрами. Вертикальная черточка обозначала одну единицу, а угол из двух лежащих черточек – десять. Эти черточки у них получались в виде клиньев, потому что вавилоняне писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали.

В древнем Вавилоне предпочитали постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы счисления. Скорее всего здесь учитывалось основание 60, которое кратно 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты.

Но было неудобно работать над натуральными числами, записанными по десятичной системе, и дробями, записанными по шестидесятеричной. А работать с обыкновенными дробями было уже совсем трудно. Поэтому голландский математик Симон Стевин предложил перейти к десятичным дробям.

Дроби в Древнем Китае

В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.

Дроби в Древнем Риме

Дроби на Руси

В русском языке слово «дробь» появилось лишь в VIII веке. Происходит слово «дробь» от слова «дробить, разбивать, ломать на части». У других народов название дроби также связано с глаголами «ломать», «разбивать», «раздроблять». В первых учебниках дроби назывались «ломанные числа». В старых руководствах находили следующие названия дробей на Руси:

– половина, полтина, – треть,

– полполчеть, – полполполтреть (малая треть),

– полполполчеть (малая четь), – пятина,

Древние математики 100/11 не считали дробью. Остаток от деления 1 фунт предлагается поменять на яйца, которых можно было купить 91 штуки. Если 91:11 то получится по 8 яиц и 3 яйца в остатке. Автор рекомендует отдать их тому, кто делил, или же поменять на соль, чтобы посолить яйца.

Десятичные дроби.

Уже несколько тысячелетий человечество пользуется дробными числами, а вот записывать их удобными десятичными знаками оно додумалось значительно позже.

Почему же люди перешли от обыкновенных дробей к десятичным? Да потому, что действия с ними более простые, особенно сложение и вычитание.

Появились десятичные дроби в трудах арабских математиков в Средние века и независимо от них в древнем Китае. Но и раньше, в древнем Вавилоне, использовали дроби такого же типа, только шестидесятеричные.

Позднее учёный Гартман Бейер (1563-1625) выпустил сочинение “Десятичная логистика”, где писал: “…я обратил внимание на то, что техники и ремесленники, когда измеряют какую-нибудь длину, то очень редко и лишь в исключительных случаях выражают её в целых числах одного наименования; обыкновенно им приходится или брать мелкие меры, или обращаться к дробям. Точно так же астрономы измеряют величины не только в градусах, но и в долях градуса, т.е. минутах, секундах и т.п. Их деление на 60 частей не так удобно, как деление на 10, на 100 частей и т.д., потому что в последнем случае гораздо легче складывать, вычитать и вообще производить арифметические действия; мне кажется, что десятичные доли, если бы ввести вместо шестидесятеричных, пригодились бы не только для астрономии, но и для всякого рода вычислений”.

Сегодня мы пользуемся десятичными дробями естественно и свободно. Однако то, что кажется естественным нам, служило настоящим камнем преткновения для учёных Средневековья. В Западной Европе 16 в. вместе с широко распространённой десятичной системой представления целых чисел в расчётах повсюду применялись шестидесятеричные дроби, восходящие ещё к древней традиции вавилонян. Понадобился светлый ум нидерландского математика Симона Стевина, чтобы привести запись и целых, и дробных чисел в единую систему. По-видимому, толчком создания десятичных дробей послужили составленные им таблицы сложных процентов. В 1585 г. он опубликовал книгу “Десятина”, в которой объяснил десятичные дроби.

С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. В Англии в качестве знака, отделяющего целую часть от дробной, была введена точка. Запятая, как и точка, в качестве разделительного знака была предложена в 1617 году математиком Непером.

Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в нашей стране в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.

Дроби в музыке.

Пифагорейцы, много занимавшихся музыкой и обожествлявшие число, считали, что Земля имеет форму шара и находится в центре Вселенной: ведь нет никаких оснований, чтобы она была смещена или вытянута в какую-то одну сторону. Солнце же, Луна и 5 планет (Меркурий, Венера, Марс, Юпитер и Сатурн) движутся вокруг Земли. Расстояния от них до нашей планеты таковы, что они как бы составляют семиструнную арфу, и при их движении возникает прекрасная музыка – музыка сфер. Обычно люди не слышат её из-за суеты жизни, и лишь после смерти некоторые из них смогут насладиться ею. А Пифагор слышал её при жизни.

Его ученики – пифагорейцы, много занимавшиеся музыкой и обожествлявшие число, исследовали, насколько повышается тон струны, если её прижать посередине, или на четверть расстояния одного из концов, или на треть. Обнаружилось, что одновременное звучание двух струн приятно для слуха, если длины их относятся как 1:2, или 2:3, или 3:4, что соответствует музыкальным интервалам в октаву, квинту и кварту. Гармония оказалась тесно связанной с дробями, что подтверждало основную мысль пифагорейцев: «число правит миром»…

Так дроби сыграли определяющую роль в музыке. И сейчас в общепринятой нотой записи длинная нота – целая – делится на половинки (вдвое короче), четверти, восьмые, шестнадцатые и тридцать вторые.

Я учусь в музыкальной школе, и я знаю, что 6/8 – это три четверти, и что в одной половине восемь шестнадцатых. Разучивая новую пьесу, я вслух отсчитываю каждую ноту в такте («раз и, два и…») даже и не подозревая, что считает обыкновенные дроби. Таким образом, ритмический рисунок любого музыкального произведения, созданного европейской культурой, каким бы сложным он ни был, определяется двоичными дробями.

В процессе познания действительности математика играет все возрастающую роль. Сегодня нет такой области знаний, где в той или иной степени не использовались бы математические понятия и методы. Проблемы, решение которых раньше считалось невозможным, успешно решаются благодаря применению математики, тем самым расширяются возможности научного познания. Математика всегда была неотъемлемой и существеннейшей составной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и важной компонентой развития личности.

Литература

М.Я.Выгодский «Арифметика и алгебра в Древнем мире».

Источник

Ученический проект «История возникновения обыкновенных дробей»

Описание презентации по отдельным слайдам:

История возникновения обыкновенных дробей Проект выполнили обучающиеся 6 класса филиала Сосновской СОШ №1 в д.Семикино Гачаева Сабина, Синельникова Дарья, Левин Андрей Руководитель: учитель математики Караваева Н.И

Цель: Выяснить, как возникли обыкновенные дроби

Задачи Изучить историю возникновения обыкновенных дробей Убедиться в важности изучения обыкновенных дробей

Самой древней математической деятельностью был счет. Счет был необходим для того, чтобы следить за поголовьем скота и вести торговлю с другими племенами. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела. Как правило это были пальцы рук и ног.

Первое понятие дроби появилось в связи с необходимостью дележа добычи после охоты, с потребностью измерять длину, площадь, объем, время и другие величины. При этом результат дележа добычи или измерений не всегда удавалось выразить натуральным числом. Приходилось учитывать и части употребляемой меры

Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3, 4 и более частей. Таким образом, в связи с необходимой работой люди стали употреблять выражения: половина, треть, четверть и т.д. Это позволяет сделать вывод, что дробные числа возникли как результат измерения величин.

Дроби в Древнем Египте В древнем Египте пользовались только простейшими дробями, у которых числитель равен единице (те, которые мы называем «долями»). Математики называют такие дроби аликвотными (от лат. aliquot – несколько). Так же используется название основные дроби или единичные дроби. Египтяне использовали только две дроби не являющиеся долями – две трети и три четверти. Эти дроби часто встречались в вычислениях. Для них существовали специальные символы, был специальный знак и для дроби 1/2.

Таблица обозначений иероглифов дробей Иероглиф Значение Примерная величина большая часть глаза 1/2 (или 32/64) зрачок 1/4 (или 16/64) бровь 1/8 (или 8/64) меньшая часть глаза 1/16 (или 4/64) капля слезы 1/32 (или ²/64) знак сокола 1/64 Уаджет 63/64

Дроби в Древнем Риме Римляне пользовались, в основном, только конкретными дробями, которые заменяли абстрактные части подразделами используемых мер. Эта система дробей основывалась на делении на 12 долей единицы веса, которая называлась асс. Так возникли римские двенадцатеричные дроби, т.е. дроби у которых знаменатель всегда был двенадцать. Двенадцатую долю асса называли унцией. Вместо 1\12 римляне говорили «одна унция», 5\12 – «пять унций» и т.д.

. Интересно отметить, что хотя в славянской нумерации запись числа шла слева направо, от высших единиц к низшим, но для чисел от 11 до 19 делалось исключение: сначала писали единицы, а затем знак для 10.

Учение о дробях считалось самым трудным разделом математики во все времена и у всех народов. Кто знал дроби, был в почете. Автор старинной славянской рукописи XVв. пишет: «Несть се дивно, что …в целых, но есть похвально, что в долях…».

В нашей работе мы показали, что дроби появились очень давно и на протяжения всего времени своего существования, человек использовал на ряду с целыми числами дроби. Мы узнали, что дроби появились для более точного счёта; слово дробь произошло от слова «дробить», «ломать», «разбивать на части»; дробная черта появилась всего 300 лет назад; в каждой культуре были и есть интересные задачи с дробями; дроби были важны для решения практических задач. И раз древние египтяне, вавилоняне, римляне и др. могли использовать дроби и проводить вычисления с использованием дробей, то и современный человек, даже имея современную вычислительную технику, обязан уметь пользоваться дробями.

Источники: http://petrovalydmila1.ucoz.ru/load/istorija_vozniknovenija_drobej/1-1-0-7 http://nsportal.ru/ap/library/drugoe/2012/01/16/istoriya-vozniknoveniya-obyknovennykh-drobey Глейзер Г. И. История математики в школе: IV-VI кл. Пособие для учителей. – М.: Просвещение, 1981. Энциклопедия для детей. Том 11. Математика. Москва, «Аванта+»,1998. http://ru.wikipedia.org/wiki.Материал из Википедии — свободной энциклопедии.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-291655

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

При детском омбудсмене в России создадут платформу для взаимодействия с родителями

Время чтения: 2 минуты

В Липецкой области начинающие педагоги получат 120 тысяч рублей

Время чтения: 0 минут

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Рособрнадзор разрешил провести ВПР по некоторым предметам на компьютерах

Время чтения: 0 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Исследовательская работа по математике «История возникновения дробей» (5 класс)

Муниципальное бюджетное общеобразовательное учреждение «Карапсельская средняя общеобразовательная школа №13»

«История возникновения дробей»

Найденова Нина Ивановна

1. История возникновения обыкновенных дробей………………… 5

1.1 Возникновение дробей……………………………………………

1.2 Дроби в Древнем Вавилоне………………………………………

1.3 Дроби в Древнем Риме……………………………………………

1.4 Дроби в Древнем Египте…………………………………………

1.5 Дроби Древней Греции………………………………………….

1.7 Дроби в других государствах древних и средних веков………..

2. Практическое применение дробей………………………………… 11

2.1 Решение нестандартных задач……………………………………. 11

2.2 Исследование «Из глубины веков»……………………………….. 11

Список источников информации……………………………………… 13

Математика – наука, в которой изучаются геометрические фигуры и числа. На уроках математики в начальной школе изучают не только натуральные числа, но и приступают к рассмотрению долей. В 5 классе на уроках более подробно познакомились с обыкновенными дробями, которые оказались необычными числами. Необходимость в дробных числах возникла в результате практической деятельности человека. Во-первых, потребность в нахождении долей единицы появилась у наших предков при дележе добычи после охоты. Во-вторых, существенной причиной появления дробных чисел следует считать измерение длин, площадей, углов и других величин при помощи выбранной единицы измерения. Для получения более точных результатов меры стали делить на части, что привело к появлению дробей. Актуальность исследования: не всегда в жизни можно обойтись натуральными значениями. С применением дробных значений человек встречается ежедневно, например, при товарно-денежных отношениях, а также очень важно соблюдать дозы применения лекарственных препаратов и так далее.

Таким образом, дроби играют важную роль в жизни человеческого общества. Но на уроках математики при изучении темы «Дроби» мало уделено внимания из истории развития дробей. И мне стало интересно узнать, когда и где впервые появились дроби, как их называли и обозначали, а также их практическое применение.

Объект исследования: дроби.

Предмет исследования: история возникновения дробей.

Гипотеза: я предполагаю, что дроби пригодятся мне в жизни.

Цель исследования: формирование представления возникновения дробей.

1) определить происхождение слова «дробь»;

2) обобщить исторический материал: когда и где впервые упоминается о дробях;

3) рассмотреть исторические задачи с дробями;

4) провести опрос учащихся с целью повышения заинтересованности учащихся при изучении дробей;

5) кратко оформить собранный материал в буклет и распространить его среди учащихся 5-6-х классов;

6) создать электронную презентацию по рассмотренному материалу.

Методы исследования: изучение справочной и математической литературы, анализ информационных материалов, метод сопоставления, аналитический метод.

На защиту выносится презентация работы.

Практическая значимость: собрать и изучить материал по истории создания дробей, расширить знания о видах дробей и первоначальное их применение. Собранный материал оформить в виде буклета и распространить среди ребят (Приложение 2). Созданную электронную презентацию использовать на уроке при изучении дробей.

1. История возникновения обыкновенных дробей

1.1 Возникновение дробей

Было время, когда для счета предметов употреблялись лишь два числительных: один и два. В процессе дальнейшего расширения чисел привлекались части человеческого тела и в первую очередь пальцы, а если не хватало такого рода «цифр», то еще палочки, камешки и другие вещи. Однако при дележе добычи, между охотниками возникали споры, которые привели первобытного человека к делению целого на равные части, то есть к понятию о дробном числе. Кроме того, в жизни человеку приходилось не только считать предметы, но и измерять величины, например, длины, площади земельных участков, объемы, массы тел. При этом случалось, что единица измерения не всегда укладывалась целое число раз в измеряемой величине. И тогда люди делили целое на более мелкие, но равные части. Первой дробью, с которой познакомились люди, была половина. Следующей дробью была треть. В древности у разных народов использовались разные дроби и разные записи дробей.

1.2 Дроби в Древнем Вавилоне

Вавилоняне пользовались всего двумя цифрами. Вертикальная черточка обозначала одну единицу, а угол из двух лежащих черточек – десять. Эти черточки у них получались в виде клиньев, потому что вавилоняне писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали.

В древнем Вавилоне предпочитали постоянный знаменатель, равный шестидесяти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы счисления. Основание 60 возможно учитывалось потому что, оно кратно 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты.

Другие ученые этот факт связывают с тем, что вавилонская денежная и весовая единицы измерения подразделялись в силу исторических условий на 60 равных частей: 1 талант = 60 мин; 1 мина = 60 шекель. Шестидесятые доли были привычны в жизни вавилонян, поэтому они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или

его степени. Это первые в мире систематические дроби, то есть дроби, у которых знаменателем являются степени одного и того же числа. Пользуясь такими дробями, вавилоняне должны были многие дроби изображать приближенно. В этом недостаток и в то же время преимущество этих дробей. Эти дроби стали постоянным орудием научных вычислений греческих, а затем арабоязычных и средневековых европейских ученых вплоть до XV века, пока не уступили место десятичным дробям. Но шестидесятеричными дробями пользовались в астрономии ученые всех народов вплоть до XVII, называя их астрономическими дробями.

1.3 Дроби в Древнем Риме

Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию (2/3 унции, т.е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас. [2, 4] .

1.4 Дроби в Древнем Египте

Древний Египет славился высокоразвитой архитектурой. Это требовало точности в вычислениях длины, площади, объема и т.д. При изучении записей

на папирусах, ученые узнали, что египтяне 4000 лет назад имели десятичную систему счисления, умели решать задачи, связанные со строительством, торговлей, военным делом. На протяжении многих веков египтяне именовали дроби “ломаным числом”, а первая дробь, с которой они познакомились, была 1/2. За ней последовали 1/4, 1/8, 1/16, и так далее, затем 1/3, 1/6, и так далее. Это были самые простые дроби и называли их единичными дробями, у которых числитель равен единице (которые мы называем «долями»). Математики называют такие дроби аликвотными (от лат. aliquot – несколько). Так же используется название основные дроби или единичные дроби.

Египтяне ставили иероглиф (ер, «[один] из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. К примеру:

Египтяне использовали только две дроби не являющиеся долями – две трети и три четверти. Эти дроби часто встречались в вычислениях. Для них существовали специальные символы, был специальный знак и для дроби 1/2.

Кроме того, египтяне использовали формы записи, основанные на иероглифе Глаз Гора (Уаджет). Для древних характерно переплетение образа Солнца и глаза. В египетской мифологии часто упоминается бог Гор, олицетворяющий крылатое Солнце и являющийся одним из самых распространенных сакральных символов. В битве с врагами Солнца, воплощенными в образе Сета, Гор сначала терпит поражение. Сет вырывает у него Глаз — чудесное око — и разрывает его в клочья. Тот — бог учения, разума и правосудия — снова сложил части глаза в одно целое, создав «здоровый глаз Гора». Изображения частей разрубленного Ока использовались при письме в Древнем Египте для обозначения математических дробей. [1,4]

1.5 Дроби в Древней Греции

Египетские дроби продолжали использоваться в древней Греции, но греки считали, что дроби можно использовать только в логистике (искусство исчисления). Они свободно оперировали всеми арифметическими действиями с дробями, хотя числами их не признавали. В греческих сочинениях по математике дробей не встречалось. Греческие ученые считали, что математика должна заниматься только целыми числами. Возиться с дробями они предоставляли купцам, ремесленникам, а также астрономам, землемерам, механикам и другому «черному люду». «Если ты захочешь делить единицу,

математики высмеют тебя и не позволят это делать»,- писал основатель афинской академии Платон. Но не все древнегреческие математики соглашались с Платоном. С дробями свободно обращался Архимед и Герон Александрийский. Впервые в Древней Греции встречается понятие обыкновенной дроби вида .

Первый русский математик, известный как монах Новгородского монастыря, Кирик занимался вопросами хронологии и календаря. В его рукописной книге «Учение им же ведати человеку числа всех лет» (1136 г.), то есть «Наставление, как человеку познать счисление лет» применяется деление часа на пятые, двадцать пятые и т.д. доли, которые он называл «дробными часами» или «часцами». Доходит он до седьмых дробных часов, которых в дне или ночи 937 500, причем говорит, что от седьмых дробных уже ничего не получается. [4]

В первых учебниках математики (VII в.) дроби называли долями, позднее «ломаными числами». Происходит слово «дробь» от слов «дробить, разбивать, ломать на части». При записи числа использовалась горизонтальная черта,

1.7 Дроби в других государствах древних и средних веков

В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.

Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Зато вся дробь помещалась в прямоугольную рамку. Иногда использовалось и «трехэтажное» выражение с тремя числами в одной рамке; в зависимости от контекста это могло обозначать неправильную дробь (a + b/c) или деление целого числа a на дробь b/c. Правила действий над дробями почти не отличались от современных правил.

Записывать дроби как сейчас стали арабы, использовали три системы записи дробей. Во-первых, на индийский манер записывая знаменатель под числителем; дробная черта появилась в конце XII – начале XIII веков. Во-вторых, чиновники, землемеры, торговцы пользовались исчислением аликвотных дробей, похожим на египетские, при этом применялись дроби со знаменателями, не превышающими 10 (только для таких дробей арабский язык имеет специальные термины); часто использовались приближенные значения; арабские ученые работали над усовершенствованием этого исчисления. В-третьих, арабские ученые унаследовали вавилонско-греческую шестидесятеричную систему, в которой, как и греки, применяли алфавитную запись, распространив ее и на целые части. [1, 4]

2. Практическое применение дробей

2.1 Решение нестандартных задач

Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач, в том числе пришедших из глубины веков. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого.

В папирусе Ахмеса есть задача: «Разделить 7 хлебов между 8 людьми». Если резать каждый хлеб на 8 частей, придётся провести 49 разрезов.

Но складывать такие дроби было неудобно. Ведь в оба слагаемых могут входить одинаковые доли, и тогда при сложении появится дробь вида 2/n. А таких дробей египтяне не допускали. Поэтому, папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде суммы долей. И таких задач достаточно много. [1]

2.2 Исследование «Из глубины веков»

Цель исследования : провести исследование среди учащихся 6 – 8 классов с целью определения знаний у ребят о появлении дробей и важности их изучения, повышения заинтересованности учащихся при изучении дробей.

В исследовании приняли участие : 20 учащихся

1. Откуда пришли к нам дроби? (Из Древнего Египта)

2. От какого глагола происходит слово дробь? (Дробить, ломать, разбивать)

3.Какие виды дробей вы знаете? (Единичные, систематические, обыкновенные)

4. Нужны дроби в жизни любого человека и для чего? (Для более точного счёта).

5. Что показывает числитель и знаменатель дроби?

6. Что означает выражение «Он скрупулёзно изучил этот вопрос»? (Это означает, что вопрос изучен до конца, что не одной самой малой неясности не осталось. А происходит странное слово «скрупулёзно» от римского названия 1/288 асса – «скрупулус».)

7. Что означает выражение «Попасть в дроби»? (Это выражение означает попасть в трудное положение.)

Вывод. Из опроса видно, что более половины учащихся (58%) не знают историю появления дробей. Ребята понимают о необходимости применения дробей в жизни человека, но 25% называют узкий круг областей использования дробей. 20% ребят могут применять в своем лексиконе выражения, связанные с дробями. Таким образом, успешное применение дробей зависит от повышения заинтересованности учащихся при изучении дробей. Этот вывод сделан вместе с учителем и ребятами.

Во все времена и у всех народов учение о дробях считалось трудным разделом математики, для некоторых невыполнимой работой. Это отражено в словах основателя афинской академии Платона: «Если ты захочешь делить единицу, математики высмеют тебя и не позволят это делать». Но жизнь показала совсем другое отношение к дробям. Кто знал дроби, тот был в почете. “Без знания дробей никто не может признаваться знающим арифметику!” – говорил выдающийся римский оратор и писатель Цицерон в I веке до нашей эры. Другой автор одной из старинных славянских рукописей XV века пишет: «Несть се дивно, что …в целых, но есть похвально, что в долях…». [1]

Обыкновенные дроби необходимы, они важны в практической деятельности каждого человека. Характерен следующий отрывок из произведения знаменитого римского поэта I века до нашей эры Горация, о беседе учителя с учеником в одной из римских школ той эпохи:

— Учитель: Пусть скажет Сын Альбина, сколько останется, если от пяти унций отнять одну унцию!

— Учитель: Правильно, ты хорошо знаешь дроби и сумеешь сберечь своё имущество. [1]

Работая на этой темой, делаю вывод, что история обыкновенных дробей – это долгая кропотливая работа не только гениальных ученых – математиков, но и всего народа с его богатым жизненным опытом. Узнал много нового и интересного, читал дополнительную литературу, разделы из энциклопедий, статьи в сети Интернет. Познакомился с историей возникновения первых дробей, с понятием аликвотная и систематическая дроби, узнал имена ученых, внесших свой вклад в развитие учения о дробях. При этом встретилось много интересных старинных задач на действия с дробями, но решение некоторых мне не совсем были понятны, потому что действия с дробями мне предстоит еще узнать. Предполагаю продолжить работу по применению дробей в различных профессиях и в жизненных ситуациях.

Считаю, что цель и задачи моего исследования достигнуты. Материал, собранный мною в процессе работы можно использовать для расширения знаний учащихся о дробях, для поддержания интереса к изучению математики, используя презентацию по работе, в написании которой большую помощь оказали учителя и ребята.

Список источников информации

1. Валах В.Я. Путешествие в мир чисел, Киев, «Советская школа», 1978, 99 с.

2. Детская энциклопедия «Я познаю мир». Математика.- М.: ООО «Издательство АСТ-ЛТД», 1998. – 480 с.

Источник