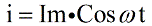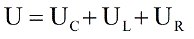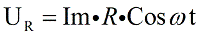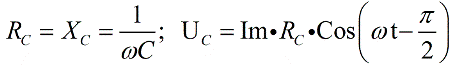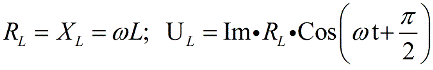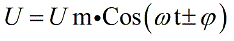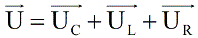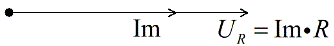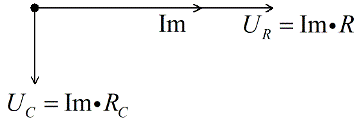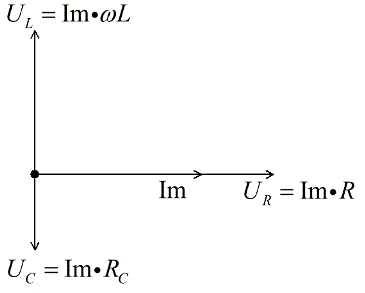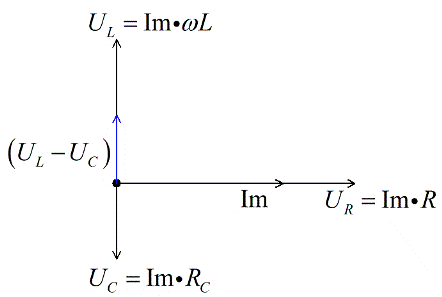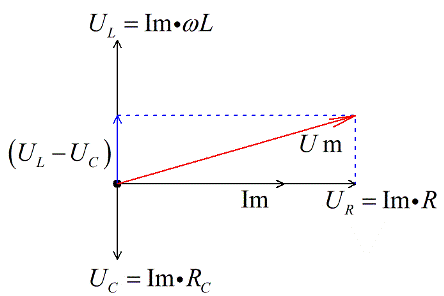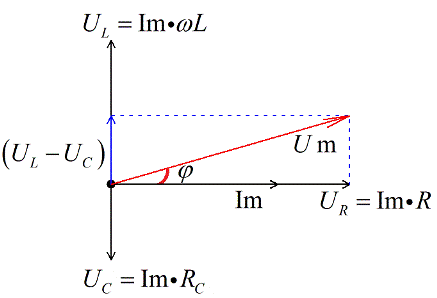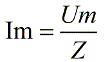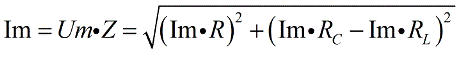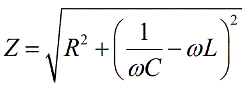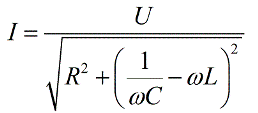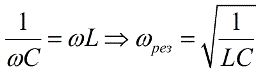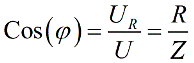Как построить векторную диаграмму токов и напряжений

Векторные диаграммы — метод графического расчета напряжений и токов в цепях переменного тока, в которых переменные напряжения и токи символически (условно) изображаются с помощью векторов.

Поэтому всякое переменное напряжение (или переменный ток), меняющееся по синусоидальному закону, можно изображать с помощью такого вектора, вращающегося с угловой скоростью, равной угловой частоте изображаемого тока, причем длина вектора в определенном масштабе изображает амплитуду напряжения, а угол — начальную фазу этого напряжения.

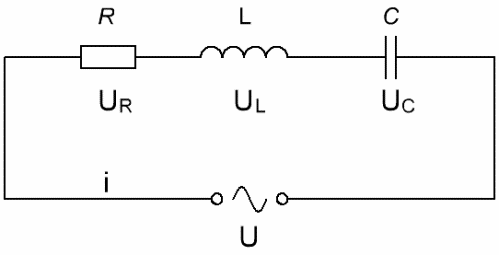
Если рассмотреть электрическую цепь, состоящую из последовательно соединенных источника переменного тока, резистора, индуктивности и конденсатора, где U – мгновенное значение переменного напряжения, а i – это ток в текущий момент времени, причем U изменяется по синусоидальному (косинусоидальному) закону, то для тока можно записать:

Согласно закону сохранения заряда, в любой момент времени ток в цепи имеет одно и то же значение. Следовательно на каждом элементе будет падать напряжение: UR– на активном сопротивлении, UC – на конденсаторе, и UL – на индуктивности. Согласно второму правилу Кирхгофа, напряжение источника будет равно сумме падений напряжений на элементах цепи, и мы имеем право записать:

Заметим, что согласно закону Ома: I = U/R, и тогда U = I*R. Для активного сопротивления значение R определяется исключительно свойствами проводника, оно не зависит ни от тока, ни от момента времени, следовательно ток совпадает по фазе с напряжением, и можно записать:

Можно записать теперь сумму падений напряжений, но в общем виде для приложенного к цепи напряжения можно записать:

Видно, что здесь имеет место некий сдвиг фаз, связанный с реактивной составляющей общего сопротивления цепи при протекании по ней переменного тока.

Поскольку в цепях переменного тока и ток и напряжение изменяются по закону косинуса, причем мгновенные значения отличаются между собой лишь фазой, то физики придумали в математических расчетах рассматривать токи и напряжения в цепях переменного тока как векторы, поскольку тригонометрические функции можно описать через векторы. Итак, запишем напряжения в виде векторов:

Используя метод векторных диаграмм, можно вывести, например, закон Ома для данной последовательной цепи в условиях протекания по ней переменного тока.

Согласно закону сохранения электрического заряда, в любой момент времени ток во всех частях данной цепи одинаков, так отложим же векторы токов, построим векторную диаграмму токов:

Пусть в направлении оси Х будет отложен ток Im – амплитудное значение тока в цепи. Напряжение на активном сопротивлении совпадает по фазе с током, значит эти векторы будут сонаправленными, отложим их из одной точки.

Напряжение на конденсаторе отстает на Пи/2 от тока, следовательно откладываем его под прямым углом вниз, перпендикулярно вектору напряжения на активном сопротивлении.

Напряжение на катушке опережает на Пи /2 ток, следовательно откладываем его под прямым углом вверх, перпендикулярно вектору напряжения на активном сопротивлении. Допустим, что для нашего примера UL>UC.

Поскольку мы имеем дело с векторным уравнением, сложим векторы напряжений на реактивных элементах, и получим разницу. Она будет для нашего примера (мы приняли что UL>UC) направлена вверх.

Прибавим теперь вектор напряжения на активном сопротивлении, и получим, по правилу векторного сложения, вектор суммарного напряжения. Так как брали максимальные значения, то и получим вектор амплитудного значения общего напряжения.

Так как ток менялся по закону косинуса, то напряжение тоже меняется по закону косинуса, но со сдвигом фаз. Между током и напряжением есть постоянный сдвиг фаз.

Запишем закон Ома для общего сопротивления Z (импеданса):

Из векторных изображений по Теореме Пифагора можем записать:

После элементарных преобразований получим выражение для полного сопротивления Z цепи переменного тока, состоящей из R, C и L:

Тогда получим выражение для закона Ома для цепи переменного тока:

Заметим, что наибольшее значение тока получатся в цепи при резонансе в условиях, когда:

Косинус фи из наших геометрических построений получается:

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Векторная диаграмма токов и напряжений

Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.

Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.

Определение

Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.

Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.

Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.

Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.

Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.

Разновидности

Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:

Векторную диаграмму токов можно построить 2 разными способами:

Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.

Построение

Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.

Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.

Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.

Способ 2

Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:

Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.

Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.

Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:

Далее нужно сделать:

Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.

Заключение

Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.

Видео по теме

Источник

Векторная диаграмма токов и напряжений

Большинство физических процессов имеют динамический характер, когда измеряемые параметры (напряжение электрического поля, сила тока, отклонения маятника или струны) изменяются во времени с определённой частотой повторения. Математический аппарат, применяемый для описания таких колебательных явлений, базируется на использовании гармонических функций, имеющих синусоидальный (или косинусоидальный) вид.

Оказалось, что гармонические колебания можно наглядно описывать в графическом виде с помощью векторных диаграмм (ВД). Колебательный процесс представляется в виде проекции вращающегося вектора на координатную ось (обычно на ось абсцисс Х в прямоугольной системе координат).

Разновидности векторных диаграмм

Основные понятия и обозначения

Колебания — это повторяющийся процесс изменения какой-либо системы (механической, электрической, акустической, тепловой, оптической) вблизи точки равновесия. Типичные примеры:

В общем виде гармоническое колебание описывается формулой:

Когда возникает задача сложения нескольких колебаний, то аналитическое (в виде формул) представление не позволяет судить о действующих соотношениях величин, так как они являются функциями времени. Изображение колебаний (величин A(t)) в виде векторов на плоскости, позволяет добиться наглядности и упрощает анализ количественных параметров системы. При этом колебания совершает проекция на ось абсцисс радиуса-вектора величины A(t) в данный момент времени.

Пускай имеется система, в которой есть два гармонических колебания B₁(t), B₂(t) с равными частотами ω₀. Например, это могут быть токи в электрической цепи или колебания грузиков на пружинках в механической системе. Чтобы получить суммарное колебание, необходимо сложить два выражения: B₁(t) = B₁ * cos(ω₀ * t + φ₁) и B₂(t) = B₂ * cos(ω₀ * t + φ₂)

Отложим на плоскости вектора B₁ и B₂ (см. Рис.2). Сумма этих векторов равна:

Видно, что векторное представление позволяет суммировать несколько колебаний с помощью наглядной процедуры сложения векторов.

Типы ВД

Существует два основных типа диаграмм: точные и качественные.

Качественные ВД являются одним из основных инструментов при анализе электрических цепей, наглядно иллюстрирующие положение искомого вектора.

ВД в комплексном представлении

Кроме алгебраической формы, применяется ещё два варианта записи: Z =|Z| * cos⁡(φ)+ i * sin⁡(φ) — тригонометрический, Z = |Z| * e iφ — показательный.

Последний вариант называется формулой Эйлера в честь великого математика, который предложил и обосновал эту формулу в XVIII веке. Комплексное представление гармонических колебаний позволяет упростить сложные тригонометрические вычисления наглядными и менее громоздкими действиями с показательными функциями. Графические ВД, рассмотренные ранее, можно считать аналогом (вариантом) представления гармонических колебаний с помощью комплексных чисел.

Примеры применения

Гармонический осциллятор в механике

Механическая система, будучи выведенная из равновесия, при определённых условиях начинает совершать гармонические колебания под действием возвращающей силы. Такая система называется гармоническим осциллятором. Классические примеры механического осциллятора:

Системы, в которых происходят гармонические колебания, имеют два основных признака:

С помощью универсального уравнения удаётся описать не только механические явления, но и акустические колебания, и электрические (переменный ток, напряжение), а также колебания электронов внутри атомов. Решения данного уравнения представляют собой выражения аналогичные: X(t) = X₀ * sin⁡(ω * t +φ₀) или X(t) = X₀ * cos⁡(ω * t + φ₀)

Свободные гармонические колебания без затухания

Из выражений следует, что гармонический осциллятор совершает свободные гармонические колебания с частотой: ω₀ = √(k/m). Период колебаний: T = 2*π* √(m/k), где π=3,14. Свободные гармонические колебания в графическом представлении с помощью ВД изображаются вращающимся с частотой ω₀ вектором А (Рис.4).

Гармонический осциллятор с затуханием и внешней вынуждающей силой

Гораздо чаще требуется решать задачи, в которых на осциллятор накладывается действие внешней силы, а также имеет место затухание колебаний в связи с наличием силы трения.

Из высшей математики известно, что любую функцию можно представить (разложить) в виде ряда или интеграла Фурье. Значит, решение уравнения может быть сведено к решению с синусоидальной силой:

Метод ВД в данном случае применяется в следующей последовательности:

Чтобы ускорение было направлено к точке равновесия, необходимо выполнение двух условий для выполнения составляющих (радиальной f_r и перпендикулярной f_p) сил и ускорения по оси вдоль радиуса-вектора по оси ей перпендикулярной. Два условия дают два уравнения:

В результате решения данных уравнений получают выражение для амплитуды колебания при заданной величине вынуждающей силы f:

Из отношения компонент силы f_r и f_p можно найти тангенс угла, под которым вектор силы на ВД наклонён к радиусу-вектору. Таким образом, будет найден сдвиг фазы колебаний x относительно фазы колебаний внешней силы f.

Метод ВД для расчёта электрических цепей

Чаще всего метод ВД применяется при расчётах электрических цепей. В принципе использование комплексного представления для гармонических колебаний более эффективно, чем классическое построение ВД, так как позволяет анализировать схемы любой сложности, состоящие из резисторов, индуктивностей и конденсаторов. К достоинствам ВД следует отнести доступность в приобретении навыков расчёта, в то время как математический аппарат комплексных чисел требует дополнительных знаний.

Самые распространённые случаи использования ВД для анализа — электрические схемы, в которых применяются пассивные элементы: резисторы, конденсаторы, индуктивности. С помощью ВД получается расчётная формула, при этом сама ВД выполняет роль чертежа-схемы, геометрическим способом иллюстрирующего поведение токов в цепи.

Для того чтобы не использовать комплексное представление, было введено понятие реактивного сопротивления конденсаторов и катушек индуктивностей. Это связано с физическими особенностями протекания переменного тока через эти схемные элементы. Основные формулы, связывающие токи и падения напряжений на элементах:

Напряжение на индуктивности будет:

Формулы для вычисления напряжений на конденсаторе и индуктивности напоминают классический закон Ома за исключением двух отличий:

На основании последних двух формул вводится понятие реактивного сопротивления Z:

Z_C = 1/ωC — реактивное емкостное сопротивление.

Z_C = ωL — реактивное индуктивное сопротивление.

Преобразование Фурье

Преобразование Фурье — это математическая операция, позволяющая разложить функцию с вещественной переменной на отдельные составляющие — гармонические колебания с разными частотами. Хорошей аналогией в данном случае служит аккорд на музыкальном инструменте, который состоит из нескольких отдельных звуков (нот) определённой частоты. На выходе преобразования получается набор частот (спектр), присутствующих в сигнале и пропорции амплитудных величин.

Преобразование Фурье вещественной функции u(t) задаётся следующей формулой:

где: u(t) — исходный сигнал, U(f) — изображение по Фурье, параметром которого выступает частота.

Эта математическая операция разлагает исходный сигнал на гармонические составляющие (гармоники). При исследованиях частотных спектров применение ВД в некоторых случаях позволяет получить результаты с хорошей точностью простыми средствами. Помимо этого, ВД полезны в иллюстративном плане для качественного понимания формальных вычислений.

Дифракция

Дифракцией в физике называют отклонение световых (электромагнитных) волн от распространения по законам геометрической оптики. При определённых соотношениях длины волны и параметров среды наблюдаются отклонения от прямолинейного распространения, возникает огибание препятствий и проникновение света в область геометрической тени.

Частным случаем является дифракция Фраунгофера (дифракция в параллельных лучах), когда световой источник и точка, где проводятся измерения (наблюдения), бесконечно удалены от препятствия, вызвавшего дифракцию. Как и в предыдущих случаях возникает задача суммирования синусоидальных волн с равными амплитудами, но сдвинутых по фазе на одинаковую величину (предыдущая с последующей). Фазовые сдвиги пропорциональны синусу угла.

Значит, может использоваться метод ВД, в котором каждая синусоида будет представлена вектором. В результате образуется ломаная линия, вписанная в окружность. Переходя к пределу, получится дуга окружности. Суммирующий вектор — это хорда полученной дуги, длина которой рассчитывается по известным геометрическим формулам.

С помощью ВД возможно качественно изучить переход от чисто фраунгоферового случая к более реальному, когда точка наблюдения приближается к щели. Длины векторов становятся неравными, но примерно можно оценить, как изменяется картина, пока расстояние уменьшилось не очень сильно.

Построение ВД напряжений и токов

В качестве примера построения ВД рассмотрим последовательную цепочку из сопротивления R, индуктивности L и конденсатора C. Схема приведена на рисунке ниже.

Напряжения на элементах схемы — U_R, U_L, U_C. Ток в цепи — i.

Пускай в цепи протекает синусоидальный ток с частотой ω и с нулевым сдвигом фазы. Для ненулевого сдвига фазы ВД просто повернётся на этот начальный угол, а общий её вид не изменится. Амплитуды напряжений на каждом элементе в форме закона Ома:

Соответствующие этим амплитудам длины векторов наносятся на ВД. При этом каждый вектор наносится с учетом своего фазового сдвига. Суммарный вектор оказался равен U = U_R + U_L + U_C, но это теперь доказано геометрически на диаграмме.

Применив формулы, указанные выше, получим:

Можно вынести за скобки i₀ (амплитуда тока — длина вектора i), тогда:

Пользуясь последней формулой, можно вычислять амплитуду синусоидального напряжения. Полученные формулы справедливы для случая обратной задачи, когда требуется найти ток в цепи с известным источником напряжения.

Заключение

Приведённые примеры демонстрируют универсальность применения метода ВД для решения разных физических и технических задач. Синусоидальные, повторяющиеся процессы происходят и в других областях знаний (химических и биологических системах). Наглядность и простота использования хорошо сочетаются на начальном этапе обучения, позволяя в дальнейшем перейти к освоению более сложного аппарата комплексного представления гармонических сигналов.

Источник

Построение векторных диаграмм

Достаточно сложным и чаще всего не изучаемым аспектом темы переменный ток является метод построения векторных диаграмм. Анализируя вынужденные электромагнитные колебания, мы уже обсудили сдвиг тока и напряжения на реактивных сопротивлениях (катушка индуктивности и конденсатор) по сравнению с активным сопротивлением (резистор). Тогда одним из задаваемых вопросов задачи является вопрос о направлении суммарного тока или напряжения в данный конкретный момент времени. Для ответа на этот вопрос и используется метод построения векторных диаграмм.

Векторная диаграмма — это изображение гармонически изменяющихся величин (текущего тока и напряжения) в виде векторов на плоскости.

Рис. 1. Векторная диаграмма

Построение векторных диаграмм происходит в прямоугольной декартовой системе координат. Построение начинается с проведения вектора, численно равного амплитудному значению тока в цепи. Данный вектор сонаправим в осью ОХ (рис. 1.1).

Т.к. напряжение на активном сопротивлении находится в одной фазе с током, то вектор амплитуды напряжения сонаправлен с вектором тока (рис. 1.2. красный).

На катушке напряжение опережает ток, поэтому отложим вектор амплитуды напряжения на катушке ( ) вверх под углом относительно вектора тока (рис. 1.2. синий).

На конденсаторе напряжение отстаёт от тока, поэтому отложим вектор амплитуды напряжения на конденсаторе ( ) вниз под углом относительно вектора тока (рис. 1.2. зелёный).

Для построения общего вектора напряжения достаточно векторно сложить напряжения:

Проще всего сначала найти вектор-сумму (т.к. они расположены вдоль одной прямой). В нашем случае, эти вектора разнонаправлены, найдём (рис. 1.3. жёлтый).

И последнее, осталось сложить получившийся вектор с вектором для получения значения полного напряжения в цепи (рис. 1.4. оранжевый). Для получения модуля вектора воспользуемся теоремой Пифагора, т.к. вектора находятся под прямым углом. Тогда:

Угол — угол между вектором силы тока и полного напряжения называется сдвигом фаз между колебаниями силы тока и напряжения. Данный параметр можно найти и исходя из параметров системы:

Вывод: задачи на данную тематику касаются поиска сдвига фаз между колебаниями силы тока и напряжения через график (рис. 1.4) или через соотношение (3), а также поиска полного напряжения в цепи также через график (рис. 1.4) или через соотношение (2).

Источник