Как построить угол между плоскостями
Угол между двумя пересекающимися плоскостями: определение, примеры нахождения
Статья рассказывает о нахождении угла между плоскостями. После приведения определения зададим графическую иллюстрацию, рассмотрим подробный способ нахождения методом координат. Получим формулу для пересекающихся плоскостей, в которую входят координаты нормальных векторов.
Угол между плоскостями – определение
В материале будут использованы данные и понятия, которые ранее были изучены в статьях про плоскость и прямую в пространстве. Для начала необходимо перейти к рассуждениям, позволяющим иметь определенный подход к определению угла между двумя пересекающимися плоскостями.
Рассмотрим не рисунке, приведенном ниже.
Рассмотрим рисунок, приведенный ниже.
Нахождение угла между двумя пересекающимися плоскостями
Обычный способ для нахождения угла между пересекающимися плоскостями – это выполнение дополнительных построений. Это способствует определять его с точностью, причем делать это можно с помощью признаков равенства или подобия треугольника, синусов, косинусов угла.
Для наглядности необходимо выполнить чертеж. Получим, что
Наглядное представление необходимо для того, чтобы было удобней работать с углом между плоскостями.
Рассмотрим на рисунке, приведенном ниже.
Получаем, что A M = A B · A F B F = 2 · 4 2 5 = 4 5 5
t g ∠ A M E = A E A M = 4 4 5 5 = 5
Некоторые случаи нахождения угла между пересекающимися прямыми задаются при помощи координатной плоскости О х у z и методом координат. Рассмотрим подробней.
Вычисление угла между пересекающимися прямыми производится по формуле
α = a r c cos n 1 x · n 2 x + n 1 y · n 2 y + n 1 z · n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 · n 2 x 2 + n 2 y 2 + n 2 z 2
Необходимо произвести подстановку найденных координат в формулу вычисления угла через арккосинус. Получаем
Метод координат дает аналогичный результат.
Завершающая задача рассматривается с целью нахождения угла между пересекающимися плоскостями при имеющихся известных уравнениях плоскостей.
Необходимо подставить координаты нормальных векторов плоскостей в формулу вычисления искомого угла пересекающихся плоскостей. Тогда получаем, что
Углы между плоскостями. Как определить угол между плоскостями
При решении геометрических задач в пространстве часто встречаются такие, где необходимо рассчитать углы между разными пространственными объектами. В данной статье рассмотрим вопрос нахождения углов между плоскостями и между ними и прямой.
Прямая в пространстве
Известно, что совершенно любая прямая на плоскости может быть определена следующим равенством:

Направляющий вектор прямой показывает ее ориентацию в пространстве. Этот параметр принадлежит прямой. Поскольку существует бесконечное множество параллельных в пространстве векторов, то для однозначного определения рассматриваемого геометрического объекта необходимо также знать координаты точки, принадлежащей ему.
Предположим, что имеется точка P(x0; y0; z0) и направляющий вектор v¯(a; b; c), тогда уравнение прямой может быть задано следующим образом:
(x; y; z ) = P + α * v¯ или
(x; y; z) = (x0; y0; z0) + α * (a; b; c)
Это выражение называется параметрическим векторным уравнением прямой. Коэффициент α является параметром, который может принимать абсолютно любые действительные значения. Координаты прямой можно представить явно, раскрывая это равенство:

Уравнение плоскости
Известно несколько форм записи уравнения для плоскости в пространстве. Здесь же рассмотрим одну из них, которая чаще всего используется при расчете углов между двумя плоскостями или между одной из них и прямой.
Если известен некоторый вектор n¯(A; B; C), который перпендикулярен искомой плоскости, а также указана точка P(x0; y0; z0), которая принадлежит ей же, то общее уравнение для последней имеет вид:
Мы опустили вывод этого выражения, который является достаточно простым. Здесь лишь заметим, что, зная коэффициенты при переменных в уравнении плоскости, можно с легкостью найти все вектора, которые ей перпендикулярны. Последние называются нормалями и используются при расчетах углов между наклонной и плоскостью и между произвольными аналогами.
Расположение плоскостей и формула угла между ними
Допустим, имеются две плоскости. Какие существуют варианты их взаимного расположения в пространстве. Поскольку плоскость имеет два бесконечных размера и один нулевой, то возможны лишь два варианта их взаимной ориентации:

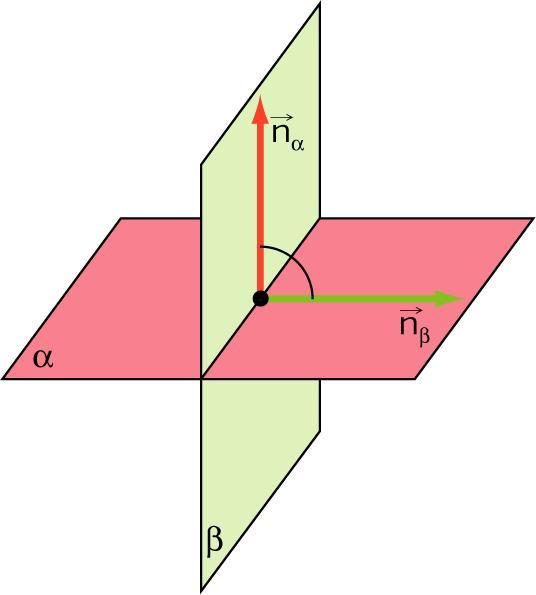
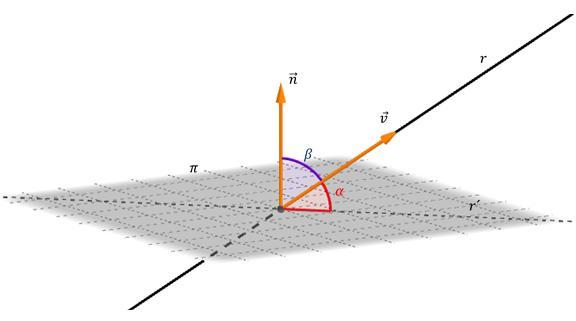
Углом между плоскостями называется показатель между их направляющими векторами, то есть между их нормалями n1¯ и n2¯.
Очевидно, что если являются параллельными плоскости, то угол пересечения равен нулю между ними. Если же они пересекаются, то он отличен от нуля, но всегда является острым. Частным случаем пересечения будет угол 90o, когда плоскости взаимно перпендикулярны друг другу.
Угол α между n1¯ и n2¯ легко определяется из произведения скалярного этих векторов. То есть имеет место формула:
α = arccos((n1¯ * n2¯)/(|n1¯| * |n2¯|))
Предположим, что координаты этих векторов следующие: n1¯(a1; b1; c1), n2¯(a2; b2; c2). Тогда, используя формулы для расчета скалярного произведения и модулей векторов через их координаты, выражение выше можно переписать в виде:
α = arccos(|a1 * a2 + b1 * b2 + c1 * c2| / (√(a12 + b12 + c12) * √(a22 + b22 + c22)))
Модуль в числителе появился потому, чтобы исключить значения тупых углов.
Примеры решения задач на определение угла пересечения плоскостей
Зная, как найти между плоскостями угол, решим следующую задачу. Даны две плоскости, уравнения которых имеют вид:
Чему между плоскостями равен угол?
Чтобы ответить на вопрос задачи, вспомним, что коэффициенты, стоящие при переменных в уравнении плоскости общем, являются координатами вектора направляющего. Для указанных плоскостей имеем следующие координаты их нормалей:
Теперь найдем произведение скалярное этих векторов и их модули, имеем:
Теперь можно подставить найденные числа в приведенную в предыдущем пункте формулу. Получаем:
α = arccos(|-16 | / (√26 * √30) ≈ 55,05o
Полученное значение соответствует острому углу пересечения плоскостей, указанных в условии задачи.
Теперь рассмотрим другой пример. Даны две плоскости:
Пересекаются ли они? Выпишем значения координат их направляющих векторов, посчитаем скалярное произведение их и модули:
(n1¯ * n2¯) = 3 + 3 + 0 = 6;
Тогда угол пересечения равен:
α = arccos(|6| / (√2 * √18) =0o.
Этот угол говорит о том, что плоскости не пересекаются, а являются параллельными. Тот факт, что они не совпадают друг с другом проверить просто. Возьмем для этого произвольную точку, принадлежащую первой из них, например, P(0; 3; 2). Подставим ее координаты во второе уравнение, получим:

3 * 0 +3 * 3 + 8 = 17 ≠ 0
То есть точка P принадлежит только первой плоскости.
Таким образом, две плоскости параллельными являются, когда таковыми будут их нормали.
Плоскость и прямая
В случае рассмотрения взаимного расположения между плоскостью и прямой существует несколько больше вариантов, чем с двумя плоскостями. Связан этот факт с тем, что прямая является одномерным объектом. Прямая и плоскость могут быть:
Рассмотрим сначала последний случай, поскольку он требует введения понятия об угле пересечения.
Прямая и плоскость, значение угла между ними
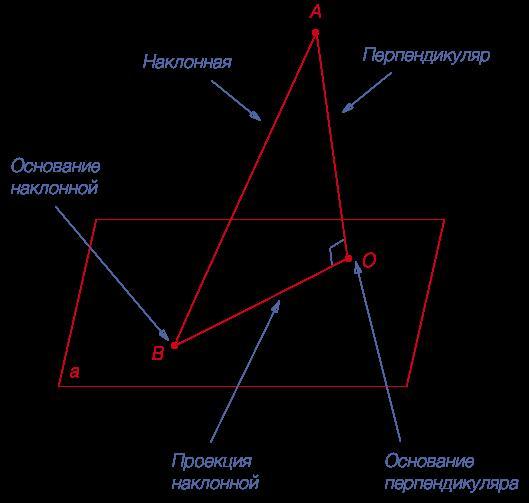
Если плоскость прямая пересекает, то она называется наклонной по отношению к ней. Точку пересечения принято называть основанием наклонной. Чтобы определить между этими геометрическими объектами угол, необходимо опустить из любой точки прямой перпендикуляр на плоскость. Тогда точка пересечения перпендикуляра с плоскостью и место пересечения с ней наклонной образуют прямую. Последняя называется проекцией исходной прямой на рассматриваемую плоскость. Острый угол между прямой и проекцией ее является искомым.
Несколько запутанное определение угла между плоскостью и наклонной прояснит рисунок ниже.
Чтобы записать формулу для него, рассмотрим пример. Пусть имеется прямая и плоскость, которые описываются уравнениями:
(x ; y ; z ) = (x0; y0; z0) + λ * (a; b; c);
A * x + B * x + C * x + D = 0
Рассчитать искомый угол для этих объектов можно легко, если найти скалярное произведение между направляющими векторами прямой и плоскости. Полученный острый угол следует вычесть из 90o, тогда он получается между прямой и плоскостью.
Выше была представлена формула, дающая ответ на вопрос, как между плоскостями найти угол. Теперь приведем соответствующее выражение для случая прямой и плоскости:
α = arcsin(|a * A + b * B + c * C| / (√(a 2 + b2 + c 2) * √(A 2 + B 2 + C 2)))
Модуль в формуле позволяет вычислять только острые углы. Функция арксинуса появилась вместо арккосинуса благодаря использованию соответствующей формулы приведения между тригонометрическими функциями (cos(β) = sin(90o-β) = sin(α)).
Задача: плоскость пересекает прямую
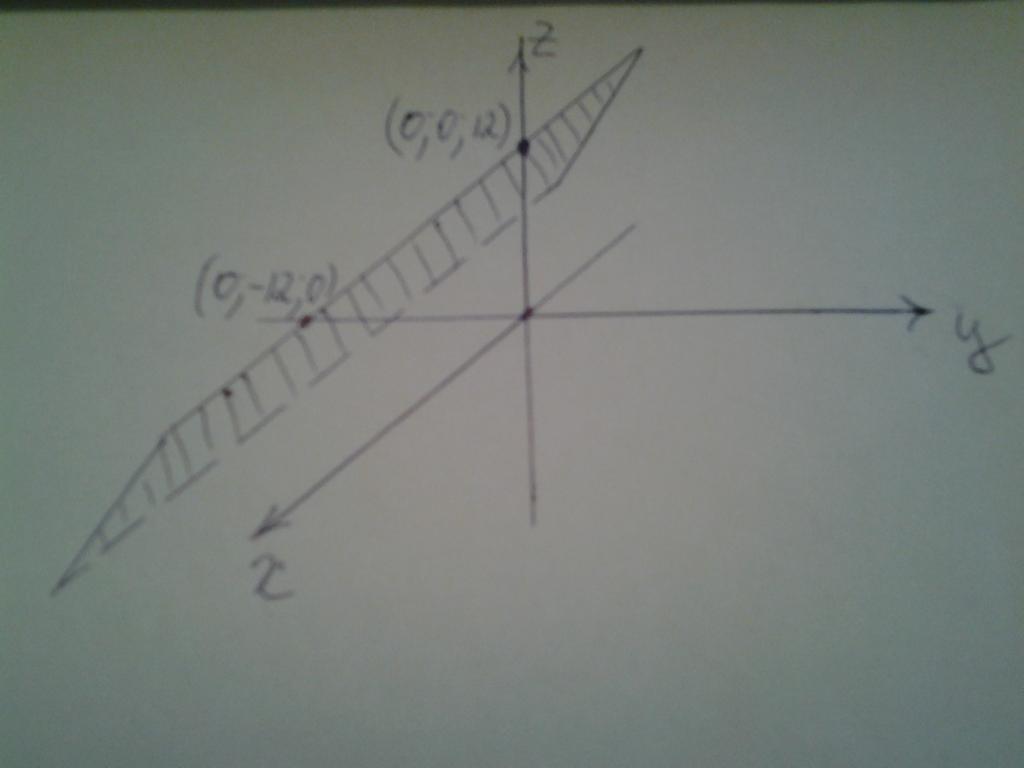
Теперь покажем, как работать с приведенной формулой. Решим задачу: необходимо вычислить угол между осью y и плоскостью, заданной уравнением:
Эта плоскость показана на рисунке.
α = arcsin(|1| / (√1 * √2)) = arcsin(1 / √2) = 45o
Задача: параллельная плоскости прямая
Теперь решим аналогичную предыдущей задачу, вопрос которой поставлен иначе. Известны уравнения плоскости и прямой:
(x; y; z) = (1; 0; 0) + λ * (0; 2; 2)
Необходимо выяснить, являются ли эти геометрические объекты параллельными друг другу.
Полученный ноль говорит о том, что угол между этими векторами равен 90o, что доказывает прямой и плоскости параллельность.
Теперь проверим, является эта прямая только параллельной или же еще и лежит в плоскости. Для этого следует выбрать произвольную точку на прямой и проверить, принадлежит ли она плоскости. Например, примем λ = 0, тогда точка P(1; 0; 0) прямой принадлежит. Подставляем в уравнение плоскости P:
Точка P плоскости не принадлежит, а значит, и вся прямая в ней не лежит.
Где важно знать углы между рассмотренными геометрическими объектами?
Приведенные выше формулы и примеры решения задач представляют собой не только теоретический интерес. Они часто применяются для определения важных физических величин реальных объемных фигур, например призмы или пирамиды. Важно уметь определить между плоскостями угол при расчете объемов фигур и площадей их поверхностей. При этом, если в случае прямой призмы можно не использовать эти формулы для определения указанных величин, то для любого вида пирамиды их применение оказывается неизбежным.
Ниже рассмотрим пример использования изложенной теории для определения углов пирамиды с квадратным основанием.
Пирамида и ее углы
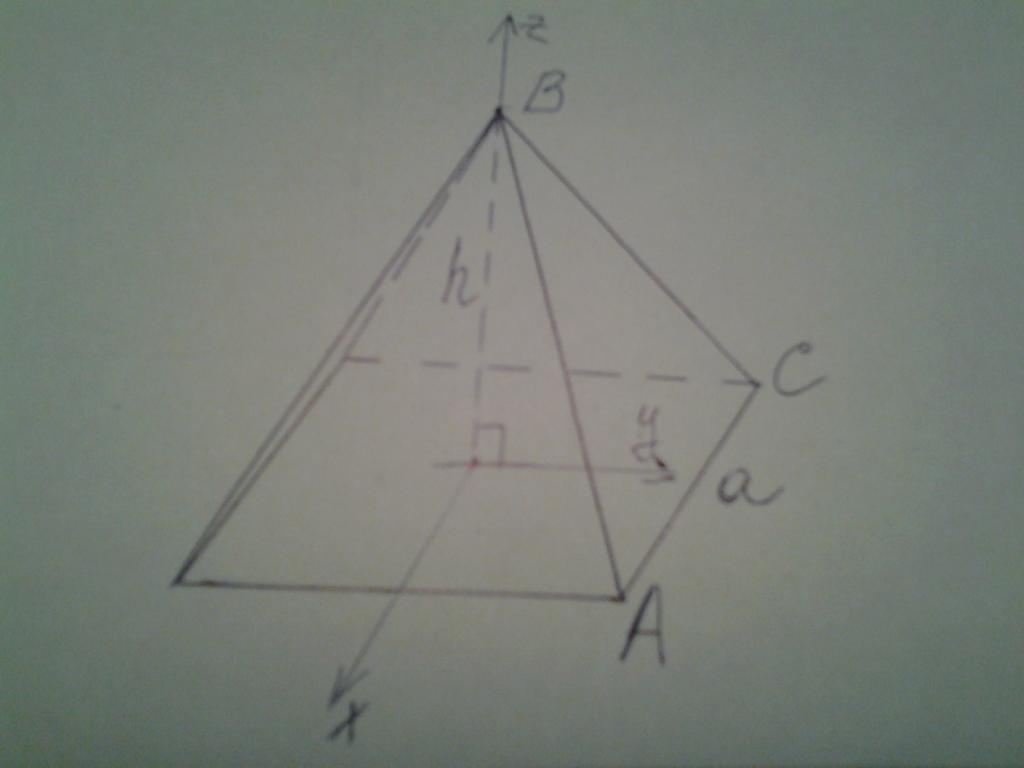
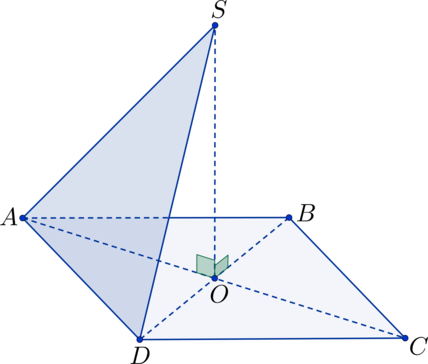
Ниже рисунок демонстрирует пирамиду, в основании которой лежит квадрат со стороной а. Высота фигуры составляет h. Нужно найти два угла:
Чтобы решить поставленную задачу, сначала следует ввести систему координат и определить параметры соответствующих вершин. На рисунке показано, что начало координат совпадает с точкой в центре квадратного основания. В этом случае плоскость основания описывается уравнением:
То есть для любых x и y значение третьей координаты всегда равно нулю. Боковая плоскость ABC пересекает ось z в точке B(0; 0; h), а ось y в точке с координатами (0; a/2; 0). Ось x она не пересекает. Это означает, что уравнение плоскости ABC можно записать в виде:
y / (a / 2) + z / h = 1 или
Вектор AB¯ является боковым ребром. Координаты его начала и конца равны: A(a/2; a/2; 0) и B(0; 0; h). Тогда координаты самого вектора:
Мы нашли все необходимые уравнения и вектора. Теперь остается воспользоваться рассмотренными формулами.
Рассчитаем сначала в пирамиде угол между плоскостями основания и боковой стороны. Соответствующие нормальные вектора равны: n1¯(0; 0; 1) и n2¯(0; 2*h; a). Тогда угол составит:
α = arccos(a / √(4 * h2 + a2 ))
Угол между плоскостью и ребром AB будет равен:
β = arcsin(h / √(a2 / 2 + h2 ))
Остается подставить конкретные значения стороны основания a и высоты h, чтобы получить необходимые углы.
Двугранный угол (ЕГЭ 2022)
Дай нам 10 минут ты разберешься в одной из самых важных тем стереометрии.
И получишь за неё баллы на ЕГЭ!
Двугранный угол — коротко о главном
Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.
Угол между плоскостями – наименьший из двугранных углов, образованных при пересечении плоскостей.
Двугранный угол может быть и острым и тупым, а угол между плоскостями только острым! НЕ ПУТАЙ!
Прямой двугранный угол – двугранный угол, который равен \( \displaystyle 90<>^\circ \), то есть тот, у которого линейный угол равен \( \displaystyle 90<>^\circ \).
Два способа найти угол между плоскостями:
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
Двугранный угол — определения
Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.
При этом прямая \( \displaystyle AB\) – это ребро двугранного угла, а полуплоскости \( \displaystyle \alpha \) и \( \displaystyle \beta \) – стороны или грани двугранного угла.
Двугранный угол получает обозначение по своему ребру: «двугранный угол \( \displaystyle AB\)».
С понятием двугранного угла тесно связано понятие угол между плоскостями.
Угол между плоскостями – наименьший из двугранных углов, образованных при пересечении плоскостей.
Итак, внимание! Различие между двугранным углом и углом между плоскостями в том, что:
Двугранный угол может быть и острым, и тупым, а угол между плоскостями только острым! НЕ ПУТАЙ!
Линейный угол двугранного угла
Как измерить двугранный угол?
Нужно поступить так: из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру.
В плоскости \( \displaystyle \alpha \) провели перпендикуляр \( \displaystyle MD\) к ребру \( \displaystyle AB\). Что получилось? Обычный, плоский угол \( \displaystyle \varphi \).
Вот этот угол и называется: линейный угол двугранного угла \( \displaystyle AB\).
Зачем этот линейный угол? Запомни, это очень ВАЖНО:
Двугранный угол измеряется величиной своего линейного угла.
То есть математически договорились, что если угол φ будет равен, к примеру \( \displaystyle 20<>^\circ \), то это будет автоматически означать, что угол \( \displaystyle AB\) равен \( \displaystyle 20<>^\circ \).
Вот и ключ к поиску величины двугранного угла и угла между плоскостями:
Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.
Ещё раз немного о названиях.
Прямой двугранный угол – двугранный угол, который равен \( \displaystyle 90<>^\circ \), то есть тот, у которого линейный угол равен \( \displaystyle 90<>^\circ \).
Как найти угол между плоскостями?
Найти угол между плоскостями можно двумя способами: геометрическим и алгебраическим.
Геометрический способ
При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.
Алгебраический способ
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
| \( \displaystyle \cos \gamma =\frac<<_<1>><_<2>>+<_<1>><_<2>>+< |
Подробнее про уравнение плоскости ты можешь прочитать в статье «Расстояние от точки до плоскости»!
Какой же способ лучше? Зависит от задачи.
А если линейный угол двугранного угла никак не хочет проходить ни через какие удобные точки, то можно использовать метод координат как палочку выручалочку.
Но тогда нужно очень твёрдо знать формулы и не делать арифметических ошибок при многочисленных подсчётах – ведь придётся искать \( \displaystyle <_<1>>,<_<1>>,<
Давай разберём несложную задачу для примера. Мы применим оба метода к одной и той же задаче.
Решение геометрическим способом
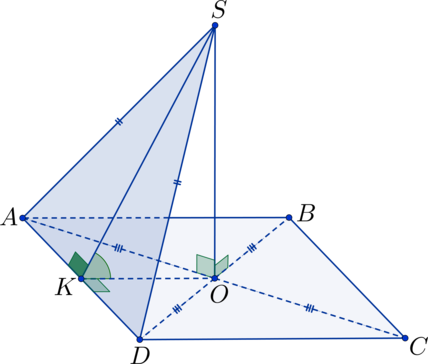
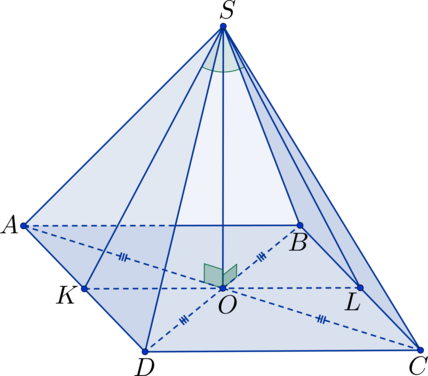
В правильной треугольной пирамиде боковое ребро в три раза больше ребра основания. Найти двугранный угол при основании пирамиды.
Нахождение угла между плоскостями (двугранный угол)
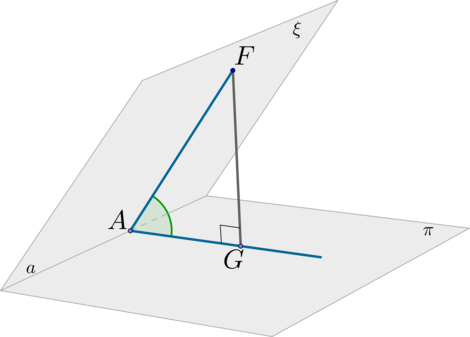
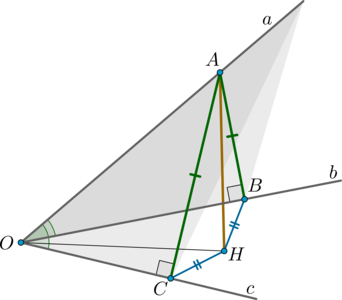
Шаг 1: пусть \(\xi\cap\pi=a\) (линия пересечения плоскостей). В плоскости \(\xi\) отметим произвольную точку \(F\) и проведем \(FA\perp a\) ;
Шаг 2: проведем \(FG\perp \pi\) ;
Шаг 3: по ТТП ( \(FG\) – перпендикуляр, \(FA\) –наклонная, \(AG\) – проекция) имеем: \(AG\perp a\) ;
Построим \(MN\) перпендикулярно \(AB\) как показано на рисунке.
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.
Вначале необходимо определить прямую, по которой пересекаются плоскости.
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.
Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.
Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.
Рекомендации о том, как найти угол между плоскостями
При решении стереометрических задач, где ключевым моментом является построение правильного чертежа, ученику необходимо иметь знания в области планиметрии и стереометрии.
При решении задач традиционным (геометрическим) методом у учеников возникают сложности в построении предполагаемого чертежа, дополнительных элементов, трудности в доказательных рассуждениях. Традиционный способ требует более точного построения и определения угла между плоскостями.
Использование «метода координат» при решении стереометрических задач на нахождение угла между двумя плоскостями
Встречаются такие задачи, в которых сложно построить сечения (плоскости) и определить линию пересечения плоскостей и найти такие прямые в данных плоскостях, которые будут перпендикулярны этой линии. В таких случаях на помощь приходит «метод координат».
В рамках данной статьи рассмотрим решение задач «методом координат» на нахождение угла между плоскостями. Данный метод алгоритмизирован и не требует построения искомого угла между плоскостями.
Для решения стереометрических задач ученик должен иметь теоретическую базу. Определения, теоремы и т.д. можно изучить в учебнике по геометрии Атанасяна Л.С. для 10-11 классов и Погорелова А.В. для 10-11 классов [1; 2]. Вспомним по данной теме основное определение:
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
Определение подсказывает традиционный метод нахождения угла между плоскостями. Для решения этим методом:
Но встречаются такие задачи, в которых сложно построить выше перечисленные элементы. «Метод координат» не требует построения угла между плоскостями и является универсальным методом, в котором заложен алгоритм нахождения данного угла.
Для этого необходимо составить уравнения плоскостей, для того чтобы найти их нормальные векторы. Далее находим косинус между этими векторами. Угол между этими векторами будет искомой величиной угла между плоскостями.

Найдем нормальные векторы данных плоскостей:
При решении данных задач, необходимо знать основную формулу. Она определят угол между плоскостями, как угол между нормалями данных плоскостей.
Двугранный угол. Подробная теория с примерами
Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
| Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой. |
Итак, внимание! Различие между двугранным углом и углом между плоскостями в том, что:
| Двугранный угол может быть и острым, и тупым, а угол между плоскостями только острым! НЕ ПУТАЙ! |
Как найти угол между плоскостями
Найти угол между плоскостями (можно двумя способами: геометрическим и алгебраическим).
При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
Нахождение угла между плоскостями (двугранный угол)
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями.
Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала.
Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ. Вначале необходимо определить прямую, по которой пересекаются плоскости.
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра. Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол. Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями.
Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо.
А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.
Угол между двумя пересекающимися плоскостями: определение, примеры нахождения, как найти угол между плоскостями
Статья рассказывает о нахождении угла между плоскостями. После приведения определения зададим графическую иллюстрацию, рассмотрим подробный способ нахождения методом координат. Получим формулу для пересекающихся плоскостей, в которую входят координаты нормальных векторов.
Угол между плоскостями – определение
В материале будут использованы данные и понятия, которые ранее были изучены в статьях про плоскость и прямую в пространстве. Для начала необходимо перейти к рассуждениям, позволяющим иметь определенный подход к определению угла между двумя пересекающимися плоскостями.
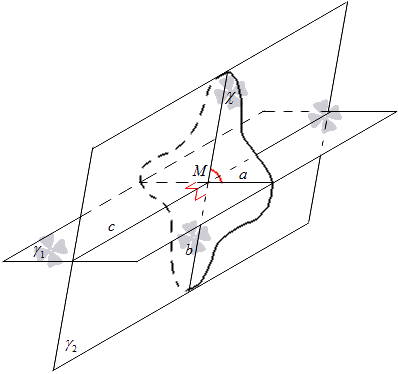
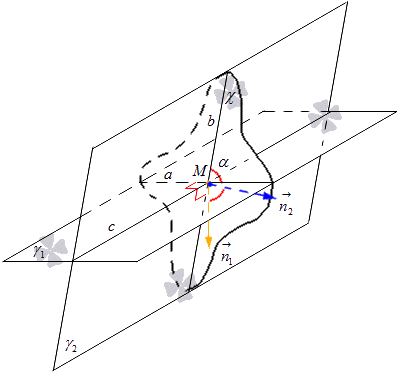
Заданы две пересекающиеся плоскости γ1 и γ2. Их пересечение примет обозначение c. Построение плоскости χ связано с пересечением этих плоскостей. Плоскость χ проходит через точку М в качестве прямой c.
Будет производиться пересечение плоскостей γ1 и γ2 с помощью плоскости χ. Принимаем обозначения прямой, пересекающей γ1 и χ за прямую a, а пересекающую γ2 и χ за прямую b.
Получаем, что пересечение прямых a и b дает точку M. Расположение точки M не влияет на угол между пересекающимися прямыми a и b, а точка M располагается на прямой c, через которую проходит плоскость χ.
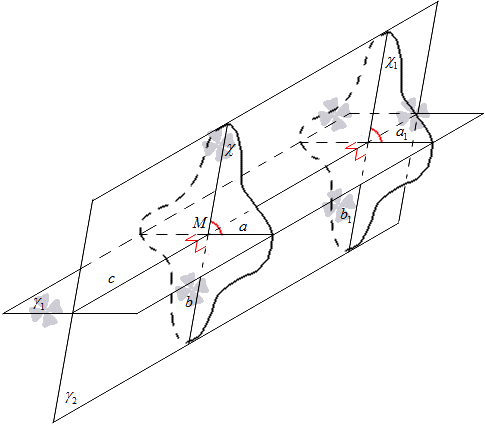
Необходимо построить плоскость χ1 с перпендикулярностью к прямой c и отличную от плоскости χ. Пересечение плоскостей γ1 и γ2 с помощью χ1 примет обозначение прямых а1 и b1.
Видно, что при построении χ и χ1 прямые a и b перпендикулярны прямой c, тогда и а1, b1 располагаются перпендикулярно прямой c. Нахождение прямых a и а1 в плоскости γ1 с перпендикулярностью к прямой c, тогда их можно считать параллельными.
Таки же образом расположение b и b1 в плоскости γ2 с перпендикулярностью прямой c говорит об их параллельности. Значит, необходимо сделать параллельный перенос плоскости χ1 на χ, где получим две совпадающие прямые a и а1, b и b1.
Получаем, что угол между пересекающимися прямыми a и b1 равен углу пересекающихся прямых a и b. Рассмотрим не рисунке, приведенном ниже.
Данное суждение доказывается тем, что между пересекающимися прямыми a и b имеется угол, который не зависит от расположения точки M, то есть точки пересечения. Эти прямые располагаются в плоскостях γ1 и γ2. Фактически, получившийся угол можно считать углом между двумя пересекающимися плоскостями.
Перейдем к определению угла между имеющимися пересекающимися плоскостями γ1 и γ2.
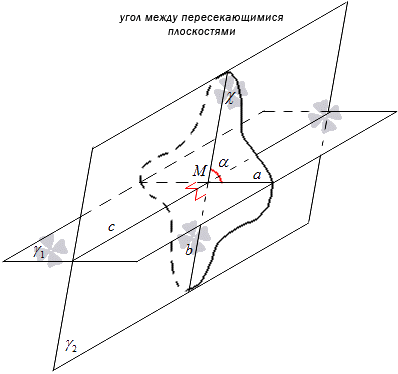
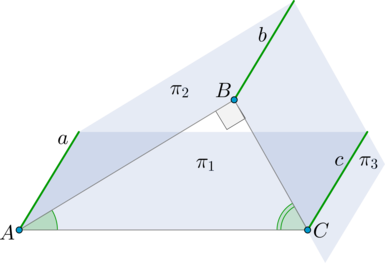
Углом между двумя пересекающимися плоскостями γ1 и γ2 называют угол, образовавшийся путем пересечения прямых a и b, где плоскости γ1 и γ2 имеют пересечение с плоскостью χ, перпендикулярной прямой c. Рассмотрим рисунок, приведенный ниже.
Определение может быть подано в другой форме. При пересечении плоскостей γ1 и γ2, где c – прямая, на которой они пересеклись, отметить точку M, через которую провести прямые a и b, перпендикулярные прямой c и лежащие в плоскостях γ1 и γ2, тогда угол между прямыми a и b будет являться углом между плоскостями. Практически это применимо для построения угла между плоскостями.
При пересечении образуется угол, который по значению меньше 90 градусов, то есть градусная мера угла действительна на промежутке такого вида (0, 90]. Одновременно данные плоскости называют перпендикулярнымив случае, если при пересечении образуется прямой угол. Угол между параллельными плоскостями считается равным нулю.
Нахождение угла между двумя пересекающимися плоскостями
Обычный способ для нахождения угла между пересекающимися плоскостями – это выполнение дополнительных построений. Это способствует определять его с точностью, причем делать это можно с помощью признаков равенства или подобия треугольника, синусов, косинусов угла.
Рассмотрим решение задач на примере из задач ЕГЭ блока C2.
Пример 1
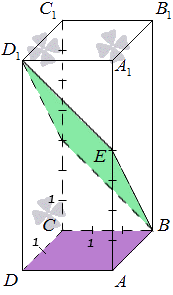
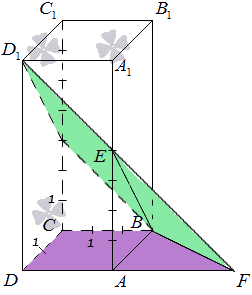
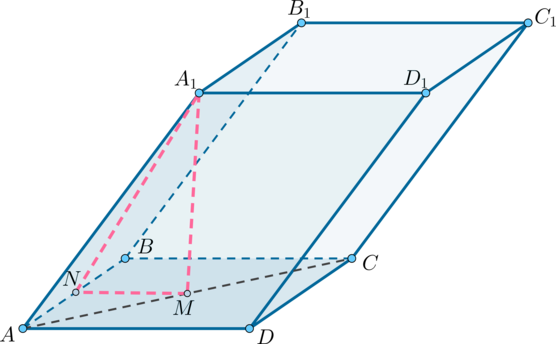
Задан прямоугольный параллелепипед АВСDA1B1C1D1, где сторона АВ=2, AD=3, АА1=7, точка E разделяет сторону АА1 в отношении 4:3. Найти угол между плоскостями АВС и ВED1.
Для наглядности необходимо выполнить чертеж. Получим, что наглядное представление необходимо для того, чтобы было удобней работать с углом между плоскостями.
Производим определение прямой линии, по которой происходит пересечение плоскостей АВС и ВED1. Точка B является общей точкой. Следует найти еще одну общую точку пересечения. Рассмотрим прямые DA и D1E, которые располагаются в одной плоскости ADD1. Их расположение не говорит о параллельности, значит, они имеют общую точку пересечения.
Однако, прямая DA расположена в плоскости АВС, а D1E в BED1. Отсюда получаем, что прямые DA и D1E имеют общую точку пересечения, которая является общей и для плоскостей АВС и BED1. Обозначает точку пересечения прямых DA и D1Eбуквой F. Отсюда получаем, что BF является прямой, по которой пересекаются плоскости АВС и ВED1.
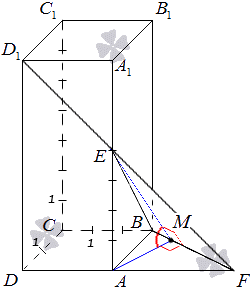
Для получения ответа необходимо произвести построение прямых, расположенных в плоскостях АВС и ВED1 с прохождением через точку, находящуюся на прямой BF и перпендикулярной ей. Тогда получившийся угол между этими прямыми считается искомым углом между плоскостями АВС и ВED1.
Отсюда видно, что точка A – проекция точки E на плоскость АВС. Необходимо провести прямую, пересекающую под прямым углом прямую BF в точке М. Видно, что прямая АМ – проекция прямой ЕМ на плоскость АВС, исходя из теоремы о тех перпендикулярах AM⊥BF. Рассмотрим рисунок, изображенный ниже.
∠AME — это искомый угол, образованный плоскостями АВС и ВED1. Из получившегося треугольника АЕМ можем найти синус, косинус или тангенс угла, после чего и сам угол, только при известных двух сторонах его.
По условию имеем, что длина АЕ находится таким образом: прямая АА1 разделена точкой E в отношении 4:3, то означает полную длину прямой – 7 частей, тогда АЕ= 4 частям. Находим АМ.
Необходимо рассмотреть прямоугольный треугольник АВF. Имеем прямой угол A с высотой АМ. Из условия АВ=2, тогда можем найти длину AF по подобию треугольников DD1F и AEF. Получаем, что AEDD1=AFDF⇔AEDD1=AFDA+AF⇒47=AF3+AF⇔AF=4
Необходимо найти длину стороны BF из треугольника ABF, используя теорему Пифагора. Получаем, что BF =AB2+AF2=22+42=25. Длина стороны АМ находится через площадь треугольника ABF. Имеем, что площадь может равняться как SABC=12·AB·AF, так и SABC=12·BF·AM.
Получаем, что AM=AB·AFBF=2·425=455. Тогда можем найти значение тангенса угла треугольника АЕМ. Получим:
Искомый угол, получаемый пересечением плоскостей АВС и BED1 равняется arctg5, тогда при упрощении получим arctg5=arcsin 306=arccos66.
Ответ: arctg5=arcsin 306=arccos66.
Некоторые случаи нахождения угла между пересекающимися прямыми задаются при помощи координатной плоскости Охуz и методом координат. Рассмотрим подробней.
Если дана задача, где необходимо найти угол между пересекающимися плоскостями γ1 и γ2, искомый угол обозначим за α.
Тогда заданная система координат показывает, что имеем координаты нормальных векторов пересекающихся плоскостей γ1 и γ2. Тогда обозначим, что n1→=n1x, n1y, n1z является нормальным вектором плоскости γ1, а n2→=(n2x, n2y, n2z) — для плоскости γ2. Рассмотрим подробное нахождение угла, расположенного между этими плоскостями по координатам векторов.
Необходимо обозначить прямую, по которой происходит пересечение плоскостей γ1 и γ2 буквой c. На прямой с имеем точку M, через которую проводим плоскость χ, перпендикулярную c. Плоскость χ по прямым a и b производит пересечение плоскостей γ1 и γ2 в точке M.
из определения следует, что угол между пересекающимися плоскостями γ1 и γ2 равен углу пересекающихся прямых a и b, принадлежащих этим плоскостям соответственно.
В плоскости χ откладываем от точки M нормальные векторы и обозначаем их n1→ и n2→. Вектор n1→ располагается на прямой, перпендикулярной прямой a, а вектор n2→ на прямой, перпендикулярной прямой b. Отсюда получаем, что заданная плоскость χ имеет нормальный вектор прямой a, равный n1→ и для прямой b, равный n2→. Рассмотрим рисунок, приведенный ниже.
Отсюда получаем формулу, по которой можем вычислить синус угла пересекающихся прямых при помощи координат векторов.
Получили, что косинусом угла между прямыми a и b то же, что и косинус между пересекающимися плоскостями γ1 и γ2 выводится из формулы cos α=cosn1→, n2→^=n1x·n2x+n1y·n2y+n1z·n2zn1x2+n1y2+n1z2·n2x2+n2y2+n2z2, где имеем, что n1→=(n1x, n1y, n1z) и n2→=(n2x, n2y, n2z) являются координатами векторов представленных плоскостей. Вычисление угла между пересекающимися прямыми производится по формуле: