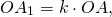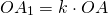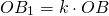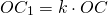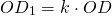Как построить треугольник гомотетичный данному
Гомотетия
Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу
где k — постоянное, отличное от нуля число, O — фиксированная точка.
Точка O называется центром гомотетии, число k — коэффициентом гомотетии.
гомотетия с коэффициентом k>0
Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:
и соединить вершины A1, B1, C1и D1 отрезками.
При k
и соединить вершины A1, B1, C1 отрезками.
При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.
Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.
Свойства преобразования гомотетии
1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.
2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).
Стороны гомотетичных фигур пропорциональны. а углы — равны.
Применение геометрических преобразований к решению задач
ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ЗАДАЧ
Ученики 10 класса хорошо знакомы, а ученики 9 класса уже познакомились с такими геометрическими преобразованиями плоскости как поворот вокруг некоторой точки на заданный угол, параллельный перенос, осевая и центральная симметрии. Наша задача: сделать небольшой шаг за рамки школьного учебника и изучить еще несколько замечательных преобразований плоскости. Начнем мы с гомотетии.
Определение 1. Гомотетией с центром в точке М0 и коэффициентом k называется правило, по которому каждая точка М отображается в точку М’, и при этом выполняется условие:

Две фигуры назовем гомотетичными, если одна может быть получена и другой с помощью некоторой гомотетии.
Рассмотрим примеры гомотетии с различными коэффициентами.
На первом рисунке построен образ треугольника АВС при гомотетии с коэффициентом 2, а на втором – приведен пример гомотетии с коэффициентом -2. Наблюдательный читатель сразу заметит, что на обоих чертежах изображены пары подобных треугольников. Причем в обоих случаях коэффициент подобия равен 2. Кроме того, хорошо видно, что соответствующие стороны треугольника АВС и треугольника А’В’С’ – попарно параллельны.
Сформулируем основные свойства гомотетии.
Свойство 1. При гомотетии точка отображается в точку, отрезок в отрезок, а прямая в прямую.
Свойство 2. Гомотетия сохраняет принадлежность объектов (инцидентность). Другими словами, если точка принадлежит некоторой фигуре, то ее образ будет принадлежать образу этой фигуры, и наоборот.
Свойство 3. Гомотетия сохраняет параллельность. То есть, две параллельные прямые отображаются в две параллельные прямые.
Свойство 4. Гомотетия прямую отображает в параллельную ей прямую.
Рассмотрим важное следствие их этих свойств.
Следствие 1. Гомотетия любую фигуру отображает в подобную ей, причем коэффициент подобия равен модулю коэффициента гомотетии.
Доказательство. Достаточно показать, что это утверждение выполняется для треугольников. (Используем следующий признак подобия: два треугольника подобны, если соответственные углы у них равны.)
Равенство соответственных углов вытекает из свойства 4. Действительно, соответственные стороны исходного треугольника и его образа попарно параллельны, а это приводит к равенству углов.
 |
Осталось доказать, что коэффициент подобия равен модулю коэффициента гомотетии. Рассмотрим чертеж на рисунке 3. Из определения гомотетии следует, что

Из этого, по свойству пропорциональных отрезков, следует, что АВ параллельна А’В’, откуда вытекает, что треугольники М0АВ и М0А’В’ подобны, так как у них пропорциональны длины сторон, прилежащих к общему (или вертикальным, если k
Свойства, типы и примеры гомотетии
homotecia представляет собой геометрическое изменение в плоскости, где расстояния от фиксированной точки, называемой центром (O), умножаются на общий коэффициент. Таким образом, каждая точка P соответствует другой точке P ‘, являющейся произведением преобразования, и они выровнены с точкой O.
homotecia
Чтобы гомотетия была выполнена, они должны соответствовать точка-точка и прямая-прямая, чтобы пары гомологичных точек были выровнены с третьей фиксированной точкой, которая является центром гомотетии..
Аналогично, пары линий, которые соединяют их, должны быть параллельными. Соотношение между такими сегментами является константой, называемой коэффициентом гомотетии (k); таким образом, что гомотетия может быть определена как:
Чтобы сделать этот тип преобразования, вы начинаете с выбора произвольной точки, которая будет центром гомотетии..
С этой точки отрезки линий рисуются для каждой вершины фигуры, которая должна быть преобразована. Масштаб, в котором выполняется воспроизведение нового рисунка, определяется по причине гомотетии (k)..
свойства
Одним из основных свойств гомотетии является то, что по причине гомотетии (k) все гомотетические фигуры схожи. Среди других выдающихся свойств являются следующие:
— Линии, проходящие через центр, трансформируются (они двойные), но точки, составляющие его, не являются двойными.
— Прямые, которые не проходят через центр, превращаются в параллельные линии; таким образом, углы гомотетии остаются неизменными.
— Образ сегмента с помощью гомотетии центра O и отношения k представляет собой отрезок, параллельный этому, и имеет k-кратную длину. Например, как видно на следующем изображении, сегмент AB с помощью гомотетики приведет к другому сегменту A’B ‘, так что AB будет параллельным A’B’, а k будет:
С другой стороны, гомотетия варьируется в зависимости от значения ее отношения (k), и могут возникнуть следующие случаи:
— Если константа k = 1, все точки фиксированы, потому что они трансформируются. Таким образом, гомотетическая фигура совпадает с оригиналом и преобразование будет называться тождественной функцией.
— Если k ≠ 1, единственной фиксированной точкой будет центр гомотетии (O).
— Если k> 1, размер преобразованного рисунка будет больше размера исходного.
— Да 0 0; то есть гомотетические точки находятся на одной стороне относительно центра:
Коэффициент пропорциональности или отношения сходства между прямыми гомотетическими фигурами всегда будет положительным.
Преобразование фигур. Обратное преобразование. Определение и свойства гомотетии.
Описание презентации по отдельным слайдам:
Тема урока: Преобразование фигур. Обратное преобразование. Определение и свойства гомотетии. Учитель математики NIS ФМН г. Актобе Елешова Газиза Едиловна
На этом уроке вы узнаете, что такое гомотетия, познакомитесь: с терминами гомотетии; со свойствами гомотетии; научитесь применять свойства гомотетии при решении задач.
Задание Сейчас откроется таблица с терминами по теме «Гомотетия». Постарайтесь запомнить их за 30 секунд. Через 30 секунд таблица закроется.
Терминология на русском, казахском и английском языках Русский Қазақ English Подобие Ұқсастық Similar Гомотетия Гомотетия Enlargement Коэффициентподобия Ұқсастықкоэффициенті Scalefactor Центр Центр Centre Образ Бейне Image Фигура Фигура Shape
«Восстановите невидимое» Запишите термины, которые вы запомнили Русский Қазақ тілінде English Подобие Ұқсастық Similar Гомотетия Гомотетия Enlargement Коэффициентподобия Ұқсастықкоэффициентті Scalefactor Центр Центр Centre Образ Бейне Image Фигура Фигура Shape
Даурен стоит на набережной реки Сазды. На противоположном берегу идет Олжас. Даурен отчетливо видит его перемещение. Может ли он, стоя на одном месте, определить, хотя бы приблизительно, расстояние от себя до Олжаса? Условие: у Даурена нет никаких инструментов.
Гомотетия – одно из важнейших преобразований подобия. Это преобразование, в котором получаются подобные фигуры (фигуры, у которых соответствующие углы равны и стороны пропорциональны).
Подобие фигур Преобразование плоскости, при котором расстояния между точками умножаются на одно и то же положительное число, называется подобием. Само это число называется коэффициентом подобия. Две фигуры F и F’ называются подобными, если одна из них переводится в другую подобием.
Свойства подобия Свойство 1. Подобие переводит отрезки в отрезки, лучи в лучи и прямые в прямые. Свойство 2. Подобие сохраняет величины углов.
В отличие от гомотетии, геометрические преобразования — центральная симметрия, осевая симметрия, поворот, параллельный перенос являются движениями, т.к. в них фигура отображается в фигуру, равную данной.
Если фигура F преобразуется в результате гомотетии в фигуру F1, то фигуры F и F1 называются гомотетичными.
Свойства гомотетии с коэффициентом k. Прямая переходит в параллельную прямую. Угол переходит в равный ему угол. Отрезок переходит в отрезок. Длины всех отрезков изменяются в k раз.
Гомотетичные окружности Всякая гомотетия отображает окружность на окружность, так как при гомотетии все расстояния умножаются на одно и то же число – модуль коэффициента гомотетии.
Чтобы гомотетия была определена, должен быть задан центр гомотетии и коэффициент. Это можно записать так: гомотетия (О;k).
F F1 Пусть F – данная фигура, О – центр гомотетии. Проведем через точку А фигуры F луч ОА и отложим на нем отрезок ОА1, равный kОА. Так строится фигура, гомотетичная данной, с центром гомотетии О.
На рисунке из фигуры F можно получить F1 гомотетией (О;2)
Из фигуры F можно получить F1 гомотетией (О;-2)
Центр гомотетии может находиться и внутри фигуры. Треугольник A1B1C1 из треугольника ABC получен гомотетией
Гомотетия (О;−1) — это центральная симметрия или поворот на 180 градусов, в данном случае фигуры одинаковые.
Из определения гомотетии следует, что при k = 1 гомотетия является тождественным преобразованием. При k = –1 гомотетия становится центральной симметрией. Две гомотетии с центром в O и коэффициентами k и 1/k являются взаимно обратными. Это означает, что если одна из них переводит точку A в точку A1, то другая переводит A1 в A.
Гомотетичные фигуры подобны, но подобные фигуры не всегда гомотетичны (в гомотетии важно расположение фигур).
Практическое применение гомотетии Гомотетия чаще всего используется в задачах на нахождение ГМТ С помощью гомотетии можно строить подобные фигуры С помощью гомотетии можно находить отношение отрезков, площадей, объемов.
Для гомотетичных фигур F и F1 в силе формулы отношения периметров и площадей подобных фигур
Даурен стоит на набережной реки Сазды. На противоположном берегу идет Олжас. Даурен отчетливо видит его перемещение. Может ли он, стоя на одном месте, определить, хотя бы приблизительно, расстояние от себя до Олжаса? Условие: у Даурена нет никаких инструментов.
BМ-длина вытянутой руки Даурена, AB- расстояние между зрачками его глаз, CD измерено шагами Олжаса (шаг можно принять в среднем равным 3/4 м). Следовательно, неизвестное расстояние от Даурена до Олжаса на противоположном берегу реки Значит,
Если, например, расстояние между зрачками глаз у Даурена 6 см, длина от конца вытянутой руки до глаз 60 см, а Олжас сделал от А до В, скажем 14 шагов, то расстояние между ними
Задание для самостоятельного решения
Выполните задания на сайте www.bilimland.kz
Задание: Заполните пропуски
Задание: Заполните пропуски. Это две концентрических окружности. Одна окружность является проекцией другой, полученная с помощью гомотетии с центром в одних и тех же
Большая окружность является проекцией окружности, полученной с помощью гомотетии с коэффициентом равным отношению радиуса окружности к радиусу окружности
Проверка ответов Одна окружность является проекцией другой, полученной с помощью гомотетии с центром в одних и тех же центрах окружностей
Большая окружность является проекцией окружности, полученной с помощью гомотетии с коэффициентом равным отношению радиуса окружности к радиусу окружности большей меньшей
Как можно построить фигуру, гомотетичную данной на клетчатом листе?
Enlarge A using the given scale factor and centre of enlargement: k=2, centre (0,0) to obtain B k=3, centre (0,4) to obtain C A
(iii) Scale factor 4, centre (6,5) to obtain D (iv) Scale factor 5, centre (6,3) to obtain E A
Проверь себя A B C D E
(-1,1) A B Eg enlarge A with scale factor 2 about (5,5) to obtain B Multiply the number of horizontal and vertical squares from (5,5) to each corner by the scale factor
A B C D E Проверь себя
Построить треугольник, гомотетичный данному, взяв за центр гомотетии точку А и k = 2.
( А) Фигуры В и A гомотетичные. Найдите координаты центра гомотетии и коэффициент гомотетии. (Б) Чему равно отношение площади фигуры А и В?
(С)Фигуры С и A гомотетичные. Найдите координаты центра гомотетии и коэффициент гомотетии.
ВОПРОСЫ НА ЗАСЫПКУ
Существуют ли прямые, которые переводятся гомотетией сами в себя?
Ответ: Да, прямые, проходящие через центр гомотетии.
Даны точки A, B и гомотетичные им точки A´, B´ соответственно. Можно ли найти центр данной гомотетии?
Ответ: Да. Это точка пересечения прямых AA’ и BB’.
Как расположены две окружности друг относительно друга, если их центром гомотетии является центр одной из окружностей?
Ответ: Имеют общий центр
Как расположены две окружности друг относительно друга, если их центром гомотетии является точка, принадлежащая одной из данных окружностей?
Ответ: Касаются внутренним образом.
Задача Коэффициент подобия равен 3, точка О является центром гомотетии. Найти значение х. P Q O
Существуют ли механизмы, инструменты, которые помогают построить фигуру, гомотетичную данной, помимо тех, которые мы уже рассмотрели?
Задача на построение: Впишите в данный треугольник квадрат, у которого две вершины лежат на одной стороне, а две другие вершины — на двух других сторонах.
Дано: OMP Построить: квадрат ABCD, A OM, B MP, C OP, D OP Решение: 1) Строим квадрат A1B1C1D1: A1 OM, C1 OP, D1 OP 2) OB1 ∩ MP = B 3) BC OP, BA || OP, AD OP 4) ABCD – искомый квадрат O D1 C1 D C B M A A1 B1 O D1 C1 D C P B M A A1 B1
Задача на доказательство:
Отрезки АВ и СD расположены гомотетично относительно точки О, следовательно: Отсюда получаем: Значит, Ответ: Длина обрыва 2002,5 футов Решение:
Жилой дом. На фотографии виден жилой дом, у которого крыша имеет форму пирамиды. Ниже изображена сделанная учащимся математическая модель крыши дома и указаны длины некоторых отрезков.
Что объединяет эти рисунки?
Ответ Эти фигуры объединяет гомотетия.
Поиграем в kahoot.it
Домашнее задание «Клад сумасшедшего математика»
«Если идти по дороге, гомотетичной тайной тропе относительно вулкана и дойти до маяка, а затем перейти в точку симметричную маяку относительно большой пальмы, то рядом, у подножия большой подобной горы зарыт клад». Зная, что тайная тропа обозначена отрезком АВ, найти в какой точке зарыт клад.
Сегодня я узнал… Было интересно… Я понял, что… Теперь я могу… Я научился… У меня получилось… Я попробую…. Меня удивило… Мне захотелось… Сегодня я могу оценить свою работу на «___». Рефлексия
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-502297
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Российские юниоры завоевали 6 медалей на Международной научной олимпиаде
Время чтения: 2 минуты
В Госдуме проверят содержание учебников русского языка как иностранного
Время чтения: 2 минуты
При детском омбудсмене в России создадут платформу для взаимодействия с родителями
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Большинство родителей в России удовлетворены качеством образования в детсадах
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.