Как построить тетраэдр по клеткам
Тетраэдр
Тетраэдр имеет следующие характеристики:
Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.
Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.
Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.
Математические характеристики тетраэдра
Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы тетраэдра определяется по формуле:
Сфера может быть вписана внутрь тетраэдра.
Радиус вписанной сферы тетраэдра определяется по формуле:
Площадь поверхности тетраэдра
Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:
Объем тетраэдра определяется по следующей формуле:
Высота тетраэдра определяется по следующей формуле:
Расстояние до центра основания тетраэдра определяется по формуле:
Вариант развертки
Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.
Заметим, что это не единственный вариант развертки.
Видео. Тетраэдр из набора «Волшебные грани»
Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора «Волшебные грани».
Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал Оригами)
вращение готового многогранника:
Видео. Вращение всех правильных многогранников
Урок «Тэтраэдр»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Добрый день! Мы продолжаем с вами изучать тему: «Параллельность прямых и плоскостей».
Я думаю, уже понятно, что сегодня речь пойдет о многогранниках- поверхностях геометрических тел, составленных из многоугольников.
А именно о тетраэдре.
Проводить изучение многогранников будем по плану:
1. определение тетраэдра
2. элементы тетраэдра
3. развертка тетраэдра
4. изображение на плоскости
1. построим треугольник АBC
2. точка D, не лежащая в плоскости этого треугольника
3. соединяем точку D отрезками с вершинами треугольника ABC. Получим треугольники DAB, DBC и DCA.
Определение: Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA называется тетраэдром.
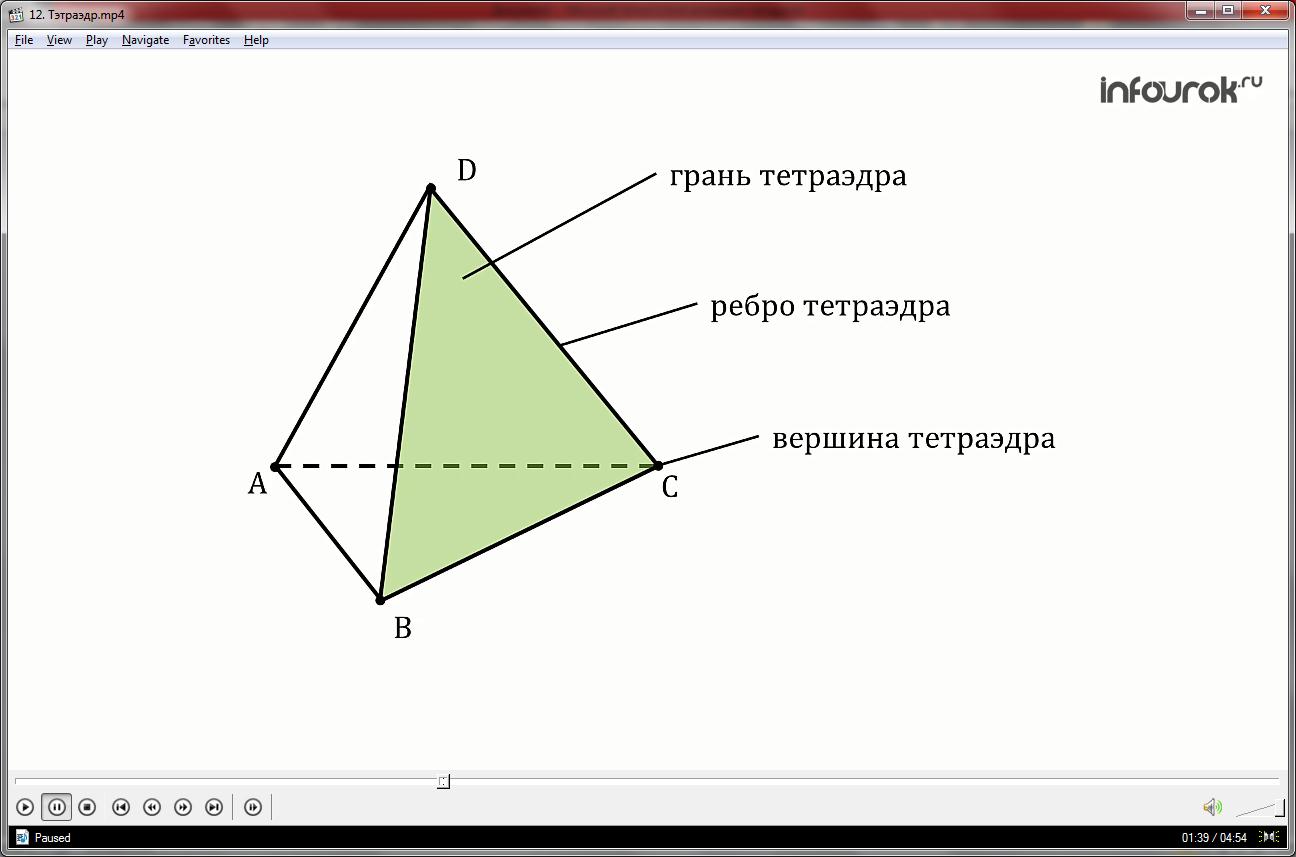
Треугольники, из которых состоит тетраэдр, называются гранями, их стороны ребрами, а вершины – вершинами тетраэдра.
Сколько граней, ребер и вершин имеет тетраэдр?
Тетраэдр имеет четыре грани, шесть ребер и четыре вершины
Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.
На рисунке противоположными являются ребра AD и BC, BD и AC, CD и AB
Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие – боковыми гранями.
Для изготовления тетраэдра из бумаги вам потребуется следующая развертка,
ее нужно перенести на плотную бумагу, вырезать, согнуть по пунктирным линиям и склеить.
На плоскости тетраэдр изображается
В виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.
На первом рисунке AC- невидимое ребро,
на втором – EK, LK и KF.
Решим несколько типовых задач на тетраэдр:
Найти площадь развертки правильного тетраэдра с ребром 5 см.
Решение. Начертим развертку тетраэдра
(на экране появляется развертка тетраэдра )
Данный тетраэдр состоит из четырех равносторонних треугольников, следовательно, площадь развертки правильного тетраэдра равна площади полной поверхности тетраэдра или площади четырех правильных треугольников.
Площадь правильного треугольника ищем по формуле:
Тогда получаем площадь тетраэдра равна:
Подставим в формулу длину ребра а=5 см,
Ответ: Площадь развертки правильного тетраэдра
Постройте сечение тетраэдра плоскостью проходящей через точки M, N и K.
а) Действительно, соединим точки M и N (принадлежат грани ADC), точки M и K(принадлежат грани ADB), точки N и K (грани DBC). Сечением тетраэдра является треугольник MKN.
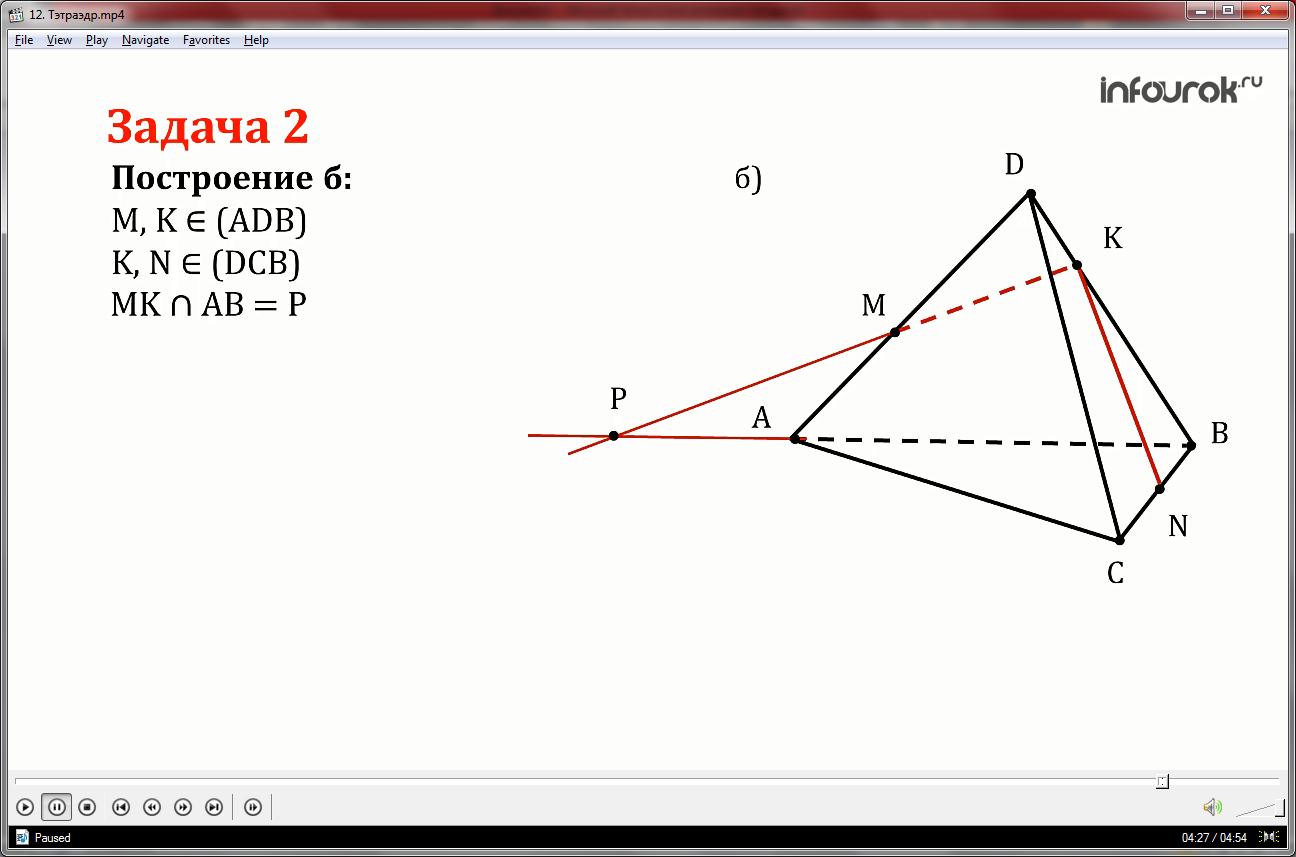
б) Соединим точки M и K (принадлежат грани ADB), точки K и N(принадлежат грани DCB), далее прямые MK и AB продолжить до пересечения и поставить точку P. Прямая PN и точка T лежат в одной плоскости АВС и теперь можно построить пересечение прямой МК с каждой гранью. В результате получается четырехугольник MKNT, который является искомым сечением.
© 2021 Проект «Уроки математики»
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.
Тетраэдр из картона. Схема, как сделать поэтапно, шаблон
Тетраэдр, сделанный из бумаги или картона можно использовать в качестве модели, объясняя школьнику особенности этой фигуры в геометрии. Ещё самодельные объёмные фигуры можно использовать для декора комнаты или рабочего стола. Чтобы научиться делать тетраэдр своими руками, нужно прочесть несколько поэтапных инструкций по изготовления фигур из разных материалов.
Особенности фигуры, сколько граней и углов у тетраэдра
Тетраэдр – это объёмная геометрическая фигура треугольной формы. Она выглядит как пирамида. У тетраэдра 6 ребер, 4 вершины и 4 грани. Размеры и формы граней зависят от вида геометрической фигуры.
Какими бывают тетраэдры:
| Равногранный | Грани равны между собой. |
| Ортоцентрический | Высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке. |
| Прямоугольный | Ребра, прилежащие к 1 из вершин, перпендикулярны между собой. |
| Инцентрический | Отрезки фигуры соединяют вершины с центральными точками окружностей, вписанных в противоположные грани и пересекающихся в 1 точке. |
Самый простой вид фигуры называется «правильный тетраэдр». Его грани – это односторонние треугольники. Собрать правильный тетраэдр из бумаги или картона намного проще, чем другие виды этой фигуры. Далее в статье можно рассмотреть примеры построения развёрток, а также прочесть инструкцию по склеиванию объёмной фигуры.
Что понадобиться, чтобы сделать тетраэдр своими руками
Перечень материалов и инструментов, необходимых для создания бумажного, либо картонного тетраэдра:
Желательно, чтобы бумага, на которой будет построен чертеж, была плотной. Подойдут листы для черчения, акварельная бумага или листы из альбома. Можно использовать бумагу для принтера, плотностью не менее 80 г/кв. м. Более тонкий материал будет плохо держать форму, а также рваться и мяться в процессе склеивания фигуры.
Как сделать из бумаги А4
Изготовление тетраэдра проходит в 5 этапов:
Для склеивания бумажных конструкций можно использовать обыкновенный канцелярский клей или ПВА. Для фигур, сделанных из более плотных материалов, желательно использовать клей «Момент» или качественный двухсторонний скотч без мягкой прослойки между клеевыми лентами.
Расчет размера
Размер будущей фигуры зависит вида развертки. Грани можно расположить по кругу. В таком случае фигура получиться небольшой. Высота такого тетраэдра будет около 6 см. Если начертить горизонтальную развёртку, где грани будут расположены в таком порядке, что образуют фигуру в виде параллелограмма. В таком случае, можно получить более крупную фигуру.
Оптимальная длина ребра тетраэдра, начерченного в горизонтальной развертке на листе формата А4 – 10 см.
В итоге получится параллелограмм с диагональю равной 26,6 см. Размер листа формата А4 равен 21×29,7 см. Диагональ листа равна 36,4 см. Поэтому развертка с диагональю 26,6 см идеально поместиться на бумаге А4, и еще останется свободнее место, чтобы начертить полосы для склеивания фигуры.
Подготовка шаблона из картона
Из картона можно сделать шаблон 1 грани тетраэдра, чтобы потом было проще построить развертку.
Как сделать заготовку поэтапно:
Ножницами аккуратно вырезать шаблон.
Построение развертки, чертежи
Как начертить круговую развертку тетраэдра с помощью картонного шаблона:
Ластиком удалить лишние линии.

Как начертить горизонтальную развертку тетраэдра, не используя картонный шаблон:
Работа с готовой формой, склеивание
Склеить фигуру по вырезанной развертке несложно.
Порядок действий:
Располагать «ушки» для крепления нужно изнутри. Чтобы детали хорошо склеились, необходимо придерживать пальцами места соединений в течение 10-15 сек.
Большой тетраэдр из картона
Тетраэдр из картона (сделать поэтапно можно по инструкции, представленной далее в статье) получится крепким и будет хорошо держать форму. Размер объёмной фигуры зависит от вида картона.
Какой картон можно использовать для работы:
Не цветной картон после сборки тетраэдра можно покрасить или обклеить бумагой с узорами. Если на грани небольшой фигуры наклеить календарные листы или фотографии, можно получить необычное украшение для рабочего стола.
Особенности работы с жестким картоном
Тетраэдр из картона (сделать поэтапно развертку можно, не используя шаблоны) изготавливают следуя этим правилам:
Удобнее всего работать с двухслойным гофрированным картоном. Его можно вырезать из большой коробки, в которой перевозят бытовую технику. С картоном, сложенным в 3 и более слоя, работать будет намного сложнее. Такой материал плохо гнется и тяжело склеивается.
Подготовка и вырезание шаблона
Тетраэдр из картона (сделать поэтапно можно за 1 ч) можно изготовить, используя любой вид развертки. В этом мастер-классе описан процесс составления круговой развертки, без использования шаблона.
Порядок действий:
В итоге должна получиться развертка из 4 треугольных граней. Остается добавить «ушки» для крепления. Чем шире будут «ушки», тем надежнее будет соединение. Минимальная ширина этих полосок – 5 см.
Где должны располагаться «ушки»:
Вырезать развертку канцелярским ножом.
Соединение граней
Как соединить грани фигуры:
Дождаться полного высыхания клея. Если остались излишки (застывшие капли или паутинки), их можно аккуратно срезать канцлерским ножом.
Научиться делать тетраэдр из бумаги или картона помогут инструкции, где все действия расписаны поэтапно. Главное, составить точный чертеж, а затем аккуратно вырезать развертку, используя подходящие инструменты.
Как начертить тетраэдр по клеточкам
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Добрый день! Мы продолжаем с вами изучать тему: «Параллельность прямых и плоскостей».
Я думаю, уже понятно, что сегодня речь пойдет о многогранниках- поверхностях геометрических тел, составленных из многоугольников.
А именно о тетраэдре.
Проводить изучение многогранников будем по плану:
1. определение тетраэдра
2. элементы тетраэдра
3. развертка тетраэдра
4. изображение на плоскости
1. построим треугольник АBC
2. точка D, не лежащая в плоскости этого треугольника
3. соединяем точку D отрезками с вершинами треугольника ABC. Получим треугольники DAB, DBC и DCA.
Определение: Поверхность составленная из четырех треугольников АBC, DAB, DBC и DCA называется тетраэдром.
Треугольники, из которых состоит тетраэдр, называются гранями, их стороны ребрами, а вершины – вершинами тетраэдра.
Сколько граней, ребер и вершин имеет тетраэдр?
Тетраэдр имеет четыре грани, шесть ребер и четыре вершины
Два ребра тетраэдра, не имеющие общих вершин, называются противоположными.
На рисунке противоположными являются ребра AD и BC, BD и AC, CD и AB
Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие – боковыми гранями.
Для изготовления тетраэдра из бумаги вам потребуется следующая развертка,
ее нужно перенести на плотную бумагу, вырезать, согнуть по пунктирным линиям и склеить.
На плоскости тетраэдр изображается
В виде выпуклого или невыпуклого четырехугольника с диагоналями. При этом штриховыми линиями изображаются невидимые ребра.
На первом рисунке AC- невидимое ребро,
на втором – EK, LK и KF.
Решим несколько типовых задач на тетраэдр:
Найти площадь развертки правильного тетраэдра с ребром 5 см.
Решение. Начертим развертку тетраэдра
(на экране появляется развертка тетраэдра )
Данный тетраэдр состоит из четырех равносторонних треугольников, следовательно, площадь развертки правильного тетраэдра равна площади полной поверхности тетраэдра или площади четырех правильных треугольников.
Площадь правильного треугольника ищем по формуле:
Тогда получаем площадь тетраэдра равна:
Подставим в формулу длину ребра а=5 см,
Ответ: Площадь развертки правильного тетраэдра
Постройте сечение тетраэдра плоскостью проходящей через точки M, N и K.
а) Действительно, соединим точки M и N (принадлежат грани ADC), точки M и K(принадлежат грани ADB), точки N и K (грани DBC). Сечением тетраэдра является треугольник MKN.
б) Соединим точки M и K (принадлежат грани ADB), точки K и N(принадлежат грани DCB), далее прямые MK и AB продолжить до пересечения и поставить точку P. Прямая PN и точка T лежат в одной плоскости АВС и теперь можно построить пересечение прямой МК с каждой гранью. В результате получается четырехугольник MKNT, который является искомым сечением.
© 2019 Проект «Уроки математики»
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы рассмотрим тетраэдр и его элементы (ребро тетраэдра, поверхность, грани, вершины). И решим несколько задач на построение сечений в тетраэдре, используя общий метод для построения сечений.
Тема: Параллельность прямых и плоскостей
Урок: Тетраэдр. Задачи на построение сечений в тетраэдре
Тетраэдр и его элементы
Как построить тетраэдр? Возьмем произвольный треугольник АВС. Произвольную точку D, не лежащую в плоскости этого треугольника. Получим 4 треугольника. Поверхность, образованная этими 4 треугольниками, и называется тетраэдром (Рис. 1.). Внутренние точки, ограниченные этой поверхностью, также входят в состав тетраэдра.
Рис. 1. Тетраэдр АВСD
Замечание: можно принять плоскость АВС за основание тетраэдра, и тогда точка D является вершиной тетраэдра. Каждое ребро тетраэдра является пересечением двух плоскостей. Например, ребро АВ – это пересечение плоскостей АВD и АВС. Каждая вершина тетраэдра – это пересечение трех плоскостей. Вершина А лежит в плоскостях АВС, АВD, АDС. Точка А – это пересечение трех означенных плоскостей. Этот факт записывается следующим образом: А = АВС ∩ АВD ∩ АСD.
Тетраэдр определение
Итак, тетраэдр — это поверхность, образованная четырмя треугольниками.
Ребро тетраэдра — линия перечесения двух плоскостей тетраэдра.
Задача 1 на построение тетраэдра
Составьте из 6 спичек 4 равных треугольника. На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек – это его ребра, четыре грани тетраэдра и будут четырьмя равными треугольниками. Задача решена.
Задача 2 Построить сечение тетраэдра плоскостью
Дан тетраэдр АВСD. Точка M принадлежит ребру тетраэдра АВ, точка N принадлежит ребру тетраэдра ВD и точка Р принадлежит ребру DС (Рис. 2.). Постройте сечение тетраэдра плоскостью MNP.
Рис. 2. Рисунок к задаче 2 — Построить сечение тетраэдра плоскостью
Решение:
Рассмотрим грань тетраэдра DВС. В этой грани точки N и P принадлежат грани DВС, а значит, и тетраэдру. Но по условию точки N, P принадлежат секущей плоскости. Значит, NP – это линия пересечения двух плоскостей: плоскости грани DВС и секущей плоскости. Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости DВС. Найдем точку пересечения прямых NP и ВС. Обозначим ее Е (Рис. 3.).
Рис. 3. Рисунок к задаче 2. Нахождение точки Е
Точка Е принадлежит плоскости сечения MNP, так как она лежит на прямой NР, а прямая NР целиком лежит в плоскости сечения MNP.
Также точка Е лежит в плоскости АВС, потому что она лежит на прямой ВС из плоскости АВС.
Получаем, что ЕМ – линия пересечения плоскостей АВС и MNP, так как точки Е и М лежат одновременно в двух плоскостях — АВС и MNP. Соединим точки М и Е, и продолжим прямую ЕМ до пересечения с прямой АС. Точку пересечения прямых ЕМ и АС обозначим Q.
Итак, в этом случае NPQМ — искомое сечение.
Рис. 4. Рисунок к задаче 2.Решение задачи 2
Рассмотрим теперь случай, когда NP параллельна BC. Если прямая NP параллельна какой-нибудь прямой, например, прямой ВС из плоскости АВС, то прямая NP параллельна всей плоскости АВС.
Искомая плоскость сечения проходит через прямую NP, параллельную плоскости АВС, и пересекает плоскость по прямой МQ. Значит, линия пересечения МQ параллельна прямой NP. Получаем, NPQМ — искомое сечение.
Задача 3 Построить сечение тетраэдра плоскостью
Точка М лежит на боковой грани АDВ тетраэдра АВСD. Постройте сечение тетраэдра плоскостью, которое проходит через точку М параллельно основанию АВС.
Рис. 5. Рисунок к задаче 3 Построить сечение тетраэдра плоскостью
Решение:
Секущая плоскость φ параллельна плоскости АВС по условию, значит, эта плоскость φ параллельна прямым АВ, АС, ВС.
В плоскости АВD через точку М проведем прямую PQ параллельно АВ (рис. 5). Прямая PQ лежит в плоскости АВD. Аналогично в плоскости АСD через точку Р проведем прямую РR параллельно АС. Получили точку R. Две пересекающиеся прямые PQ и РR плоскости РQR соответственно параллельны двум пересекающимся прямым АВ и АС плоскости АВС, значит, плоскости АВС и РQR параллельны. РQR – искомое сечение. Задача решена.
Задача 4
Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС (Рис. 6.). Построить точку пересечения прямой NM и плоскости АВС.
Рис. 6. Рисунок к задаче 4
Решение:
Для решения построим вспомогательную плоскость DМN. Пусть прямая DМ пересекает прямую АВ в точке К (Рис. 7.). Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.
Рис. 7. Рисунок к задаче 4. Решение задачи 4
Задача 5 Построить сечение тетраэдра плоскостью
Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС (Рис. 8.). Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.
Рис. 8. Рисунок к задаче 5 Построить сечение тетраэдра плоскостью
Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС. В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.
Рис. 9. Рисунок к задаче 5. Нахождение точки К
Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р1 и Р2. Соединяем Р1 и М и на продолжении получаем точку М1. Соединяем точку Р2 и N. В результате получаем искомое сечение Р1Р2NМ1. Задача в первом случае решена.
Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС. Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р1Р2, тогда прямая Р1Р2 параллельна данной прямой MN (Рис. 10.).
Рис. 10. Рисунок к задаче 5. Искомое сечение
Итоги урока по теме «Тетраэдр», «Ребро тетраэдра», «Грани тетраэдра», «Поверхность тетраэдра», «Вершины тетраэдра»
Итак, мы рассмотрели тетраэдр, решили некоторые типовые задачи на тетраэдр. На следующем уроке мы рассмотрим параллелепипед.
Список рекомендованной литературы по теме «Тетраэдр»
1. И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни)
2. Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений
3. Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М. : Дрофа, 008. – 233 с. :ил. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики
Дополнительные веб-ресурсы
1. Сечения тетраэдра (Источник).
2. Как построить сечение тетраэдра. Математика (Источник).
3. Фестиваль педагогических идей (Источник).
Сделай дома задачи по теме «Тетраэдр», как находить ребро тетраэдра, грани тетраэдра, вершины и поверхность тетраэдра
1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.: ил. Задания 18, 19, 20 стр. 50
2. Точка Е середина ребра МА тетраэдра МАВС. Постройте сечение тетраэдра плоскостью, проходящей через точки В, С и Е.
3. В тетраэдре МАВС точка М принадлежит грани АМВ, точка Р – грани ВМС, точка К – ребру АС. Постройте сечение тетраэдра плоскостью, проходящей через точки М, Р, К.
4. Какие фигуры могут получиться в результате пересечения плоскостью тетраэдра?
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
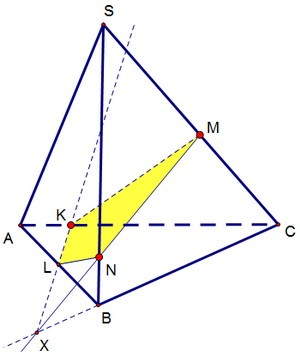
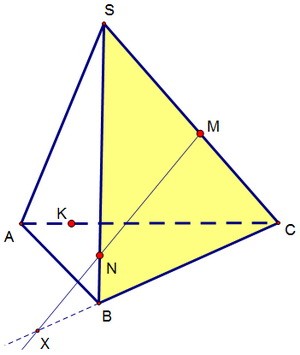
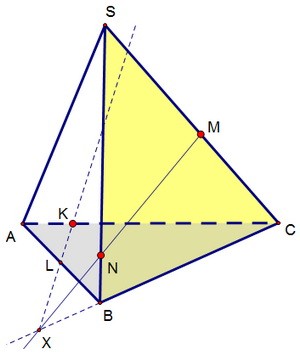
14(C2). Сечение тетраэдра по трём точкам
Построить сечение тетраэдра SАВС через три точки K, M, N, лежащие соответственно на рёбрах АС, SC и SB. 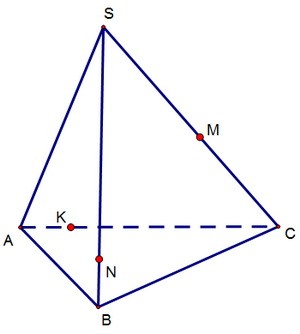
Автор: Ольга Себедаш Просмотров: 64926
Комментарии к этой задаче:
Комментарий добавил(а): Виктория
Дата: 2014-11-23
Спасибо, очень помогли, построила в два счета
Комментарий добавил(а):
Дата: 2018-12-07