Как построить тени в аксонометрии

06.12.202328.06.2023 admin 0 Comments

Построение теней в аксонометрии

В аксонометрических проекциях так же различают тени собственные и тени падающие.

Тень от точки. Перед построением тени от точки в аксонометрии необходимо задаться направлением светового луча S в пространстве и вторичной его проекции S₁.

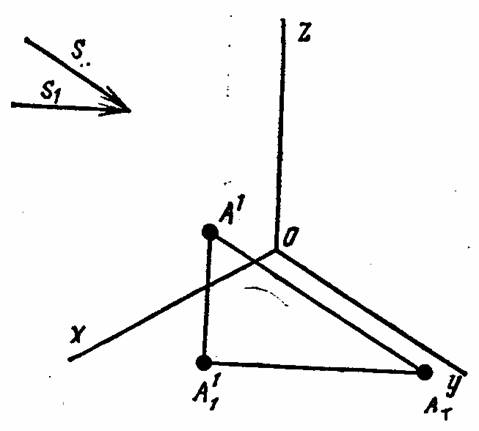
Для построения тени через аксонометрическую проекцию Т точки А проводим луч параллельно заданному S, а через вторичную проекцию А´₁ проводим прямую, параллельную вторичной проекции луча S₁. Точка пересечения лучей будет тенью от точки А (рисунок 11.35).

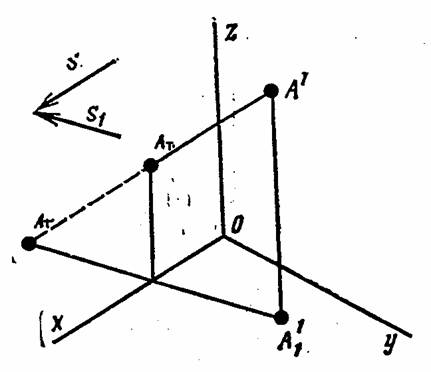
В зависимости от расположения точки в пространстве тень может падать на горизонтальную плоскость (рисунок 11.35) или на вертикальную (рисунок 11.36), фронтальную или профильную.

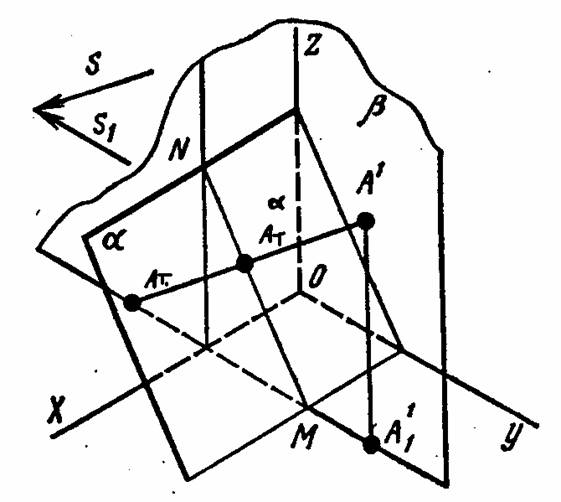
Если тень от точки А´ будет падать на наклонную плоскость (рисунок 11.37), например на плоскость α, то тень найдется в результате построения точки пересечения луча S с плоскостью α.

Для этого следует: заключить луч S в горизонтально – проецирующую плоскость β (S‹β);

найти линию пересечения МN плоскостей α и β, тогда точки пересечения луча S с линией пересечения МN даст тень от точки А на плоскость α.

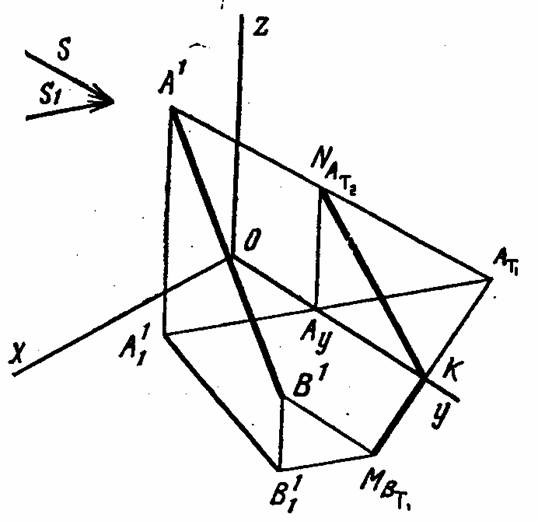
Тень от отрезка прямой линии. Рассмотрим построение тени прямой общего положения АВ. Зададимся аксонометрическими осями Х,Y, Z, прямой А´/В´ общего положения с ее вторичной проекцией А´₁/B´₁, а так же направлением светового луча S и его вторичной проекцией S₁ (рисунок 11.38).

Для нахождения падающей тени проводим через отрезок прямой лучевую плоскость и находим ее след на горизонтальной или на фронтальной плоскости проекции. Для этого через точки А 1 и В 1 проводим лучи и находим следы (тени) этих лучей А_Т1 и В_Т1. Из построения видно, что тень от точки В легла на горизонтальную плоскость, а тень от точки А легла за пределами вертикальной плоскости, и на пересечении с осью Y будем иметь точку перелома тени Т. Теперь найдем тень от точки А на вертикальной плоскости, для этого из точки А_Y восставим перпендикуляр до пересечения его с лучом, идущим из точки А. точка пересечения и будет тенью от точки А на профильной плоскости. Найдем точку соединяем с точкой перелома К.

В аксонометрических проекциях, так же как и в ортогональных проекциях, могут иметь место различные положения прямой в пространстве. Если прямая будет расположена ближе к горизонтальной плоскость то и тень от нее не упадет на горизонтальную плоскость, а при расположении отрезка ближе к фронтальной (вертикальной) плоскости вся тень упадет на фронтальную плоскость.

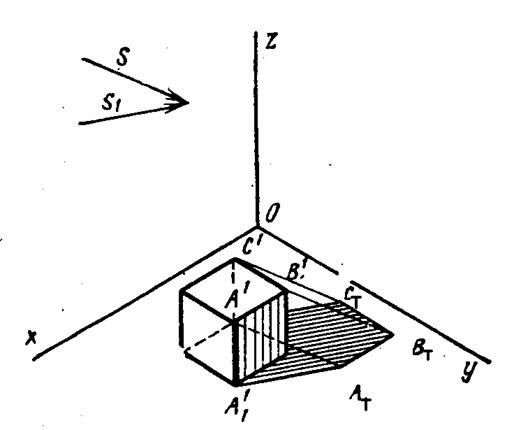
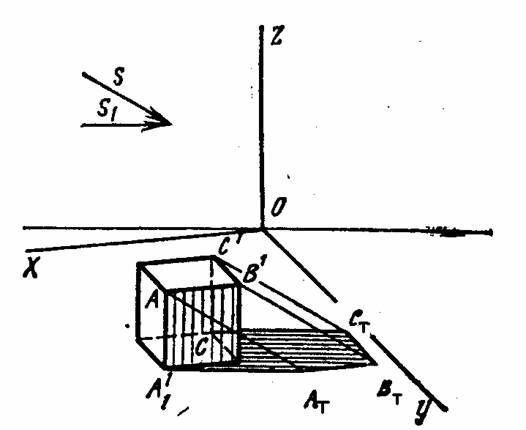
Тени от геометрических тел. От любого геометрического тела можно построит в той или иной аксонометрической проекции падающую тень, а на самом теле найти его собственную тень. На рисунке 11.39, 11.40 построены кубы в прямоугольной изометрии и диметрии, найдены падающие тени и показаны тени собственные.

Во всех видах аксонометрических проекциях техника построения теней одинакова. Вычерчиваем предмет, задаемся направлением луча S и его вторичной проекции S₁. Через каждую точку проводим лечи S, а через проекции точек предмета – проекции лучей S₁.

Пересечение луча S с проекцией луча S₁ даст тень от точки А в точке А_К. Найдя таким образом тени ряда точек, соединяем их между собой и с основанием, если предмет стоит на плоскости.

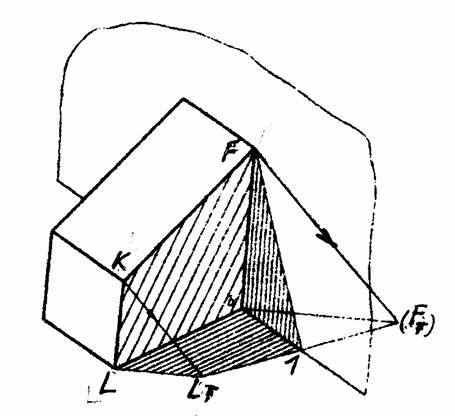
На рисунке 11.41 построена тень от пирамиды в четырех вариантах, т.е. освещение взято с разных сторон. Часто берут направление луча параллельно диагонали куба, как в метода ортогональных проекций. Для того чтобы построить тень от пирамиды, стоящей на горизонтальной плоскости, надо задаться направлением луча в пространстве и его проекцией на плоскости, причем направление луча можно выбрать в зависимости от желания показать в тени те или иные элементы предмета.

Так, на рисунке 11.41а тень падает слева, вторичная проекция луча параллельна оси проекции ОХ. На рисунке 11.41б предмет освещен сзади, вторичная проекция луча направлена в обратном направлении. На рисунке 11.41в предмет освещен с лева и сзади, а на рисунке 11.41г – слева направо.

Примеры построения теней на строительных объектах.

Рассмотрим подробнее построение теней отдельных элементов зданий.

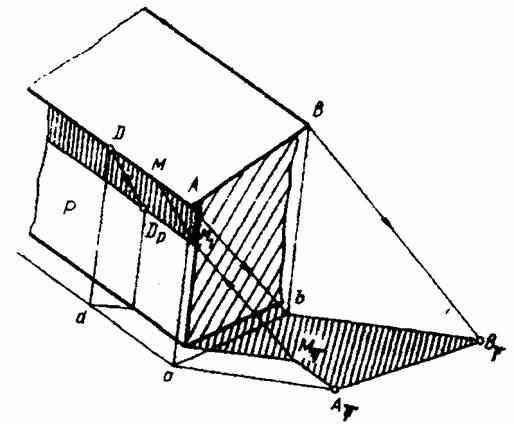
На рисунке 11.42 показано построение тени от карниза AD на плоскость стены Р. Тень карниза пройдет через точку D_P – тень от произвольной точки D на плоскость Р и будет параллельна карнизу, так как карниз параллелен плоскости Р. Эту же тень можно построить способом обратного луча. С этой целью из точки М_Т, в которой пересекаются тени, падающие на землю от карниза и от угла стены, проведен луч в обратном направлении до пересечения его в точке М₁ с углом стены. Тень от карниза по стене пройдет через точку М₁.

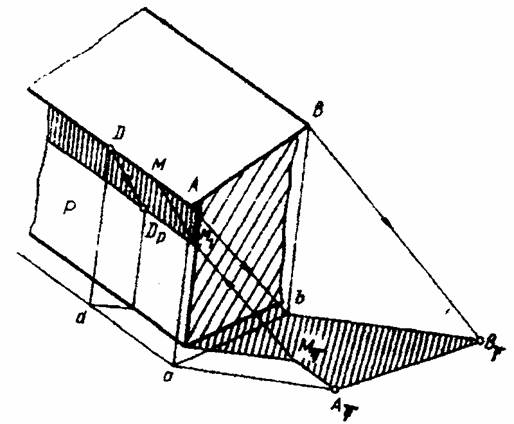
На рисунке 11.43 показано построение тени от цоколя и угла стены.

Контур собственной тени цоколя проходит через точки В, А и С, а на стене граница собственной тени – угол стены DE. Тень прямой АВ совпадает с проекцией луча, тень прямой АС проходит через тень А_Т параллельно АС. Тень от угла стены падает сначала на верхнюю плоскость (обрез) цоколя и параллельна проекции луча, а затем в точке F₁ «соскальзывает» с цоколя на землю и дальше идет через точку F_T по земле параллельно проекции луча.

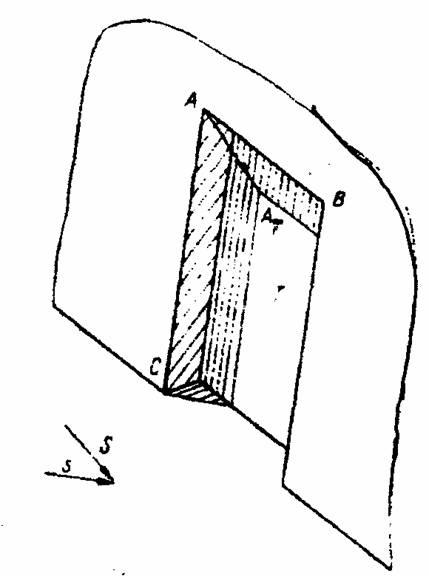
На рисунке 11.44 изображена дверная ниша.

Тени будут отбрасывать прямые АВ и АС. Эти тени будут параллельны указанным прямым и проходят через точку А_Т – тень от точки А, падающую на плоскость ниши Т.

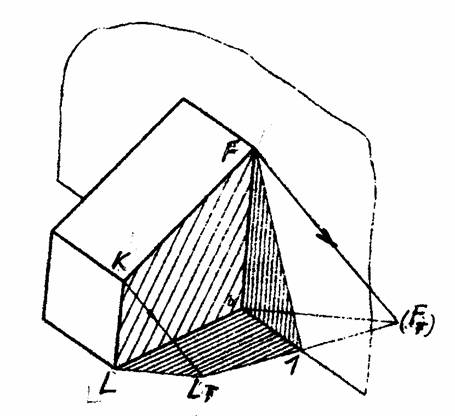
Контур собственной тени пристройки к стене, изображенной на рисунке 11.45 проходит через точки L, K и F.

Тень от прямой LK совпадает с проекцией луча. Тень от прямой KF по горизонтальной плоскости Н пойдет через точку К_Т и мнимую тень от точки F на Н – F_T. В действительности, тень от точки F совпадает с этой точкой, и, дойдя до стены, тень в точке 1 изломится и по стене пойдет в точку F, в которой прямая KF пересекает стену.

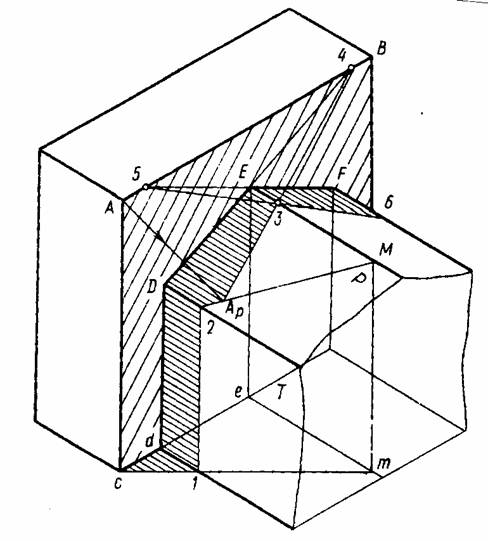
К торцевой стене здания (рисунок 11.46) примыкает пристройка призматической формы, контур собственной тени которой проходит через точки С, А и В.

Рассмотрим построение тени пристройки, падающей на здание. Тень прямой СА на участке С1 совпадает с проекцией луча света, на участке 1 – 2 параллельна СА, так как указанная прямая параллельна стене. Тень от точки А падает на передний скат крыши, эта тень А_Р расположена на прямой 2М, по которой пересекает крышу вспомогательная горизонтально-проецирующая плоскость, проведенная через луч света, проходящий через точку А. Тень от прямой АВ на передний скат крыши проходит через точку А_Р и точку 4, в которой прямая АВ пересекла бы плоскость Р, если ее продлить вправо вверх. Дойдя до конька крыши, в точке 3 тень изломится и пройдет по заднему скату крыши в точку 6. прямая 3 – 6 есть продолжение прямой 5 – 3. В точке 5 прямая АВ пересекла бы скат крыши, если его продлить влево вверх (тень от прямой на плоскость проходит через точку пересечения прямой с плоскостью).

Литература

ГЛАВА 12

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Построение теней в аксонометрии

Основные правила построения теней, изложенные применительно к ортогональным проекциям, остаются в силе и при построении теней в аксонометрических проекциях. Особенности – только в задании направления светового луча.

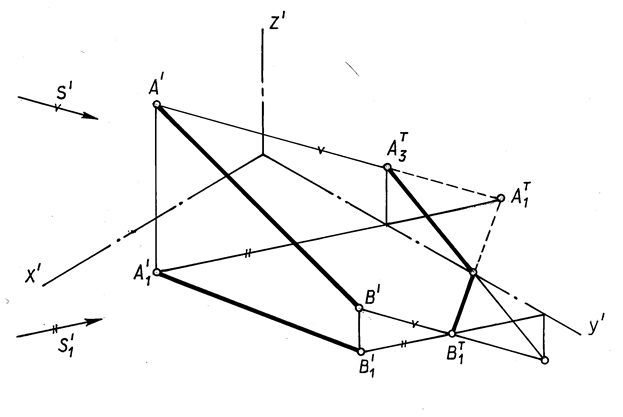
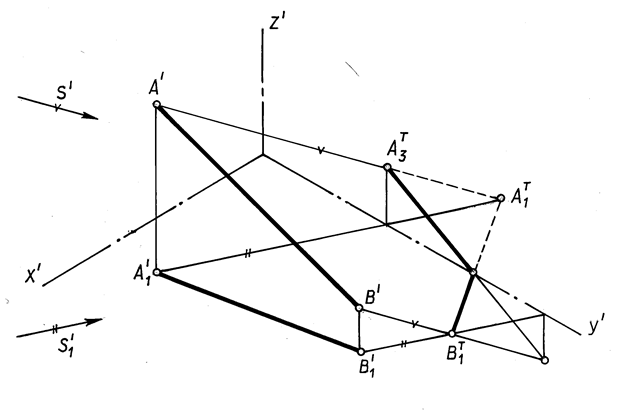
В аксонометрических проекциях направление лучей света может быть принято любым, но при этом нужно соблюдать условие правдоподобности освещения, а также помнить, что тень является средством выявления формы и придания чертежу наибольшей выразительности. Лучи не должны быть слишком пологими или слишком крутыми; лучшим углом наклона луча света к горизонту можно считать 30°…40°. Направление светового луча задаётся его аксонометрической S’ и вторичной S₁’ проекциями (рис.18.10).

Для построения тени точки В’ (рис. 18.10) через аксонометрическую проекцию В’ проводят аксонометрию луча параллельно заданному направлению S’, а через вторичную проекцию В₁’ проводим прямую, параллельную вторичной проекции луча S₁’. Точка пересечения луча с его вторичной проекцией и есть тень точки В.

В зависимости от расположения точки в пространстве тень может падать на горизонтальную плоскость. Так из построения тени точки А (рис. 18.10) видно, что тень от точки А легла на горизонтальную плоскость за пределами вертикальной профильной плоскости.

Для определения тени точки А₃ T точки А на профильной плоскости необходимо из точки пересечения вторичной проекции светового луча с

осью у’ провести вертикальную прямую до пересечения с аксонометрией луча, проходящего через точку А.

Для построения тени отрезка АВ в аксонометрии на рис. 18.10 использована мнимая тень (А₁ Т ) точки А.

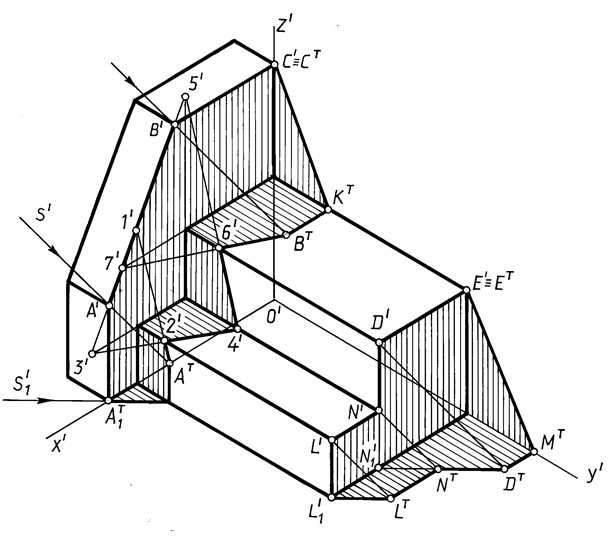
На рис. 18.11 построены тени от лестницы и тени от тумбы, имеющей форму усечённого параллелепипеда.

Отметим, что в аксонометрии тень от вертикального отрезка на горизонтальной плоскости совпадает с направлением вторичной проекции светового луча, а тень от любой прямой на плоскость, ей параллельную, параллельна самой прямой.

Построения тени от лестницы ясны из чертежа.

На рис.18.11 тени на лестнице от тумбы построены в следующем порядке:

1. Определена тень от вертикального отрезка А’А’₁.

2. Определена точка пересечения наклонной прямой А’В’ с вертикальной плоскостью первой ступени – точка 1’. Из точки А Т тень по вертикальной плоскости идёт в точку 1’ и заканчивается в точке 2’.

3. Продолжена наклонная прямая А’В’ до пересечения с горизонтальной плоскостью ступеньки и получена точка 3’. Соединив точки 2’ и 3’, получили тень от отрезка А’В’ на горизонтальной плоскости первой ступеньки, которая заканчивается в точке 4’.

На второй ступеньке тень от отрезка А’В’ строится аналогично. Выполненные построения ясны из чертежа.

4. Тень от горизонтального отрезка В’ С’ на горизонтальной плоскости параллельна самому отрезку, а на фасадной плоскости идёт в точку С Т (точка С’ – сама себе тень).

Дата добавления: 2015-07-10 ; просмотров: 1509 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Построение теней в аксонометрии

осью у’ провести вертикальную прямую до пересечения с аксонометрией луча, проходящего через точку А.

Для построения тени отрезка АВ в аксонометрии на рис. 18.10 использована мнимая тень (А₁ Т ) точки А.

На рис. 18.11 построены тени от лестницы и тени от тумбы, имеющей форму усечённого параллелепипеда.

Построения тени от лестницы ясны из чертежа.

На рис.18.11 тени на лестнице от тумбы построены в следующем порядке:

1. Определена тень от вертикального отрезка А’А’₁.

На второй ступеньке тень от отрезка А’В’ строится аналогично. Выполненные построения ясны из чертежа.

Источник

Инженерная графика Методические указания с заданиями на графические работы № 9 «Тени в ортогональных проекциях» и № 10 «Тени в аксонометрии» для студентов дневного отделения специальности 08.02.01 «Строительство и эксплуатация зданий и сооружений» базовой и углубленной подготовки

ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«РЯЗАНСКИЙ СТРОИТЕЛЬНЫЙ КОЛЛЕДЖ»

Методические указания с заданиями на графические работы

№ 9 «Тени в ортогональных проекциях»

и № 10 «Тени в аксонометрии»

для студентов дневного отделения специальности 08.02.01 «Строительство и эксплуатация зданий и сооружений»

базовой и углубленной подготовки

Одобрена Составлена в соответствии

методической комиссией с Федеральным

специальностей 08.02.01 государственным образова-

и 08.02.03 тельным стандартом по

Протокол №_____ специальности 08.02.01

от «____»___________20__г. «Строительство и эксплуа-

тация зданий и сооружений»

В настоящих методических указаниях кратко изложены методические указания по выполнению графических работ «Тени в ортогональных проекциях», «Тени в аксонометрии» и представлены задания на эти работы.

ВВЕДЕНИЕ …………………………………………………. 4 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ

ЗАДАНИЯ НА ГРАФИЧЕСКИЕ РАБОТЫ. …………. 8 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ…. ……..33

В настоящее время в условиях все возрастающей конкуренции на рынке
труда современному выпускнику требуются знания и умения
как в области общепрофессиональных, так и специальных дисциплин.
В строительстве и архитектуре широко используются тени при построении проектируемых зданий, интерьеров, помещений.

Данные методические указания рекомендуются для студентов направления 08.02.01 «Строительство и эксплуатация зданий и сооружений», выполняющих графические работы «Тени в ортогональных проекциях» и «Тени в аксонометрии» по разделу «Строительное черчение».

Целью выполнения данных графических работ является приобретение
знаний, умений и навыков построения теней на фасаде здания, в аксонометрии и некоторых архитектурных форм, что позволит студентам в дальнейшем использовать полученные знания при изучении профилирующих дисциплин и окажет помощь в практической деятельности, как специалиста.

После изучения раздела «Строительное черчение» студент должен:

● о собственных и падающих тенях на фасаде здания;

● способы построения проекций теней на фасадах и архитектурных элементах;

● использование проекций теней в архитектурном проектировании;

● строить проекции теней на фасаде и архитектурных фрагментах зданий;

● строить проекции теней в аксонометрических проекциях зданий.

2 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ

ОБЩИЕ УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ГРАФИЧЕСКОЙ
РАБОТЫ «ТЕНИ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ»

Содержание работы. Построить тени на фасаде здания. Выполнить
отмывку. Индивидуальные задания помещены в приложении Б.

Графическая работа должна быть оформлена в соответствии с ГОСТ
ЕСКД и СПДС и отличаться выразительностью, четкостью, опрятностью.
Задание выполняется карандашом с сохранением всех вспомогательных
построений. Типы и толщины линий должны быть приняты в соответствии с
ГОСТ 2.303-68* «Линии».

Образец выполнения задания показан в приложении А.

ОБЩИЕ УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ГРАФИЧЕСКОЙ
РАБОТЫ «ТЕНИ В АКСОНОМЕТРИИ»

Содержание работы. Построить аксонометрию импровизированного здания, используя задания графической работы № 9, увеличив их в 1,5 раза. Выполнить отмывку.

Образцы выполнения задания показаны в приложении В.