Как построить спектр прямоугольного импульса
Спектр периодической последовательности прямоугольных импульсов
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
В данном разделе мы рассмотрим спектр периодической последовательности прямоугольных импульсов, как одного из важнейших сигналов, используемого в практических приложениях.
Рассмотрим некоторые свойства огибающей спектра периодической последовательности прямоугольных импульсов.
Таким образом, значение огибающей на нулевой частоте равно амплитуде импульса деленной на скважность. При увеличении скважности (т.е. при уменьшении длительности импульса при фиксированном периоде повторения) значение огибающей на нулевой частоте уменьшается.
Используя скважность импульсов выражение (1) можно переписать в виде:
Нули огибающей спектра последовательности прямоугольных импульсов можно получить из уравнения:
Из рисунка 5 следует, что сдвиг периодического сигнала во времени не изменяет амплитудный спектр сигнала, но добавляет линейную составляющую к фазовому спектру сигнала.
В данном разделе мы получили аналитическое выражение для спектра периодической последовательности прямоугольных импульсов.
Мы рассмотрели свойства огибающей спектра периодической последовательности прямоугольных импульсов и привели примеры спектров при различном значении скважности.
Также был рассмотрен спектр при смещении во времени последовательности прямоугольных импульсов и показано, что смещение во времени изменяет фазовый спектр и не влияет на амплитудный спектр сигнала.
Данные для построения рисунков данного раздела были просчитаны при использовании библиотеки DSPL-2.0
Спектр прямоугольного импульса
У меня есть задачка, первая часть которой кажется тривиальной. Нужно написать прогу в матлабе, которая строит спектр любого сигнала. В интернете есть куча разных кодов, но мне хочется написать самой и разобраться.
Для начала я рассматриваю прямоугольный импульс. Строю его амплитудный, фазовый спектры, вещ. и мнимую части, в общем, все инкарнации этого демона.
И вот беда! Какой-то косяк с числовыми значениями по осям. Насколько я понимаю, в теории, например, амплитудный спектр должен иметь максимум, равный площади импульса (длительность*амплитуда). У меня не так. И минимумы этого спектра должны соответствовать значениям (2*пи)/длительность, (4*пи)/длительность и т.д. У меня не так.
Отчаявшись править код, обращаюсь к тебе, великое сообщество программистов! Заранее благодарна.
Вот такой у меня код:
СПМ прямоугольного импульса
Подскажите пожалуйста, как построить аналитическую спектральную плотность мощности прямоугольного.

Здравствуйте, есть следующий код для создания и построения прямоугольного импульса в Matlab: T =.
Поиск спектра прямоугольного импульса
Всем привет, помогите разобраться с проблемой. Задача проста, имеется сигнал- прямоугольный.
Нормировка амплитудного спектра прямоугольного импульса
tay=10^(-4); % длительность импульсов q = 2; % скважность n=1024; Tp=tay*q;% период следования.
Прямоугольные импульсы: описание и принцип формирования
Оценка диапазона пропускания системы
Искажение импульса проявляется в виде отклонений профиля сигнала от «идеального» профиля. Конечно, искажения напрямую влияют не только на форму, но и на добротность. Например, очень часто системе не хватает скорости отклика, чтобы передать вид точной амплитуды сигнала, которая, в свою очередь, меняется слишком быстро.
В основном искажение выходного сигнала происходит вследствие несовпадения ширины полосы пропускания системы со спектральной шириной выходного сигнала. Этот эффект часто наблюдается, когда входной сигнал представляет собой прямоугольную последовательность импульсов с высокой частотой: тогда искаженный прямоугольный импульс будет иметь округлый вид, как это показано на рисунке 1.

Рисунок 1. Пример явного искажения импульса из-за медленного отклика системы
Промежуточная обработка сигнала также приводит к искажениям. Примером является система, состоящая из драйвера лазерного диода, который принимает входной сигнал от функционального генератора и подает токовый сигнал на лазерный диод. Предполагается, что токовый сигнал является наиболее точным представлением входного сигнала, подаваемого генератором функций.
Тем не менее, собрать систему, скорость отклика которой достаточно высока, по-прежнему непросто и реальные условия диктуют несколько другие правила: когда ширина спектральной полосы входного сигнала превышает предельную частоту всей системы (в данной статье рассматривается система с частотным пределом 750 кГц или 3 дБ) искажения в выходном сигнале становятся наиболее заметны.
В своем лабораторном эксперименте компания Thorlabs исследовала разные прямоугольные последовательности импульсов в системе с предельной частотой 750 кГц. Искажение выходных сигналов анализировалось двумя методами: рассмотрение частотного состава входных и выходных сигналов и сравнение формы входных и выходных импульсов. Это сравнение было необходимо для:
О прямоугольной последовательности импульсов
Последовательность прямоугольных импульсов состоит из повторяющихся через равные промежутки времени прямоугольных импульсов, по форме чем-то напоминающих шляпу (цилиндр). Прямоугольная форма возникает из-за того, что сигнал резко возрастает от минимального до максимального значения и задерживается в этом положении некоторое время, затем снова возвращаясь к минимальному (см. рис. 2).
Если бы форма волны на рисунке 2 была построена как функция частоты, ось частоты продолжалась бы до бесконечности. Для создания идеальной последовательности прямоугольных импульсов требуется дискретная возрастающая последовательность частот, таким образом генерируются бесконечно короткие переходы между амплитудами.
Итак, чтобы получать периодический сигнал прямоугольной формы, необходимо множество частот, превышающих основную частоту сигнала (которая обратна величине периода).
Следствия ограничения пропускательной способности системы
Если высокочастотные составляющие «отрезаны» из прямоугольной последовательности импульсов, острые углы прямоугольников скругляются, и минимальное время, необходимое для перехода между состояниями низкой и высокой амплитуды, увеличивается. Если отсекается достаточно много высокочастотных компонентов, входная прямоугольная последовательность импульсов преобразуется в синусоидальную волну.
Полоса пропускания: 3 дБ или 750 Гц?
Диапазон частот системы обычно описывается децибелами (дБ) вместо принятых частотных единиц – герц (Гц). В герцах вычисляется абсолютный диапазон, децибелы более удобны на практике. В рассматриваемом исследовании частотный диапазон системы составляет 3 дБ. Точно определить максимальную частоту, выше которой не воспринимает система, может быть достаточно сложно.
Удобно работать с выходным сигналом, состоящим только из частот ниже предельной, в данном случае ниже 3 дБ. В противном случае система будет сильно ослаблять частоты, превышающие порог, однако эти частоты могут по-прежнему вносить вклад в выходной сигнал.
Частота среза 3 дБ в данном исследовании рекомендуется для использования в качестве общего эталона для оценки того, насколько различен частотный состав выходных и входных сигналов.
Экспериментальная установка
Экспериментальная установка показана на рис. 3. Прямоугольные импульсы поступают от функционального генератора в установку, содержащую лазерный диод LP980‐SA80 Thorlabs и контроллер тока и температуры CLD1010LP Thorlabs. Выходной ток, регистрируемый контроллером, содержит установленную пользователем постоянную компоненту. Ток запускает волоконный лазерный диод, установленный в контроллере. Величина постоянной составляющей тока была выбрана таким образом, чтобы общий ток, посылаемый на лазерный диод, всегда превышал пороговый ток генерации. Модулированный таким образом выходной ток на лазерном диоде позволял получать модулированный оптический сигнал.
Как частота влияет на искажение формы импульса?
Коэффициент заполнения квадратно-импульсной последовательности в основном составляет 50%, ширина импульса (длительность) в этом случае составляет половину периода. Однако абсолютный период колебаний по-прежнему обратно зависит от частоты.
Квадратные импульсные сигналы с различной частотой также подавались в экспериментальную установку. Измеренные выходные импульсы (некоторые из них изображены на рис. 4) демонстрировали более высокое искажение на частотах, близких частоте среза.

Рисунок 3. Выходные сигналы, зарегистрированные после прохождения через систему с частотой, близкой к частоте среза 3 дБ (соответствует 750 кГц ): пороговая частота почти в 9 раз превышает частоту входного сигнала 83,3 кГц (темно-красный), в результате чего выходной сигнал имеет меньше всего искажений
В ходе эксперимента было выявлено, что при повышении частоты длительность импульса понижается, однако время, за которое выходной сигнал переходит между минимумом и максимумом амплитуд, остается без изменений. Это объясняется тем, что по мере увеличения частоты «боковые стороны» импульсов отклонялись от вертикальной оси. Вершина пульса также стала менее плоской с увеличением частоты. Для крайнего случая, когда частота была равна 3 дБ, выходной сигнал напоминал синусоидальную волну.
При исследовании соотношений между частотой сигнала и частотой среза, было использовано разложение квадратно-импульсной последовательности в ряд Фурье:

Принимая во внимание анализ полученного ряда Фурье, в ходе эксперимента отмечались также некоторые наблюдения:
По мере увеличения частоты у некоторых компонентов входного сигнала отмечались частоты ниже предельной. Искажение импульса выходного сигнала было вызвано тем, что компоненты сигнала с частотами выше этого порога были сильно ослаблены системой. В конце эксперимента форма выходного сигнала стала напоминать синусоидальную волну, поскольку все меньше и меньше частотных компонентов имели частоты ниже предельной, их вклад стал незначительным по сравнению с первым слагаемым. Так, когда частота повторений достигла предела, только первая частотная компонента осталась ненулевой.
«Правило девяти» для квадратно-импульсных сигналов
Искажение выходного импульса можно свести к минимуму, если полоса пропускания системы соответствует или превышает ширину спектра входного сигнала. В реальных условиях, когда добиться такого полного соответствия (почти) невозможно, нужно определить минимальный диапазон пропускания системы, при попадании в который выходной сигнал был бы менее всего искажен.
Эмпирическое «правило девяти» может быть хорошим ориентиром для решения многих практических задач. Правило гласит, что полный диапазон пропускания системы должен быть как минимум в девять раз выше частоты входного прямоугольно-импульсного сигнала.
Хотя только «идеальные» прямоугольно-импульсные сигналы имеют коэффициент заполнения 50%, «правило девяти» применимо в случаях, когда коэффициент заполнения близок к 50% (чуть больше или чуть меньше). Однако искажение выходных сигналов с таким коэффициентом заполнения неизбежно. Чтобы приблизить профиль выходного сигнала к идеальному, потребуется увеличить диапазон пропускания как минимум в три раза (воспользоваться правилом).
Основа этого наблюдения лежит в ряде Фурье. Когда частотный предел системы в 9 раз превышает частоту входного сигнала, ряд будет содержать 5 ненулевых частотных компонентов, частота которых ниже предельной. Профиль сигнала для этого случая приведен на рис. 4. Сигнал с частотой 83.3 кГц имеет профиль, который может быть распознан системой как квадратный.
В случае, если ширина диапазона пропускания системы в 3 раза превышает ширину входного сигнала, ряд Фурье содержит уже два ненулевых частотных компонента. То есть для системы диапазоном 750 кГц частота сигнала, подходящего для создания квадратно-импульсной последовательности, составит 250 кГц.
Если подается сигнал, частота которого равна предельной, только первое слагаемое суммы ряда Фурье останется ненулевым. В данном эксперименте подавался сигнал с частотой 750 кГц (соответствующей пороговому значению), на выходе получали синусоидальный профиль.
Влияние на профиль выходного импульсного сигнала снижения коэффициента заполнения (до 20%) обсуждается в следующем разделе.
Как коэффициент заполнения сигнала влияет на профиль и диапазон пропускания системы?
Если частота начального прямоугольно-импульсного сигнала остается постоянной, уменьшение коэффициента заполнения приводит к сокращению ширины импульса*. Уменьшение ширины импульса при неизменной частоте сопровождается более явными искажениями выходного импульса, особенно если ширина полосы пропускания системы меньше ширины спектра сигнала.
Во-первых, качество профиля выходного сигнала ухудшается из-за того, что время перехода между состояниями низкой и высокой амплитуд состояний растет.
Во-вторых, сигналу требуется меньше времени для стабилизации высокой амплитуды, прежде чем перейти к амплитуде в низком состоянии, это также провоцирует «расплывание».
На рисунке 5 показан набор профилей импульсов, измеренных на выходе экспериментальной установки, когда входной сигнал имел коэффициент заполнения 20%.

Рисунок 5. Кривые амплитуд выходных сигналов с указанной частотой каждого из них: в этой части эксперимента коэффициент заполнения снижен до 20%, снижение коэффициента заполнения особенно повлияло на профиль импульса сигнала частотой 83.3 кГц (см. рис. 3)
Профиль импульса был узнаваемо прямоугольным для частоты повторений 83.3 кГц, когда ширина полосы пропускания системы была примерно в девять раз больше ширины спектра входного сигнала. Когда частота входного сигнала составляла 200 кГц, диапазон пропускания системы превышал частоту входного сигнала в три раза, однако выходной импульс имел уже синусоидальную форму из-за снижения коэффициента заполнения импульса. В предыдущем опыте он составлял 50%, тогда еще более высокая частота входного сигнала (250 кГц) позволяла получать прямоугольный профиль выходного сигнала.
* Время, в течение которого сигнал находится в состоянии высокой амплитуды.
Сравнение коэффициентов заполнения входного и выходного сигналов
Увеличение частоты входного импульсного сигнала, коэффициент заполнения импульса которого не равен 50%, вызывает искажения в профиле выходного сигнала. В результате можно получить такой сигнал, коэффициент заполнения импульса которого и составляет 50%.
Демонстрация этой тенденции для установки с пределом пропускания 750 кГц, описанной в работе ранее, представлена на рисунке 6.

Рисунок 6. Кривые коэффициентов заполнения входного и выходного импульсного сигналов по мере увеличения частоты вплоть до порогового значения 750 кГц: высокочастотные компоненты урезаны, коэффициент заполнения выходного сигнала составил 50 %
Этот эффект обусловлен тем, что основная частотная составляющая входного сигнала (собственная частота) является графиком синусоиды. Синусоидальные волны имеют коэффициент заполнения 50%, а высокочастотные составляющие необходимы для преобразования формы волны в сигнал с желаемым коэффициентом заполнения. Увеличение частоты начального импульсного сигнала приводит к увеличению числа ненулевых компонентов в ряде Фурье, частоты которых превышают предел системы (3 дБ). Поскольку эти высокочастотные компоненты практически полностью режутся в системе, в выходном сигнале преобладает основная частотная составляющая.
Количественное измерение искажений
Оценка добротности сигнала необходима для прогнозирования и расчета номинального искажения импульса и допустимых параметров. Популярным методом оценки искажений сигнала является преобразование Фурье: на практике часто анализируют и обрабатывают последовательности, полученные через разложение в ряд исходного сигнала. С помощью преобразования Фурье получают «идеальные» импульсные последовательности сигналов с прямоугольным профилем, а затем сравнивают фактические данные. Сравниваются главным образом длительности реального и «идеального» импульсов.
На рис. 7 показан период идеального прямоугольного импульса (зеленый) и период синусоиды (синий). Синусоида – первое слагаемое в сумме ряда Фурье этого импульсного сигнала. Пунктирные линии демонстрируют «расплывание».

Рисунок 7. Прямоугольно-импульсный сигнал (зеленый) и синусоидальный (синий) имеют ширину спектральной полосы, равную 0.5Т: пунктирные линии показывают переходы от низкого к высокому состоянию амплитуды, для прямоугольной волны переход является бесконечно коротким и время пребывания в каждом состоянии равно 0.5T, для синусоидального сигнала верно обратное
Добротность сигнала – это шкала от 0 до 1, единица описывает импульсы с идеальными прямоугольными профилями с бесконечно малым временем перехода между минимальной и максимальной амплитудами. Ноль соответствует сигналам, время перехода от максимальной до минимальной амплитуды которых будет равно длительности идеального прямоугольного импульса. Например, синусоидальный импульс на рисунке 7 имеет нулевой коэффициент добротности, поскольку его время перехода от минимума до максимума составляет половину периода и равно ширине идеального прямоугольного импульса.
Шумы и частотная нестабильность затрудняют снятие точных измерений времени перехода между амплитудами у реальных сигналов. Вместо этого обычно производится измерение времени, необходимого для перехода от точки, немного превышающей минимальную амплитуду, в другую точку, немного ниже максимальной амплитуды. Обычно это точки расположены на уровне 10% и 90% по шкале амплитуды вверх по переднему фронту. Коэффициент добротности Г рассчитывается через время нарастания импульса τr, а также ширину идеального прямоугольного импульса W:

Измерение добротности сигнала
Синяя кривая на рисунке 8 показывает коэффициенты добротности, рассчитанные для выходных импульсов, когда входные сигналы имели 50% коэффициент заполнения и частоты между 25 кГц и 750 кГц.

Рисунок 8. Периодические прямоугольные последовательности импульсов поступали в экспериментальную установку с предельной частотой 750 кГц, для каждого сигнала рассчитывались коэффициенты качества выходных сигналов*, две кривые, полученные в опытах, где коэффициент заполнения импульсов составлял 80%, показали наиболее высокое качество выходного сигнала (линии, соединяющие точки данных, построены для наглядности)
* Кривые коэффициентов заполнения приводятся с отметкой «High» или «Low». Это указывает на то, как именно проводился сравнительный анализ: в верхнем или нижнем амплитудном состоянии соответственно.
Показатель добротности, рассчитанный для случая частоты входного сигнала 83.3 кГц, составил 0.87, что достаточно высоко. Серия опытов с сигналами такой частоты как раз осуществлялась по «правилу девяти», о котором говорится выше.
Коэффициент добротности 0.58, рассчитанный для частоты 250 кГц при коэффициенте заполнения 50% подтверждает следующее качественное наблюдение: несмотря на некоторое искажение импульса в выходном сигнале, профиль импульса был скорее прямоугольным, чем синусоидальным, даже если только две частотные компоненты ряда Фурье входного сигнала лежали в пределах полосы пропускания системы.
Когда частота повторения составила 750 кГц, выходной сигнал оказался синусоидальным, а добротность при этом была нулевой.
Показатели добротности для случая коэффициента заполнения 20% показаны красным цветом.
Коэффициент добротности 0.68 сигнала с частотой 83.3 кГц соответствует прямоугольному профилю выходной последовательности импульсов. Однако прослеживается больше искажений профиля, чем в предыдущем пункте, когда коэффициент заполнения составлял 50%.
Опыт показывает, что уменьшение коэффициента заполнения при сохранении частоты повторения приводит к увеличению искажений профиля выходного сигнала. Чтобы повысить коэффициент добротности до 0.87, частоту сигнала с коэффициентом заполнения 20% необходимо снизить приблизительно до 33 кГц.
Когда частота сигнала с коэффициентом заполнения 20% была увеличена до 250 кГц, добротность стала равна нулю. Дальнейшее увеличение частоты сигнала с коэффициентом заполнения 20% привело к отрицательным показателям добротности. Физически это означает, что время нарастания было больше, чем ширина входного импульса. При таком сигнале добиться приемлемой точности при дальнейшей обработке крайне сложно.
Зеленая кривая (80% High) демонстрирует следующее: если коэффициент заполнения входного сигнала превышает 50%, минимальная добротность является уже положительной. Поскольку шкала в этой серии начинается не от нуля, показатели добротности трудно сравнить с другими значениями коэффициента заполнения.
Кроме того, добротность, рассчитанная по высокоамплитудной части импульса, низкоамплитудную составляющую не учитывает, как не учитываются и все содержащиеся в ней искажения. В таком случае можно рассчитать добротность при минимальной амплитуде. Эти альтернативные данные отмечены желтым и, как ожидалось, напоминали кривые, полученные для сигналов с коэффициентом заполнения 20%.
Показатели добротности, показанные на рисунке 8, отображают влияние ширины импульса, частоты и коэффициента заполнения входного сигнала на профиль выходного сигнала. Когда другие параметры неизменны, искажение выходного сигнала может возрасти по следующим причинам:
Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Thorlabs на территории РФ
Спектр одиночного прямоугольного импульса
Одиночный импульс можно рассматривать как непериодический сигнал, так как не существует конечного интервала времени T, отвечающего условию
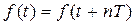
Наиболее просто и наглядно спектр непериодического сигнала можно получить из спектра периодического сигнала (1.16), принимая, что период T стремится к бесконечности, т.е. путем предельного перехода от ряда Фурье к интегралу Фурье
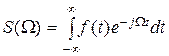
Величину S(W) называют спектральной функцией или просто спектральной плотностью.
Рассчитаем спектральную плотность одиночного прямоугольного импульса длительностью t (рис. 1.9).
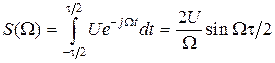
Последнее выражение может быть представлено в несколько ином виде:
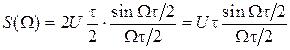
Здесь текущая частота W может принимать любые значения от нулевой до бесконечно большой (сплошной спектр). График для S(W) приведен на рис. 1.10.
 |
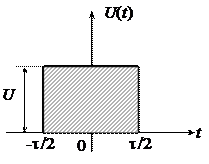 |
| Рис. 1.9. Прямоугольный импульс | Рис. 1.10. Спектр амплитуд прямоугольного импульса |
При частотах W = 2kp/t (k = 1, 2, 3,…) спектральная плотность S(W) = 0. Учитывая характер распределения S(W), можно отметить, что требуемая полоса частот вполне определяется спектром в пределах первого (k =1) нулевого значения спектральной плотности. При этом W = 2p /t = 2p .. F, где F = 1/t. Таким образом, для непериодического сигнала необходимая полоса частот может быть найдена из уравнения
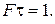
Данный вывод вытекает и из того, что энергия непериодического сигнала пропорциональна интегралу от квадрата спектральной плотности
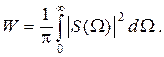
Если спектр сигнала ограничивается частотой Wmax, то энергия уменьшается до значения
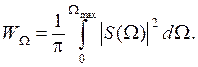
Зависимость энергии WW от наибольшей частоты ограничения Wmax спектра прямоугольного импульса показана на рис. 1.11.
Из рис. 1.10 и 1.11 следует, что наибольшее энергетическое значение имеют составляющие низкочастотной части спектра импульса. С ростом ширины сохраняемой части спектра от нуля до величины Wmax= 2p/t энергия WW быстро увеличивается и достигает 90 % всей энергии W. При дальнейшем увеличении спектра энергия WW нарастает все медленнее. Таким образом, при ширине спектра Wmax= 2p/t или F=1/t обеспечивается передача значительной части энергии сигнала. Чем короче импульс, тем более широкий спектр должен быть сохранен.
Рис. 1.11. Зависимость энергии импульса от ширины сохраняемой части спектра
Итак, мы рассмотрели как сообщения (первичные сигналы), с которыми приходится иметь дело в телемеханике, так и переносчики, с помощью которых они передаются. Прежде чем переходить к изучению методов образования сигналов, остановимся на некоторых вопросах преобразования непрерывных сообщений в дискретные. Такое преобразование имеет место в цифровых телеизмерительных системах, в системах связи при передаче речи, музыки, телевизионных изображениях и т.п.
Дата добавления: 2016-02-04 ; просмотров: 5531 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ






