Как построить синусоиду по точкам

Основные понятия

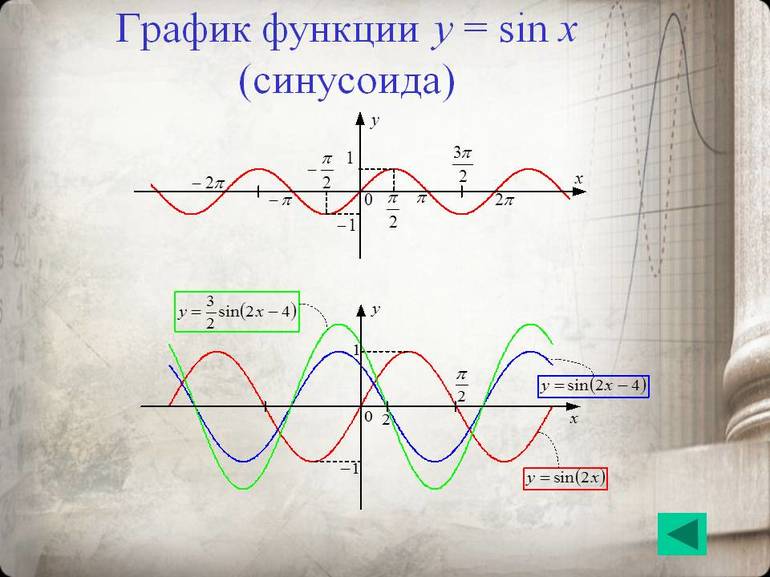
Кривая получается из синусоидальной дуги путём смещения к пи/2 в сторону со знаком минус. Кривая представляет график функции у=sin x. В формуле синусоиды y=a+b cos (cx+d) присутствуют следующие аргументы:

Сжатие, растяжение либо сдвиг кривой приводит к изменению величины. Явления называются гармоническими колебаниями. Примеры синусоиды: экспонент или показательная функция в виде винтовой линии, проведённой на плоскости, скрученный провод, развёрнутый рулон бумаги.

Особенности построения

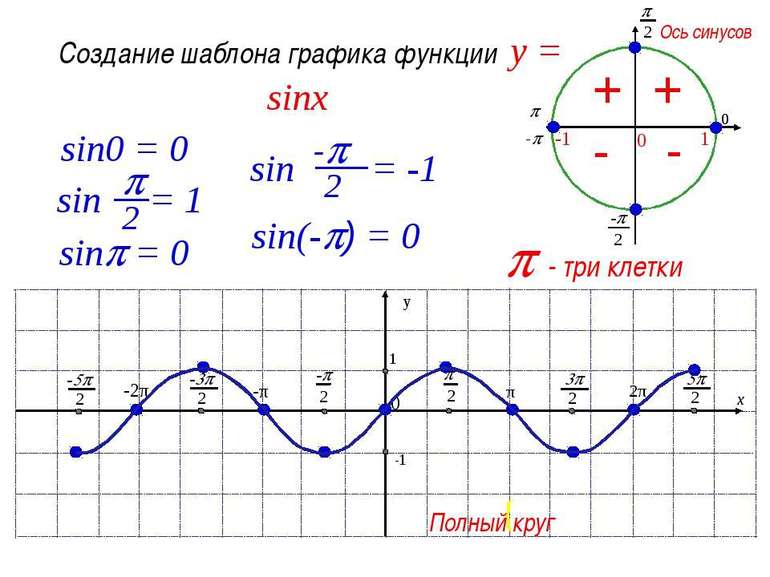
Чтобы выявить свойства синусоиды, необходимо построить её график, провести исследование синуса. В алгебре под функцией представлена плоская кривая, которая выражает закон колебания sin с учётом изменения центрального угла. Сама синусоида строится в схематической последовательности:

График можно построить на онлайн ресурсе либо с помощью специальных программ (Excel). Для расчёта используется калькулятор, основная формула y=sin х. При решении задач учитывается длина волны, которая равна 2 пи. Такое преобразование объясняется тем, что значение функции при любом икс совпадает с её периодичностью x+2π.

При сдвиге графика влево к значению пи/2 образуется косинусоида. Любое изменение величины характерно для квадрата с гармоническими колебаниями. Примеры подобных явлений: движение маятника, сбои с напряжением в электросети. Другой случай с синусоидальными колебаниями — звук. Он редко бывает чистым, соответствуя y=A sin wt, где:

Чаще издаются обертоны, для которых характерны низкие амплитуды. Подобные явления изучаются в школе на уроках физики в старших классах.

Свойства и доказательства

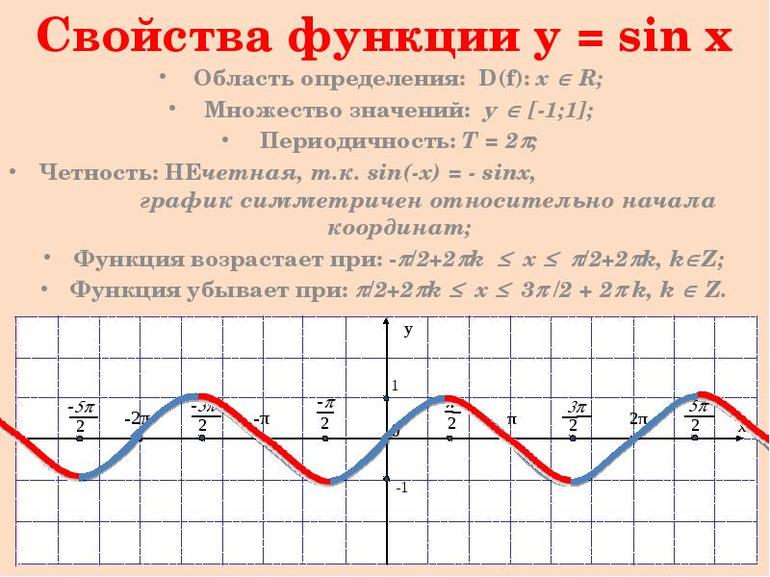
К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.

Так как через круг в одной области можно провести только одну прямую, перпендикулярную оси, поэтому для области определения функции подходят все числа. Такое свойство записывается следующим образом: D (sin x) = R.

Нечётность и постоянство

Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.

Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.

Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.

Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.

Больше и меньше

С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.

Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.

Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.

Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.

Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.

Источник

Функция y = sin x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).

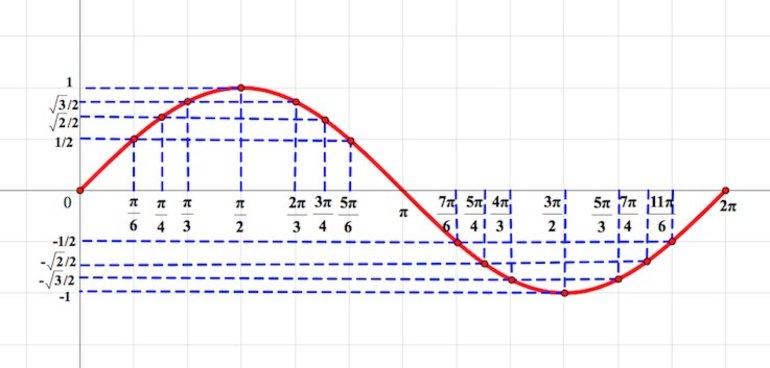
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.

п.2. Свойства функции y=sinx⁡

2. Функция ограничена сверху и снизу

Область значений \(y\in[-1;1]\)

3. Функция нечётная

4. Функция периодическая с периодом 2π

5. Максимальные значения \(y_=1\) достигаются в точках

Минимальные значения \(y_=-1\) достигаются в точках

Нули функции \(y_<0>=sinx_0=0\) достигаются в точках \(x_0=\pi k\)

6. Функция возрастает на отрезках

Функция убывает на отрезках

7. Функция непрерывна.

п.3. Примеры

Пример 2. Решите уравнение графически:
a) \(sinx=3x\)

Один корень: x = 0

б) \(sinx=2x-2\pi\)

Один корень: x = π

в) \(sinx-\sqrt=0\)
\(sinx=\sqrt\)

Один корень: x = π

Источник

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть

Источник

Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.

Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида. Вариант для печати.

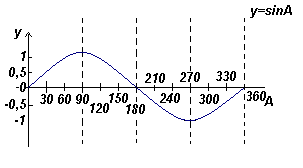График функции y=sinA (синусоида)	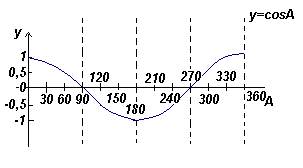График функции y=cosA (косинусоида)
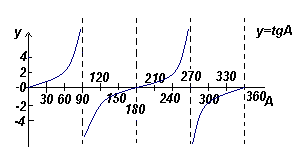График функции y=tgA (тангенсоида)

Из графиков видно что:

Углы произвольной величины

График. Положительное или отрицательное направление при движении по окружности.

График. Поcтроение углов в различных квадрантах.

Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины.
График. Нахождение всех углов по заданному значению синуса (пример)

Пример 1

График. Нахождение всех углов по заданному значению синуса (пример)

Примечание. Калькулятор дает только один ответ.
График. Нахождение всех углов по заданному значению синуса (пример)

Пример 2

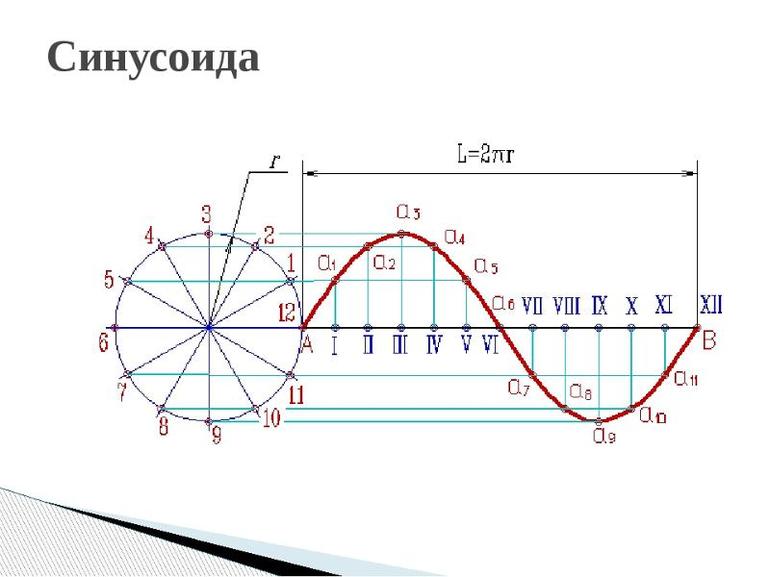
Построение синусоиды и косинусоиды

График. Построение синусоиды.

Из определения тригонометрических функций
sin30 o =TS/TO=TS/1, т.е. TS= sin30 o и cos30 o =OS/TO=OS/1, т.e. OS=cos30 o

Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30 o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.

Синусоидальные и косинусоидальные графики

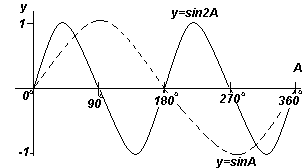График. y=sinA и y=sin2A (синусоиды).	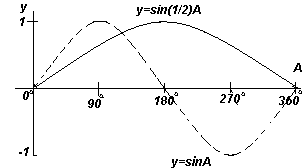График. y=sinA и y=sin(1/2)A (синусоиды).
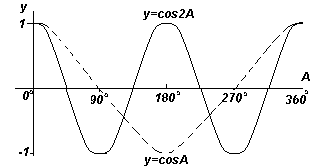График. y=cosA и y=cos2A (косинусоиды).	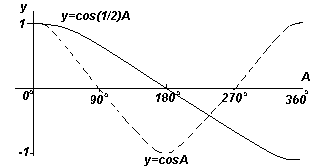График. y=cosA и y=cos(1/2)A (косинусоиды).

Пример 4.
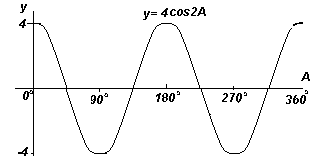
Построить график y=4cos2x в диапазоне от х=0 o до х=360 o

График. Построение y=4cos2x (косинусоида).

Пример 5.
Построить график y=5sin(A+30 o ) в диапазоне от А=0 o до А=360 o

Решение:
Амплитуда = 7, период =2π/2= π радиан
В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p, следовательно 7sin(2A-π/3) запаздывает относительно 7sin2A на ( π/3)/2, т.е. на π/6 радиан или на 30 o
График. y=7sin2A и y=7sin(2A-п/3) (синусоиды).

Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.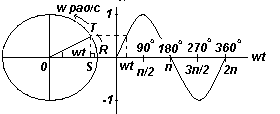

Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором. Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.
График. Фазовый угол. Сдвиг по фазе.

Пример 7.
Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)

Пример 8.
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α).

Решение
Амплитуда = максимальное смещение = 3м
Угловая скорость ω=2πf = 2π(55) = 110 πрад./с
Следовательно, смещение 3sin(110πt + α) м.
При t=0 смещение = 100см=1м.
Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следовательно α=arcsin0,33=19 o
Итак, смещение равно 3sin(110 πt + 0,33).

График. Колебательный механизм (пример, синусоида).

v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35 o или 0,611 рад.
40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс

Источник

Тригонометрические функции

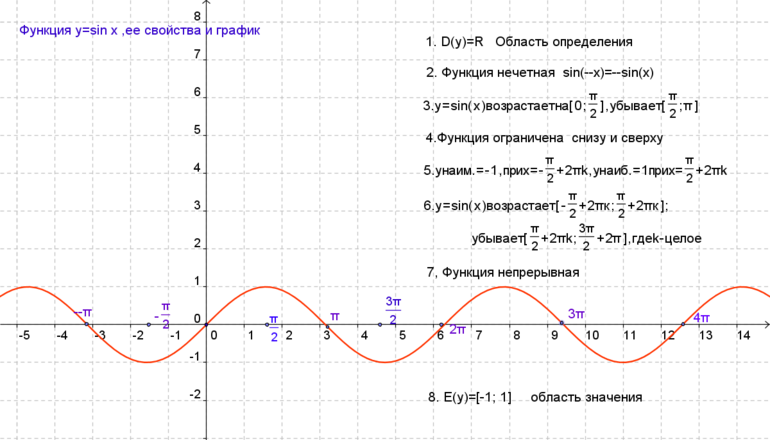
1. Начнем с построения графика функции y = sin x.

Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.

Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть

Это значит, что функция y = sin x является периодической. Мы уже построили уча-сток графика длиной 2π. А теперь мы как будто «копируем» этот участок и повторяем его с периодом 2π:

Синусоида построена.
Перечислим основные свойства функции y = sin x.

Перечислим основные свойства функции y = cos x.

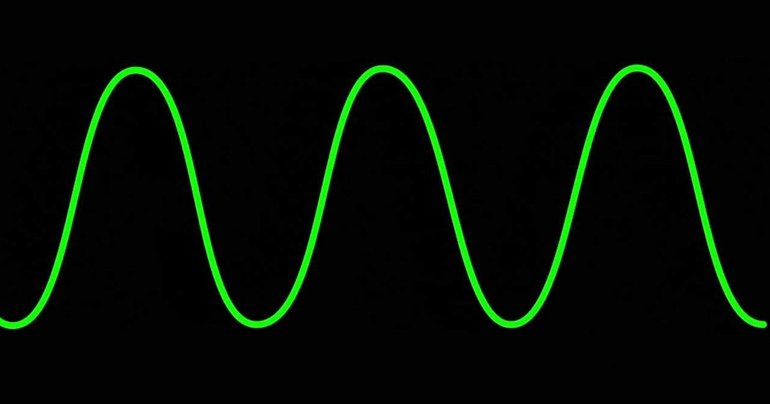
Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!

3. Перейдем к графику функции y = tg x.

Осталось только «скопировать» этот участок графика и повторить его с периодом π.

Перечислим свойства функции y = tg x.

5) Функция y = tg x возрастает при то есть на каждом участке, на котором она непрерывна.

4. График функции y = ctg x строится аналогично. Вот он:

5) Функция y = сtg x убывает при то есть на каждом участке, на котором она непрерывна.

Источник