Как построить шестиугольник вокруг окружности

Правильный шестиугольник и его свойства

Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

Описанная окружность и возможность построения

Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

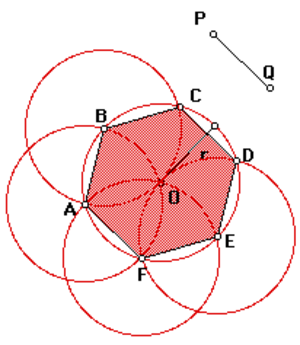
Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

Площадь нового шестиугольника можно посчитать так:

Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

Источник

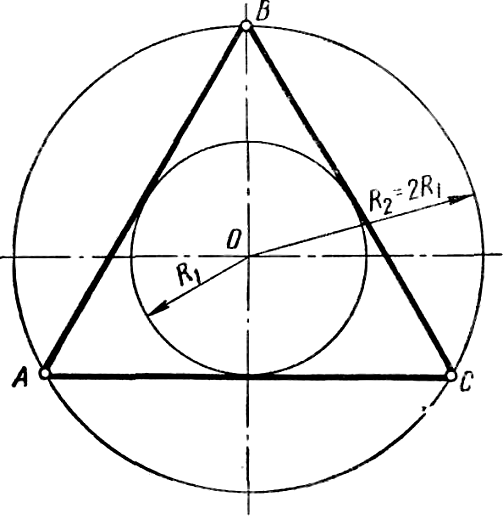
Построение правильных многоугольников, описанных около окружности;

Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R₁ проводят окружность радиусом R₂ = 2R₁ и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R₁.

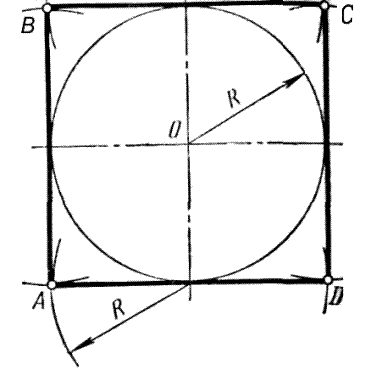
Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D. Точки A, B, C, D и являются вершинами квадрата, описанного около данной окружности.

Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.

Остальные вершины C и F определяют с помощью дуги окружности радиуса OA, которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ

Источник

Шестиугольник описанный около окружности построение

Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

Описанная окружность и возможность построения

Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

Площадь нового шестиугольника можно посчитать так:

Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

Презентация была опубликована 5 лет назад пользователемГригорий Оськин

Похожие презентации

Презентация на тему: » а) Для построения правильного шестиугольника можно воспользоваться тем, что а 6 = R. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую.» — Транскрипт:

2 а) Для построения правильного шестиугольника можно воспользоваться тем, что а 6 = R. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. (таким образом окружность разделиться на 6 равных частей). 4. Соединив последовательно данные точки, получим правильный шестиугольник. б) Для построения правильного шестиугольника можно воспользоваться другим способом (см. учебник стр.206, п. 117).

3 Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. (таким образом окружность разделиться на 6 равных частей). 4. Соединив последовательно через одну данные точки, получим правильный треугольник. Для построения правильного треугольника воспользуемся тем же алгоритмом, что и для построения правильного шестиугольника, только получив 6 точек на окружности, соединим их через одну.

4 Построение. 1. Строим ω(О; R). О 4. Соединив последовательно точки пересечения прямых с окружностью, получим правильный треугольник. Для построения правильного четырехугольника следует провести две перпендикулярные прямые, проходящие через центр окружности. Соединив последовательно точки пересечения прямых с окружностью, получим правильный четырехугольник (квадрат). 2. Проведем произвольную прямую, проходящую через центр окружности. 3. Проведем прямую, перпендикулярную данной и проходящую через центр окружности.

5 Построение. О 3. Соединив последовательно точки на окружности получим правильный восьмиугольник. Для построения правильного восьмиугольника сначала строим правильный четырехугольник ( по описанному алгоритму), а затем проводим две прямые через середины противолежащих сторон. При этом окружность окажется разделенной на 8 раваных частей. Соединив последовательно точки на окружности, получим правильный восьмиугольник. 1. Строим правильный четырехугольник, вписанный в окружность. 2. Проводим две прямые через середины сторон квадрата (вершины квадрата и точки пересечения прямых с окружностью делят окружность на 8 равных частей).

6 Рассмотренные способы построения правильных многоугольников дают возможность построить многоугольники, вписанные в окружность. Чтобы построить многоугольник, описанный около окружности, пользуются теми же способами, только на последнем этапе не соединяют полученные точки на окружности, а проводят через них касательные. Построим правильный шестиугольник, описанный около окружности. Построение. 1. Строим ω(О; R). О 2. Строим произвольную точку, принадлежащую окружности. 3. Из данной точки раствором циркуля равным R на окружности откладываем последовательно один за другим отрезки. 4. Через каждую полученную точку на окружности проводим касательные. Получим правильный шестиугольник.

Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R₁ проводят окружность радиусом R₂ = 2R₁ и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R₁.

Правильный описанный четырехугольник (квадрат) можно построить с помощью циркуля и линейки (рисунок 39). В заданной окружности проводят два взаимно перпендикулярных диаметра. Приняв точки пересечения диаметров с окружностью за центры, радиусом окружности R описывают дуги до взаимного их пересечения в точках А, В, С,D. Точки A, B, C, D и являются вершинами квадрата, описанного около данной окружности.

Для построения правильного описанного шестиугольника необходимо вначале построить вершины описанного квадрата указанным выше способом (рисунок 40, а). Одновременно с определением вершин квадрата заданную окружность радиуса R делят на шесть равных частей в точках 1, 2, 3, 4, 5, 6 и проводят вертикальные стороны квадрата. Проведя через точки деления окружности 2–5 и 3–6 прямые до пересечения их с вертикальными сторонами квадрата (рисунок 40, б), получают вершины А, В, D, Е описанного правильного шестиугольника.

Остальные вершины C и F определяют с помощью дуги окружности радиуса OA, которая проводится до пересечения ее с продолжением вертикального диаметра заданной окружности.
3 СОПРЯЖЕНИЯ

Дата добавления: 2014-11-06 ; Просмотров: 4403 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Как нарисовать шестиугольник в круге

Popular

Основы черчения

Строительное

Машиностроительное

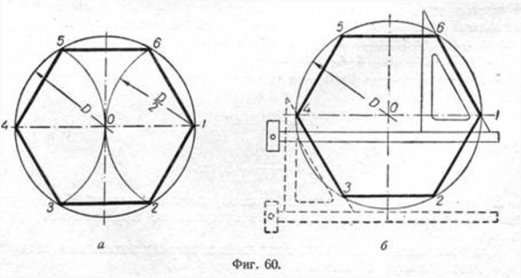
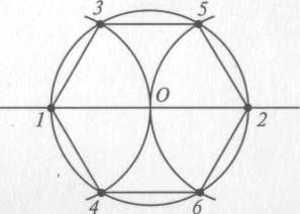
Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

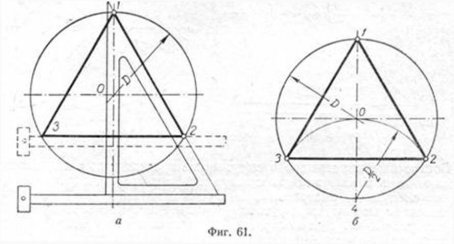
Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

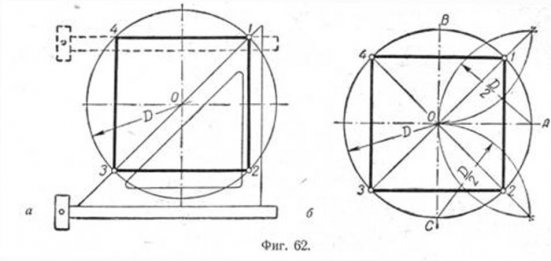
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

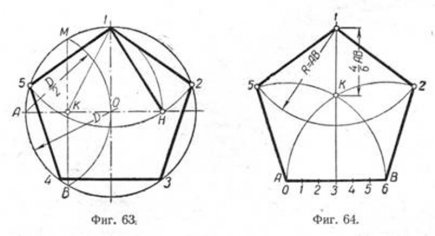
Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

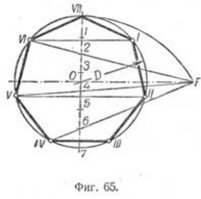
Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

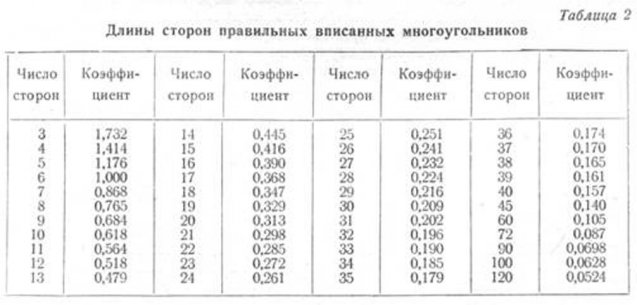
Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.

Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.

Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.

В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.

Способ вычерчивания шестиугольника циркулем, линейкой

Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.

Метод выглядит следующим образом:

Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.

Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.

Способ вычерчивания шестиугольника без циркуля

Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.

Способ построения выглядит следующим образом:

Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.

Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.

Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.

В последнем случае удобнее несколько изменить технологию:

Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.

Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.

Источник