Как построить сечение четырехугольной пирамиды

Как построить сечение четырехугольной пирамиды

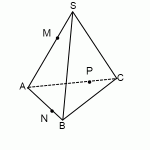
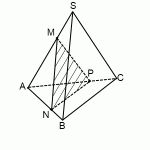
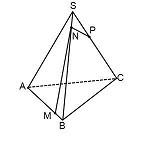
Постройте сечение четырёхугольной пирамиды, проходящее через точки M, N и P. Для случая, когда все рёбра пирамиды равны, определите вид треугольника, являющегося сечением.

Точки M и N лежат в одной плоскости, ребро пирамиды соединяет их и является следом искомого сечения. Аналогично, ребро NP пирамиды является следом искомого сечения. Точки M и P лежат в одной плоскости, следовательно, через них можно провести отрезок, являющийся следом искомого сечения. Поскольку он невидимый, проведем MP пунктирной линией. Треугольник MNP — искомое сечение.

В случае, когда все ребра пирамиды равны, треугольник, являющийся сечением — равнобедренный.

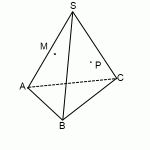
Постройте сечение четырёхугольной пирамиды, проходящее через точки M, N и P. Для случая, когда все рёбра пирамиды равны, определите вид треугольника, являющегося сечением.

Аналоги к заданию № 1782: 1783 Все

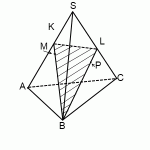
Постройте сечение четырёхугольной пирамиды, проходящее через точки M, N и P. Для случая, когда все рёбра пирамиды равны, определите вид треугольника, являющегося сечением.

Точки M и N лежат в одной плоскости, следовательно, через них можно провести отрезок, являющийся следом искомого сечения. Поскольку он видимый, проведем MN сплошной линией. Аналогично, строим отрезок NP, являющийся следом искомого сечения. Точки M и P лежат в одной плоскости, следовательно, через них можно провести отрезок, являющийся следом искомого сечения. Поскольку он невидимый, проведем MP пунктирной линией. Треугольник MNP — искомое сечение.

В случае, когда все ребра пирамиды равны, треугольник, являющийся сечением — равнобедренный.

Источник

Презентация по геометрии «Построение сечения пирамиды»

Описание презентации по отдельным слайдам:

Построение сечений многогранников

Сечение Секущей плоскостью тетраэдра (параллелепипеда) называют любую плоскость по обе стороны от которой имеются точки донного тетраэдра (параллелепипеда). Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам. Многоугольник, который образован этими отрезками, является сечением фигуры

Построение сечения. Если секущая плоскость пересекает две противоположные грани по каким то отрезкам, то эти отрезки параллельны. Для построения сечения достаточно построить точки пересечения секущей с ребрами тетраэдра (параллелепипеда). Через любые две точки лежащие на одной грани можно провести прямую и при том только одну.

Дана пирамида SABCD.

Требуется построить сечение заданной пирамиды плоскостью, проходящей через точки: М на ребре AS, P на ребре CS и Q на ребре DS. M P Q

M P Q Точки M и Q лежат в плоскости грани АSD. Линия МQ, соединяющая эти точки является линией пересечения плоскости сечения и плоскости грани ASD.

M P Q Линия QP, соединяющая заданные точки Q и P, является линией пересечения плоскости сечения и плоскости грани DSC.

M P Q Линии MQ и AD лежат в одной плоскости грани ASD. Найдём точку Е, как точку пересечения линий MQ и AD. Точка Е будет принадлежать искомой плоскости сечения, так как она принадлежит линии MQ, лежащей в этой плоскости. Е

M P Q Е Линии PQ и CD лежат в одной плоскости грани CSD. Найдём точку F, как точку пересечения линий PQ и CD. Точка F, как и точка Е, будет принадлежать искомой плоскости сечения, так как она принадлежит линии PQ, лежащей в этой плоскости. F

M P Q Е F Точки Е и F принадлежат плоскости сечения и плоскости основания пирамиды, поэтому линия EF будет линией пересечения плоскости сечения и плоскости основания пирамиды.

M P Q Е F Линии EF и BC лежат в одной плоскости основания пирамиды ABCD. Найдём точку G, как точку пересечения линий EF и BC. Точка G будет принадлежать искомой плоскости сечения, так как она принадлежит линии EF, лежащей в этой плоскости. G

M P Q Е F G Точки P и G принадлежат плоскости сечения и плоскости грани BSC, поэтому линия PG будет линией пересечения плоскости сечения и плоскости грани BSC.

M P Q Е F G H PH будет линией пересечения плоскости сечения и плоскости грани BSC.

M P Q Е F G H Ну и наконец, так как точки M и H одновременно принадлежат и плоскости сечения и плоскости грани ASB, то линия MH будет линией пересечения этих плоскостей.

M P Q H И четырёхугольник MHPQ будет искомым сечением пирамиды SABCD плоскостью, проходящей через заданные точки M, P, Q. A D B C

Дана трёхгранная призма A B C A1 B1 C1. Требуется построить сечение призмы плоскостью, проходящей через три заданные точки D, E, и F. A B C A1 B1 C1 D E F

Точки D и E принадлежат плоскости грани А А1 С1 С и плоскости сечения, следовательно линия DE будет линией пересечения этих плоскостей. A B C A1 B1 C1 D E F

Точки E и F принадлежат плоскости грани B C C1 B1 и плоскости сечения, следовательно линия EF будет линией пересечения этих плоскостей. A B C A1 B1 C1 D E F

Линии DE и A A1 лежат в плоскости грани A A1 C1 C. Найдём точку G, пересечения этих линий. A B C A1 B1 C1 D E F G

Точка G принадлежит плоскости сечения, так как она принадлежит линии DE. Точки G и F принадлежат плоскости грани A A1 B1 B и плоскости сечения, следовательно линия GF будет линией пересечения этих плоскостей. A B C A1 B1 C1 D E F G

В плоскости грани A A1 B1 B линии GF и A1 B1 пересекаются в точке L. Точки F и L принадлежат плоскости грани A A1 B1 B и плоскости сечения, следовательно линия FL будет линией пересечения этих плоскостей. A B C A1 B1 C1 D E F G L

Точки D и L принадлежат плоскости основания призмы A1 B1 C1 и плоскости сечения, следовательно линия DL будет линией пересечения этих плоскостей. A B C A1 B1 C1 D E F G L

А четырёхугольник DEFL будет искомым сечением трёхгранной призмы плоскостью, проходящеё через три заданные точки D,E,F. A B C A1 B1 C1 D E F L

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-697342

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Хабаровске родители смогут заходить в школы и детсады только по QR-коду

Время чтения: 1 минута

НИУ ВШЭ откроет первую в России магистратуру по управлению низкоуглеродным развитием

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Минздрав включил вакцинацию подростков от ковида в календарь прививок

Время чтения: 1 минута

Большинство родителей в России удовлетворены качеством образования в детсадах

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Глава 2. Практическое изучение видов сечений и методов их построения в правильной четырехугольной пирамиде

Изучить методы построения сечений в правильной четырехугольной пирамиде можно путем решения задач, включающих в себя элементы построений подобных сечений.

Задача 1 уровня сложности:

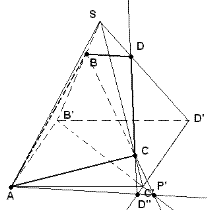
1. Постройте сечение правильной четырехугольной пирамиды плоскостью, через точки, указанные на рисунке.

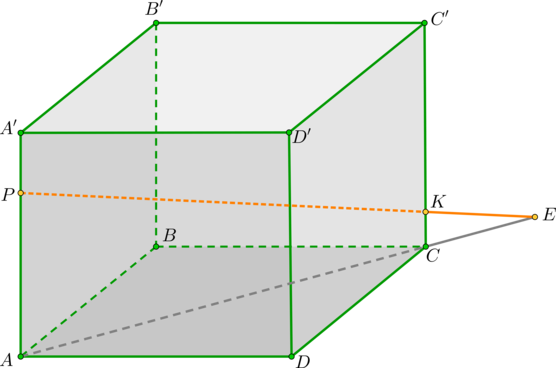
А) проецируем на плоскость основания, путем центрального проецирования из вершины, точки В и С, получая точки: B’ и C’.

Б) пересекаем прямые B’C’ и BC, находим точку P’

В) пересекаем AP’ и D’C’, находим точку D”.

Г) пересекаем D”C и SD’, находим D

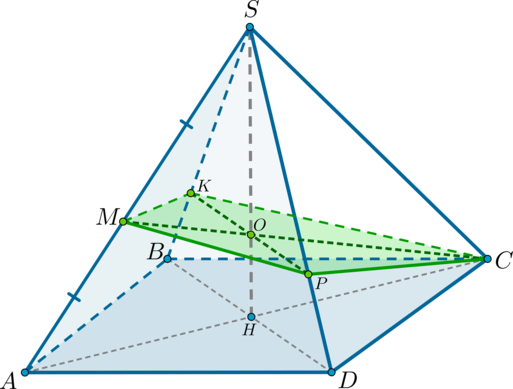
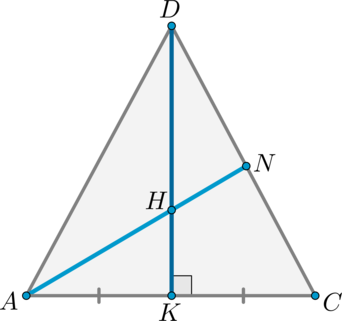
2. Построить сечение четырехугольной пирамиды S_ABCD плоскостью, проходящей через точки M ∈ SB, N ∈ SC, K ∈ AD.\

Краткая запись построения:
1) прямая MN;
2) MN ∩ BC = X;
3) прямая XK;
4) XK ∩ DC = P;
5) XK ∩ AB = Y;
6) прямая YM;
7) YN ∩ SA = Q;
8) прямая PN;
9) прямая KQ;
10) MNPKQ — искомое сечение.

Задача 2 уровня сложности:

SABCD — четырехугольная пирамида. Точка Р лежит в грани SCD, а точка F на продолжении ребра DC так, что точка D лежит между F и С. Постройте сечение пирамиды плоскостью PFB.

Источник

Построение сечений

Определение

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Замечание

Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.

Важные определения

1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.

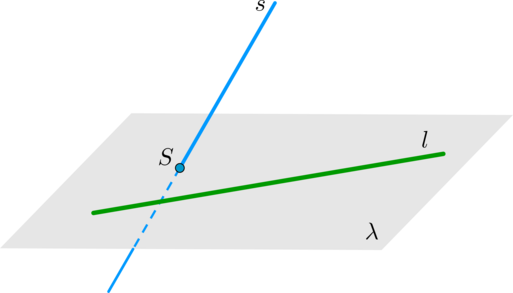
3. Прямая и плоскость параллельны, если они не имеют общих точек.

4. Две плоскости параллельны, если они не имеют общих точек.

6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

Важные аксиомы

1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Важные теоремы

3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

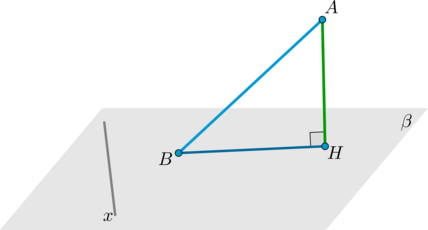
7. Теорема о трех перпендикулярах.

8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.

Замечание

Еще один важный факт, часто использующийся для построения сечений:

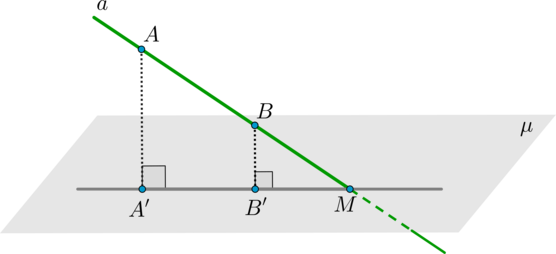
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.

Причем заметим, что все точки \(A, B, A’, B’, M\) лежат в одной плоскости.

Пример 1.

Решение

Пример 2.

Решение

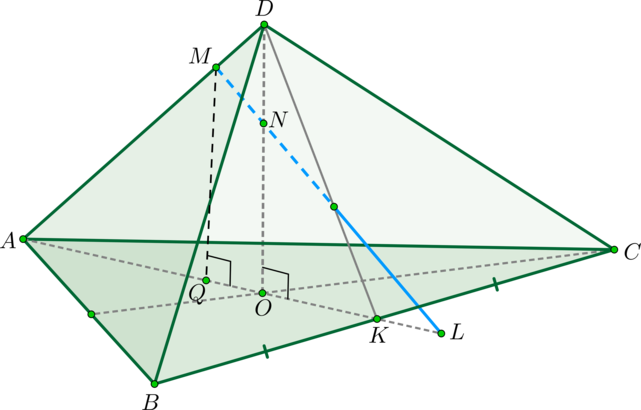
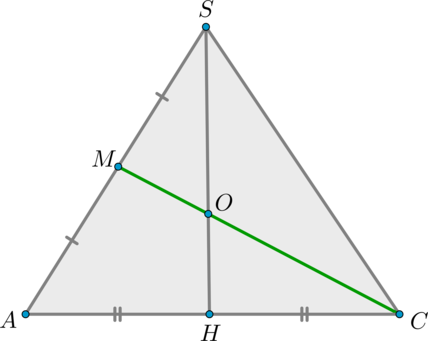
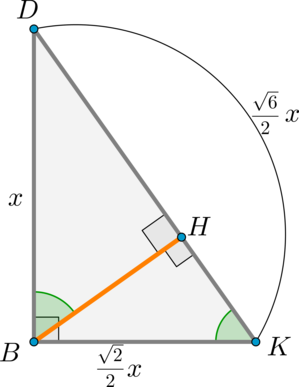
а) \(\triangle AMQ\sim \triangle ADO\) по двум углам ( \(\angle Q=\angle O=90^\circ, \ \angle A\) – общий). Значит,

\[\dfrac=\dfrac=\dfrac=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \ AQ=\dfrac 45\cdot \dfrac 1<\sqrt3>a\]

Замечание

Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\) ).

Пример 3

Решение

Пример 4

Решение

\[\dfrac=\dfrac \Rightarrow DH=\dfrac<\sqrt6>3x \Rightarrow HK=\dfrac<\sqrt6>6x \Rightarrow DH:HK=2:1\]

Источник

Узнать ещё

Знание — сила. Познавательная информация

Как построить сечение пирамиды

Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.

В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.

Построить сечение плоскостью (MNP)

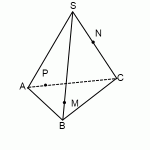
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Треугольник MNP — сечение пирамиды

Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.

Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.

Треугольник MNP — искомое сечение.

Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.

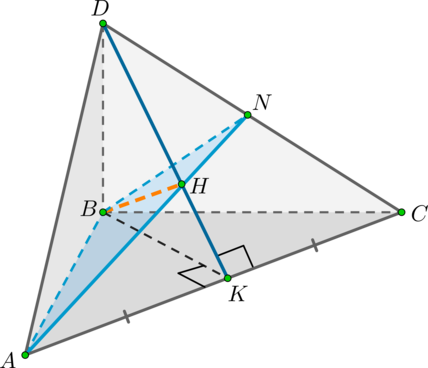
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.

Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.

Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.

Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.

Треугольник BKL — искомое сечение.

Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.

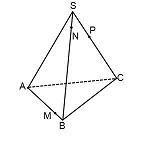
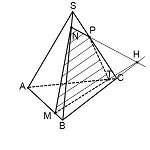
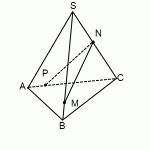
Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.

Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.

Продолжим прямую NP.

Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.

Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.

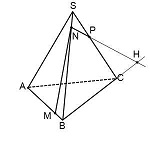
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.

Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).

Через H и точку M, лежащую в этой же плоскости, можем провести прямую.

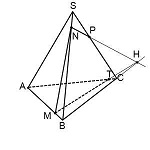
T — точка пересечения прямых MH и AC.

Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).

4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.

Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.

Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости. У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.

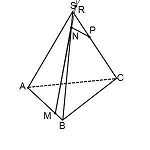
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.

Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), 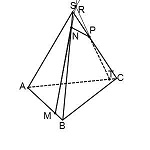которой принадлежит прямая AS.

Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.

Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.

Таким образом, получили все то же сечение MNPT.

Рассмотрим еще один пример такого рода.

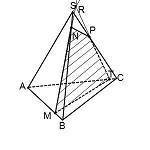
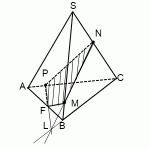
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).

Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).

Через точки M и P прямую провести не можем.

1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.

Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.

F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.

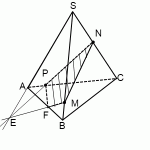
2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.

Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).

Источник