Как построить регрессию в питоне

Полное руководство по линейной регрессии в Python

Дата публикации Jun 18, 2019

Введение

Эта статья пытается быть справочной информацией, которая вам нужна, когда дело доходит до понимания и выполнения линейной регрессии. Хотя алгоритм прост, лишь немногие действительно понимают основные принципы.

Во-первых, мы углубимся в теорию линейной регрессии, чтобы понять ее внутреннюю работу. Затем мы реализуем алгоритм на Python для моделирования бизнес-задачи.

Я надеюсь, что эта статья найдет свой путь в ваши закладки! А пока давайте к этому!

Теория

Линейная регрессия, вероятно, является самым простым подходом для статистического обучения. Это хорошая отправная точка для более продвинутых подходов, и фактически многие причудливые статистические методы обучения можно рассматривать как расширение линейной регрессии. Следовательно, понимание этой простой модели создаст хорошую базу, прежде чем перейти к более сложным подходам.

Линейная регрессия очень хороша, чтобы ответить на следующие вопросы:

Оценка коэффициентов

Предположим, у нас есть только одна переменная и одна цель. Тогда линейная регрессия выражается как:

Итак, как мы можем найти эти параметры?

Чтобы найти параметры, нам нужно минимизироватьнаименьших квадратовилисумма квадратов ошибок, Конечно, линейная модель не идеальна, и она не будет точно предсказывать все данные, а это означает, что существует разница между фактическим значением и прогнозом. Ошибка легко вычисляется с помощью:

Но почему ошибки возводятся в квадрат?

Мы возводим в квадрат ошибку, потому что прогноз может быть выше или ниже истинного значения, что приводит к отрицательной или положительной разнице соответственно. Если бы мы не возводили в квадрат ошибки, сумма ошибок могла бы уменьшиться из-за отрицательных различий, а не потому, что модель хорошо подходит.

Кроме того, возведение в квадрат ошибок учитывает большие различия, поэтому минимизация квадратов ошибок «гарантирует» лучшую модель.

Давайте посмотрим на график, чтобы лучше понять.

После некоторой математики, которая является слишком тяжелой для этой статьи, вы можете наконец оценить коэффициенты с помощью следующих уравнений:

гдех бара такжеу барпредставляют собой среднее.

Оцените актуальность коэффициентов

Теперь, когда у вас есть коэффициенты, как вы можете определить, актуальны ли они для прогнозирования вашей цели?

Для любой задачи моделирования гипотеза состоит в том, чтоесть некоторая корреляциямежду функциями и целью. Таким образом, нулевая гипотеза противоположна:нет корреляциимежду функциями и целью.

Итак, нахождениер-значениедля каждого коэффициента будет указано, является ли переменная статистически значимой для прогнозирования цели. Как правило, еслир-значениеявляетсяменее чем 0,05: между переменной и целью существует тесная связь.

Оцените точность модели

Вы обнаружили, что ваша переменная была статистически значимой, найдя еер-значение, Большой!

Теперь, как узнать, хороша ли ваша линейная модель?

Чтобы оценить это, мы обычно используем RSE (остаточная стандартная ошибка) и статистику R².

Первая метрика ошибки проста для понимания: чем меньше остаточных ошибок, тем лучше модель соответствует данным (в этом случае, чем ближе данные к линейной зависимости).

Что касается метрики R², он измеряетдоля изменчивости в цели, которая может быть объяснена с помощью функции X, Следовательно, при условии линейного отношения, если признак X может объяснить (предсказать) цель, тогда пропорция высока, и значение R² будет близко к 1. Если противоположное верно, значение R² будет тогда ближе к 0.

Теория множественной линейной регрессии

В реальных ситуациях никогда не будет единственной функции, чтобы предсказать цель Итак, выполняем ли мы линейную регрессию по одному объекту за раз? Конечно нет. Мы просто выполняем множественную линейную регрессию.

Уравнение очень похоже на простую линейную регрессию; просто добавьте количество предикторов и соответствующие им коэффициенты:

Оцените актуальность предиктора

Ранее в простой линейной регрессии мы оценивали релевантность функции, находя еер-значение,

В случае множественной линейной регрессии мы используем другую метрику: F-статистику.

Здесь F-статистика рассчитывается для всей модели, тогда какр-значениеспецифичен для каждого предиктора. Если существует сильная связь, то F будет намного больше 1. В противном случае она будет приблизительно равна 1.

Какбольшечем 1достаточно большой?

Это сложно ответить. Обычно, если имеется большое количество точек данных, F может быть немного больше 1 и предполагать тесную связь. Для небольших наборов данных значение F должно быть намного больше 1, чтобы предполагать тесную связь.

Почему мы не можем использоватьр-значениев этом случае?

Поскольку мы подгоняем много предикторов, нам нужно рассмотреть случай, когда есть много функций (пбольшой). При очень большом количестве предикторов всегда будет около 5%, у которых, случайнор-значениечетное хотя они не являются статистически значимыми.Поэтому мы используем F-статистику, чтобы не рассматривать неважные предикторы как значимые предикторы.

Оцените точность модели

Как и в простой линейной регрессии, R² может использоваться для множественной линейной регрессии. Однако знайте, что добавление большего количества предикторов всегда будет увеличивать значение R², потому что модель обязательно будет лучше соответствовать обучающим данным.

Тем не менее, это не означает, что он будет хорошо работать с тестовыми данными (делая прогнозы для неизвестных точек данных).

Добавление взаимодействия

Наличие нескольких предикторов в линейной модели означает, что некоторые предикторы могут влиять на другие предикторы.

Например, вы хотите предсказать зарплату человека, зная его возраст и количество лет, проведенных в школе. Конечно, чем старше человек, тем больше времени он мог бы проводить в школе. Итак, как мы моделируем этот эффект взаимодействия?

Рассмотрим этот очень простой пример с двумя предикторами:

Как видите, мы просто умножаем оба предиктора вместе и связываем новый коэффициент. Упрощая формулу, мы теперь видим, что на коэффициент влияет значение другого признака.

Как правило, если мы включаем модель взаимодействия, мы должны включать индивидуальный эффект объекта, даже если егор-значениенезначительный. Это известно какиерархический принцип, Это объясняется тем, что если два предиктора взаимодействуют, то включение их индивидуального вклада окажет небольшое влияние на модель.

Хорошо! Теперь, когда мы знаем, как это работает, давайте заставим это работать! Мы будем работать как с простой, так и с множественной линейной регрессией в Python, и я покажу, как оценивать качество параметров и общую модель в обеих ситуациях.

Вы можете получить код и данныеВот,

Я настоятельно рекомендую вам следовать и воссоздать шаги в своем собственном блокноте Jupyter, чтобы в полной мере воспользоваться этим руководством.

Давайте доберемся до этого!

Мы все так кодируем, верно?

Введение

Набор данных содержит информацию о деньгах, потраченных на рекламу, и их продажах. Деньги были потрачены на рекламу на телевидении, радио и в газетах.

Цель состоит в том, чтобы использовать линейную регрессию, чтобы понять, как расходы на рекламу влияют на продажи.

Импорт библиотек

Преимущество работы с Python заключается в том, что у нас есть доступ ко многим библиотекам, которые позволяют нам быстро читать данные, наносить на график данные и выполнять линейную регрессию.

Мне нравится импортировать все необходимые библиотеки поверх ноутбука, чтобы все было организовано. Импортируйте следующее:

Читать данные

Предполагая, что вы загрузили набор данных, поместите его в data каталог в папке вашего проекта. Затем прочитайте данные так:

Чтобы увидеть, как выглядят данные, мы делаем следующее:

И вы должны увидеть это:

Как видите, столбец Unnamed: 0 избыточно Следовательно, мы удалим это.

Хорошо, наши данные чисты и готовы к линейной регрессии!

Простая линейная регрессия

моделирование

Для простой линейной регрессии, давайте рассмотрим только влияние телевизионной рекламы на продажи. Прежде чем перейти непосредственно к моделированию, давайте посмотрим, как выглядят данные.

Запустите эту ячейку кода, и вы должны увидеть этот график:

Как видите, существует четкая взаимосвязь между суммой, потраченной на телевизионную рекламу, и продажами.

Давайте посмотрим, как мы можем сгенерировать линейное приближение этих данных.

Да! Это так просто, чтобы подогнать прямую линию к набору данных и увидеть параметры уравнения. В этом случае мы имеем

Давайте представим, как линия соответствует данным.

И теперь вы видите:

Из приведенного выше графика видно, что простая линейная регрессия может объяснить общее влияние суммы, потраченной на телевизионную рекламу и продажи.

Оценка актуальности модели

Теперь, если вы помните из этогопосле, чтобы увидеть, является ли модель хорошей, нам нужно посмотреть на значение R² ир-значениеот каждого коэффициента.

Вот как мы это делаем:

Что дает вам этот прекрасный вывод:

Глядя на оба коэффициента, мы имеемр-значениеэто очень мало (хотя, вероятно, это не совсем 0). Это означает, что существует сильная корреляция между этими коэффициентами и целью (продажи).

Затем, глядя на значение R², мы получаем 0,612. Следовательно,около 60% изменчивости продаж объясняется суммой, потраченной на телевизионную рекламу, Это нормально, но точно не лучшее, что мы можем точно предсказать продажи. Конечно, расходы на рекламу в газетах и ​​на радио должны оказывать определенное влияние на продажи.

Посмотрим, будет ли лучше работать множественная линейная регрессия.

Множественная линейная регрессия

моделирование

Как и для простой линейной регрессии, мы определим наши функции и целевую переменную и используемscikit учитьсябиблиотека для выполнения линейной регрессии.

Больше ничего! Из этой ячейки кода мы получаем следующее уравнение:

Конечно, мы не можем визуализировать влияние всех трех сред на продажи, так как оно имеет четыре измерения.

Обратите внимание, что коэффициент для газеты является отрицательным, но также довольно небольшим. Это относится к нашей модели? Давайте посмотрим, рассчитав F-статистику, значение R² ир-значениеза каждый коэффициент.

Оценка актуальности модели

Как и следовало ожидать, процедура здесь очень похожа на то, что мы делали в простой линейной регрессии.

И вы получите следующее:

Как вы можете видеть, R² намного выше, чем у простой линейной регрессии, со значением0,897!

Кроме того, F-статистика570,3, Это намного больше, чем 1, и поскольку наш набор данных достаточно мал (всего 200 точек),демонстрирует тесную связь между расходами на рекламу и продажами,

Наконец, поскольку у нас есть только три предиктора, мы можем рассмотреть ихр-значениеопределить, имеют ли они отношение к модели или нет. Конечно, вы заметили, что третий коэффициент (для газеты) имеет большойр-значение, Поэтому рекламные расходы на газетуне является статистически значимым, Удаление этого предиктора немного уменьшит значение R², но мы могли бы сделать более точные прогнозы.

Вы качаетесь 🤘. Поздравляю с завершением, теперь вы мастер линейной регрессии!

Как упоминалось выше, это может быть не самый эффективный алгоритм, но он важен для понимания линейной регрессии, поскольку он формирует основу более сложных статистических подходов к обучению.

Я надеюсь, что вы когда-нибудь вернетесь к этой статье.

Источник

Линейная регрессия на Python: объясняем на пальцах

Линейная регрессия применяется для анализа данных и в машинном обучении. Постройте свою модель на Python и получите первые результаты!

Что такое регрессия?

Регрессия ищет отношения между переменными.

Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.

Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.

Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.

Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.

Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.

Зависимые данные называются зависимыми переменными, выходами или ответами.

Независимые данные называются независимыми переменными, входами или предсказателями.

Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.

Когда вам нужна регрессия?

Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.

Где она вообще нужна?

Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.

Линейная регрессия

Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.

Постановка проблемы

Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.

Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.

Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.

Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.

Простая линейная регрессия

Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.

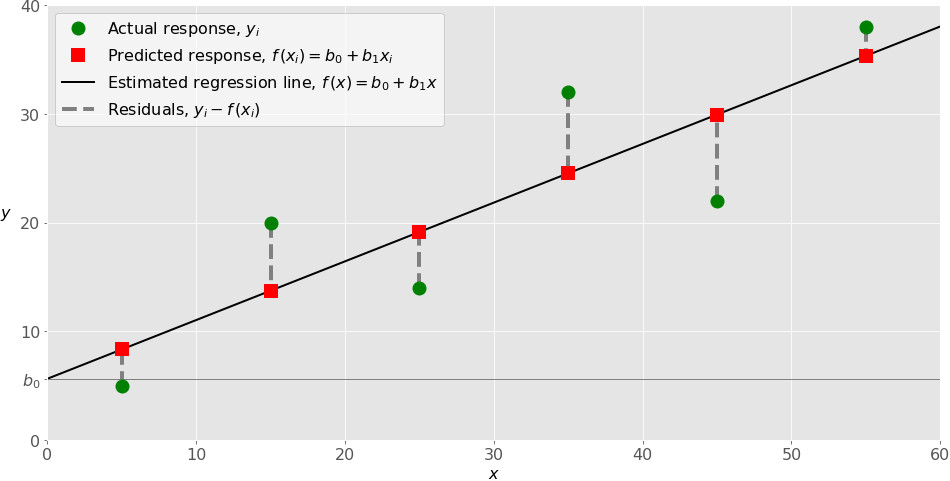
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.

Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.

Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).

Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.

Реализуйте линейную регрессию в Python

Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.

Пакеты Python для линейной регрессии

NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.

Незнакомы с NumPy? Начните с официального гайда.

Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.

Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.

Простая линейная регрессия со scikit-learn

Начнём с простейшего случая линейной регрессии.

Следуйте пяти шагам реализации линейной регрессии:

Это общие шаги для большинства подходов и реализаций регрессии.

Шаг 1: Импортируйте пакеты и классы

Первым шагом импортируем пакет NumPy и класс LinearRegression из sklearn.linear_model :

Теперь у вас есть весь функционал для реализации линейной регрессии.

Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.

Шаг 2 : Предоставьте данные

Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, x) и выход (предиктор, y) должны быть массивами (экземпляры класса numpy.ndarray ) или похожими объектами. Вот простейший способ предоставления данных регрессии:

Вот как x и y выглядят теперь:

Шаг 3: Создайте модель

На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.

Наш пример использует состояния параметров по умолчанию.

Эта операция короче и делает то же, что и две предыдущие.

Шаг 4: Получите результаты

После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.

.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².

Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.

Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:

Шаг 5: Предскажите ответ

Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.

Вот почти идентичный способ предсказать ответ:

В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.

Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.

На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:

О LinearRegression вы узнаете больше из официальной документации.

Теперь у вас есть своя модель линейной регрессии!

Источник

Python, корреляция и регрессия: часть 1

Чем больше я узнаю людей, тем больше мне нравится моя собака.

В этой серии постов будет рассмотрена линейная регрессия. При наличии выборки данных наша модель усвоит линейное уравнение, позволяющее ей делать предсказания о новых, не встречавшихся ранее данных. Для этого мы снова обратимся к библиотеке pandas и изучим связь между ростом и весом спортсменов-олимпийцев. Мы введем понятие матриц и покажем способы управления ими с использованием библиотеки pandas.

О данных

В этой серии постов используются данные, любезно предоставленные компанией Guardian News and Media Ltd., о спортсменах, принимавших участие в Олимпийских Играх 2012 г. в Лондоне. Эти данные изначально были взяты из блога газеты Гардиан.

Обследование данных

Когда вы сталкиваетесь с новым набором данных, первая задача состоит в том, чтобы его обследовать с целью понять, что именно он содержит.

Файл all-london-2012-athletes.tsv достаточно небольшой. Мы можем обследовать данные при помощи pandas, как мы делали в первой серии постов «Python, исследование данных и выборы», воспользовавшись функцией read_csv :

Если выполнить этот пример в консоли интерпретатора Python либо в блокноте Jupyter, то вы должны увидеть следующий ниже результат:

Столбцы данных (нам повезло, что они ясно озаглавлены) содержат следующую информацию:

страна, за которую он выступает

дата рождения в виде строки

место рождения в виде строки (со страной)

число выигранных золотых медалей

число выигранных серебряных медалей

число выигранных бронзовых медалей

всего выигранных золотых, серебряных и бронзовых медалей

вид спорта, в котором он соревновался

состязание в виде списка, разделенного запятыми

Даже с учетом того, что данные четко озаглавлены, очевидно присутствие пустых мест в столбцах с ростом, весом и местом рождения. При наличии таких данных следует проявлять осторожность, чтобы они не сбили с толку.

Визуализация данных

В первую очередь мы рассмотрим разброс роста спортсменов на Олимпийских играх 2012 г. в Лондоне. Изобразим эти значения роста в виде гистограммы, чтобы увидеть характер распределения данных, не забыв сначала отфильтровать пропущенные значения:

Этот пример сгенерирует следующую ниже гистограмму:

Как мы и ожидали, данные приближенно нормально распределены. Средний рост спортсменов составляет примерно 177 см. Теперь посмотрим на распределение веса олимпийских спортсменов:

Приведенный выше пример сгенерирует следующую ниже гистограмму:

К счастью, эта асимметрия может быть эффективным образом смягчена путем взятия логарифма веса при помощи функции библиотеки numpy np.log :

Этот пример сгенерирует следующую ниже гистограмму:

Теперь данные намного ближе к нормальному распределению. Из этого следует, что вес распределяется согласно логнормальному распределению.

Логнормальное распределение

Логнормальное распределение — это распределение набора значений, чей логарифм нормально распределен. Основание логарифма может быть любым положительным числом за исключением единицы. Как и нормальное распределение, логнормальное распределение играет важную роль для описания многих естественных явлений.

Логарифм показывает степень, в которую должно быть возведено фиксированное число (основание) для получения данного числа. Изобразив логарифмы на графике в виде гистограммы, мы показали, что эти степени приближенно нормально распределены. Логарифмы обычно берутся по основанию 10 или основанию e, трансцендентному числу, приближенно равному 2.718. В функции библиотеки numpy np.log и ее инверсии np.exp используется основание e. Выражение log_e также называется натуральным логарифмом, или ln, из-за свойств, делающих его особенно удобным в исчислении.

Логнормальное распределение обычно имеет место в процессах роста, где темп роста не зависит от размера. Этот феномен известен как закон Джибрэта, который был cформулирован в 1931 г. Робертом Джибрэтом, заметившим, что он применим к росту фирм. Поскольку темп роста пропорционален размеру, более крупные фирмы демонстрируют тенденцию расти быстрее, чем фирмы меньшего размера.

Нормальное распределение случается в ситуациях, где много мелких колебаний, или вариаций, носит суммирующий эффект, тогда как логнормальное распределение происходит там, где много мелких вариаций имеет мультипликативный эффект.

С тех пор выяснилось, что закон Джибрэта применим к большому числу ситуаций, включая размеры городов и, согласно обширному математическому ресурсу Wolfram MathWorld, к количеству слов в предложениях шотландского писателя Джорджа Бернарда Шоу.

В остальной части этой серии постов мы будем использовать натуральный логарифм веса спортсменов, чтобы наши данные были приближенно нормально распределены. Мы выберем популяцию спортсменов примерно с одинаковыми типами телосложения, к примеру, олимпийских пловцов.

Визуализация корреляции

Один из самых быстрых и самых простых способов определить наличие корреляции между двумя переменными состоит в том, чтобы рассмотреть их на графике рассеяния. Мы отфильтруем данные, выбрав только пловцов, и затем построим график роста относительно веса спортсменов:

Этот пример сгенерирует следующий ниже график:

Результат ясно показывает, что между этими двумя переменными имеется связь. График имеет характерно смещенную эллиптическую форму двух коррелируемых, нормально распределенных переменных с центром вокруг среднего значения. Следующая ниже диаграмма сравнивает график рассеяния с распределениями вероятностей роста и логарифма веса:

Точки, близко расположенные к хвосту одного распределения, также демонстрируют тенденцию близко располагаться к тому же хвосту другого распределения, и наоборот. Таким образом, между двумя распределениями существует связь, которую в ближайших нескольких разделах мы покажем, как определять количественно. Впрочем, если мы внимательно посмотрим на предыдущий график рассеяния, то увидим, что из-за округления измерений точки уложены в столбцы и строки (в см. и кг. соответственно для роста и веса). Там, где это происходит, иногда желательно внести в данные искажения, которые также называются сдвигом или джиттером с тем, чтобы яснее показать силу связи. Без генерирования джиттера (в виде случайных отклонений) может оказаться, что, то, что по внешнему виду составляет одну точку, фактически представляет много точек, которые обозначены одинаковой парой значений. Внесение нескольких случайных помех делает эту ситуацию вряд ли возможной.

Генерирование джиттера

График с джиттером выглядит следующим образом:

Как и в случае с внесением прозрачности в график рассеяния в первой серии постов об описательной статистике, генерирование джиттера — это механизм, который обеспечивает исключение несущественных факторов, таких как объем данных или артефакты округления, которые могут заслонить от нас возможность увидеть закономерности в данных.

Ковариация

Одним из способов количественного определения силы связи между двумя переменными является их ковариация. Она измеряет тенденцию двух переменных изменяться вместе.

Если у нас имеется два ряда чисел, X и Y, то их отклонения от среднего значения составляют:

Здесь x_i — это значение X с индексом i, y_i — значение Y с индексом i, x̅ — среднее значение X, и y̅ — среднее значение Y. Если X и Y проявляют тенденцию изменяться вместе, то их отклонения от среднего будет иметь одинаковый знак: отрицательный, если они — меньше среднего, положительный, если они больше среднего. Если мы их перемножим, то произведение будет положительным, когда у них одинаковый знак, и отрицательным, когда у них разные знаки. Сложение произведений дает меру тенденции этих двух переменных отклоняться от среднего значения в одинаковом направлении для каждой заданной выборки.

Ковариация определяется как среднее этих произведений:

На чистом Python ковариация вычисляется следующим образом:

В качестве альтернативы, мы можем воспользоваться функцией pandas cov :

Ковариация роста и логарифма веса для наших олимпийских пловцов равна 1.356, однако это число сложно интерпретировать. Единицы измерения здесь представлены произведением единиц на входе.

Стандартная оценка, англ. standard score, также z-оценка — это относительное число стандартных отклонений, на которые значение переменной отстоит от среднего значения. Положительная оценка показывает, что переменная находится выше среднего, отрицательная — ниже среднего. Это безразмерная величина, получаемая при вычитании популяционного среднего из индивидуальных значений и деления разности на популяционное стандартное отклонение.

Корреляция Пирсона

Корреляция Пирсона часто обозначается переменной r и вычисляется следующим образом, где отклонения от среднего dx_i и dy_i вычисляются как и прежде:

Поскольку для переменных X и Y стандартные отклонения являются константными, уравнение может быть упрощено до следующего, где σ_x и σ_y — это стандартные отклонения соответственно X и Y:

В таком виде формула иногда упоминается как коэффициент корреляции смешанных моментов Пирсона или попросту коэффициент корреляции и, как правило, обозначается буквой r.

Ранее мы уже написали функции для вычисления стандартного отклонения. В сочетании с нашей функцией с вычислением ковариации получится следующая ниже имплементация корреляции Пирсона:

В качестве альтернативы мы можем воспользоваться функцией pandas corr :

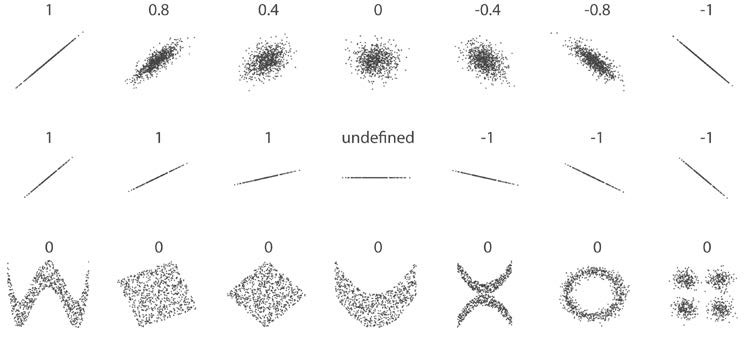
Правда, если r = 0, то с необходимостью вовсе не следует, что переменные не коррелируют. Корреляция Пирсона измеряет лишь линейные связи. Как продемонстрировано на следующих графиках, между переменными может существовать еще некая нелинейная связь, которую r не объясняет:

Отметим, что корреляция центрального примера не определена, потому что стандартное отклонение y = 0. Поскольку наше уравнение для r содержало бы деление ковариации на 0, то результат получается бессмысленным. В этом случае между переменными не может быть никакой корреляции; y всегда будет иметь среднее значение. Простое обследование стандартных отклонений это подтвердит.

Мы можем вычислить коэффициент корреляции для данных роста и логарифма веса наших пловцов следующим образом:

В результате получим ответ 0.867, который количественно выражает сильную, положительную корреляцию, уже наблюдавшуюся нами на точечном графике.

Выборочный r и популяционный ρ

Аналогично среднему значению и стандартному отклонению, коэффициент корреляции является сводной статистикой. Он описывает выборку; в данном случае, выборку спаренных значений: роста и веса. Коэффициент корреляции известной выборки обозначается буквой r, тогда как коэффициент корреляции неизвестной популяции обозначается греческой буквой ρ (рхо).

Как мы убедились в предыдущей серии постов о тестировании гипотез, мы не должны исходить из того, что результаты, полученные в ходе измерения нашей выборки, применимы к популяции в целом. К примеру, наша популяция может состоять из всех пловцов всех недавних Олимпийских игр. И будет совершенно недопустимо обобщать, например, на другие олимпийские виды спорта, такие как тяжелая атлетика или фитнес-плавание.

Даже в допустимой популяции — такой как пловцы, выступавшие на недавних Олимпийских играх, — наша выборка коэффициента корреляции является всего лишь одной из многих потенциально возможных. То, насколько мы можем доверять нашему r, как оценке параметра ρ, зависит от двух факторов:

Проверка статистических гипотез

В предыдущей серии постов мы познакомились с проверкой статистических гипотез, как средством количественной оценки вероятности, что конкретная гипотеза (как, например, что две выборки взяты из одной и той же популяции) истинная. Чтобы количественно оценить вероятность, что корреляция существует в более широкой популяции, мы воспользуемся той же самой процедурой.

В первую очередь, мы должны сформулировать две гипотезы, нулевую гипотезу и альтернативную:

Стандартная ошибка коэффициента корреляции r по выборке задается следующей формулой:

Эта формула точна, только когда r находится близко к нулю (напомним, что величина ρ влияет на нашу уверенность), но к счастью, это именно то, что мы допускаем согласно нашей нулевой гипотезы.

Мы можем снова воспользоваться t-распределением и вычислить t-статистику:

P-значение настолько мало, что в сущности равно 0, означая, что шанс, что нулевая гипотеза является истинной, фактически не существует. Мы вынуждены принять альтернативную гипотезу о существовании корреляции.

Интервалы уверенности

Установив, что в более широкой популяции, безусловно, существует корреляция, мы, возможно, захотим количественно выразить диапазон значений, внутри которого, как мы ожидаем, будет лежать параметр ρ, вычислив для этого интервал уверенности. Как и в случае со средним значением в предыдущей серии постов, интервал уверенности для r выражает вероятность (выраженную в %), что параметр ρ популяции находится между двумя конкретными значениями.

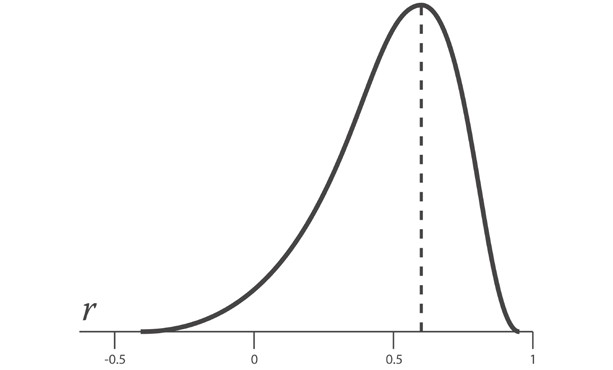
Однако при попытке вычислить стандартную ошибку коэффициента корреляции возникает сложность, которой не было в случае со средним значением. Поскольку абсолютное значение коэффициента корреляции r не может превышать 1, распределение возможных выборок коэффициентов корреляции r смещается по мере приближения r к пределу своего диапазона.

Приведенный выше график показывает отрицательно скошенное распределение r-выборок для параметра ρ, равного 0.6.

К счастью, трансформация под названием z-преобразование Фишера стабилизирует дисперсию r по своему диапазону. Она аналогична тому, как наши данные о весе спортсменов стали нормально распределенными, когда мы взяли их логарифм.

Уравнение для z-преобразования следующее:

Стандартная ошибка z равна:

Таким образом, процедура вычисления интервалов уверенности состоит в преобразовании r в z с использованием z-преобразования, вычислении интервала уверенности в терминах стандартной ошибки SE_z и затем преобразовании интервала уверенности в r.

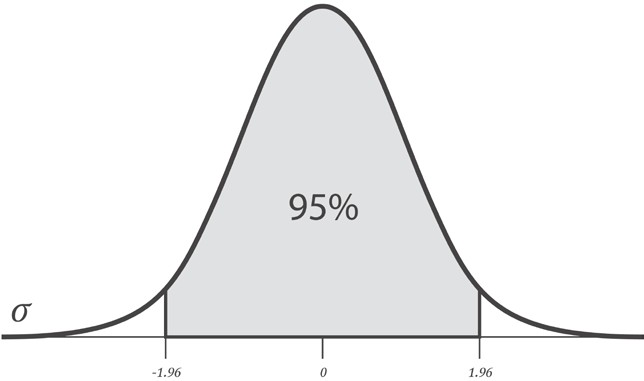
В целях вычисления интервала уверенности в терминах SE_z, мы можем взять число стандартных отклонений от среднего, которое дает нам требуемый уровень доверия. Обычно используют число 1.96, так как оно является числом стандартных отклонений от среднего, которое содержит 95% площади под кривой. Другими словами, 1.96 стандартных ошибок от среднего значения выборочного r содержит истинную популяционную корреляцию ρ с 95%-ой определенностью.

Однако, как показано на приведенном выше графике, мы хотели бы вычесть ту же самую величину, т.е. 2.5%, из каждого хвоста с тем, чтобы 95%-й интервал уверенности был центрирован на нуле. Для этого при выполнении двусторонней проверки нужно просто уменьшить разность наполовину и вычесть результат из 100%. Так что, требуемый уровень доверия в 95% означает, что мы обращаемся к критическому значению 97.5%:

Поэтому наш 95%-й интервал уверенности в z-пространстве для ρ задается следующей формулой:

Для r=0.867 и n=859 она даст нижнюю и верхнюю границу соответственно 1.137 и 1.722. В целях их преобразования из z-оценок в r-значения, мы используем следующее обратное уравнение z-преобразования:

Преобразования и интервал уверенности можно вычислить при помощи следующего исходного кода:

В результате получаем 95%-й интервал уверенности для ρ, расположенный между 0.850 и 0.883. Мы можем быть абсолютно уверены в том, что в более широкой популяции олимпийских пловцов существует сильная положительная корреляция между ростом и весом.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

Источник