Как построить развертку усеченной пирамиды
Правильная пятиугольная пирамида. Развертка усеченной пирамиды.
Правильная пятиугольная пирамида. Развертка усеченной пирамиды.
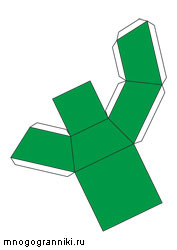
Правильная пирамида, в основании которой лежит правильный пятиугольник, усеченная плоскостью, показана на рис. 1.
Рис. 1. Развертка правильного пятиугольника усеченного плоскостью.
Как построить сечение пятиугольной пирамиды?!
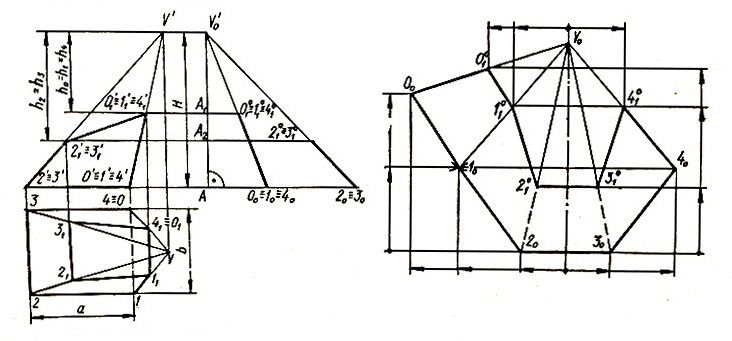
Через точки 3′, 3″ и 0′, 0″ проводятся прямые до пересечения в точке V’, являющейся вершиной пирамиды. Откладывается расстояние М’0′0 = М0. Точки 0’0 и V’ соединяются. Через точки пересечения ребер с плоскостью 0″, 1″, …, 5″ проводятся горизонтальные прямые до пересечения с прямой 0’0V’ в точках 0″0, 1″0, …, 5″0. Расстояние 0’0V’ = L определяет действительную длину ребра пирамиды.
Развертка строится следующим образом. Выбирается произвольный центр V0.
Из него радиусом, равным длине бокового ребра пирамиды R = L, описывается дуга. От произвольной точки 00 на дуге как хорда пять раз последовательно откладывается сторона основания а. Полученные точки 00, 10, …, 50 соединяются последовательно между собой и с вершиной V0. Из вершины откладываются расстояния V00″0 = V’0″0, V01″0 = V’1″0 и т. д. Полученные точки соединяются.
Для построения верхнего основания проводятся перпендикуляры к отрезку 0″3″ из точек 0″, 1″, 4″, 2″, 3″. После выбора произвольной точки 01 на перпендикуляре из точки 0″ из центра 01 радиусом 0″01″0 развертки описывается, дуга до пересечения с перпендикуляром в точке 11. Из центра 11 радиусом 1″02″0 описывается дуга до пересечения, перпендикуляра, проходящего через точку 2″, в точке 21. Построение продолжается при сохранении выбранного направления до замыкания многоугольника. Полученный многоугольник 011141 присоединяется к какому-либо из ребер развертки или выполняется отдельно.
Усеченная четырехугольная пирамида
Популярное
Памятник многограннику «Усечённый большой додекаэдр» был обнаружен в городе Обнинск, напротив здания «ДОСААФ» (ул.Шацкого, д.14).
Достаточно часто возникает вопрос о практическом применении бумажных развёрток. Какой смысл в бумажном моделировании?
Знакомые каждому с детства коробочки для Биг-Мака и картошки, стаканчик для Кока-Колы так же делают из бумажных разверток.
Существует концепция, что вершина многогранника отдает энергию, а плоскость энергию принимает. В том случае, если в многограннике вершин больше чем плоскостей, то он обладает.
Обработка металла это очень сложный технологический процесс. Но существуют мастера, кто умеет вытачивать многогранники из металла внутри другого.
Сюжет фантастического блокбастера «Пятый элемент», построен на легенде, что существуют пять элементов, которые способны защитить мир от угрозы Абсолютного Зла.
Ключевым элементом этого проекта является правильная треугольная призма.
Усеченная пятиугольная пирамида
данную пирамиду можно вписать в усечённый конус с радиусами оснований r=35 мм и R=55 мм
данную пирамиду можно вписать в усечённый конус с радиусами оснований r=25 мм и R=50 мм
данную пирамиду можно вписать в усечённый конус с радиусами оснований r=20 мм и R=50 мм
Популярное
Интересный лайфхак, прислала наша читательница из Республики Беларусь.
Для Вашего удобства мы снизили стоимость доставки наборов «Волшебные грани» в разы!
Нам нужны еще фонарики Джека в форме тыквы. Кто же нам поможет? Может быть Архимед?
Это небольшая «шуточная» задача поможет Вам на некоторое время занять ваших детей! Какой пластиковый тетраэдр* нужно расплавить, чтобы из.
Обработка металла это очень сложный технологический процесс. Но существуют мастера, кто умеет вытачивать многогранники из металла внутри другого.
Эта модель многогранника представляет из себя пересечение трёх параллелепипедов. В её основе пересечение трёх прямоугольников, где.
Наклонная пирамида развертка. Усеченная четырехгранная пирамида.
Наклонная пирамида развертка. Усеченная четырехгранная пирамида.
Наклонная усеченная пирамида с четырехугольным основанием показана на рис. 1.
Через точки 0′, 0′1 и 2′, 2′1 проводятся прямые до пересечения в точке V’, являющейся вершиной пирамиды.
Рис. 1.
Для определения действительном длины ребер пирамиды через произвольную точку А проводят две перпендикулярные прямые. На горизонтальной линии от точки А откладываются расстояния V0, V1,…,V4 до точек 00, 10, 20,…,40. На вертикальной линии откладывается высота пирамиды Н до точки V’0. Расстояния 00V’0, 10V’0,…, 40V’0 представляют собой действительные длины ребер. Для построения развертки необходимо из произвольной точки V0 отложить отрезок V000 = V’000. Из центров V0 и 00 радиусами соответственно V010 = V’010 и 0010 = 01 описываются дуги до пересечения в точке 10. Из центров V0 и 00 описываются дуги радиусами V020 = V’020 и 1020 = 12 до пересечения в точке 20. Построение продолжается по описанному способу до получения точки 40. Точки 10, 20, 30 и 40 последовательно соединяются между собой и каждая с V0.
Развертка усеченной пирамиды четырехугольной.
Действительная длина ребер малого основания определяется следующим образом. От точки V’0 откладываются расстояния h0 = h1 = h4 до точки А1 и h2 = h3 до точки А2. Через точки А1 и А2 проводятся горизонтальные прямые до пересечения V’000 и V’020 в точках 0 0 1 = 1 0 1 = 4 0 1 и 2 0 1 = 3 0 1. Из центра V0 радиусом V’00 0 1 описывается дуга до пересечения V000, V010 и V040 соответственно в точках 0 0 1, 1 0 1 и 4 0 1. Радиусом V’02 0 1 из центра V0 описывается дуга до пересечения V020 и V030 в точках 2 0 1 и 3 0 1, Полученные точки 0 0 1, 1 0 1, 4 0 1 последовательно соединяются, расстояния 0 0 11 0 1, 1 0 12 0 1 являются действительными длинами ребер малого основания.
Инженерная графика. Проекция усеченной пирамиды
Описание презентации по отдельным слайдам:
Пересечение поверхностей геометрических тел Графическая работа №7 Вычертить комплексный чертеж усеченного гранного тела, развертку поверхности, аксонометрическую проекцию
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1551654
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
АСИ организует конкурс лучших управленческих практик в сфере детского образования
Время чтения: 2 минуты
Большинство родителей в России удовлетворены качеством образования в детсадах
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минздрав включил вакцинацию подростков от ковида в календарь прививок
Время чтения: 1 минута
Московские школьники победили на международной олимпиаде по информатике
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.