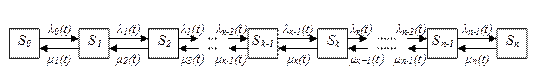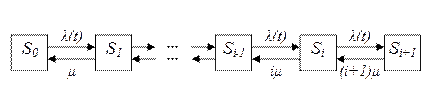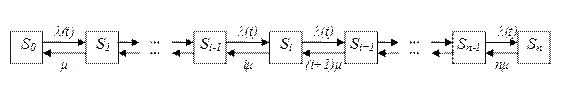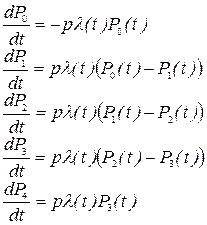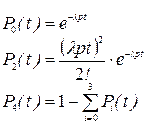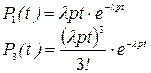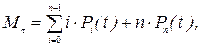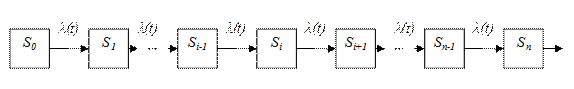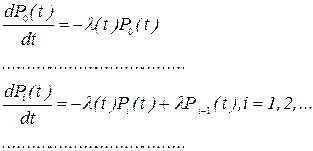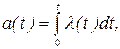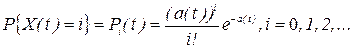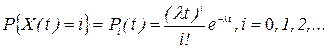Как построить размеченный граф состояний

Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний

Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, нам удобно будет представлять себе, что все переходы системы S из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, поток отказов, поток восстановлений и т.д.). Если все потоки событий, переводящие систему S из состояния в состояние,- простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем «будущее» не зависит от «прошлого».

Если система S находится в каком-то состоянии Si, из которого есть непосредственный переход в другое состояние Sj (стрелка, ведущая из Si в Sj на графе состояний), то мы себе это будем представлять так, как будто на систему, пока она находится в состоянии Si действует простейший поток событий, переводящий ее по стрелке Si → Sj. Как только появится первое событие этого потока, происходит «перескок» системы из Si в Sj.

Для наглядности очень удобно на графе состояний у каждой стрелки проставлять интенсивность того потока событий, который переводит систему по данной стрелке. Обозначим λij интенсивность потока событий, переводящего систему из состояния Si в Sj. На рис. 4.7 дан граф состояний с проставленными у стрелок интенсивностями (мы будем называть такой граф размеченным).

Рис. 4.7. Размеченный граф состояний

Построим размеченный граф состояний для технического устройства из двух узлов. Состояния системы:

Интенсивности потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу. Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии S0. Какой поток событий переводит ее в состояние S1? Очевидно, поток отказов первого узла. Его интенсивность λ1 равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из S1 в S0? Очевидно, поток «окончаний ремонтов» первого узла. Его интенсивность μ1 равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 4.7.

Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.

В самом деле, пусть рассматривается система S, имеющая n возможных состояний S1, S2. Sn. Назовем вероятностью i-го состояния вероятность pi(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:

Источник

Уравнения Колмогорова.
Предельные вероятности состояний

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.

Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).

Применяя теорему сложения вероятностей, получим

Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:

Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).

Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.

Процесс гибели и размножения

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.

По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие

Решая систему (14), (15), можно получить

Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.

Источник

Граф состояний системы

Восстанавливаемая система, состоящая из элементов, может находиться в большом числе состояний. Например, один элемент системы отказал, а остальные ( ) элемента работоспособны, или элементов отказали, а остальные ( ) работоспособны и т.п. В процессе эксплуатации из-за отказов и восстановлений система может неоднократно переходить из одного состояния в другое. Функционирование такой системы может быть описано так называемым графом состояний, узлами которого являются состояния системы, а ветвями – возможные переходы из состояния в состояния. Как правило, узлы графа в случае работоспособного состояния системы обозначаются в виде окружностей, а в случае отказового – квадратов. Если оценка функционирования системы осуществляется до некоторого i-го состояния, например до первого её отказа, то i-е состояние считается поглощающим. Система, попавшая в i-e состояние, уже не может перейти в другое, и в графе отсутствуют ветви переходов из этого состояния.

Рис. 6.1 Структурная схема нерезервированной восстанавливаемой системы

Рис. 6.2 Граф состояний нерезервированной восстанавливаемой системы

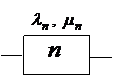В случае отказа i-го элемента системы, согласно графу состояний, происходит переход из работоспособного состояния (0), в неработоспособное i-ое состояние с интенсивностью отказов . В свою очередь i-ый элемент системы может быть восстановлен (система возвращена в состояние (0)) с интенсивностью .

В данном примере интенсивности переходов не зависят от числа обслуживающих бригад, т. к. предполагается, что после возникновения отказа одного элемента вся система не работает и отказы элементов в процессе ее восстановления не возникают.

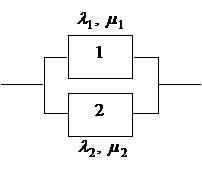
Пример. Структурная схема восстанавливаемой системы с постоянно включенным резервом представлена на рис. 6.3. Необходимо построить графы состояний данной системы для ряда случаев.

Рис. 6.3 Структурная схема восстанавливаемой системы с постоянно включенным резервом

Случай обслуживания системы двумя бригадами. Граф состояний системы для данного случая показан на рис.6.4, где (0) –состояние системы, при котором оба элемента работоспособны; (1) – состояние системы, при котором первый элемент отказал и находится в ремонте, а второй работоспособен; (2) – состояние системы, при котором первый элемент работоспособен, а второй отказал и находится в ремонте; (3) – отказовое состояние системы, при котором оба элемента неработоспособны и находится в ремонте.

Из исходного работоспособного состояния системы (0) возможны переходы в состояние (1) с интенсивностью и в состояние (2) с интенсивностью . После восстановления элемента система может вернуться из состояний (1) или (2) в работоспособное состояние (0). Возможна ситуация, когда до момента восстановления одного отказавшего элемента откажет и другой, тогда система перейдет в неработоспособное состояние (3) с интенсивностью из состояния (1) и из состояния (2). Так как система обслуживается двумя бригадами, то в состоянии (3) оба элемента ремонтируются одновременно независимо от того, какой из них отказал первым. В случае, когда в состоянии (3) пер­воначально будет отремонтирован первый элемент система перейдет с интенсивностью в состояние (2), а если второй –- то с интенсивностью в состояние (1).

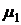
Случай обслуживания системы одной бригадой с прямым приоритетом. Граф состояний такой системы показан на рис. 6.5.

Рис. 6.5 Граф состояний восстанавливаемой системы с постоянно включенным резервом для случая обслуживания одной бригадой с прямым приоритетом

В данном случае восстановление отказавших элементов осуществляется одной обслуживающей бригадой. При таком обслуживании системы в неработоспособном состоянии ремонтируется только один элемент, а второй находится в очереди на ремонт. Следовательно, исследуемая система имеет два отказовых состояния (3) и (4). Так как рассматривается случай с прямым приоритетом обслуживания, в первую очередь осуществляется ремонт того элемента, который отказал первым. То есть, в случае перехода в неработоспособное состояние системы (3) ремонтируется первый элемент и система с интенсивностью 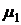переходит в состояние (2) – работоспособности первого элемента и неработоспособности второго, в случае перехода системы в состояние (4) ремонтируется второй элемент и система с интенсивностью переходит в состояние (1) – работоспособности второго и неработоспособности первого элементов.

Случай обслуживания системы одной бригадой с обратным приоритетом. Граф состояний системы для данного случая обслуживания показан на рис. 6.6.

Рис.6.6 Граф состояний восстанавливаемой системы с постоянно включенным резервом для случая обслуживания одной бригадой с обратным приоритетом

При обслуживании системы с обратным приоритетом, в первую очередь осуществляется ремонт последнего отказавшего элемента. В такой системе в случае её перехода в неработоспособное состояние (3) ремонтируется второй элемент и система с интенсивностью переходит в состояние (1), в случае перехода системы в состояние (4) ремонтируется первый элемент и система с интенсивностью переходит в состояние (2).

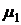
Случай обслуживания системы одной бригадой, причем первый элемент имеет высший приоритет по сравнению со вторым. Граф состояний такой системы показан на рис. 6.7.

Рис. 6.7 Граф состояний восстанавливаемой системы с постоянно включенным резервом для случая обслуживания одной бригадой с наивысшим приоритетом первого элемента

В данном случае первый элемент имеет приоритет при обслуживании, поэтому в неработоспособных состояниях (3) и (4) он восстанавливается первым. Таким образом, в случае перехода системы в одно из неработоспособных состояний (3) или (4) всегда ремонтируется первый элемент и система с интенсивностью 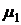всегда переходит в состояние (2).

Из примера следует, что вид графа состояний зависит не только от структуры системы, но также от числа обслуживающих бригад и дисциплины обслуживания.

При анализе надежности сложных систем имеющих большое число элементов приходится просматривать множество возможных состояний системы. При этом имеет место формализация графа состояний.

Согласно формализованному способу построения, граф состояний системы состоит из совокупности уровней, каждый из которых содержит набор возможных состояний системы при отказе i-го количества элементов. То есть, при i=0 (нулевой уровень) все элементы работоспособны, при i=1 (первый уровень) один из элементов отказал, а остальные работоспособны, при i=2 (второй уровень) два любых элемента отказали, а ос­тальные работоспособны и т. д. Последний уровень графа должен полностью состоять из набора неработоспособных состояний системы.

Пример. Структурная схема системы представлена на рис. 6.8.

Необходимо построить граф состояний такой системы, предполагая, что поток отказов системы является простейшим, т.е. обладает свойствами стационарности, ординарности и отсутствия последствий. Для системы установлен прямой приоритет обслуживания.

Граф состояний системы приведён на рис. 6.9.

Рис. 6.9 Граф состояний системы, изображённой на рис. 6.8

Граф состояний системы имеет четыре уровня. На нулевом уровне находится состояние (0), которое соответствует работоспособности всех элементов системы. Из состояния (0) система может пе­рейти в состояния, когда отказал один из её элементов. Данные состояния показаны на линии первого уровня цифрами 1, 2, 3, 4 в соответствии с отказавшими элементами системы. На этой линии узел с номером 5 отсутствует, так как находится в ненагруженном резерве и будет работать только в случае отказа элемента 4. Отказ 3-го элемента приводит к отказу всей системы, в связи с чем, данный узел обозначен квадратом и из него отсутствуют переходы на узлы второго уровня. На линии второго уровня находится состояния системы соответствующие неработоспособному состоянию любых двух её элементов. Например, из состояния (1) первого уровня возможны переходы в состояния, когда вслед за отказом элемента 1 отказывает либо элемент 2, либо элемент 3, либо элемент 4. Эти состояния обозначены (1,2), (1,3) и (1,4). Из состояний (1,2) и (1,3) отсутствуют переходы в состояния третьего уровня, так как они соответствуют неработоспособному состоянию системы. В состоянии (1,4) система работоспособна, поэтому из данного состояния возможны переходы в состояния третьего уровня. Так вслед за отказами элементов 1 и 4 могут отказать элементы либо 2, либо 3, либо 5. Соответствующие состояния расположены на линии третьего уровня и обозначены (1,4,2), (1,4,3), (1,4,5). Данный уровень графа состояния будет последним, так как все его состояния приводят к неработоспособности системы. Остальные ветви перехода соответствующие отказам элементов строится аналогично.

После обозначения на графе состояний, переходов соответствующих отказам элементов ( -переходы), необходимо показать ветви соответствующие восстановлению отказавших элементов ( -переходы). Например, в случае прямого приоритета обслуживания, в состоянии третьего уровня (1,4,3) первым будет восстановлен элемент 1 и система с интенсивностью перейдет в состояние (4,3) второго уровня. В состоянии (4,3) система будет неработоспособной, поэтому, во время ремонта элемента 4, новых отказов не произойдёт. После восстановления элемента 4 система перейдет с интенсив­ностью в состояние (3) первого уровня и затем с интенсивностью в состояние (0) нулевого уровня. Остальные ветви соответствующие -переходам строятся аналогично.

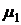
Описание функционирования системы с помощью графа состояний позволяет определить все количественные характеристики надежно­сти восстанавливаемой системы.

Источник

Процесс гибели и размножения

Название взято из биологических задач, где состояние популяции S_k означает наличие в ней k единиц особей.

Рис. 3.7. Граф состояний для процесса гибели и размножения

У l и μ индекс того состояния, из которою стрелка выходит.

С состоянием S_k связана неслучайная величина Х_k: если система S в момент времени t находится в состоянии S_k, то дискретная случайная величина X(t), связанная с функционированием системы, принимает значение k. Таким образом, получаем случайный процесс Х(t), который в случайные, заранее неизвестные моменты времени скачком изменяет свое состояние.

Марковским процессом гибели и размножения с непрерывным временем называется такой случайный процесс, который может принимать только целые неотрицательные значения. Изменения этого процесса могут происходить в любой момент времени, т. е. в любой момент времени он может либо увеличиться на единицу, либо уменьшиться на единицу, либо остаться неизменным.

В практике встречаются процессы чистого размножения и чистой гибели. Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю; аналогично процессом чистой «гибели» называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю.

1. Случайный процесс эксплуатации автомобилей есть процесс гибели и размножения, размеченный граф которого представлен на рис. 3.8.

Рис. 3.8. Граф состояний

Система уравнений Колмогорова, соответствующая этому графу, имеет вид

(3.4)

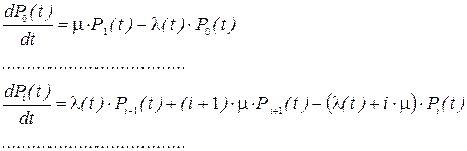
2. Если на предприятии может эксплуатироваться не более nавтомобилей моделей одной марки, то имеет место процесс гибели и размножения с ограниченным числом состояний, размеченный граф которого представлен на рис. 3.9.

Рис. 3.9. Граф состояний

Система уравнений Колмогорова для размеченного графа (рис. 3.9) имеет вид (3.4).

Эту систему надо решать при начальных условиях, рассмотренных выше. Решения систем уравнений (3.4) и (3.5) являются одномерными законами распределения Р_i(t). Отыскание решений систем в общем виде при произвольном виде функции l(t) представляет значительные трудности и не имеет практических приложении.

(3.5)

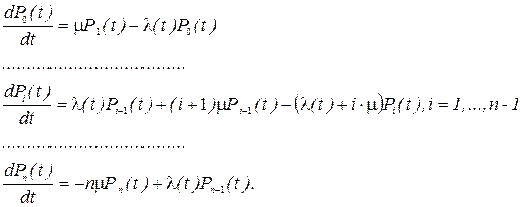
При постоянных интенсивностях потоков гибели и размножения и конечном числе состояний будет существовать стационарный режим. Система S с конечным числом состояний (n + 1), в которой протекает процесс гибели и размножения с постоянными интенсивностями потоков гибели и размножения, является простейшей эргодической системой. Размеченный граф состояний для такой системы представлен на рис. 3.9.

Предельные (финальные) вероятности состояний для простейшего эргодического процесса гибели и размножения, находящегося в стационарном режиме, определяются по следующим формулам:

(3.6)

(3.7)

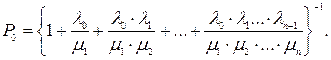
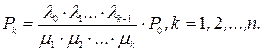
В предыдущем примере для стационарного режима если интенсивность поступления автомобилей постоянная (l(t) = l = const), то финальные вероятности состояний при условии, что нет ограничений на число автомобилей на предприятии, равны

(3.8)

. (3.9)

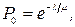
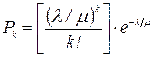
При этом математическое ожидание числа эксплуатируемых автомобилей равно его дисперсии:

Если существует ограничение по числу автомобилей на предприятии (не более n), то финальные вероятности можно записать в таком виде:

(3.11)

(3.12)

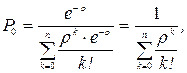
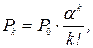
Математическое ожидание числа эксплуатируемых автомобилей в стационарном режиме

(3.13)

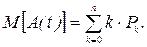
1. Построить граф состояний для системы S (четыре станка).

2. Написать дифференциальные уравнения для вероятностей состояний.

3. Найти математическое ожидание числа станков M_t, успению прошедших профилактику к моменту t.

Граф состояний показан на рис. 3.10, в котором:

S₀ – все четыре станка нуждаются в профилактическом ремонте;

S₁ – один станок успешно прошел профилактику, а три нуждаются в профилактическом ремонте;

S₂ – два станка успешно прошли профилактику, а два нуждаются в профилактическом ремонте;

S₃ – три станка успешно прошли профилактику, один нуждается в профилактическом ремонте;

S₄ – все четыре станка успешно прошли профилактику.

Рис. 3.10. Граф состояний системы

Каждый профилактический ремонт успешно заканчивается с вероятностью P, что равносильно P-преобразованию потока окончаний ремонтов, после которого он останется пуассоновским, но с интенсивностью Pl(t). В этом примере мы имеем дело с процессом чистого размножения с ограниченным числом состояний.

Уравнения Колмогорова имеют следующий вид:

Начальные условия P₀(0) = 1, P₁(0) = … = P₄(0) = 0. При постоянной интенсивности l(t) = l и вероятности состоянии определяются по следующим формулам:

Математическое ожидание числа дисков, успешно прошедших профилактику к моменту t, равно

Очевидно, что здесь процесс чистого размножения без ограничения на число состояний, при этом l_i(t) = l(t), так как интенсивность выпуска автомобилей не зависит от того, сколько их уже выпушено. Граф состояний такого процесса показан на рис. 3.11.

Рис. 3.11. Граф состояний

Одномерный закон распределения случайного процесса Х(t) для графа, изображенного на рис. 3.11, определяется следующей системой уравнений Колмогорова:

Так как число выпушенных автомобилей X(t) на любой фиксированный момент t распределено по закону Пуассона с параметром

Рассмотренный в этом примере процесс X(t) называетсянеоднородным процессом Пуассона. Если интенсивность l(t) = l = const, то получим однородный процесс Пуассона. Для такого процесса при P₀(0) = 1, P_i(0) = 0 (i > 0)

Характеристиками процесса Пуассона будут

Задача 1. Имеется прибор, который состоит из четырех узлов; поток отказов – простейший, среднее время безотказной работы каждого узла равно 11 час. Отказавший узел сразу начинает ремонтироваться; среднее время ремонта узла равно 2 час. (поток восстановления простейший). Найти среднюю производительность прибора, если при четырех работающих узлах она равна 100%, при трех 60%, при двух и менее прибор вообще не работает.

Источник