Как построить пятиугольник в изометрии
Практическая работа №5. Построение прямоугольной изометрической проекции группы геометрических тел и точек, принадлежащих поверхностям данных тел.
Изучите теоретический материал
5.1. Общие сведения. Государственный стандарт устанавливает несколько видов аксонометрических проекций. Для построения
Положение осей диметрической проекции дано на рисунке 67, б.
5.2. Аксонометрические проекции многоугольников. Построение аксонометрических проекций начинают с проведения осей. Параллельно им откладывают размеры отрезков.
Рассмотрим построение аксонометрических проекций плоских геометрических фигур, расположенных в горизонтальной плоскости. Построения даны в изометрической проекции.
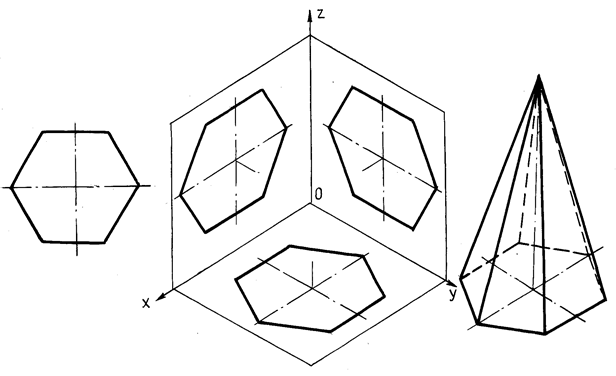
Шестиугольник. По оси х0 вправо и влево от точки 00 (рис. 70) откладывают отрезки, равные стороне шестиугольника. По оси у0 симметрично точке 00 откладывают отрезки, равные половине расстояния L между противоположными сторонами шестиугольника, т. е. L/2
Через точки, полученные на оси у0, проводят вправо и влево параллельно оси х0отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.
Если контур фигуры сложный, то при построении аксонометрической проекции эту фигуру удобно заключить в квадрат, прямоугольник и пр. (рис. 71).
Рассмотрим построение овала, представляющего изометрическую проекцию окружности. Овал удобно строить, вписывая его в ромб, который является изометрической проекцией квадрата. Построение выполняют в следующем порядке:
Строят ромб, сторона которого равна диаметру изображаемой окружности. Для этого через точку 00 проводят оси х0 и у0 (рис. 72, а). На них от точки С0откладывают отрезки С01, С02 и т. д., равные радиусу изображаемой окружности. Через точки 1, 2, 3 и 4 проводят прямые, параллельные осям х0 и у0, получая на чертеже точки A, Б, С и D.
Как начертить пятиугольник в изометрии
Соединив точки 1, 2, 3, 4, 5 прямыми линиями, получаем аксонометрическую проекцию пятиугольника.
Построение аксонометрических проекций плоской кривой сводится к построению проекций ряда ее точек и соединению их в определенной последовательности. На рис. 2 показано построение эллипса, расположенного в плоскости координатных осей X, Y.
построение аксонометрической проекции окружности
При наличии некоторого навыка для вычерчивания эллипса вполне достаточно восьми точек – рис. 5 Точки 1 и 2 – концы большой оси, 3 и 4 – концы малой оси. Точки 5, 6, 7, 8 – аксонометрические проекции концов диаметров окружности, параллельных координатным осям X, Y. Для определения большего количества точек можно применить следующий способ. На кромке полоски бумаги (рис. 5) отложить отрезки AB и AC, равны по величине соответственно большой и малой полуоси эллипса. Если точку С заставить скользить (рис. 5) вдоль большой оси эллипса, а точку B – вдоль малой оси, то точка A опишет эллипс.
В диметрии приближенное вычерчивание эллипса можно производить для окружности, расположенной в плоскости, параллельной XZ и для окружностей, расположенных в плоскостях, параллельных XY и ZY. Порядок вычерчивания показан на рис. 5.
диаграмма умножения размеров на коэффициенты искажения
На наклонных линиях диаграммы наносят значения коэффициентов, которым эти линии соответствуют.
Построение аксонометрических проекций многогранников сводится к определению аксонометрических проекций их вершин, которые затем соединяют между собой отрезками прямых линий. На рис. 72 показано построение изометрической проекции плоской фигуры шестиугольника, расположенного параллельно плоскостям проекций.
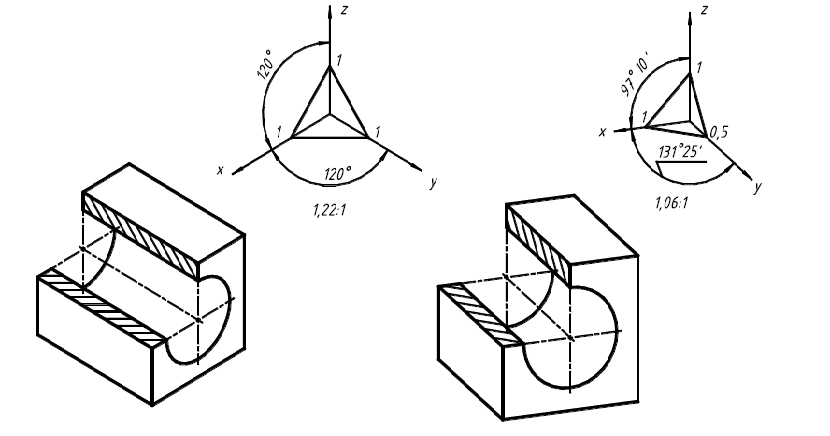
Рис. 72. Построение шестиугольника и пирамиды
в прямоугольной изометрии
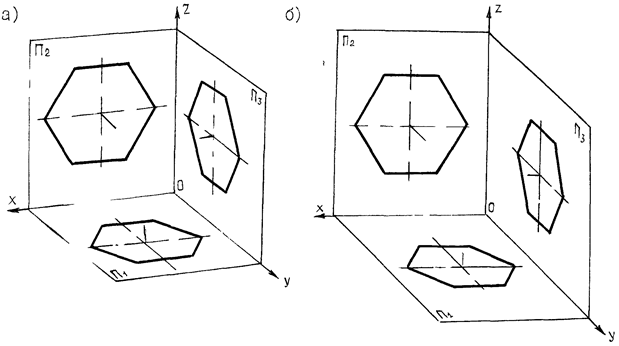
Рис. 73. Аксонометрические проекции шестиугольника:
а – прямоугольная, б – косоугольная диметрии
Рис. 74. Прямоугольная изометрическая проекция
шестигранной призмы
Прямоугольная изометрическая проекция
правильной шестигранной призмы
Построение призмы выполняют в такой последовательности. Если основание призмы – правильный многоугольник (например, шестиугольник), то построение вершин основания по координатам можно упростить, проведя одну из осей координат через центр основания. На рис. 74 оси х, у, z проведены через центры правильных шестиугольников призмы. Построим изометрию основания призмы. Из вершин шестиугольника основания проводим прямые, параллельные соответственно осям x, у или z (для каждой из рассматриваемых на рис. 74 призм). На этих прямых от вершин основания отложим высоту призмы и получим изометрию шести точек 1–6 вершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы, затем обведем видимые и невидимые линии.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8829 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
В прямоугольной изометрической проекции оси x, y, z расположены под углом 120º друг к другу. При этом ось z всегда располагается вертикально. Все коэффициенты искажения по аксонометрическим осям одинаковы и равны 0,82, поэтому размеры изображаемого объекта вдоль осей, при создании аксонометрического изображения, должны быть умножены на данный коэффициент искажения. Такая изометрия называется точной или теоретической. Для упрощения обычно применяют приведенную или практическую изометрию, выполненную в масштабе 1,22:1. При этом применяют приведенные коэффициенты искажения, которые равны единице по всем трем осям, что очень удобно при выполнении построении.
Процесс построения изометрических изображений «плоских» геомет-
рических фигур начинают с построения их исходного изображения.
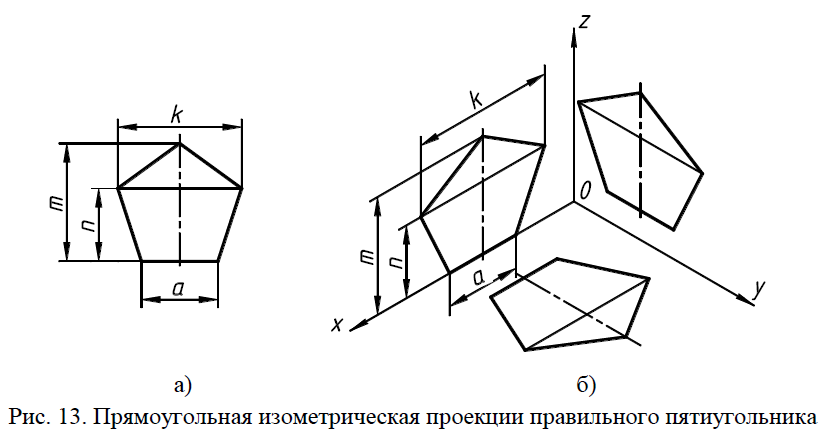
Например, для построения изометрии правильного пятиугольника сначала необходимо построить его ортогональную проекцию (рис. 20, а), на кото-
рой можно будет замерять необходимые расстояния: a, k, m, n и отклады-
вать их вдоль направления соответствующих координатных осей (рис. 20, б).
Рис. 20. Прямоугольная изометрическая проекция правильного пятиугольника
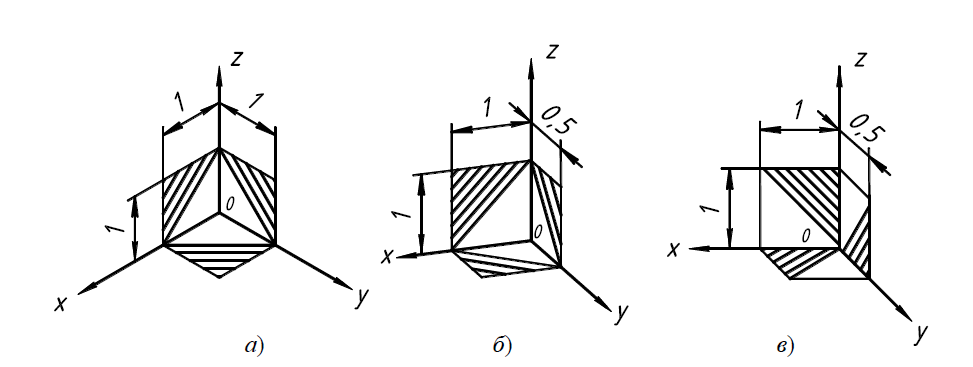
На рисунке 19, а) изображена изометрическая проекция куба с
окружностями, вписанными в его грани. Квадратные грани куба будут
изображаться в виде ромбов, а окружности – в виде эллипсов. Стоит заметить, что малая ось каждого эллипса всегда перпендикулярна его большой оси.
В зависимости от того, какой плоскости проекций принадлежит эл-
липс, его малая ось будет располагаться параллельно одной из координационных осей. Так, например, если окружность лежит в плоскости XOY,
то его малая ось будет располагаться параллельно оси z, а большая ось будет ей перпендикулярна (рис. 21, а). Аналогично, если эллипс лежит в плоскости XOZ, то малая ось параллельна оси y, а если эллипс в YOZ, то малая ось сонаправлена с осью x. При этом длина малой оси равна 0,71d, где d – диаметр изображаемой окружности, а большая ось – 1,22d (рис. 21, б).
Рис.21. Прямоуголная изометрическая проекция окружности
Построение изометрических проекций геометрических тел, в частно-
сти многогранников, сводится к определению аксонометрических проекций их вершин, которые затем соединяются между собой отрезками прямых линий.
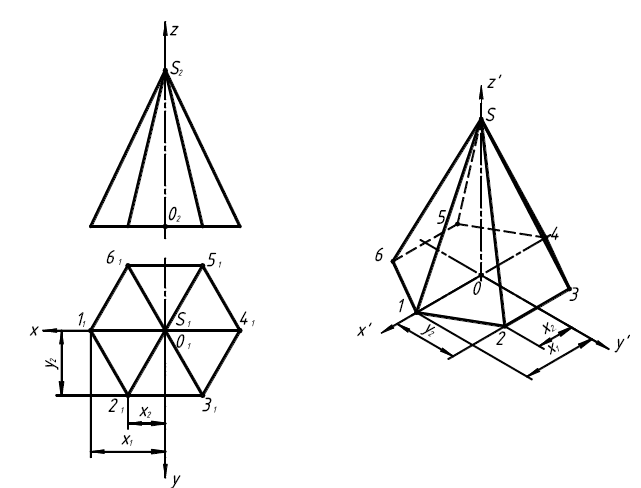
На рисунке 22 показано построение изометрического изображения правильной шестигранной пирамиды, основание которой лежит в плоскости XOY, а высота пирамиды совпадает с осью z, по ее ортогональным проекциям (рис. 22, а).
Рис. 22. Прямоугольная изометрия правильной шестиугольной пирамиды
Очень часто для повышения наглядности аксонометрического изоб-
ражения выполняются разрезы изображаемого объекта, то есть предмет изображают с удаленной некоторой ее частью (рис. 23). При этом секущие плоскости располагаются параллельно координатным плоскостям. Для обозначения материала предмета в разрезе наносят штриховку
Рис. 23. Аксонометрические проекции детали с четвертью выреза
Линии штриховки наносятся параллельно одной из диагоналей квад-
ратов, лежащих в соответствующих координатных плоскостях (рис. 24).
Рис. 24. Штриховка на аксометрических изображениях
а) в прямоугольной изометрии; б) в прямоугольной диметрии;
в) в косоугольной диметрии
Аксонометрические изображения является достаточно наглядными.
Однако перспектива наиболее реалистичнее передает видимый нами объект, так как аппарат центрального проецирования более всего соответствует аппарату человеческого глаза, но перспективные проекции являются и наиболее трудными для построения.
Как начертить пятиугольник
А так же с помощью окружности и двух лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника.
Еще один простой графический способ: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.
Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.
Точки G,E,B,F,H – вершины правильного пятиугольника.
Построение с помощью приема Биона (позволяющего построить правильный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).
Например: для n=5. Построим правильный треугольник ABC, где AB – диаметр заданной окружности. Найдем на AB точку D, по следующему соотношению: AD : AB = 2 : n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона правильного вписанного пятиугольника.
При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся меньше 10,3%.
Общий способ построения правильных многоугольников по заданной стороне по методу Ф. Коваржика (1888 г.), на основе принципа Л. да Винчи.
Единый способ построения правильного n-угольника на основании теоремы Фалеса.
Можно добавить только, что приближенные методы построения многоугольников оригинальны, просты и красивы.